连续型随机变量函数的分布教学设计

臧鸿雁， 张志刚， 李 娜

(北京科技大学 数理学院，北京 100083)

1 引 言

随着数据科学的兴起，概率论与数理统计的理论和方法越来越多地渗透到自然科学和社会科学的各个领域，成为这些领域解决实际问题的强有力工具.著名数学家拉普拉斯曾说过：“生活中绝大多数问题其实都是概率问题.”讲好概率论与数理统计课程，对提升高校人才培养质量有着十分重要的作用.各高等院校的数学工作者积极探索概率论与数理统计课程的教学改革方法和课程中知识点的教学设计[1-3].

在概率论与数理统计课程教学中，随机变量函数的分布是一个教学重点也是一个教学难点，很多数学工作者针对随机变量函数的分布知识点的教学方法进行研究[4-6].[4]利用分布函数法构造一类适用于求解一维随机变量函数分布的直观解法，该方法基于数形结合思想构建统一方法求解一维随机变量函数的分布，确定了几类适用的场合，并给出了三个典型例题的应用过程.[5]针对X，Y分别是离散、连续不同类型的随机变量的情形，如何求其函数g(X，Y)的分布的问题给出了求解方法和应用举例.[6]中探讨了一维连续型随机变量函数的分布的求法及其在产生随机数中的应用，关于随机数的讨论并未给出严格的数学证明和基于数值模拟的直观结果.

荷兰数学教育家弗莱登塔尔说：“真正的数学家，常常凭借数学的直觉思维做出各种猜想，然后加以验证.猜想验证是一种重要的数学教学方法.”本文针对一维连续型随机变量这一知识点，先提出问题，依据数值模拟直观猜测结果，再分析问题，理论证明验证结果.最后以随机数产生为目标，从理论分析到直观的数值模拟结果，对连续型随机变量函数的分布这一知识点进行了拓展研究.

2 提出问题并猜测结果

2.1 通过例子引入问题

引例同学们在毕业的时候，都会面临着找工作的问题，假设有这样一份工作，月薪方案为底薪0.4万元加提成，提成为销售额的10%，而月销售额是个随机变量X，假设其服从如下均匀分布X～U(2,4)(单位：万元)，求月薪超过7000元的概率？

首先，月薪是随机变量Y，已知X～U(2,4)，可以得到X的概率密度函数为

还有一个关键的信息是容易获得的，那就是Y和X之间的函数关系Y=0.4+0.1X.所以这个问题的关键就是求月薪Y的分布.X经过这样一个线性变换之后还会服从均匀分布吗？下面用数据做数值模拟直观观察Y的分布.

2.2 通过数值模拟猜测结果

用数据做实验看直观的结果.首先，用Matlab生成区间(2,4)上均匀分布随机数，再对这些数据进行变换，做出变换后的数据的统计直方图，如图1.图1(a)的变换函数为Y=0.4+0.1X.直观感觉，均匀分布的数据变换经过变换Y=0.4+0.1X后看起来还是均匀分布.如果改变变换函数是不是还能得到均匀分布呢？比如变换函数取对数函数, 图1(b)的变换函数为Y=lnX.由图可见，经过变换Y=lnX之后看起来不再均匀.直观的结论是否正确？能否在理论上得到这样的结果？进一步探讨理论上的解决问题的方法.

(a)Y=0.4+0.1X (b)y=lnX

3 解决问题的思路和方法

3.1 问题分析及思路

问题是如何由X的概率密度fX(x)和Y与X的函数关系获得Y的概率密度fY(y).直接建立X的概率密度和Y的概率密度之间的关系并不容易，概率密度函数与分布函数之间有关系，分布函数是由概率定义的，那是不是能从分布函数入手来间接寻找X与Y的概率密度之间的关系呢？关系的建立思路如图2所示.这就是分布函数法的思路，具体的关系的建立见下面的例子和定理1所描述.

图2 分布函数法思路图

3.2 解决问题

由前面的分析知道，可以从Y的分布函数FY(y)入手，再将Y替换为X的函数，从而转换为X落入一个区间的概率，用FX(x)表示，详细过程如下：

FY(y)=P{Y≤y}=P{0.4+0.1X≤y}=P{X≤10(y-0.4)}=FX(10(y-0.4)).

再两边对y求导，有

可见，Y～U(0.6,0.8),与前面的直观感觉是一致的，从而很容易得到月薪超过7000元的概率为1/2.问题研究到这里就可以解决引例中的问题了，但研究不满足于此，这种方法推广到一般的函数，能得到什么样的具有一般性的条件和结论呢？

4 一般性的问题描述和方法探索

很容易给出问题的一般描述，即已知X的概率密度fX(x)和Y与X的函数关系Y=g(X),求Y的概率密度fY(y).解决该问题的思路见图2，从Y的分布函数入手.

FY(y)=P{Y≤y}=P{g(X)≤y}

进一步要想从不等式中解出X的表达式，必须加条件，如果y=g(x)单调递增，则其存在反函数g-1，令g-1=h.则上式可以进一步推导

FY(y)=P{Y≤y}=P{g(X)≤y}=P{g-1(g(X))≤g-1(y)}=P{X≤h(y)}=FX(h(y)).

对上式两边对y求导，还需要补充条件，若h(y)是可导的，由复合函数求导公式，则有

fY(y)=F′Y(y)=fX(h(y))·h′(y).

这样，很容易得到下面定理1.

定理1若随机变量X的概率密度fX(x)在[a,b]外等于零，在区间[a,b]上恒有g′(x)>0，(注意：包含了前面推到所需要的两个条件y=g(x)单调递增和h(y)可导)，则有结论

有了上述的启发和推导，进一步提出问题：

(i)若y=g(x)单调递减，会得到什么样的结论？

(ii)若随机变量X的概率密度fX(x)在(-∞,+∞)上都非零，上述结论有什么变化？

(iii)若y=g(x)不单调怎么办？

以上问题让学生自己去思考和拓展即可.另外，公式法的条件比较苛刻，[7]中给出了连续型随机变量函数分布的更一般的公式法.

5 知识拓展

通过前面的分析，如果X～U(0,1)，则X的线性函数也服从均匀分布，比如Y=2X+1，则Y～U(1,3),如图3所示.

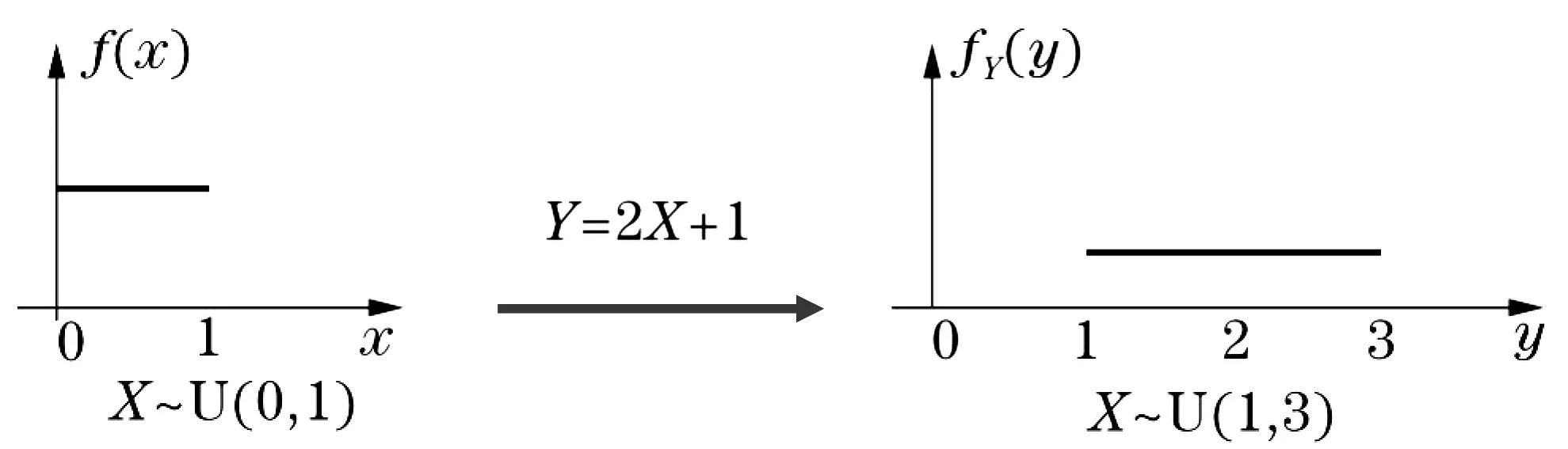
图3 均匀分布的线性函数的分布

进一步思考，如果想由均匀分布得到指数分布，能不能找到相应的变换函数呢？为了回答这个问题，给出以下定理2.

定理2如果X的分布函数为F(x),且F(x)为严格单调递增连续函数，令Y=F(X)，则Y～U(0,1).(证明略)

基于上述定理，很容易得出以下结论：

如果Y～U(0,1)，想利用Y得到其它分布的随机变量，如果想获得分布函数为F(x)的随机变量X，则只需要做变换X=F-1(Y)即可.比如，X～U(0,1)，想获得参数为1的指数分布，其分布函数和反函数分别为

由参数为1的指数分布的分布函数的反函数形式，很容易找到变换函数为Y=-ln(1-X).所以，令Y=-ln(1-X),则Y服从参数为1的指数分布.用Matlab生成[0,1]上均匀分布的随机数10000个，对这些随机数进行Y=-ln(1-X)的变换，随着数据量的增加，变换后的数据越来越接近指数分布，样本概率密度和理论概率密度越来越接近，如图4所示.数值模拟的结果，验证了理论的正确性.

图4 Y=-ln(1-X)的分布

随机数应用领域十分广泛，比如，彩票、博弈、通信、计算机仿真、计算物理学等，而以上结论为产生各种分布的随机数提供了重要的理论依据.

6 教学效果评价

关于随机变量函数的分布教学设计中，本节的问题和解决问题的方法是否掌握？随机变量的函数的分布中生成随机数的拓展是否可以理解？是否有意义？本节课的收获怎么样等问题，笔者针对北京科技大学2019级的物联网、信安、材控三个专业的160名左右的学生做了问卷调查，回收问卷145份，结果见图5.

图5 关于学生学习效果的调查问卷柱状图

由图5可见，学生对本文提出的教学设计有较高的认可度.从图5(c)的结果可以看出，尽管有些同学不能完全掌握本节的知识，但依然觉得关于随机数的拓展是十分有必要的.学生对知识拓展的需求是比较强烈的，而课堂上增加知识拓展部分能够提升知识的高阶性和挑战度.

7 结 论

本文针对概率论与数理统计课程中的连续型随机变量函数的分布这个知识点进行了教学设计，提出问题，依据数值模拟直观猜测结果，分析解决问题的思路，解决问题，推广到更一般的问题描述，探索更一般解决问题的方法，以应用为导对知识进行了拓展.最后通过对学生的调查问卷显示，本教学设计学生能够使学生较好地掌握本节知识点，学会了解决问题的方法，得到的学生认可度较高，该教学设计方法可以类似推广到其它知识点的教学设计中.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.