椭球上三维均匀分布的参数估计

张莉莉， 鲁富荣

（1．山西农业大学文理学院，山西太谷 030801；2．山西大学商务学院理学系，山西太原 030031）

0 引 言

均匀分布是概率论中的一个常用分布。目前，有关区间［a，b］上一维均匀分布的研究已有很多成果，对于二维均匀分布的研究，其成果主要有矩形区域和圆内二维均匀分布的参数估计及区域面积的估计［1－3］。文献［4－5］研究了长方体上的三维均匀分布问题，文献［6］考虑了n维球内均匀分布的参数估计问题。文中主要研究椭球上三维均匀分布的参数估计问题，并给出了未知参数与椭球体积的矩估计及参数的最大似然估计和区间估计。

1 定义及引理

定义1 设Ω是空间上的有界区域，其体积为V。若三维随机变量（X，Y，Z）有概率密度

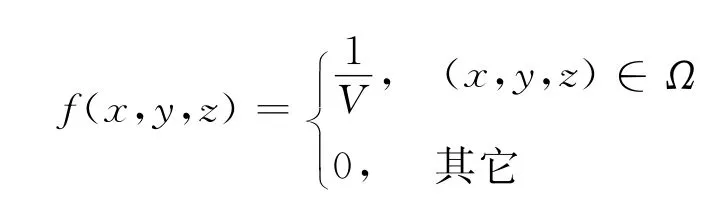
则称（X，Y，Z）在Ω上服从均匀分布。注1：当

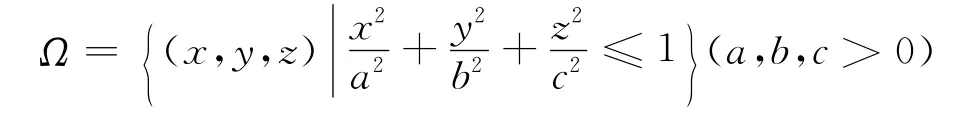
引理1 设三维随机变量（X，Y，Z）为来自球x2＋y2＋z2≤a2上均匀分布的总体，a＞0未知，（X1，Y1，Z1），（X2，Y2，Z2），…，（Xn，Yn，Zn）为其n个样本，（x1，y1，z1），（x2，y2，z2），…，（xn，yn，zn）为样本值，则球半径a的最大似然估计量为

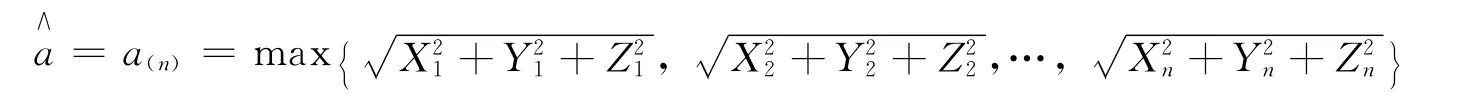
证明：随机变量（X，Y，Z）的概率密度函数为

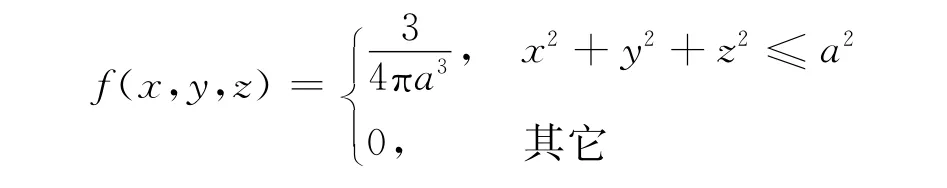
令

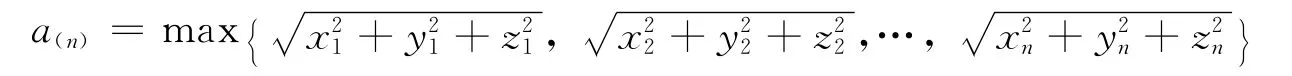
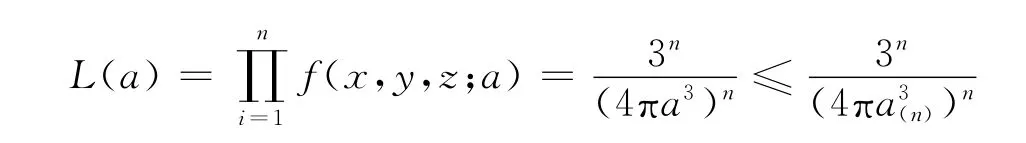
即L（a）在a＝a（n）时，取到最大值故a的最大似然估计值为

a的最大似然估计量为

注2：本引理用另一方法证明了文献［7］中n＝3的结论。

引理2［7］设随机变量（X，Y，Z）在球x2＋y2＋z2≤a2上服从均匀分布，a＞0未知，则a的置信水平1－α的置信区间为且此区间为用作为枢轴量建立的置信水平为1－α的最短置信区间，其中a∧为a的最大似然估计。

2 参数的矩估计

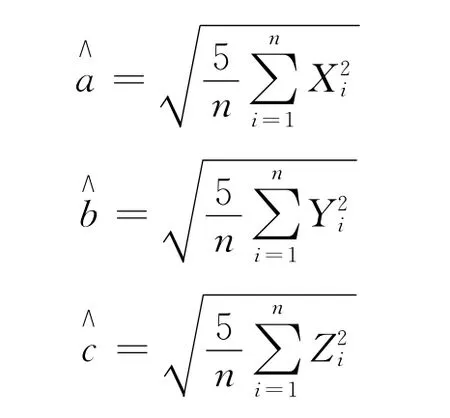
椭球体积V的矩估计量为

证明：随机变量（X，Y，Z）的概率密度函数为

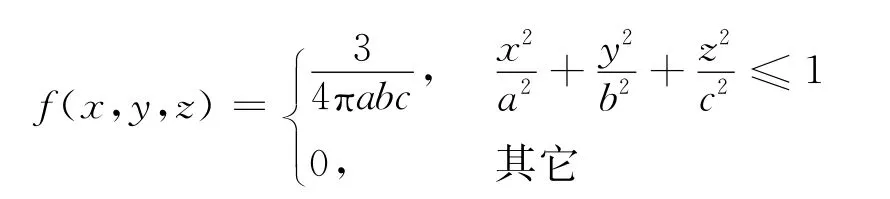
作广义球坐标变换

则X，Y，Z的2阶原点矩分别为：

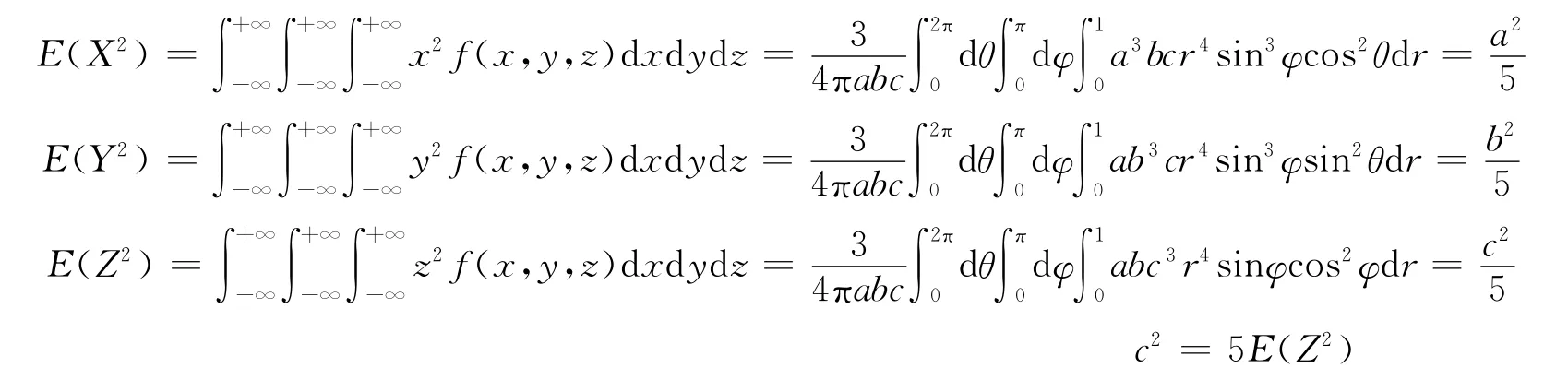
即a2＝5E（X2）b2＝5E（Y2）

X，Y，Z的6阶混合原点矩为

即

a2b2c2＝315E（X2Y2Z2）

所以，椭球半轴长a，b，c的矩估计量分别为：

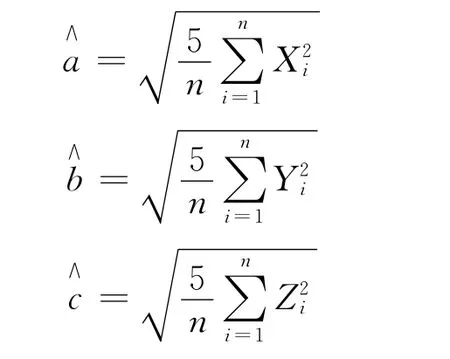
椭球体积V的矩估计量为

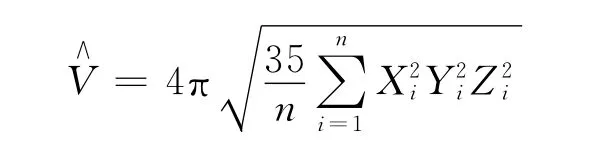
注3：当a＝b＝c时，可得服从球x2＋y2＋z2≤a2上均匀分布的三维随机变量，球体积V＝的矩估计量为

3 参数的最大似然估计

定理2 设三维随机变量（X，Y，Z）在椭球上服从均匀分布，令U＝X，，则随机变量（U，V，W）服从球u2＋v2＋w2≤a2上的均匀分布。

证明：随机变量（X，Y，Z）的概率密度函数为

作变换

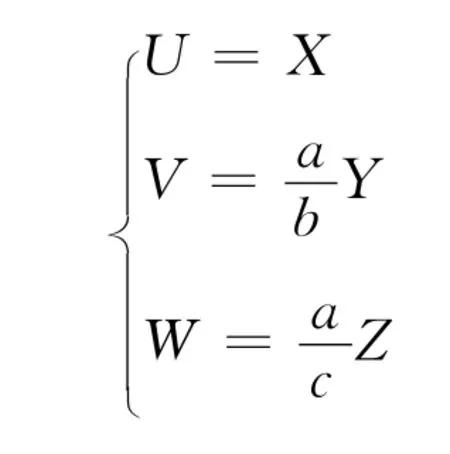
即

则三维随机变量（U，V，W）的概率密度函数为

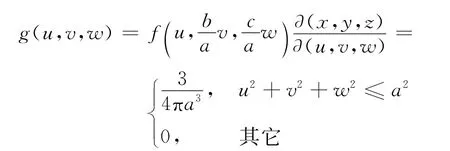
所以，三维随机变量（U，V，W）服从球u2＋v2＋w2≤a2上的均匀分布。

定理3 设三维随机变量（X，Y，Z）为来自椭球上均匀分布的总体，（X1，Y1，Z1），（X2，Y2，Z2），…，（Xn，Yn，Zn）为来自这一总体的n个样本。若椭球的半轴长之比＝k2已知，则a的最大似然估计量为

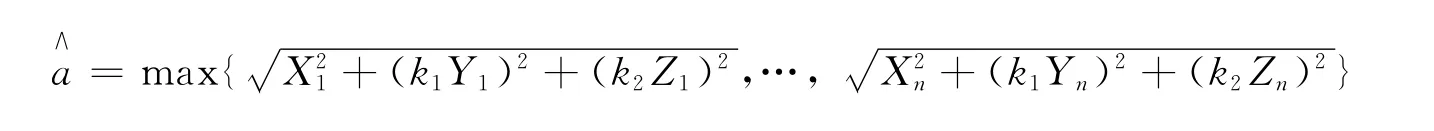
b的最大似然估计量为

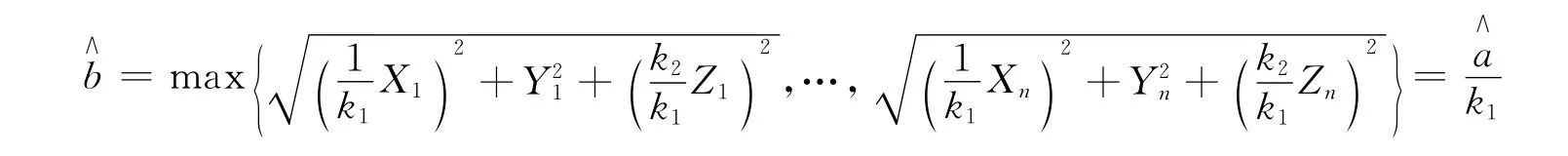
c的最大似然估计量为

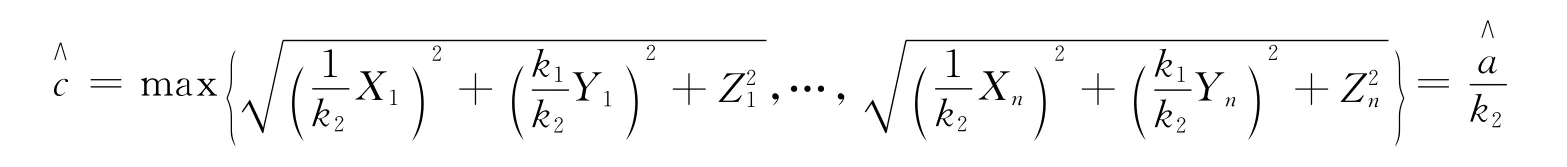
证明：由引理1和定理2证之。

4 参数的区间估计

定理4 设三维随机变量（X，Y，Z）在椭球上服从均匀分布，若椭球的半轴长之比已知，则a，b，c的置信水平为1－α的置信区间分别为且这些区间分别为用作为枢轴量建立的置信水平为1－α的最短置信区间。其中分别为a，b，c的最大似然估计。

证明：由引理2和定理3易证之。

综上所述，我们得到了椭球上三维均匀分布未知参数及椭球体积的矩估计，在椭球半轴长之比k1，k2已知的条件下，还得到了参数的最大似然估计和区间估计。当这个比值未知时，可先求出k1，k2的矩估计量，然后得参数的两步估计［7］。另外，文中结论不难推广到n维椭球上均匀分布的情况。

参数估计问题是统计推断的一类基本问题，除点估计与区间估计以外，还可研究参数的Bayes估计，如文献［8］讨论了Poission分布、二项分布、几何分布的Bayes估计，对于均匀分布参数的Bayes估计有待进一步考虑。

［1］ 鲁富荣，张莉莉．椭圆上二维均匀分布的参数估计［J］．山西大同大学学报，2010，26（4）：6－8．

［2］ 刘兆君．二维均匀分布矩形区域面积的估计［J］．大学数学，2007，23（4）：155－159．

［3］ 王志祥．圆内二维均匀分布的参数估计［J］．大学数学，2008，24（2）：150－152．

［4］ 刘兆君，吕永敬．三维均匀分布长方体域边长的联合置信域［J］．山东师范大学学报，2007，22（4）：132－133．

［5］ 陈光曙．长方体上均匀分布的密度函数［J］．纯粹数学与应用数学，2009，25（4）：721－724．

［6］ 王志祥．n维球内均匀分布的参数估计［J］．纯粹数学与应用数学，2009，25（4）：789－793．

［7］ 王松桂，史建红，尹素菊，等．线性模型引论［M］．北京：科学出版社，2004：5．

［8］ 邢蕾，赵鹏飞．Q－对称熵损失函数下几何分布参数估计［J］．长春工业大学学报：自然科学版，2008，29（6）：614－616．