基于最小二乘法的PC连续刚构桥挠度关键影响参数优化

卢海峨, 张 军

(内蒙古路桥集团有限责任公司， 内蒙古 呼和浩特 010051)

0 引言

在桥梁施工控制过程中，受施工条件和环境因素影响，连续刚构桥结构的实际形变、应力与有限元模型的理论计算值存在着较大误差。若仅依据有限元模型的理论计算值对桥梁施工进行指导，那么结构的实际形变与应力分布会逐渐偏离理想的成桥状态，因此,在连续刚构桥施工控制中需要通过优化参数对有限元模型进行调整，以减小结构实测值与理论计算值之间的误差。由于结构应力的测量受环境与人为因素影响较大，所得应力结果误差也较大，不适宜作为参数优化的目标。本文以影响结构挠度关键参数作为优化目标，基于最小二乘法对结构挠度关键影响参数进行优化[1]，使工程实测值与有限元模型理论计算值误差减小到了1 mm以内，优化效果良好，可为类似工程提供借鉴。

1 基于最小二乘法的参数优化方法

最小二乘法是一种数值分析方法，经常应用于数学模型的建立与各类桥梁施工控制过程中。该方法应用于有限元模型参数修正时的计算方法如下。

假定采用悬臂浇筑的主梁结构处于第N个施工阶段，则主梁各控制点挠度实测值为：

{DR}m=[DR(1)，DR(2)，…，DR(m)]T

(1)

式中：m为主梁挠度控制点选取的个数，其数值要求必须大于挠度影响参数的个数；DR(k)(k=1，2，…，m)是第k个梁段控制点的挠度。

在此施工阶段下，主梁控制点的理论挠度值为：

{DT}m=[DT(1)，DT(2)，…，DT(m)]T

(2)

则该控制点挠度理论值与实测值之间的误差为：

{ΔD}m={DR}m-{DT}m

(3)

设此时有限元模型中挠度影响参数理论值组成的向量为：

{PT}m=[PT(1)，PT(2)，…，PT(m)]T

(4)

而此时桥梁结构中挠度影响参数实测值组成的向量为：

{PR}m=[PR(1)，PR(2)，…，PR(m)]T

(5)

式中：PT(k)(k=1，2，…，m)和PR(k)(k=1，2，…，m)分别是第k个挠度影响参数的理论值和实测值。

挠度影响参数的理论值与实际值误差是：

{ΔP}m={PR}m-{PT}m

(6)

在有限元模型中计算该施工阶段挠度影响参数PT(k)改变一定比例的数值时，第k个梁段挠度DT(k)相应变化αij，则可得出挠度影响参数对主梁结构变形的影响矩阵[A]mn。

由挠度影响参数误差{ΔP}n导致的控制点挠度误差是{Δd}m：

{Δd}m=[A]mn{ΔP}n

(7)

残差为：

ε={ΔD}m-{Δd}m={ΔD}m-

[A]mn{ΔP}n

(8)

相对残差平方和是：

J=εTε=({ΔD}m-[A]mn{ΔP}n)T·

({ΔD}m-[A]mn{ΔP}n)

(9)

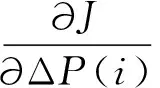
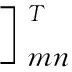
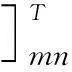
(10)

再用求解出的计算误差修正有限元模型中的结构参数，即完成了此施工阶段的参数优化。

2 工程概况

以湖南某特大跨径PC连续刚构桥为例，该桥上部结构为预应力混凝土连续刚构，桥跨组合为(91+168+91)m。主梁为单箱单室箱型截面，顶板宽13.5 m，底板宽7.0 m；箱梁墩顶到跨中的梁高与底板厚度均呈1.8次抛物线变化，梁高从9.5 m减小至3.2 m，底板厚度从1.0 m减小至0.3 m。

边跨及跨中合龙段长2 m，两边跨现浇段长5.6 m。该桥桥墩为箱形独柱空心墩，主梁使用C55混凝土，桥墩采用C50混凝土。桥型布置见图1。

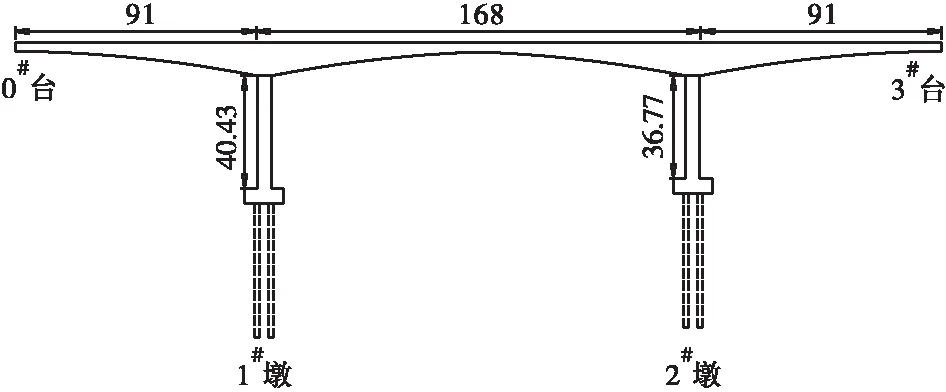
图1 连续刚构桥桥型布置(单位： m)

采用Midas/Civil建立该桥有限元模型，依据设计图纸模拟桥梁施工阶段。全桥采用空间梁单元模拟，墩底采用固结约束，桥墩与主梁之间采用弹性连接中的刚性连接，单T悬臂浇筑共分为20个节段，每个节段等分为19段，即得20个挠度控制点，有限元模型共50个施工阶段，有限元模型见图2。

图2 有限元模型示意

3 挠度影响参数的敏感性分析

连续刚构桥的施工工期长，影响其结构挠度的因素较多。为了减少不必要的计算，应先对各参数进行敏感性分析，以筛选出影响桥梁结构形变的关键参数，并对其进行优化。经查阅相关资料[2]，连续刚构桥主梁下挠的影响参数及其作用机理见图3。

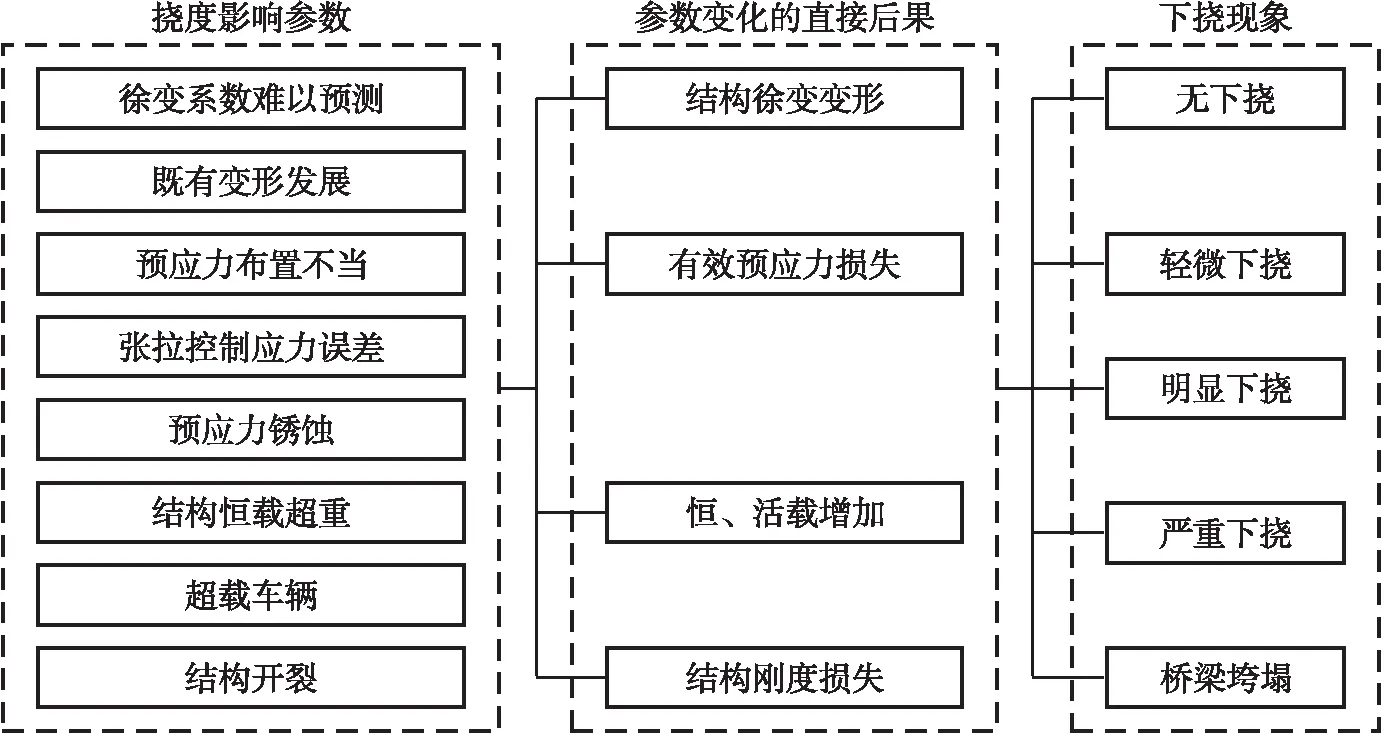
图3 连续刚构桥下挠影响参数的作用机理

由图3可得连续刚构桥结构下挠影响的几种基本参数，据此可计算该桥2#墩的18#块当前施工阶段挠度及18#块施工阶段累计挠度相应的各影响参数敏感性系数，并取绝对值进行对比分析，选取的参数理论值和变化范围如表1所示。

依据相应规范、文献[3～8]以及该桥所处地理环境对各参数进行了取值，取值方法说明如下：

1)该桥所处环境相对湿度变化范围为55%～85%，原模型环境相对湿度为70%，因此,分别取环境相对湿度为55%、65%、75%和85%进行计算。

2)预应力参数包括张拉控制应力、管道摩擦系数以及管道偏差系数。其中，张拉控制应力通过钢束的伸长量进行校对，规范允许的实际伸长值误差应保持在设计值±6%之内，因此,分别取张拉控制应力变化-6%、-3%、3%和6%进行计算；管道摩擦系数规范[8]规定的取值范围为[0.15，0.20]，原模型的取值为0.17，因此,分别取管道摩擦系数为0.15、0.16、0.19、0.20进行计算；该桥采用预埋塑料波纹管，根据规范[8]，其局部偏差系数均值为0.0015，依据相关文献[4]，分别取管道偏差系数为0.000 9、0.001 2、0.001 8和0.002 1进行计算。

表1 敏感性分析的参数项目徐变参数预应力参数预应力参数预应力参数刚度参数自重参数环境相对湿度/%张拉控制应力管道摩擦系数管道偏差系数弹性模量混凝土容重参数理论值701 395 MPa0.170.001 5 m-13.55×107 kN/m225 kN/m3参数变化范围±21.4±6%-11.8%～17.7%±40%±20%±10%

3)该桥主梁使用C55混凝土，原模型中按其弹性模量均值取3.55×107 kN/m2，根据相关文献[7]，取原模型中弹性模量数值的-20%、-10%、10%、20%分别进行计算。

4)该桥有限元模型的混凝土容重均值取25 kN/m3，参考相关规范[8]，分别取混凝土容重为22.5、23.75、26.25、27.5 kN/m3进行敏感性参数计算。

各参数敏感性系数计算结果见表2、表3(为简化篇幅，仅汇总偶数号控制点的计算结果)。

由表2、表3可知，弹性模量对于悬臂阶段的主梁挠度影响极小，基本可忽略不计，因此,对比结果时予以忽略，其余5个参数的敏感性系数绝对值见图4和图5。

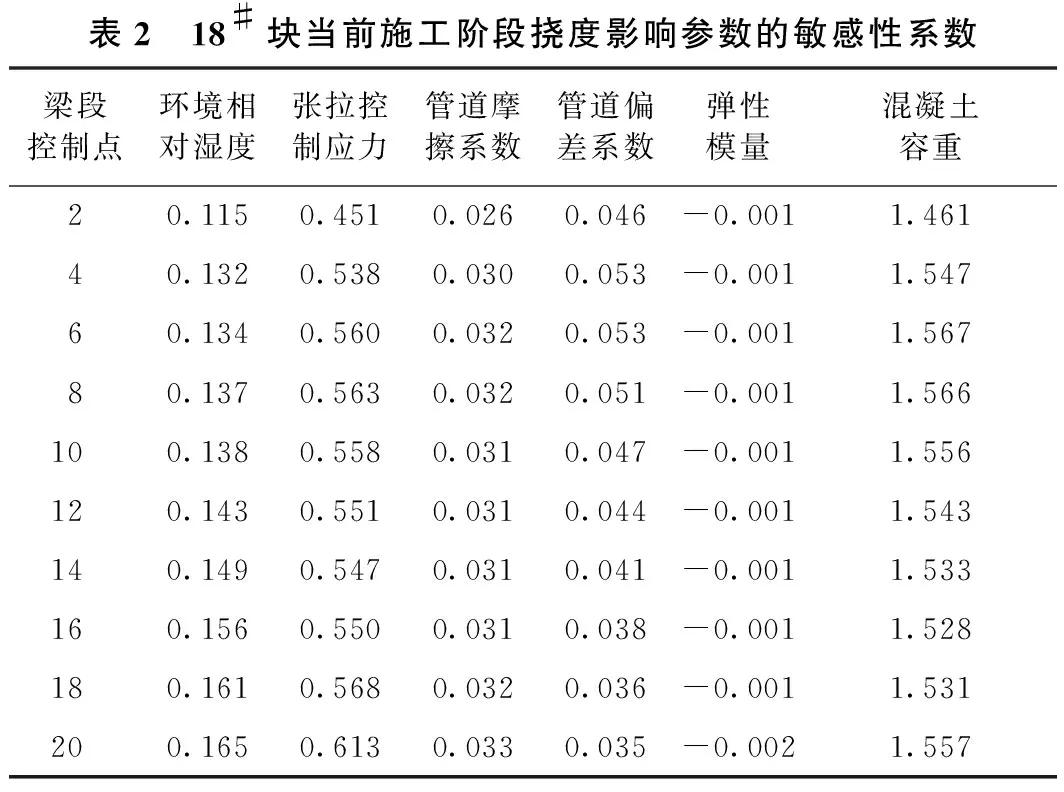
表2 18#块当前施工阶段挠度影响参数的敏感性系数梁段控制点环境相对湿度张拉控制应力管道摩擦系数管道偏差系数弹性模量混凝土容重20.115 0.451 0.026 0.046 -0.0011.461 40.132 0.538 0.030 0.053 -0.0011.547 60.134 0.560 0.032 0.053 -0.0011.567 80.137 0.563 0.032 0.051 -0.0011.566 100.138 0.558 0.031 0.047 -0.0011.556 120.143 0.551 0.031 0.044 -0.0011.543 140.149 0.547 0.031 0.041 -0.0011.533 160.156 0.550 0.031 0.038 -0.0011.528 180.161 0.568 0.032 0.036 -0.0011.531200.165 0.613 0.033 0.035 -0.0021.557

表3 18#块施工阶段累计挠度影响参数的敏感性系数梁段控制点环境相对湿度张拉控制应力管道摩擦系数管道偏差系数弹性模量混凝土容重20.016 0.898 0.045 0.047 -0.0011.49040.021 1.563 0.082 0.085 -0.0012.09460.035 1.934 0.101 0.107 -0.0012.473 80.052 2.025 0.104 0.114 -0.0012.597 100.067 1.948 0.100 0.111 -0.0012.551120.086 1.708 0.093 0.100 -0.0012.389 140.087 1.331 0.070 0.080 -0.0012.051 160.109 1.073 0.057 0.063 -0.0011.779180.122 0.811 0.044 0.047 -0.0011.539 200.165 0.613 0.033 0.035 -0.0021.557

由图4、图5可知，影响该桥施工阶段挠度的最关键参数为混凝土容重与张拉控制应力，环境相对湿度、管道摩擦系数与管道偏差系数对主梁悬臂浇筑施工阶段的挠度影响较小，属于结构形变的次要影响因素。因此，在桥梁施工控制过程中，应对混凝土容重与张拉控制应力这2种挠度影响的关键参数进行优化。

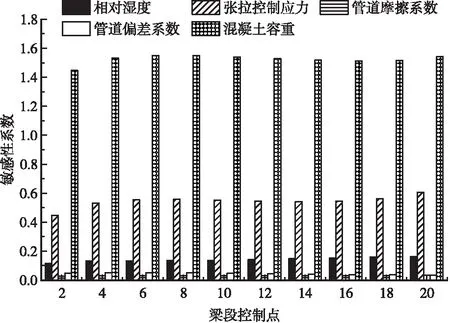
图4 18#块当前施工阶段挠度的敏感性对比

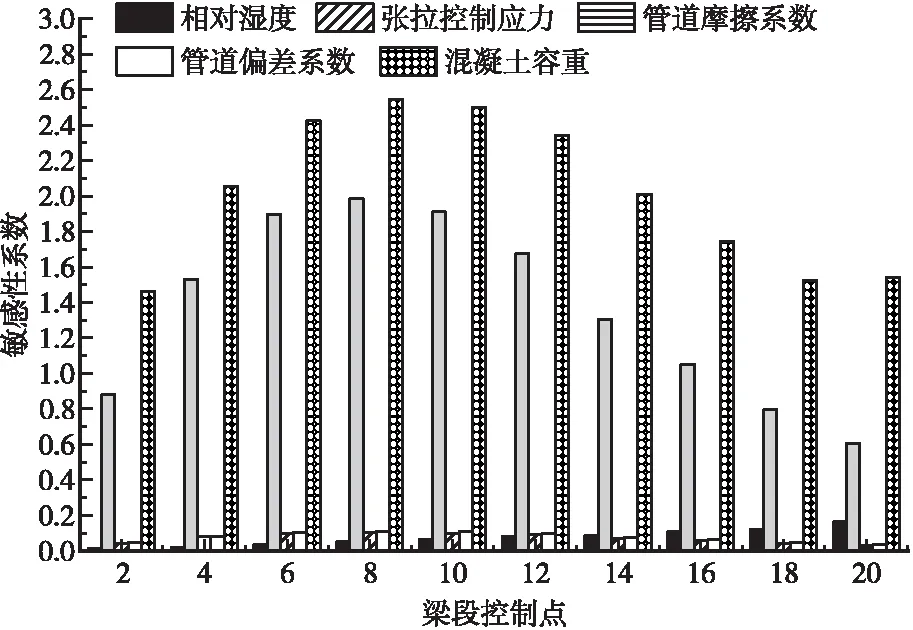
图5 18#块施工阶段累计挠度的敏感性对比

4 参数优化过程及结果对比

当主梁悬臂长度较短时，结构挠度较小，而测量值又易受到测量误差影响，此时不宜进行参数优化。随着悬臂长度增加，结构挠度对其影响参数的敏感性增加，测量误差与结构施工阶段挠度的比值不断减小，此时参数优化效果更为明显，因此，本文选择该桥18#梁段靠近悬臂端的6个控制点进行优化。

根据挠度影响因素的敏感性对比分析结果，选取混凝土容重和张拉控制应力作为结构的挠度关键影响参数，采用基于最小二乘法参数优化方法，对2#墩中跨18#梁段靠近悬臂端6个控制点的挠度关键影响参数进行优化，优化过程如下：

原有限元模型中，18#梁段的混凝土容重和张拉控制应力数据如表4所示。

表4 18#梁段参数理论值挠度影响参数混凝土容重/(kN·m-3)张拉控制应力/MPa初始值251 395

18#梁段自浇筑到预应力张拉后，主梁控制点挠度的理论值与实测值见表5。

由表5可知，控制点挠度的误差向量为：

(11)

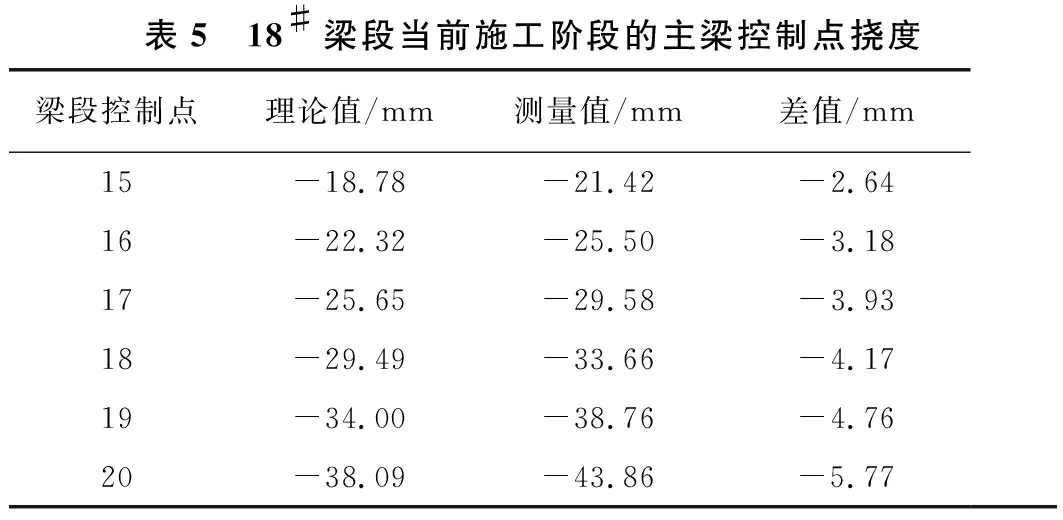
表5 18#梁段当前施工阶段的主梁控制点挠度梁段控制点理论值/mm测量值/mm差值/mm15-18.78-21.42-2.64 16-22.32-25.50-3.18 17-25.65-29.58-3.93 18-29.49-33.66-4.17 19-34.00-38.76-4.76 20-38.09-43.86 -5.77

挠度影响参数相对误差组成的向量为：

{Δδ}2=[Δδ(1) Δδ(2)]T

(12)

式中：Δδ(1)为混凝土容重误差与其理论值的比值；Δδ(2)为张拉控制应力误差与其理论值的比值。

由挠度影响参数的敏感性系数计算结果可知，当张拉控制应力变化±6%以内、混凝土容重变化±10%以内时，主梁结构的变形与参数的数值基本呈线性相关。在有限元模型中依次改变混凝土容重和张拉控制应力参数数值，并对计算结果进行分析，可以得到这2个参数在18#梁段当前施工阶段中相对于靠近悬臂端6个控制点挠度的影响矩阵[A]mn：

(13)

由挠度影响参数的相对误差{Δδ}2导致的控制点挠度误差{ΔD}6，满足：

{ΔD}m=[A]mn{Δδ}n

(14)

[A]mn只有两列，存在广义逆，则{Δδ}2的最小二乘解为：

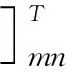
{0.079 -0.050}

(15)

使用该参数相对误差调整原模型中18#梁段的混凝土容重和张拉控制应力数值，调整后的参数值及18#梁段当前施工阶段主梁控制点挠度见表6。

表6 18#梁段调整后的参数值设计参数混凝土容重/(kN·m-3)张拉控制应力/MPa修正值27.4641 353.178

18#梁段的参数调整后，有限元模型计算得到的梁段控制点挠度见表7。

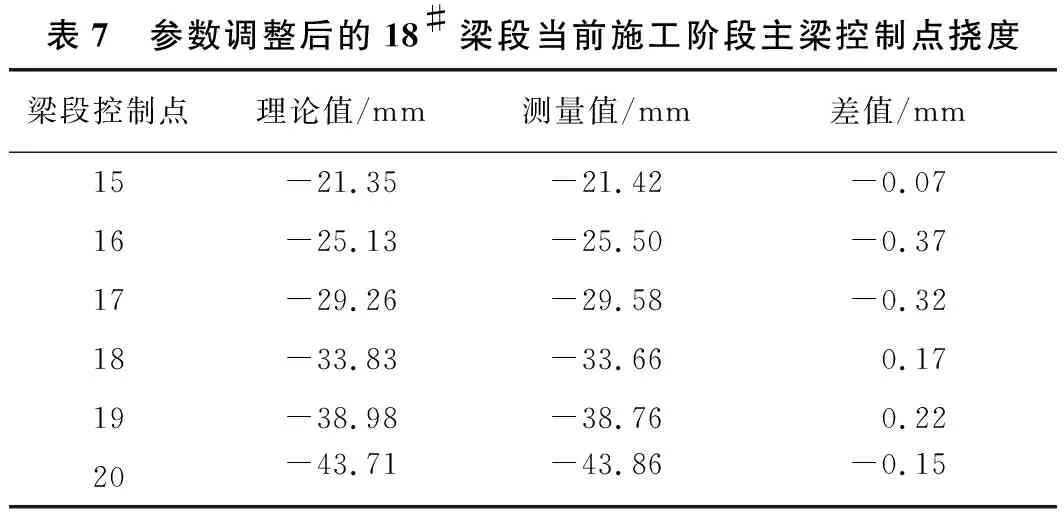
表7 参数调整后的18#梁段当前施工阶段主梁控制点挠度梁段控制点理论值/mm测量值/mm差值/mm15-21.35-21.42 -0.0716-25.13-25.50 -0.3717-29.26-29.58 -0.3218-33.83-33.66 0.1719-38.98-38.76 0.2220-43.71-43.86 -0.15

对比分析表5、表7可知，有限元模型参数优化前各控制点挠度计算值与工程实测值之间的误差差值在为2.64～5.77 mm，优化后的误差差值均小于1 mm，说明模型参数的优化效果较明显。

5 结论

以某特大跨径PC连续刚构桥为工程背景，采用Midas/Civil建立该桥空间有限元模型，计算分析了影响该桥施工阶段挠度的最关键参数，并基于最小二乘法对关键影响参数进行优化，对比优化前后有限元模型计算值与实测值的差值，可得到以下结论：

1)通过对比计算挠度影响参数，分析出了影响PC连续刚构桥施工阶段挠度最关键的参数为混凝土容重与张拉控制应力，而环境相对湿度、管道摩擦系数与管道偏差系数对主梁悬臂浇筑施工阶段的挠度影响较小，属于影响结构形变的次要参数。

2)基于最小二乘法优化了18#梁段混凝土容重和张拉控制应力参数值，对比优化前后18#梁段6个控制点的挠度理论值与测量值的差值可得，有限元模型参数优化前各控制点挠度计算值与工程实测值之间的差值在2.64～5.77 mm之间，优化后的差值均小于1 mm，表明参数优化效果较好，计算结果验证了基于最小二乘法的参数优化方法的优越性。