基于拉力场理论的腹板连接剪切型可替换耗能梁段的极限承载力分析

殷占忠 徐少波 冯大哲 杨 博

(1兰州理工大学土木工程学院, 兰州 730050)(2兰州理工大学西部土木工程防灾减灾教育部工程研究中心, 兰州 730050)

偏心支撑框架具有中心支撑框架结构刚度大和纯钢框架结构延性好的优点,抗震性能良好[1-5].耗能梁段作为偏心支撑钢框架的主要耗能元件,令Mp、Vp分别为耗能梁段塑性抗弯承载力和抗剪承载力，a为耗能梁段长度,根据长度比ξ=a/(Mp/Vp),将耗能梁段主要分为剪切屈服型、剪切弯曲型和弯曲屈服型.传统的偏心支撑框架体系将耗能梁段和框架梁设计为整体,难以评估震后结构受损程度,耗能梁段修复替换的成本也大幅提高.为此,国内外学者将耗能梁段与框架梁分离设计成可替换耗能梁段.Mehmet等[6]给出了可替换耗能梁段的设计建议,并通过试验验证了其抗震性能的优异性.纪晓东等[7]对4种不同连接方式的耗能梁段进行试验,发现采用端板-抗剪键作为连接形式的耗能梁段可拆装性更好.殷占忠等[8-9]通过试验验证了端板连接可替换耗能梁具有良好的耗能能力和可替换性,但端板连接的可替换耗能梁段容易在端板与梁段连接的焊缝处发生脆性破坏,导致该耗能梁段提前失效.然而,相关研究主要针对端板连接形式可替换耗能梁段的力学和抗震性能,针对腹板连接剪切型可替换耗能梁段的研究还较少.

近年来工字形钢梁的受力破坏机理和极限承载力计算是研究热点之一.目前,考虑屈曲后强度的计算理论主要有拉力场理论和旋转应力场2种.前者包括假定拉力带在加劲肋之间产生的Basler拉力场理论[10]和假定拉力带在翼缘间产生的Rockey拉力场理论[11], 后者在计算极限承载力时需考虑翼缘刚度的影响.Höglund[12]提出了旋转应力场理论,采用该理论计算极限承载力时无需考虑拉力带作用,只需考虑翼缘和腹板的作用,由此得到的计算结果相较于拉力场理论计算结果更加保守,与真实情况误差较大.康孝先等[13]结合数值模拟与试验得到的嵌固系数对拉力场理论进行了修正,修正后的理论计算结果与试验结果及数值模拟结果相符.段兰等[14]根据试验得到的高强度工字形钢梁腹板剪切破坏机理,建立了考虑翼缘约束效应的计算公式,计算结果与试验结果吻合较好.李立峰等[15]通过试验和数值模拟发现对于发生弹性剪切屈曲的钢板梁,考虑屈曲后强度进行理论计算的精度更高,并针对不产生腹板弹性剪切屈曲的钢板梁提出了扩展拉力场理论.关于工字形钢梁受剪破坏机理及抗剪承载力的研究主要集中在传统的工字形钢梁上,对于腹板连接剪切型可替换耗能梁段的受剪破坏机理及抗剪承载力的研究鲜见报道,国内外设计规范中也未提及其计算方法.

鉴于此,本文基于拉力场理论,推导出考虑翼缘刚度影响的腹板连接剪切型可替换耗能梁段的抗剪极限承载力计算公式.根据可替换耗能梁段的截面尺寸、长度和加劲肋布置的变化,建立了14个耗能梁段有限元模型,进行数值模拟分析.结合既有试验,将数值模拟结果、试验结果与理论公式计算结果进行对比,验证腹板连接剪切型可替换耗能梁段抗剪承载力理论计算的可靠性,为简化计算耗能梁段的极限承载力提供参考.

1 可替换耗能梁段极限承载力公式

结合数值模拟与既有试验结果[16],腹板连接剪切型可替换耗能梁段在剪切荷载作用下腹板发生错动变形,翼缘变化明显,加劲肋没有变化,受力特点符合Rockey拉力场理论.当耗能梁段长度a≥322 mm时,变形主要出现在两边螺栓处.耗能梁段左右两端简支约束,上下两端固支约束.

采用Rockey拉力场理论对耗能梁段的腹板极限承载力进行推导.假定如下：① 令α为腹板连接剪切型可替换耗能梁段在剪力作用下翼缘的弯曲角度,假定tanα=α;② 假定材料弹性变形相较于塑性变形基本忽略不计,采用理想刚塑性模型,不考虑材料弹性变形、强化和软化效应;③ 极限状态下可替换耗能梁段的应力满足Mises屈服准则;④ 腹板屈曲后阶段承载力的增加由薄膜力形成的拉力场承担;⑤ 忽略加劲肋对承载能力的影响.

根据薄腹梁屈曲后强度的计算理论[17],腹板连接剪切型可替换耗能梁段在剪力作用下达到极限承载力的过程可分为如下3个阶段：① 屈曲前阶段,剪应力达到临界值τcr;② 屈曲后阶段,梁腹板薄膜力产生拉力场,拉力场中的主拉应力随着框架梁传递给耗能梁段的荷载增加而不断增大;③ 破坏阶段,在荷载作用下有拉力场的部分腹板先达到屈服,翼缘处形成塑性铰而破坏.耗能梁段两端承受框架梁传递的剪力等于耗能梁段屈曲前阶段达到临界的极限剪力与耗能梁段屈曲后阶段因薄膜力形成拉力场增加的剪力之和,故腹板连接剪切型可替换耗能梁段抗剪极限承载力可表示为

式中,Vcr为耗能梁段屈曲前阶段达到临界值时的极限剪力值;Vy为框架梁传递给耗能梁段的剪力在屈曲后阶段的增量,与梁腹板薄膜力产生的拉力场有关.

根据规范ANSI/AISC 360—2010,耗能梁段屈曲前阶段达到临界值时的极限剪力Vcr为

Vcr=τcrhotw

(1)

式中,ho为腹板高度;tw为双C槽钢腹板的总厚度.

(2)

式中,θ为薄膜拉应力与翼缘形成的夹角.

整理式(2)可得

(3)

耗能梁段翼缘处荷载不断增加,形成塑性铰.上下翼缘4个塑性铰不断发展,并在之间产生拉力带而破坏,承载力达到峰值.破坏阶段的计算模型示意图见图1.图中,c为翼缘2个塑性铰间的距离,上下翼缘相同;α为变形后边ED′与ED的夹角;δ为假定向上的虚位移;a为腹板连接剪切型可替换耗能梁段的长度;d为边HF的长度;b、tf分别为

(a) 计算模型

双C槽钢翼缘的总宽度和厚度.

根据假定板CDF没有任何变形,并给定向上的虚位移δ,即

δ=ctanα=cα

(4)

框架梁传递给耗能梁段的剪力在屈曲后阶段增加的值做功为总的虚外功Wo,即

Wo=Vycα

(5)

(6)

(7)

虚内功由4个塑性铰转动产生,即

(8)

体系的总虚内功Wi为

(9)

根据虚功原理Wo=Wi,框架梁传递给耗能梁段的剪力在屈曲后阶段的增量Vy为

(10)

腹板连接剪切型可替换耗能梁段的抗剪极限承载力为

(11)

根据Rockey拉力场理论,两铰之间的长度为

(12)

根据有限元模型可得

恒成立,故21.12°<θ<68.88°.

图2给出了抗剪承载力随角度变化曲线.由图可知,随着θ的增加,抗剪承载力不断变小.θ最小时,则抗剪承载力最大.

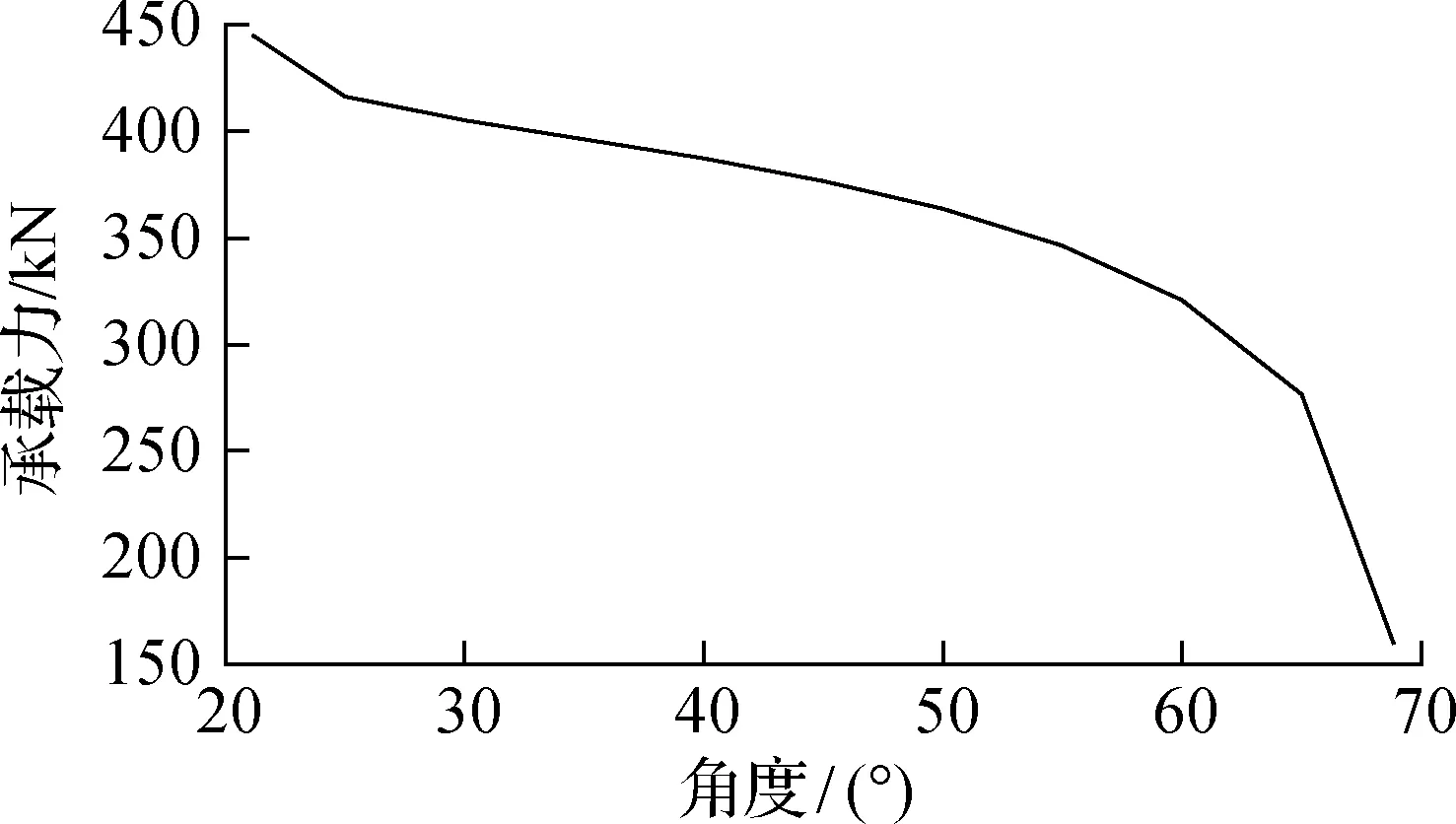
图2 抗剪承载力随角度变化曲线

2 数值模拟

2.1 几何参数

选取层高3.6 m的K形偏心支撑钢框架高层建筑底层中的一榀框架作为研究对象.框架梁、框架柱均采用H形钢,支撑为圆钢管,整体结构均采用Q235B钢材.梁柱节点采用栓焊混合连接,支撑与框架梁、柱的连接方式均为铰接,耗能梁段与框架梁通过腹板打孔锚固螺栓连接.

采用ABAQUS软件建立考虑耗能梁段截面尺寸、长度比以及加劲肋布置3种因素的腹板连接剪切型可替换耗能梁段有限元模型.以长度比ξ=a/(Mp/Vp)作为依据,确定腹板连接剪切型可替换耗能梁段有限元模型试件参数,结果见表1.试件示意图见图3.

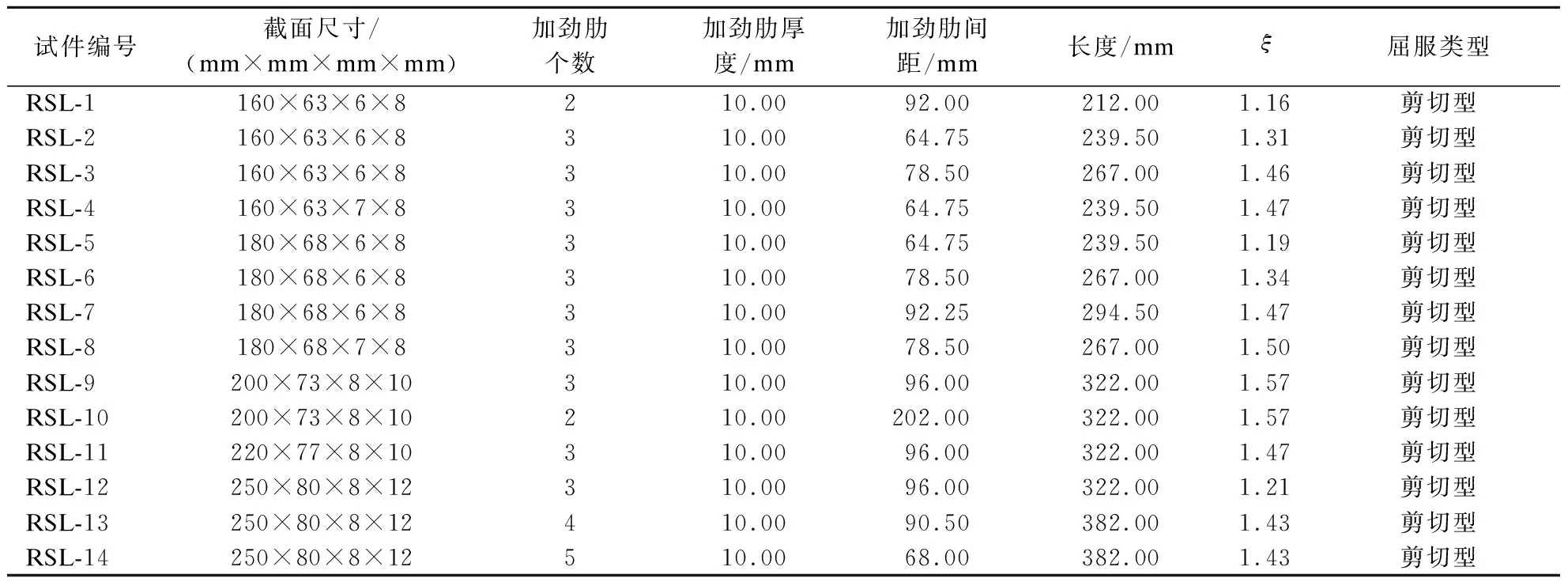
表1 试件参数

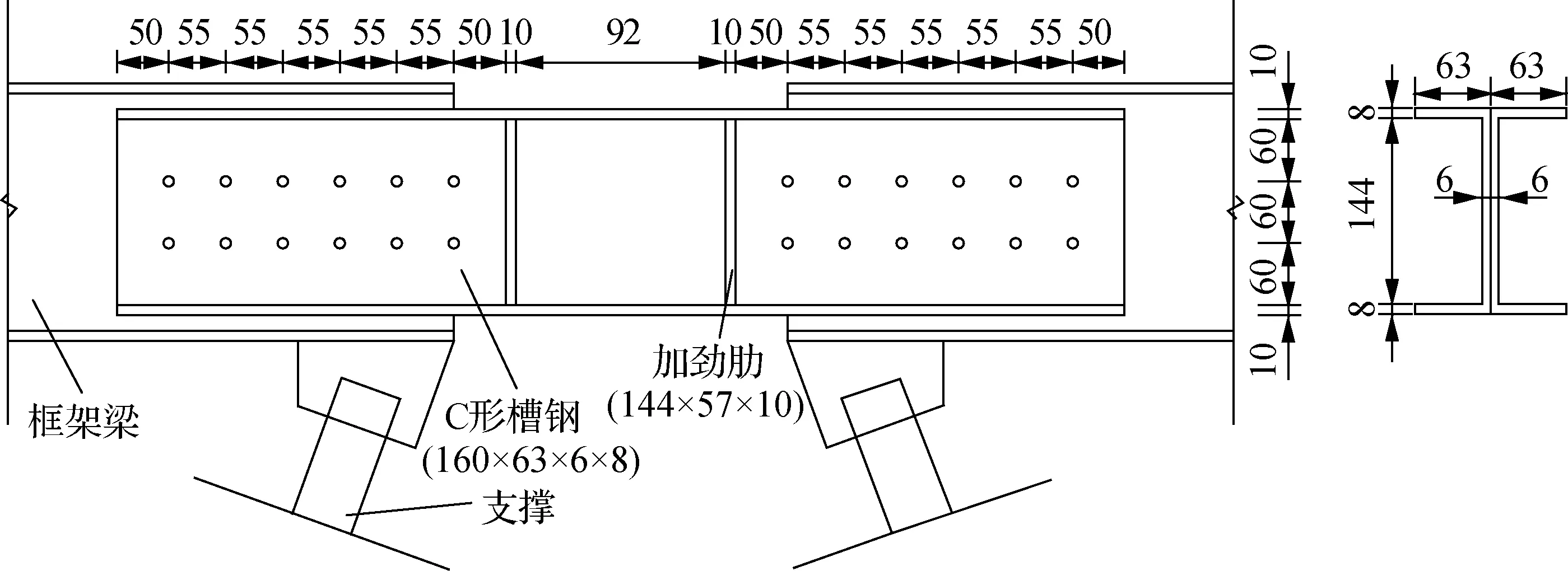
图3 试件示意图(单位：mm)

2.2 有限元模型

有限元模型中,可替换耗能梁段本构模型采用双折线模型,钢材选用Q235B,其余构件均采用理想弹塑性模型.加载装置采用Q345B钢材,高强螺栓型号为10.9级,单元类型均选用C3D8R.钢材的性能指标通过材性试验得到,结果见表2.

表2 材料性能指标

加载梁和框架梁、槽钢和加劲肋均采用TIE绑定约束,耗能梁段与加载梁、螺栓与耗能梁段以及框架梁通过Surface-to-surface约束.上下加载梁都进行位移约束以模拟铰支座,采用位移加载方式,上侧加载梁Y向位移不进行约束.有限元模型以及网格划分见图4.通过数值模拟,得到腹板连接剪切型可替换耗能梁段的力学性能,结果见表3.

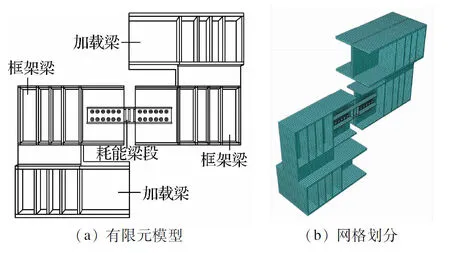
图4 有限元模型及网格划分示意图

表3 各试件力学性能

3 试验结果与对比分析

根据既有试验[16],选取RSL-1、RSL-9、RSL-10、RSL-11四个试件进行分析.以试件RSL-1为例,其加载装置示意图见图5.

图5 试验加载装置示意图

试验加载初期,试件处于弹性阶段,无明显变形.位移加载至5.7 mm时,试件进入弹塑性阶段,槽钢的翼缘部分开始轻微弯曲,伴有螺栓受力的声响,翼缘外侧漆皮鼓起(见图6(a)).位移加载至16.00 mm时,两侧加劲肋区格内腹板漆皮鼓起,开始变形,但加劲肋未发生任何变化(见图6(b)).随着位移的进一步增加,翼缘变形更加明显,腹板漆皮剥落区域进一步扩大,荷载不再随位移增大而增加,试验停止.

图6 试验照片

将数值模拟结果、试验结果以及理论计算结果进行对比,结果见表4.由表可知,基于Rockey拉力场理论推导的腹板连接剪切型可替换耗能梁段的极限承载力公式计算结果与数值模拟结果的误差值为0.09%～10.20%,与试验结果的误差值为3.9%～7.3%,均小于10%,说明该理论计算公式与数值模拟和试验吻合度较好,基于Rockey理论进行公式推导是合理的.

表4 试件试验结果、数值模拟结果及理论公式结果对比

与数值模拟和试验结果相比,理论公式计算得到的试件RSL-9～试件RSL-14的极限承载力误差较大.究其原因在于,耗能梁段长度大于322 mm,截面高度与翼缘宽度比大于2.7,较长的耗能梁段在加载后期容易发生弯曲屈曲,翼缘不能给腹板提供锚固,腹板发生屈服而不能形成拉力带,薄膜拉力做的虚内功几乎为零.因此,截面高度与翼缘宽度比大于2.7时,理论公式不考虑腹板拉力带对极限承载力的贡献.

在腹板连接剪切型可替换耗能梁段截面尺寸和加劲肋个数相同的情况下,当长度比ξ增大时,耗能梁段受力逐渐趋向受弯破坏,耗能梁段拉力带形成过程减缓,极限承载力逐渐下降,最大降幅可达9.4%.

腹板连接剪切型可替换耗能梁段长度和加劲肋布置相同时,抗剪极限承载力随双C槽钢截面高度与翼缘宽度的比值增大而提高.当高宽比为2.5～2.7时,翼缘宽度较大,对耗能梁段腹板具有较强的锚固作用,抗剪极限承载力提高较大,数值模拟得到的抗剪极限承载力提高范围为9.0%～10.8%,理论公式计算的极限承载力增大范围为14.5%～15.0%.当高宽比超过2.7时,数值模拟中翼缘伸出较短,对耗能梁段锚固作用较弱,得到的抗剪极限承载力提高范围较小,仅约3.0%,理论公式计算中仍然考虑翼缘的刚度影响,计算得到的抗剪极限承载力提高范围较大,约为11.0%.由此说明,截面尺寸对耗能梁段抗剪极限承载力影响显著.在理论计算过程中,当腹板连接剪切型可替换耗能梁段截面高度h≤200 mm,ξ≤1.50时,腹板屈曲后因薄膜力形成的拉力场而增加的承载力约占可替换耗能梁段总抗剪极限承载力的20%,最高可达23%,对抗剪极限承载力具有显著影响.当截面高度h≤200 mm,ξ>1.50或h>200 mm,ξ≥1.21时,整个腹板都发生屈服而未屈曲,抗剪极限承载力与屈曲前阶段达到临界的极限剪力基本相当,不再考虑拉力场增加的抗剪承载能力.

图7给出了试件RSL-1、RSL-9、RSL-10、RSL-11的荷载-位移曲线对比.由图可知,各试件的荷载-位移曲线趋势基本相同,均存在弹性段、屈服段和强化段,且各试件的屈服台阶明显.

图7 荷载-位移曲线对比

图8给出了试件RSL-1的变形情况.由图8(a)和(b)可知,腹板连接剪切型可替换耗能梁段最靠近加劲肋的一排螺栓孔附近翼缘存在明显的弯曲现象,圆形螺栓孔呈现出不规则形状,数值模拟与试验结果相似,破坏现象吻合.由图8(c)可知,可替换耗能梁段与框架梁连接位置处翼缘弯曲变形明显,加劲肋没有出现变形,与Rockey理论假定条件相符,说明基于Rockey理论进行公式推导是可行的.

图8 试件RSL-1变形图

4 结论

1) 腹板连接剪切型可替换耗能梁段整个发展过程分为弹性段、屈服段和强化段.基于Rockey拉力场理论推导出腹板连接剪切型可替换耗能梁段的抗剪极限承载力公式,计算结果与数值模拟结果和试验结果的误差均较小,吻合较好.

2) 当腹板连接剪切型可替换耗能梁段长度和加劲肋布置相同时,抗剪极限承载力随双C槽钢腹板高度与翼缘宽度的比值增大而提高.高宽比为2.5～2.7时,随着高宽比的增大,抗剪极限承载力明显增大,极限承载力模拟值增幅和计算值增幅分别可达10.8%和15.0%,截面尺寸对耗能梁段极限承载力影响显著,翼缘对耗能梁段腹板具有较强的锚固作用.

3) 当腹板连接剪切型可替换耗能梁段截面尺寸和加劲肋个数相同时,抗剪极限承载力随着长度比ξ的增大而降低,说明耗能梁段受力逐渐趋向受弯为主,腹板拉力带的形成受到影响.