基于CFD与POD的煤粉锅炉三维速度场快速预测
李天宇 陈 曦 钟文琪
(东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)
我国目前的一次能源结构仍然以煤为主,国内煤炭发电量在2020年较2019年增长了2%,2020年我国燃煤电力占世界燃煤电力的1/2以上[1],因此一定时期内火力发电仍然会在我国的电力结构中占据主要地位[2].火力发电厂燃煤锅炉的稳定运行对于确保供电安全具有重要意义[3],对燃煤锅炉气固流动进行优化组织可以防止锅炉受热面关键部件的磨损,延长部件寿命,避免计划外停机,提高锅炉的稳定性和能效,减少经济损失.优化气固流场防止受热面磨损的关键是实时掌握炉内速度场信息[4],但高温高尘环境和大尺寸测量对象使得传统测量方法难以获得炉内流场信息[5].在计算机技术和气固流动相关理论研究迅速发展的当下,利用数值模拟解决实际工程中的多相流动问题已在各类工程领域得到了广泛应用,其中采用计算流体力学(computational fluid dynamics, CFD)方法实现大型电站锅炉设计优化已经成为较为常用的方法[6-8],但受制于CFD复杂模型冗长的计算耗时,采用CFD难以参与锅炉实时优化控制.此外,由于锅炉内部燃烧的复杂强耦合、高度非线性和大时滞特性[9],现有的求解方法难以保证良好的实时性[10],且数值模拟方法多针对单工况点定值状态下的高可信度高精度计算,在实时调节运行等领域的应用具有一定的局限性.因此,为了减少获得流场信息所需要的计算耗时,在保证计算精度的前提下,使用降阶模型(reduced order modeling, ROM)方法将流场系统的复杂全阶CFD模型通过远小于原流场系统阶数的降阶模型进行替代成为分析处理高维流场数据的主要途径.其中,基于本征正交分解(proper orthogonal decomposition, POD)进行数据特征提取在流场信息处理和分析方面得到了广泛应用,王烨等[11]采用POD方法对管翅式换热器的流动和传热性能进行了研究,寇家庆等[12]将POD方法应用于飞行器的跨声速抖振现象的流场分析和重构;Stabile等[13]将POD方法用于研究圆柱绕流问题并建立了基于POD的低维模型.而针对锅炉燃烧系统建立POD模型对锅炉速度场进行流场分析的研究较少.因此,对锅炉速度流场构建降阶快速预测模型,实现变工况条件下锅炉速度流场信息的预测具有重要意义.
本文以一台330 MW四角切圆煤粉锅炉为研究对象,通过少数已知工况状态下全阶CFD模型计算得出的结果,利用降阶模型的数据处理手段得到流场系统的主要模态,实现以少量的模态结合模态系数组合描述出流场系统主要的动力学特征,以较低的计算成本保持模型的保真度和可信度[14].提出了一种结合计算流体力学与机器学习的方法,通过对比不同类型的机器学习模型在解决多工况参数与模态系数拟合问题时的性能,选取拟合效果最优的机器学习模型实现工况参数与模态系数之间的映射.开发了一种煤粉锅炉速度场快速预测模型,大幅缩减了获取流场信息所需的计算时间成本,同时保证了模型的计算精度,以期通过快速计算实现锅炉速度场的近实时性预测,将得到的锅炉流场信息提供给运行人员,以指导调控锅炉燃烧.
1 研究对象
1.1 数值模型建立
本文的研究对象为某电厂在役SG-1025/18.55-M727型号的330 MW亚临界自然循环四角切圆燃煤锅炉,如图1所示.燃烧器区域进风口采用四角对称分布,包括交叉布置的一次风进口5层(A、B、C、D、E)、二次风进口6层(AA、AB、BC、CD、DE、EE)以及位于最高层二次风进口上方的分离燃尽风(separated over-fire air, SOFA)进口4层(SOFA1、SOFA2、SOFA3、SOFA4).
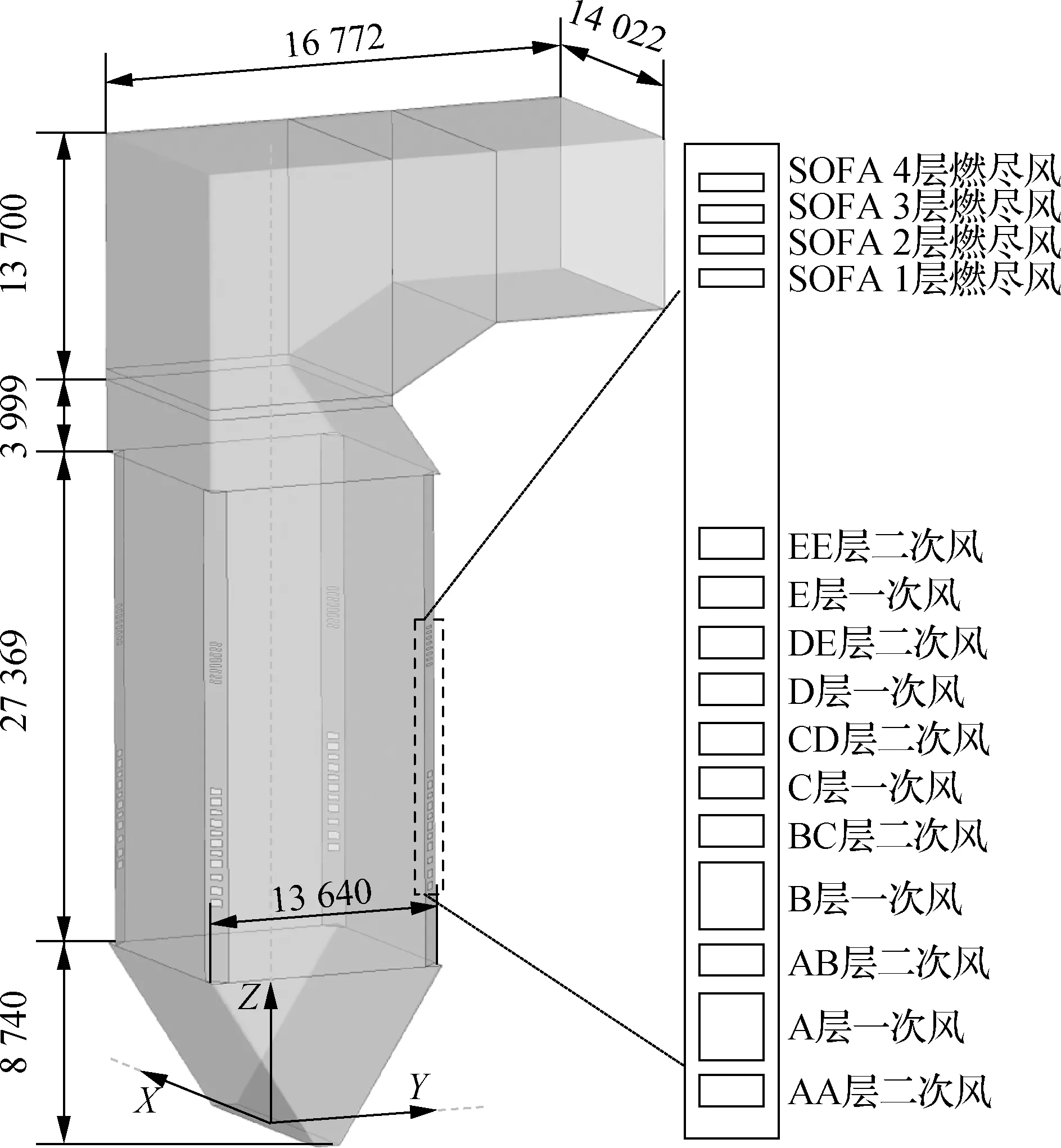
图1 锅炉结构与燃烧器区域布置(单位: mm)
采用六面体结构化网格对锅炉流场区域进行网格模型划分.针对燃烧器附近复杂流场区域和燃烧集中区域增加网格密度,网格无关性验证如图2所示.由图可知,不同网格密度与模型计算温度值相关性较小,从而验证了模拟结果与网格无关,故本文最终选取网格数量为2.14×106.数值模型选用方面,辐射传热采用P-1辐射模型,气相湍流流动采用带旋流修正的可实现k-ε双方程模型,颗粒运动采用DPM模型,焦炭燃烧采用多表面反应模型.详细设置参考文献[15-17].
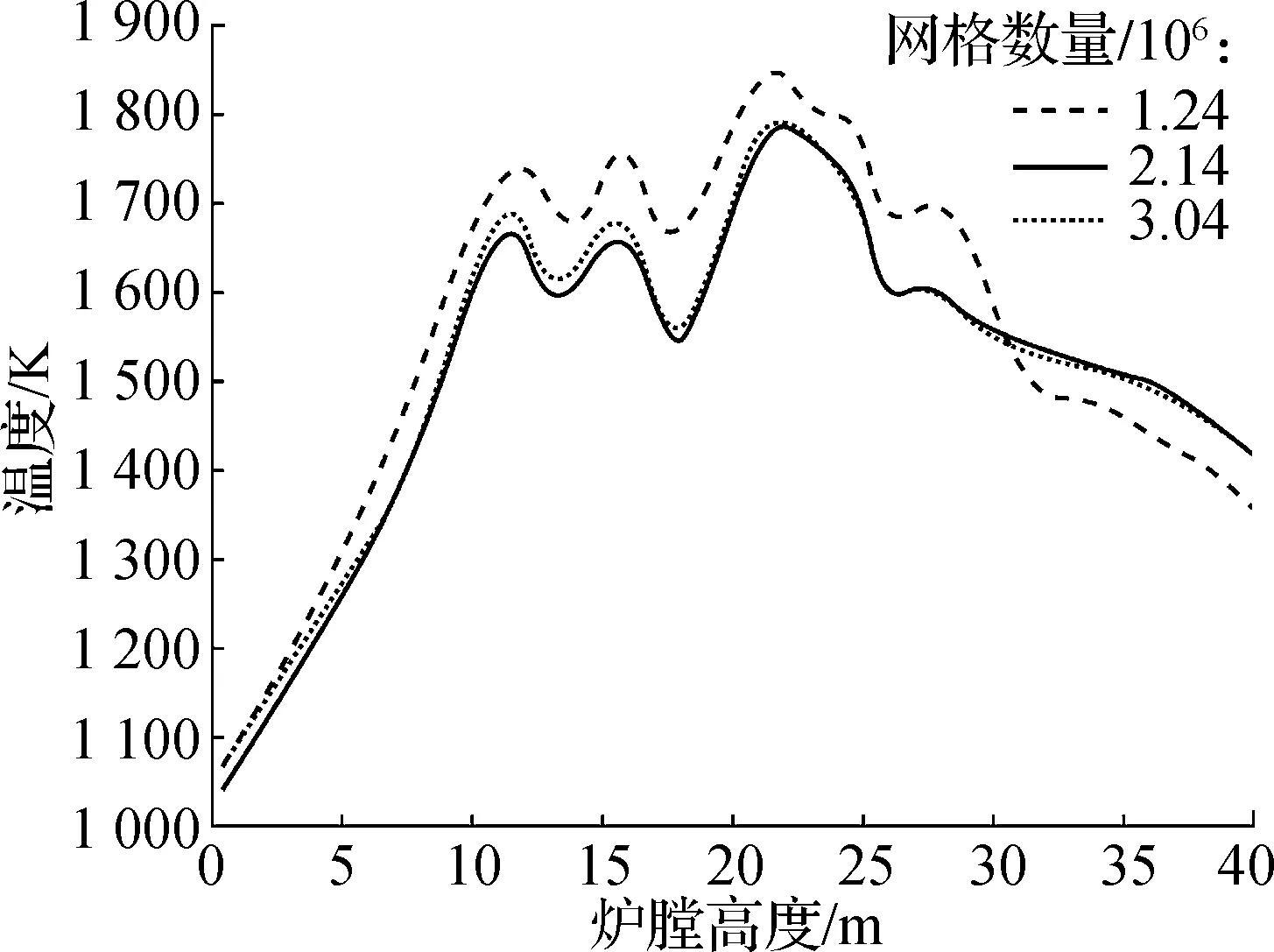
图2 网格无关性验证
通过上述建立的数值模拟模型针对目标锅炉进行不同工况负荷条件下的模拟计算,以获取原始数据集.
1.2 数值模型验证
通过比对所建立目标锅炉的数值模型计算结果数据与实际锅炉运行测量数据,对数值模型的准确性进行验证.数值模拟计算工况参数以及实际锅炉运行工况参数均选取负荷为320 MW下的典型工况参数,如表1所示.模拟结果与实际运行结果误差在5%以内,满足所需精度要求.
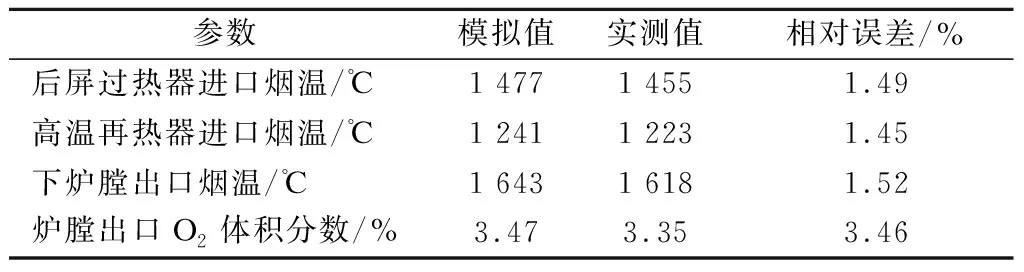
表1 目标锅炉典型工况模拟值与实测值
1.3 数据采集
针对锅炉运行参数的负荷值、各层燃烧器所用的不同煤种类别、各层燃烧器煤量、各层燃烧器风速、各层燃烧器风量、总风量、总煤量、一次风量、一次风率、二次风量、二次风率、燃尽风率等39个锅炉运行参数的不同组合,设置了585组计算工况,各参数设置标准见表2.其中,煤种类别定义根据煤的灰分Aar及热值Qar,net大小划分为优质煤、一般煤、劣质煤3种类型[17],在表2中分别对应数值1、2和3,3种煤的特性参数如表3所示.
表2 锅炉运行参数
参数数值锅炉负荷/MW165,198,231,264,297,330A层煤种1B层煤种1,2C层煤种1,2,3D层煤种1,2,3E层煤种1,2,3A,B,C,D,E层煤量/(t·h-1)0~41A,B,C,D,E层风速/(m·s-1)0~26A,B,C,D,E层风量/(m3·h-1)0~97AA,AB,BC,CD,DE,EE层风速/(m·s-1)0~67SOFA1,SOFA2,SOFA3,SOFA4开度/%0~63一次风量/(m3·h-1)15~87二次风量/(m3·h-1)47~198一次风率/%0.335二次风率/%0.420燃尽风率/%0.245过量空气系数1.25,1.3总风量/(m3·h-1)614~1 302总煤量/(t·h-1)68~176

表3 煤种类别
2 研究对象
2.1 本征正交分解模型数学原理
POD来源于矢量数据统计分析,在数据降维和流场分析等领域应用广泛.使用POD方法针对湍流以及流动传热等问题开展研究已成为学术领域较为公认的方法,如Berkooz等[18]使用POD方法进行了湍流拟序结构分析;丁鹏等[19]将POD方法运用于流动传热物理场问题的求解.利用本征正交分解方法旨在以计算流体力学软件生成的大量已知计算结果数据为基础,提取出代表流场计算结果数据主要特征的一系列最优化的基向量模态,并利用这部分模态主成分来表征原始数据,将原本高维度的复杂高阶系统替代为由主成分模态拟合表征出的低维系统,极大地降低计算代价,从而达到降维的目的,是通过降维来寻找数据内部特性、提升特征表达能力的一种基本方法.利用本征正交分解技术建立的降阶模型使得通过计算机得到近乎实时的处理结果成为可能,模型基于数据集建立的特性使非线性的流场系统通过生成的各阶模态得到较好表征的同时具有足够的精度,从而更高效地重构和预测流场分布情况.
POD模型的建立步骤如下[20-21].
① 构建样本数据集snapshot矩阵.样本数据集矩阵通过第1节建立的锅炉模型CFD数值模拟计算结果来构建.本文所研究的锅炉模型数值计算采用结构化网格,锅炉速度场系统数据集矩阵是一个大小为L×N的数值矩阵{V},其中L为矩阵行数,表示模型网格编号数;N为矩阵列数,表示锅炉运行参数工况编号数.
② 求解矩阵基函数模态与模态系数.速度场系统可以通过如下所示的相互成正交关系的基函数组合的线性叠加来表征:
(1)
式中,n表示所考虑的工况样本个数,n=1, 2,…,N;tn表示若干因变量;f(x,tn)表示速度场系统;k=1,2,…,N;αk(tn)表示第k个模态系数;φk(x)表示第k个基函数模态.
POD过程旨在从数值矩阵{V}中提取最能够准确描述f(x,tn)的一组正交的基函数,即提取出一组含能量最大并且满足最小二乘意义的POD基函数模态,等价于最大化f(x,tn)在基函数模态φk(x)上的投影,以数学方式表示即
maxφ〈(f,φ)2〉 s.t.(φ,φ)=1
(2)
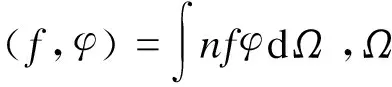
通过拉格朗日乘数法解析式(2)并进一步推导得出
(3)
式(3)为满足式(2)成立的充分条件.
特征基函数为snapshot的线性组合:
(4)
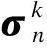
(5)
式中,δij为克罗内克尔符号;i=1,2, …,N;j=1,2, …,N.将式(4)代入式(3)得到
Aσ(n)=λnσ(n)
(6)
式中,A表示N维对称半正定矩阵;σ(n)为矩阵A的特征向量;λn为矩阵A的特征值.矩阵A的各元素Aij表示为
(7)
问题简化为求解矩阵A的特征向量σ(n).
模态系数与特征值λi的关系可表示为
〈αi(t)αj(t)〉=δijλi
(8)
③ 速度场重构.与基函数模态φk(x)相对应的特征值λk的大小表征了该基函数模态所捕获的系统能量大小,亦即该基函数模态对整个系统动力学特征的贡献度大小.因此,基函数模态的含能大小可以通过λk的大小体现.
以f(x,tn)表示流体速度,则流体系统平均动能可表示为
(9)
由式(5)、式(8)和式(9)可得,流场系统的平均动能E也可表示为所有特征值的和,即
(10)
为方便将基函数模态对流场系统总能量的贡献程度以数值量进行表达,定义参数的能量贡献率ξi和累积能量贡献率ηM如下:
(11)
(12)
式中,M≪N;ξi表示第i个基函数模态的能量贡献率;ηM表示前M个基函数模态的累积能量贡献率.
将求解得到的基函数模态按照其所含能量大小降序排列,通常前M(M≪N)组基函数模态便占据了整个流场系统绝大部分的能量,至此,可以通过较高的精度表示为如下形式:
(13)
2.2 模态重构模型建立
通过计算流体力学软件对预先设置的各不同工况参数组合进行计算,得到设置工况下锅炉内部流场的速度场分布,将各工况参数对应计算结果中的速度场数据导出,共计2 168 262个网格的速度大小数据,将已预计算的所有工况参数计算结果合并建立为一个大小为2 168 282×585的锅炉速度场原始数据数值矩阵{V},用于本征正交分解模型的构建.
POD模型经过数据处理得到流场系统速度值数据集矩阵的模态系数集合α及其对应的基函数模态集合Φ:
(14)
Φ=[φ1,φ2,…,φ584]
(15)
其中,各阶模态所含的能量大小如图3所示,第一阶模态所含能量大小的数量级远高于其他阶模态,占据了流场系统大部分的能量,随着阶数编号的增加,模态所含能量大小急剧降低并逐渐趋于稳定.
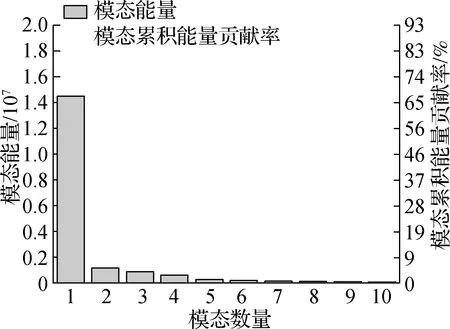
图3 模态能量与模态累积能量贡献率
随着模态数量的增加,模态累积能量贡献率的大小增加逐渐趋缓,在模态数量达到18个时模态累积能量达到了流场系统总能量的90%,继续引入更多的模态数量对模态累积能量贡献率的大小增加影响较为微小,若使累积能量达到流场系统总能量的99%则需取模态数量为187个.综合考虑模态含能与模态数量,选取前18阶基函数模态进行对研究目标流场系统的速度分布进行特征提取及重构.
取锅炉负荷330 MW下的一组工况参数组合(见表4),对该工况参数下目标锅炉燃烧器A层一次风区域(锅炉高度14.6 m处)的速度分布模态重构模型计算结果与数值模拟计算结果进行对比,如图4所示,其中数值模拟结果为通过CFD数值计算得到的速度分布,模态重构结果为通过POD前18阶模态重构得到的速度分布.由图4对比结果可以看出,含能最高的前几阶模态包含了流场系统的绝大部分本质信息,能够以较高的精度重构样本结果数据集.

表4 工况参数详值
3 模态系数拟合模型训练
将通过本征正交分解模型从流场系统数据集中提取出的模态以其对应的模态系数大小进行加权并叠加,即可实现对流场速度分布的重构;同样,将输入工况参数与各阶模态对应的模态系数之间的映射关系建立拟合模型,通过得到未知工况参数所对应的模态系数,即可实现对未知工况的预测重构.
本节以工况组合作为模型样本数据集,共计585组工况.选取其中485组作为训练集,50组为测试集,50组为验证集;工况参数组合作为模型输入数据,维度为39;模态系数作为输出数据,维度为1.
3.1 模型类型
采用多种不同类型的机器学习方法对模型进行了训练拟合,并横向对比了不同模型的回归拟合性能.数据集以交叉验证的形式划分为5个不相交集,对每个不相交集的预测准确精度进行评估,能够有效利用有限的数据集,同时可以防止训练数据的过拟合.各模型的超参数调整优化方法均采用贝叶斯优化(Bayesian optimization)[22].为提升模型性能以及消除模型对输入数据任意尺度的依赖,通过标准化将数据转换为平均值为0、标准差为1的数据集,提高模型适应性.
3.1.1 支持向量机模型
支持向量机(support vector machine, SVM)模型在非线性问题和高维度模态识别问题的解决方面具有特定优势,利用支持向量机模型适合解决小样本的回归分析问题.SVM模型优化的超参数包括控制模型对大残差值敏感程度的框约束,控制模型预测规模的核尺度,调整模型预测误差宽容度的Epsilon系数以及决定训练前数据非线性变换形式的核函数.
经训练后使模型性能最优的各个超参数的取值如下:核尺度取值为 1;核函数选取线性核函数;框约束取值为20.653 3;Epsilon取值为19.340 4.
3.1.2 高斯过程回归模型
高斯过程回归(gaussian process regression, GPR)模型在处理回归问题时只需少量数据样本即可获得理想的模型效果[23].GPR模型优化的超参数包括指定了模型先验均值函数形式的基函数,确定响应相关性的核函数,指定初始观察噪音标准差的Sigma,控制模型预测规模的核尺度.
经训练后使模型性能最优的各个超参数的取值如下:基函数设置为常量,核函数选择Isotropic Matern 5/2,核尺度取值为5.980 5,Sigma取值为1 643.406 3.
3.1.3 树集成模型
树集成模型(ensembles of trees, ET)是通过加权组合多个回归树而构成的回归预测模型,多个回归树的组合可以提高回归预测性能[24].ET模型优化的超参数包括指定用于计算每个叶节点响应最小训练样本数的最小叶片大小,调整模型拟合准确性和拟合成本的学习器数量,指定迭代次数的学习率.
经训练后使模型性能最优的各个超参数的取值如下:集成方法设置为袋集成,最小叶大小为 7,学习器数量为 201.
3.1.4 神经网络模型
神经网络模型(neural network, NN)灵活的层次结构通常能够以较高的精度进行预测,网络完全连接层的大小和数量越多,模型越灵活[25].NN模型优化的超参数包括全连接层数、激活函数、正则化强度和全连接层大小.
经训练后使模型性能最优的各个超参数的取值如下:激活函数设置为Tanh,正则化强度(Lambda)取值为6.930 1,第1层大小为29.
3.2 模型性能评估
引入如下2个参数进一步评估模型的准确性和拟合能力.
模型预测的准确性采用均方根误差RMSE进行评估,定义为
(16)
式中,Yo表示观测数值点原始值;Yp表示观测数值点预测值.
均方根误差即预测误差的标准偏差,用于最小化预测误差,量化了2个数据集(训练集和测试集)中的变化量.使用均方根误差作为模型的主要评价指标,其对预测数据的极大误差以及极小误差特别敏感,能够很好地反映预测的准确性.
模型的拟合能力使用决定系数R2进行评估,定义为
(17)
式中,Ymean表示观测数值点的平均值.
决定系数R2表示线性回归模型中由自变量解释的响应变量的变化比例.R2越接近1,线性回归模型解释的变异越大,则拟合回归的效果越好.
各模型均方根误差及决定系数如表5所示.各模型训练后的均方根误差均在同一量级,数值大小差距不明显,其中支持向量机模型和高斯过程回归模型的均方根误差相对较小;对比决定系数参数大小,其中支持向量机模型的决定系数相比其余模型更加接近数值1,即拟合回归的效果更好.因此,综合考虑模型预测准确性和模型泛化拟合能力,最终选取SVM模型作为模态系数的拟合模型.

表5 不同机器学习模型性能参数
4 模型预测结果分析
锅炉速度场快速预测模型运行流程如下:将未知工况参数输入模态系数拟合模型,得到工况参数相对应的模态系数值组合,将模态系数值组合与模态进行组合重构计算获得相应工况参数下的锅炉速度场预测结果.
针对不同负荷值下的工况使用预测模型对锅炉速度场进行了预测计算.图5、图6和图7分别给出了目标锅炉在330、264、198 MW负荷的工况参数下锅炉的A层一次风区域、BC层二次风区域以及SOFA3层燃尽风区域通过CFD数值模拟计算得出的速度场云图和通过本文所建立模型预测计算得出的速度场云图.数值模拟速度场计算结果与模型预测速度场计算结果之间的速度大小的吻合程度通过等高线图表征,其中等高线图的高度代表该处网格的数值模拟结果数值与模型预测结果数值的相对误差.
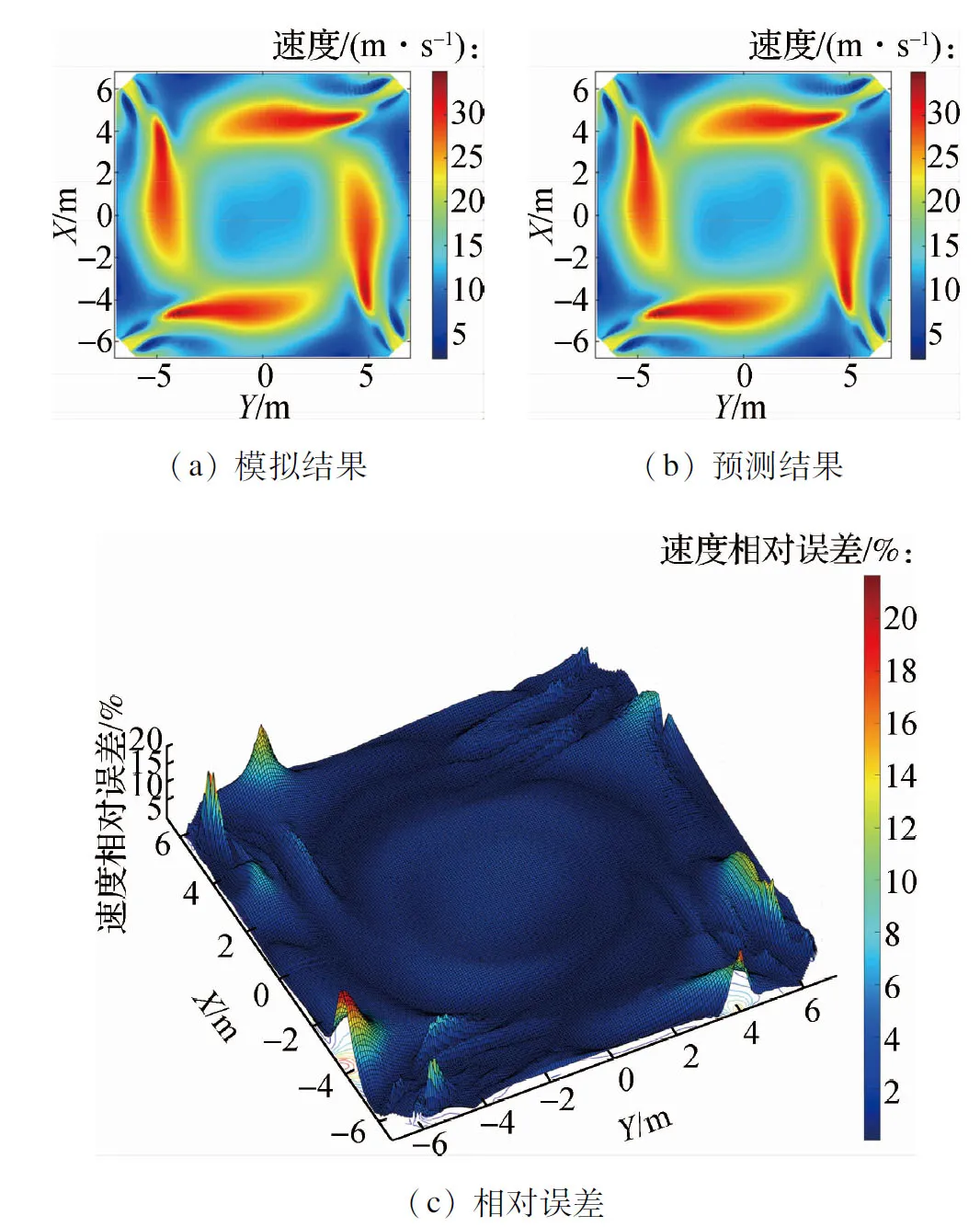
图5 330 MW工况下A层一次风区域速度场预测结果与模拟结果对比
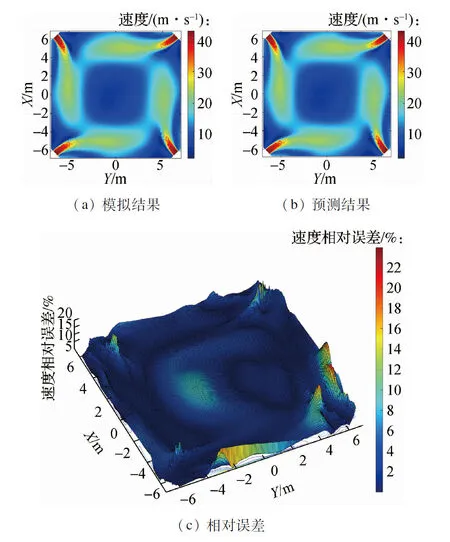
图6 264 MW工况下BC层二次风区域速度场预测结果与模拟结果对比
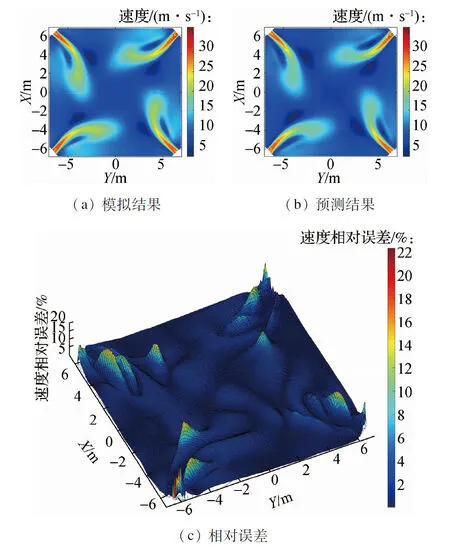
图7 198 MW工况下SOFA3层燃尽风区域速度场预测结果与模拟结果对比
如图5、图6和图7所示,模型在不同负荷工况下的速度场计算结果与数值模拟得出的速度场计算结果基本一致.由速度大小相对误差等高线图可以看出,速度的预测结果数值与模拟结果数值的相对误差整体较小.对所有网格点的预测值与模拟值速度相对误差大小进行统计,计算得出平均相对误差为1.80%,其中相对误差大于10%的网格数量所占总网格数量比例为1.18%,说明速度场的预测结果与模拟结果的数值总体差异较小.
其中,速度预测差值相对较大的区域集中分布在位于锅炉燃烧器四角的燃烧器喷口处的少数网格点,差值最大处的相对误差保持在24%以下,对应速度的绝对误差保持在2 m/s以下.由于喷口周围区域流速相对较大,速度分布可能出现不连续,流场特征信息被含能量较小的模态所表征,从而导致上述燃烧器喷口处速度预测差值相对较大的现象.综上,本文所建立的预测重构模型可以有效地对锅炉速度场的分布信息进行较为准确的预测.
通过均方根误差来计算本文所建立模型的预测速度场与CFD数值模拟速度场的偏差,进一步评估预测重构模型结果的有效性和精确性.
取33 MW为间隔,对165~330 MW下等间隔6种不同负荷下相同网格处的模型预测速度与CFD数值模拟速度的均方根误差RMSE进行了计算,结果如表6所示.

表6 不同工况预测速度均方根误差 m/s
各不同工况参数下预测重构模型的均方根误差均在0.35 m/s以下,满足所需精度要求,证明本文所建立预测重构模型具有较高准确性,能够实现锅炉速度场的高质量高精度预测.
本文计算所采用工作站的CPU型号为Intel(R) Core(TM) i7-10700K,频率为3.80 GHz,内存为32 460 MB,GPU型号为NVIDIA Quadro RTX 4000.通过CFD数值模拟获取锅炉速度场平均计算耗时为169 141.2 s(约2 819 min);而通过预测重构模型获取锅炉速度场平均耗时180.7 s(约3 min),是CFD数值模拟计算耗时的1/936,显著减少了计算时间.相对于CFD数值模拟,本文所建立预测重构模型在便捷性与计算效率上具有较为明显的优势.
5 结论
1) 本文所建立的POD重构模型能够总体把握锅炉速度场的主要特征,可以通过少量的模态重构流场信息,模态累积能量达到流场系统总能量的90%以上即可满足精度要求.
2) 预测模型可以在未预计算的未知工况参数条件下可靠地预测锅炉速度场,预测结果的平均相对误差为1.80%,均方误差小于0.35 m/s.
3) 模型通用性强,计算时间成本低,模型平均耗时(约3 min)是CFD模拟计算平均耗时(约2 819 min)的1/936,使锅炉速度场的近实时获取成为可能,对锅炉运行优化调控具有指导意义,有较高的工程实际应用价值.

