车路协同环境下考虑坡度与前车信息的跟驰模型

陈 龙 刘孟协 蔡英凤 刘擎超 孙晓强

(江苏大学汽车工程研究院， 镇江 212013)

车路协同系统(CVIS)的逐渐成熟，为提高道路交通安全水平和运行效率提供了有力支撑.车路协同系统通过车车通讯/车路通讯获取周围车辆信息和道路信息，全方位实施车车/车路间的动态实时信息交换，为开展车辆主动安全控制[1]和道路协同管理提供了信息基础[2].车路协同交通环境下车辆的跟驰特性发生明显变化[3-5].为研究复杂交通环境下的车辆跟驰行为，改进跟驰模型具有重要意义.

车路协同环境下，车与车、车与路之间的实时信息交互推动了跟驰模型的快速发展[6-10].道路作为车辆运动的载体，其坡度对交通流的影响尤为明显.Li等[11]对最优速度模型进行了扩展，研究了单车道公路坡度对交通流的影响.Komada等[12]通过分析重力对上坡和下坡公路交通流的影响，研究了有坡度高速公路上交通拥堵的发生机理.Zhu等[13]为研究不同坡度道路上交通流的稳定性和密度波，建立了一种考虑坡度的跟驰模型.然而，这些模型均没有考虑相对速度的影响.在实际道路交通环境中，如果前车速度更快，即使车头间距小于安全距离，车辆也不会刹车.为克服上述不足， Zhou等[14]提出了一种考虑相对速度的坡道跟驰模型，研究了坡度和速度差系数对交通流稳定性的影响，数值结果表明引入相对速度可以抑制交通拥堵.Wang等[15]提出了一种流体动力学跟驰模型，该模型考虑了坡度道路上的交通流中断概率，结果表明交通中断概率和坡度会影响系统稳定区域.Jiao等[16]为探讨倾斜道路对交通流的影响，提出了一种考虑电子节气门和驾驶员特性的坡道跟驰模型.上述研究均表明，道路坡度对交通流具有显著影响，但对于多车间的相互作用尚未深入考虑.

对于交通流中多车间的相互作用，也有部分研究涉及[17-18].为探索多前车的速度变化趋势对交通流的影响，Guo等[19]提出了考虑多前车速度波动的跟驰模型.秦严严等[20]通过引入多前车电子节气门角度反馈，构建了智能网联车辆跟驰模型.仿真结果表明，考虑前车数量越多，多前车反馈权重系数越大，模型的稳定性越好.纪艺等[21]提出了一种基于多前车最优速度与紧邻加速度的智能网联车辆跟驰模型，该模型在合理加速度敏感系数和前车数的约束下，速度和车头距波动幅度相对较小，且能较好地吸收交通扰动和增强车队的行驶稳定性.Peng等[22]考虑了驾驶员视野中多前车和后车的动态行驶信息，对全速差模型(FVDM)[23]进行了改进，结果表明，改进后的模型与实际交通数据更吻合.Li等[24]建立了综合考虑多前车平均速度和电子节气门角度的跟驰模型，该模型考虑的车辆信息更多，车流的稳定性更好.

尽管现有研究在单独考虑道路坡度和多前车信息方面已有涉及，但既没有综合考虑道路坡度和前车信息的协同影响，也没有从定量的角度分析前车信息对跟驰车辆的作用，难以适应更为复杂的车路协同交通环境.因此，为揭示车路协同交通环境中各交通要素间的耦合机理与复杂运行规律，提高交通流的稳定性，本文在FVDM的基础上，考虑道路坡度和前车信息，建立车辆跟驰模型，并研究坡度和前车权重系数对交通流的协同影响机制.

1 车路协同下车辆跟驰特性

1.1 车路协同交通环境

车路协同系统作为当今智能交通领域的前沿技术之一，利用最新的无线网络通讯前端技术，将人-车-路3个要素紧密结合，形成有序、整体的闭合交通系统.车路协同系统最主要的2个子系统是路侧单元(RSU)和车载单元(OBU)，RSU和OBU以无线通信方式来实现车辆与车辆、车辆与路侧以及路侧与路侧之间的信息传输和共享[25].

在多渠道的动态交通信息融合作用下，车路协同环境使信息获取与交互手段、内容和范围发生了重大变化.传通交通环境与车路协同交通环境差别主要体现在信息获取、处理和驾驶员/车辆反馈等方面，具体差异如表1所示.

表1 传统交通环境与车路协同交通环境的差异

1.2 车辆跟驰特性

与传统交通环境不同，车路协同交通环境下车辆跟驰特性发生变化[26-27].车辆在跟驰行驶时处于非自由运行状态，车队具有如下3个特性：

1) 制约性.车路协同交通环境中车辆仍受车速和间距的制约，但车间安全距离减小，最大行驶速度增大，车辆间的制约性减弱.

2) 延迟性.车路协同交通环境下，由于车载系统的动态感知取代了传统交通环境中驾驶员自身的感知与判断，总反应时间呈减小的趋势.

3) 传递性.车路协同交通环境下，车车/车路之间通过无线通讯进行交互传递.虽然存在一定的系统延迟和通信延迟，但相较于传统的交通环境，其延迟可忽略不计，故传递的范围和速度大幅提高.

这表明，车路协同交通环境下各种动态交通信息能够明显提高驾驶员对外界环境的感知和对车辆行驶状态的决策能力，使得车辆的跟驰行为也与传统交通环境下有所不同.因此，单一考虑车辆因素或道路因素，已无法正确刻画车路协同环境下的车辆跟驰行为.

2 模型建立

2.1 坡道车辆动力学分析

为分析车辆在坡道上的跟驰行为特性，根据牛顿第二定律可知，车辆在坡道上(上坡为例)的动力学方程可表示为

ma=F-μmgcosθ-mgsinθ

(1)

式中，a为车辆的加速度，m/s2；F为车辆驱动力，N；θ为道路坡度角；g为重力加速度，m/s2；m为车辆质量，kg；μ为道路摩擦系数.

由式(1)可知，车辆所受到的重力分力随着道路坡度的变化而变化，上坡时坡度对车辆运动产生抑制作用，下坡时坡度对车辆运动产生积极作用.安全车头间距是车辆紧急制动时不与前车发生碰撞所需的制动距离.由于上坡时，坡度对车辆运动产生阻碍作用，这使得车辆在制动过程中所需的制动距离较小；而下坡时，坡度对车辆运动产生积极作用，使得车辆在制动过程中所需的制动距离较大.因此，车辆在坡道跟驰行驶中与前车保持的安全车头间距hc,θ可表示为[13]

(2)

式中，hc为无坡道路上的安全车头间距，m；η和ξ为相关系数，为简单起见，取η=ξ=1.

除安全车头间距的差异，车辆在不同坡度道路行驶时所表现出来的最大行车速度也不同.据文献[13]对车辆在坡道行驶的最大速度的研究，发现下坡时，坡度通过重力分力对车辆行驶速度产生强化作用；而上坡时坡度对车辆的速度产生弱化作用，并且这种强化或弱化作用会随着道路坡度的增加而增加，因此车辆在坡道上行驶的最大速度vg,max可表示为关于坡度的函数，即

vg,max=vmax(1∓βsinθ)

(3)

式中，vmax为车辆在无坡道路上行驶的最大车速，m/s；β为常数，取值为1，取“-”表示上坡，取 “+”表示下坡.在足够大的车头间距范围内，上坡时车辆以最大速度vmax-sinθ向前行驶，下坡时车辆以最大速度vmax+sinθ向前行驶.

2.2 灰色关联分析

基于V2V(vehicle-to-vehicle)通讯技术，车路协同环境中的车辆在运动过程中可以获取前方多车辆的动态行驶信息，将车辆信息考虑到跟驰模型中，发现考虑的车辆数量越多，交通流的稳定性越好[19-24].但是，当考虑的前车数量过多，对RSU和OBU的性能要求越高，增加了设备成本.实际上，随着前方车辆与目标车辆之间的距离增加，前方第3辆车或更前方车辆对跟驰行为的影响降低[20].因此，本文只考虑前2辆车对目标车辆的影响.

然而，以往诸多研究对于车辆信息的考虑大多依靠经验，具有主观性.为此，本文利用真实的NGSIM项目数据集，提取了连续跟驰的3辆车(目标车n、前导车n+1、前导车n+2)的20组车辆跟驰数据，如表2所示.其中an(t)、vn(t)为目标车n在t时刻的加速度和速度，Δxn(t)、Δvn(t)分别为t时刻前导车n+1与跟随车n之间的相对位置和速度差，Δxn+1(t)、Δvn+1(t)分别为t时刻前导车n+2与前导车n+1之间的相对位置和速度差.

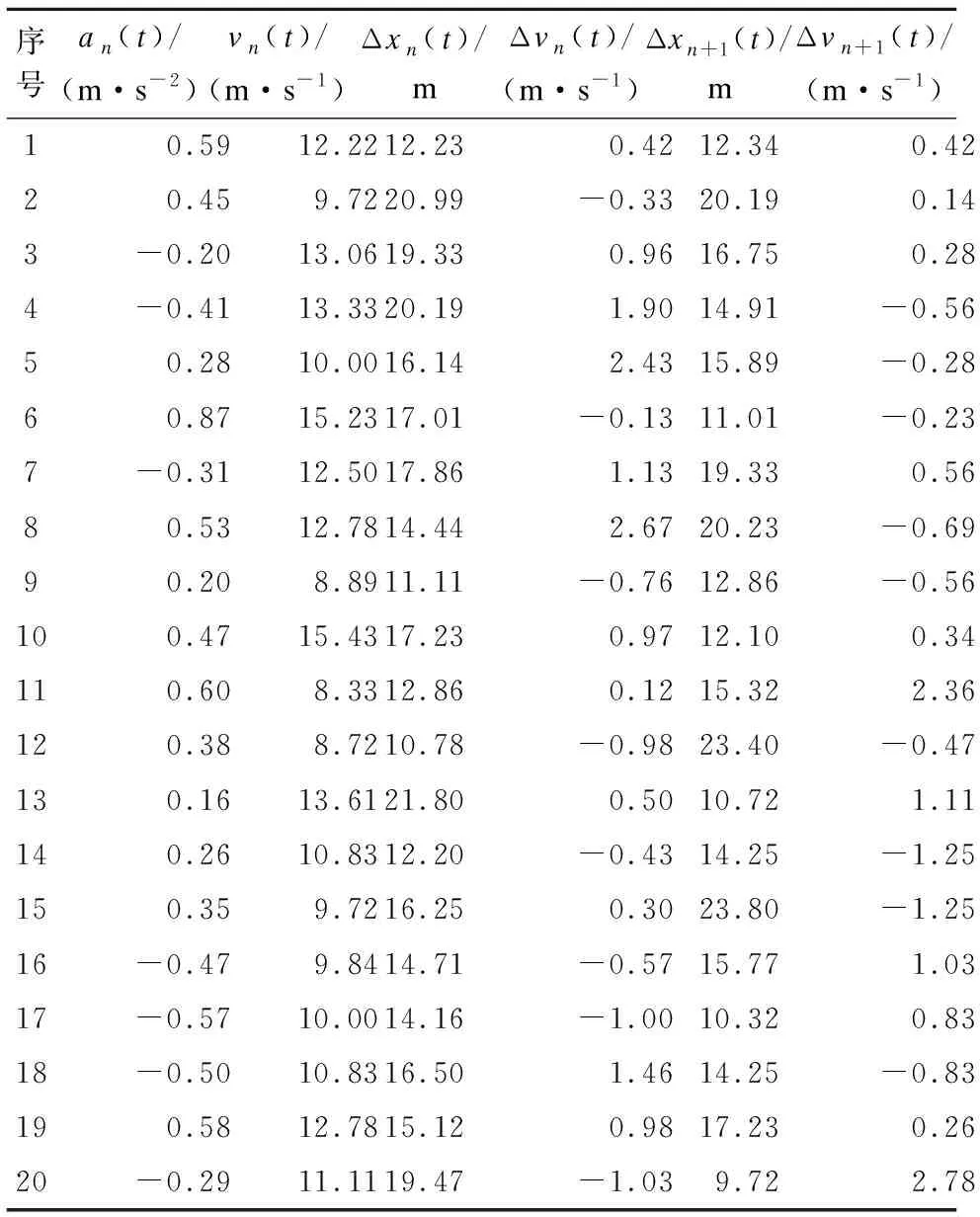
表2 车辆跟驰数据

为确定前2辆车的不同类型信息对目标车辆跟驰行为的影响程度，基于表2中的车辆跟驰数据，通过灰色关联法来探寻vn(t)、Δxn(t)、Δvn(t)、Δxn+1(t)、Δvn+1(t)这5种车辆信息与目标车辆n加速度an(t)的关系.表3给出了这5种车辆信息与目标车辆加速度的关联度值.

表3 车辆信息与目标车辆加速度的关联度

根据灰色关联理论，关联度越大，说明该信息对目标车辆加速度的影响程度越大.由表3可知，vn(t)、Δxn(t)、Δvn(t)、Δxn+1(t)、Δvn+1(t)与目标车辆加速度之间的关联度均大于0.5，说明这5种车辆信息对目标车辆加速度都有显著影响，特别是vn(t)、Δxn(t)和Δvn(t)对目标车辆的加速度影响更大.这也证实了距离目标车辆越远，影响程度越小.

2.3 改进模型

Jiang等[23]提出的FVDM是经典跟驰模型之一，其考虑了全速差项的影响，能够比较全面地描述传统交通环境下车辆的跟驰行为.模型如下：

(4)

式中，xn(t)为车辆n在t时刻的位置，m；α为敏感系数，即车辆各系统反应时间与驾驶员反应时间总和的倒数，s-1；λ为对速度差Δvn(t)的响应系数；V(·)为优化速度函数，其表达式为

(5)

基于车路协同环境下坡道跟驰特性和前车信息对车辆跟驰行为的影响分析，本文在FVDM的基础上，提出了车路协同环境下考虑道路坡度和前车信息的智能网联车辆跟驰模型，图1为车路协同环境下考虑坡度与双前车信息的跟驰场景.

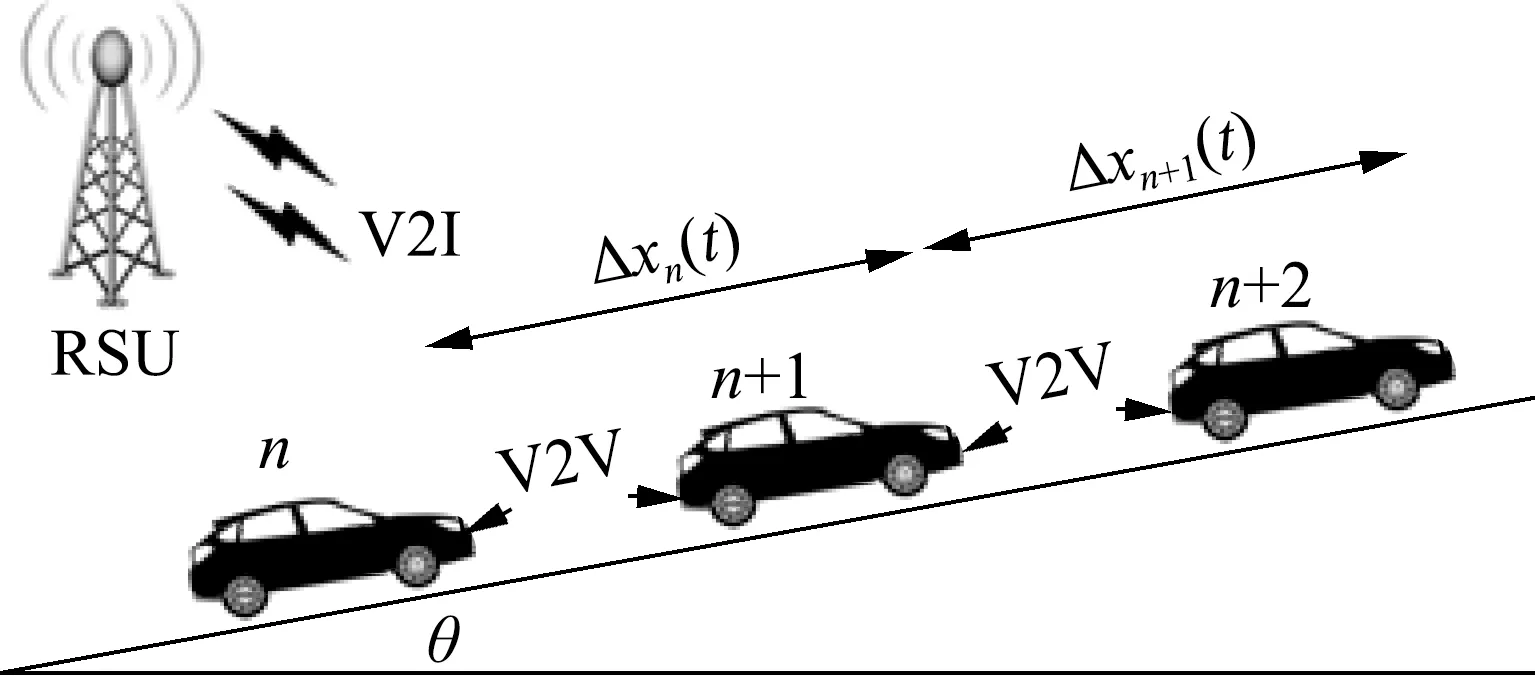
图1 车路协同环境下考虑坡度与双前车信息的跟驰

场景

本文改进模型如下：

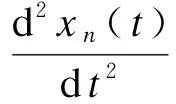
λG(Δvn(t),Δvn+1(t))

(6)

式中，Vp,θ(·)为同时考虑道路坡度和前车信息时的优化速度函数；G(·)为加权速度差函数.函数Vp,θ(Δxn(t),Δxn+1(t))和G(Δvn(t),Δvn+1(t)) 的表达式如下：

(7)

Δx=(1-p)Δxn(t)+pΔxn+1(t)

(8)

G(Δvn(t),Δvn+1(t))=(1-p)Δvn(t)+pΔvn+1(t)

(9)

式中，p为前导车n+2的权重系数，则1-p为前导车n+1的权重系数，0≤p<0.5.

通过建立考虑坡度和前车信息的跟驰模型，来描述车路协同环境下智能网联车辆的跟驰行为，不仅可以研究坡度对跟驰行为的影响，还能剖析多车间的相互作用.由式(6)、(7)可知，当p=0、θ=0时，本文改进模型退化为FVDM，因此本文模型更具有一般性.

3 线性稳定性分析

利用微扰动法分析本文改进模型的稳定性，研究交通流在坡道上的演变规律.假设交通流在初始时刻为稳定状态，即前后车辆间保持一致的车头间距b与最优速度Vp,θ(b).因此，针对稳定行驶的交通流，第n辆车的实时位置可表示为

(10)

(11)

将式(11)代入式(6)中，可得

y″n(t)=α{Vp,θ((1-p)(b+Δyn(t)+
p(b+Δyn+1(t)))-y′n(t)-Vp,θ(b)}+
λ(1-p)Δy′n(t)+λpΔy′n+1(t)

(12)

进而将式(12)通过泰勒公式展开并忽略高阶项，可得如下线性化方程：

y″n(t)=α(1-p)[V′p,θ(b)Δyn(t)-y′n(t)]+
αp[V′p,θ(b)Δyn+1(t)-y′n(t)]+
λ(1-p)Δy′n(t)+λpΔy′n+1(t)

(13)

其中，

(14)

Δyn(t)=yn+1(t)-yn(t)

(15)

Δyn+1(t)=yn+2(t)-yn+1(t)

(16)

将式(13)中的yn(t)按傅里叶级数展开，令yn(t)= exp(ikn+zt)，可得

z2+{α-λ[(1-p)(eik-1)+p(e2ik-eik)]}z-
αV′p,θ(b)[(1-p)(eik-1)+p(e2ik-eik)]=0

(17)

将z按z=z1(ik)+z2(ik)2+…展开，并将其代入式(17)，得到z表达式中一阶项(ik)和二阶项(ik)2的系数，如下所示：

(18)

如果z2为负，则初始均匀的稳定流将会变得不稳定，反之将保持原有的稳定流状态不变.因此，可得到如下稳定性临界条件：

(19)

对于具有长波长的小干扰，均匀交通流在以下条件下是稳定的：

(20)

根据稳定性临界条件可知，当p=0、θ=0时，得到与经典的FVDM一致的稳定性条件：

α>2V′(b)-2λ

(21)

当稳定性条件式(20)得到满足时，施加小干扰的交通流是稳定的，反之则交通流会演变成走走停停的交通拥堵状态.与FVDM的稳定条件式(21)相比，改进的模型通过引入前导车n+2对跟驰车的影响，使稳定性临界点下移，本文改进模型的稳定性提高.

为直观描述稳定性的变化趋势，根据式(19)，得到了λ=0.2时，p和θ取不同值情况下的模型稳定性临界曲线，如图2和图3所示.图中临界曲线的上部分表示交通流稳定区域，下部分表示非稳定区域.

由图2可知，交通流在上坡阶段，稳定性临界曲线随着θ的增加而逐渐左移.当θ=0°时，车流的安全车头间距为4.00 m；当θ=3°时，安全车头间距为3.80 m；当θ=6°时，安全车头间距为3.58 m.由图3可知，交通流在下坡阶段，稳定性临界曲线随着坡度θ的增加而逐渐右移.当θ=0°时，车流的安全车头间距为4.00 m；当θ=3°时，安全车头间距为4.20 m；当θ=6°时，安全车头间距为4.42 m.这表明：上坡过程中交通流的平均车头间距随着坡度角的增加而减小，车辆分布比较密集；下坡过程中交通流的平均车头间距随着坡度角的增加而增加，车辆分布较为稀疏.该结论与实际坡道道路上的交通流车头间距分布情况一致.

对比图2和图3中不同θ时的临界曲线可以发现：对于上坡情况，每条曲线的顶点随着θ值的增加而下降，这表明稳定性区域随着θ值的增加而扩大；对于下坡情况，稳定区域随着θ的增加而缩小.具体而言，交通流的稳定性随着不同情况(上坡或下坡)下的坡度变化而变化.其原因是，当在上坡道路上运行时，车辆行驶相对缓慢，而当在下坡道路上运行时，车辆以更高的速度移动，车辆的堵塞变得比上坡情况更多.

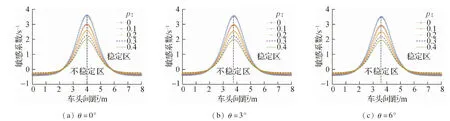
图2 上坡阶段模型稳定性临界曲线

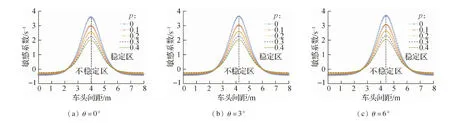
图3 下坡阶段模型稳定性临界曲线

综合分析图2和图3可知，交通流无论在上坡还是在下坡，当道路坡度一定，稳定性临界曲线随着p的增加而逐渐下移，反映出模型的稳定性随着p的增加而提高.这说明同时兼顾前方2辆车的车头间距和速度信息可以提高模型的稳定性.

4 数值仿真与分析

为验证理论分析的正确性，研究道路坡度和前车权重系数对交通流的影响，不考虑智能网联车辆的结构和性能差异性，并且忽略车与车、车与路之间的通讯干扰影响，对本文改进模型在加速启动和微扰动场景下进行仿真，探寻交通流的实际演化行为.模型仿真参数设置为[14]：α=2.5 s-1，λ=0.2，vmax=4 m/s，hc=4 m.

4.1 车辆启动仿真

本节对车辆启动的情况进行仿真.车辆启动过程中模拟场景如下：当t<0 时，交通信号灯为红灯，车队由8辆车组成，每辆车的位置为xn=(n-1)Δxn，其中n=1,2,…,8，车头间距Δxn=4 m，车辆均处于静止状态，即vn(0)=0.在t=0时刻，交通信号灯由红色转为绿色，头车以加速度a=2.15e-0.5t开始启动，随后各辆车依次开始启动.

图4和图5分别为θ和p取不同值时车队启动过程中每辆车的速度和加速度的变化情况，图中每条曲线代表一辆车.以第7辆车为例，车队启动时其速度波动次数及加速度波动幅度情况如表4所示.

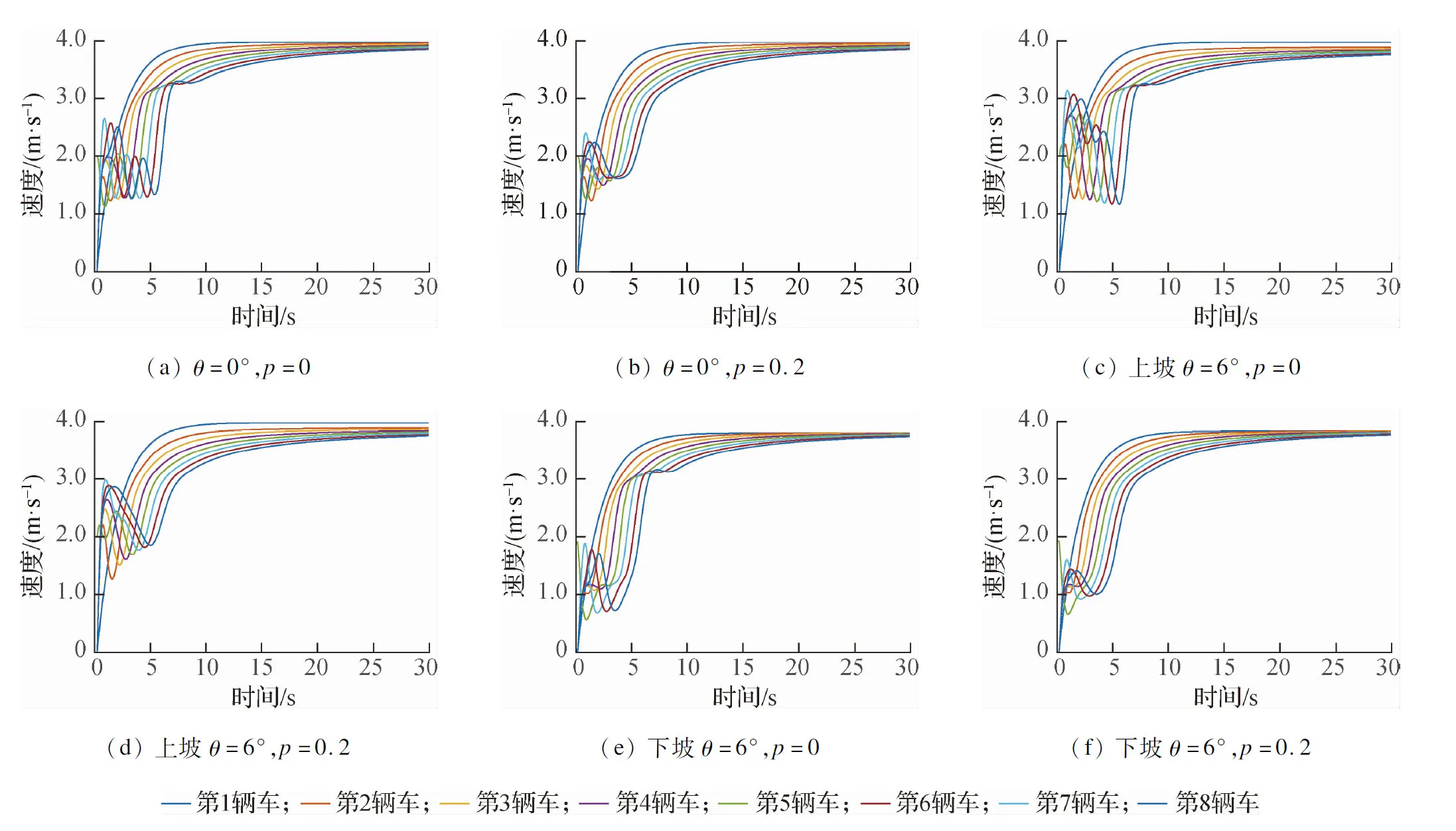
图4 车辆启动过程的速度变化

由图4(a)、(c)和(e)和图5(a)、(c)和(e)可知，车辆在启动阶段时速度和加速度的波动情况随着道路坡度的不同有明显差异.以第7辆车为例，当θ=0°、p=0时，车辆的最大加速度为4.997 m/s2；当上坡θ=6°、p=0时，最大加速度为6.787 m/s2；当下坡θ=6°、p=0时，其最大加速度为3.094 m/s2.这是因为上坡时，车辆的重力分力对车辆的启动加速具有抑制作用，为克服这种抑制作用，保证车辆顺利跟随启动，车辆所产生的加速度较大；而在下坡时，重力分力对车辆启动产生积极作用，为保证与前车的安全车距，车辆的加速度略小.这说明本文改进模型能够很好地描述在具有坡度道路上车辆的启动特性.

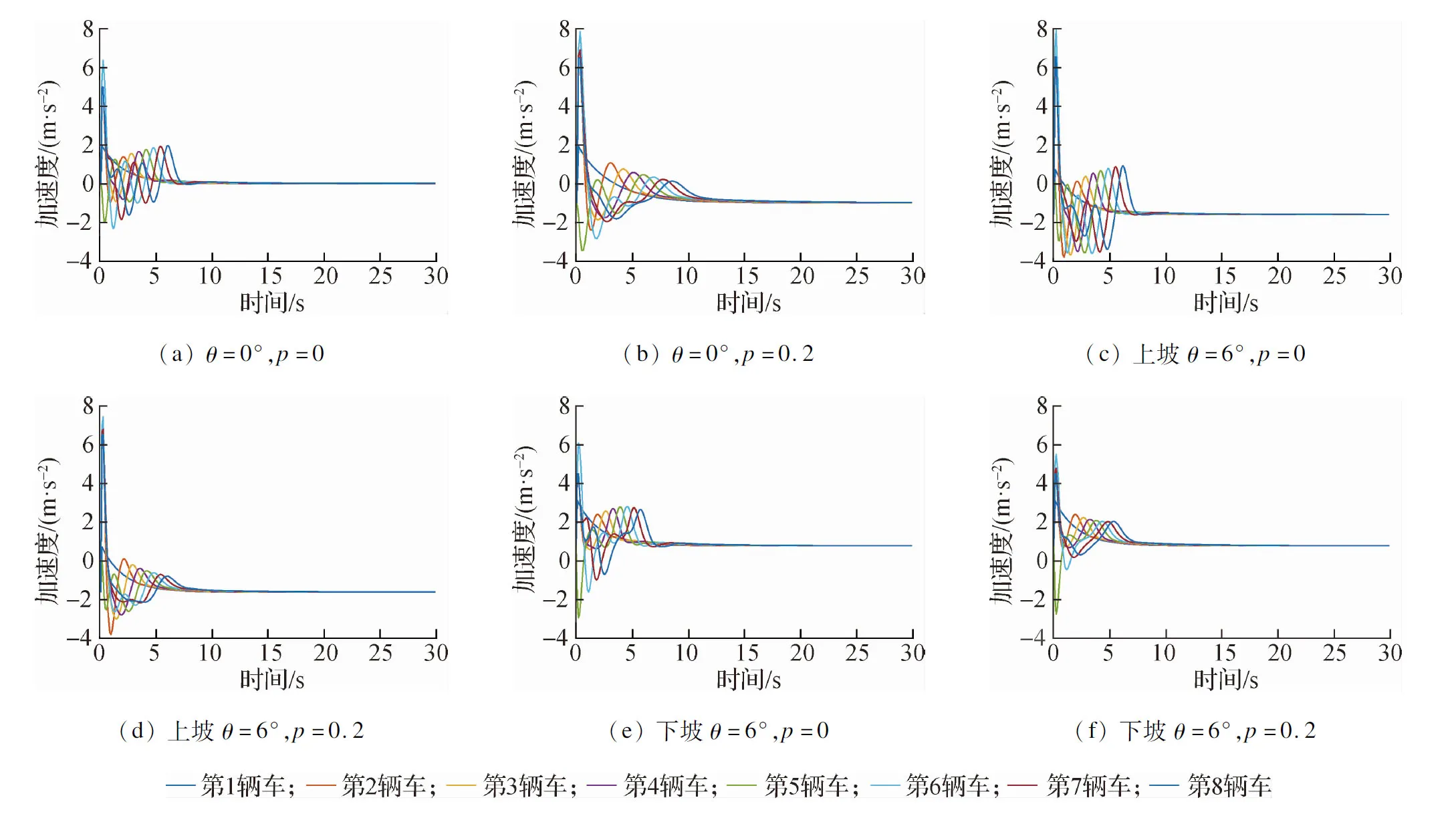
图5 车辆启动过程的加速度变化

由表4可知：与p=0相比，当p=0.2时，车辆启动时的速度波动次数和加速度波动幅度均有明显减小.当θ=0°时，加速度波动幅度减小22.1%；当上坡θ=6°时，加速度波动幅度减小11.0%；当下坡θ=6°时，加速度波动幅度减小15.8%.因此，考虑双前车的速度和车头间距信息能减小速度波动次数和加速度波动幅度，提高车队启动时的稳定性.

表4 第7辆车的速度波动次数及加速度波动幅度

4.2 微扰动仿真

为进一步验证前车权重系数p对坡道上交通流稳定性的影响，本节将对由100辆车组成的车流进行微扰动仿真.通过对稳定车流的头车施加小干扰，分析车头间距的波动情况，从而验证p对交通流的影响.记第1采集时刻为初始状态，车辆初始状态设置如下：

vn(1)=Vp,θ(hc,θ)

(22)

xn(1)=(n-1)hc,θ

(23)

式中，n=1,2,…,100.

图6给出了交通流在3种坡度道路上的车头间距演变情况.由图可知：当p=0时，3种坡度下交通流的车头间距均未收敛至安全车头间距，车流未恢复至稳定状态；随着p的增大，车头间距波动明显减小；当p=0.4时，车头间距波动基本消除，交通流重新达到稳定状态.这说明车路协同环境下考虑双前车信息能够很好地吸收车头间距波动，使交通流加快恢复稳定状态，增强交通流的稳定性.

图6 车头间距演变情况

5 结论

1) 现有跟驰模型未能兼顾道路条件和多车辆信息的影响，导致无法准确描述车路协同环境下车辆的跟驰行为，因此在FVDM的基础上，建立了车路协同环境下考虑道路坡度和双前车信息的智能网联车辆跟驰模型.

2) 本文模型充分考虑了车辆在坡道行驶时的特性，能够很好地描述坡道上车辆的跟驰行为.同时，通过引入双前车的车头间距和速度差信息，能够很好地吸收交通流的速度和车头间距波动，增强交通流的稳定性.

3) 本文模型仅考虑了道路条件中坡度这一因素，未来尚需更加全面地考虑道路曲率、附着系数和超高等因素对跟驰行为的影响，构建更加符合车路协同交通环境下的跟驰模型，从而提高交通系统演化规律的分析准确性.