基于粒子群算法的智能换相策略

余振洲，许志红

(福州大学电气工程与自动化学院，福建省新能源发电与电能变换重点实验室, 福建 福州 350108)

0 引言

随着电气化水平提高，城市或农村的用电量随之增大，配电台区用户端的负荷大多为单相，且在三相上分布不均匀，使用时间段也具有不确定性，因此产生三相负荷不平衡现象[1].我国供配电方式多为三相四线制，这种状态的长期存在，使线路损耗增大.三相线路出现重载或轻载等情况的出现，不利于用电设备长期运行，对供电质量影响较大.因此，需使用可靠的方法来解决不平衡问题.

目前，针对此问题我国常用的方法为人工换相和使用智能换相装置[2].人工换相不仅费时费力，而且还会存在换相停电问题，在当前智能化电气环境下，并不是一个理想的解决方案.智能换相装置由两部分组成，其中主控装置收集三相电压、电流信息，制定换相策略，换相开关作为执行机构，调整负荷相别使负荷在三相上的分布尽可能达到平衡.在主控装置中，通过智能算法根据当前的电量信息，优化出满足要求的换相方案，是智能换相开关的关键技术.本文针对智能换相策略要求，基于粒子群算法建立最佳换相策略数学模型，优化换相结果以指导负荷调整相别.并对粒子群算法本身的缺陷进行迭代改进，使优化结果更佳、迭代速度更快.经仿真和试验验证表明，改进后的粒子群算法所建立的智能换相策略，能够有效解决三相负荷不平衡问题.

1 三相不平衡概念及计算

在三相电压、电流的幅值大小、频率相同，且相位相差2π/3的情况下，电力系统运行状态视为理想状态.但在实际应用中，因为各负荷随机分布导致不平衡现象的产生，三相不平衡度超过电网的标准，即视为三相不平衡状态.在这种状态下，中性线产生较大电流，极大地影响了电网的运行.

目前对于不平衡计算的标准较多，国内外对于三相不平衡度的判定主要是通过电流法和电压法两种方法[3]，电流不平衡度计算方法在实际工程中更常被应用且电流信息在计算结果上更能准确表示实际不平衡度大小，因此本文计算不平衡度通过电流来判定，公式表示为：

(1)

式中：σA、σB、σC分别为A、B、C三相的电流不平衡度；IA、IB、IC分别为A、B、C三相的相电流；Iav为电流平均值.

2 三相负荷不平衡仿真分析

低压配网台区中各相负荷不平衡状况的产生主要是因为用电负荷的分布不均匀，进而影响电网的正常运行情况.现使用MATLAB/Simulink软件搭建模型模拟低压配电台区不均匀分布负载情况，从仿真角度研究当负荷在各相的分布处于不平衡状态时，对配电系统所造成的影响，仿真模型如图1.

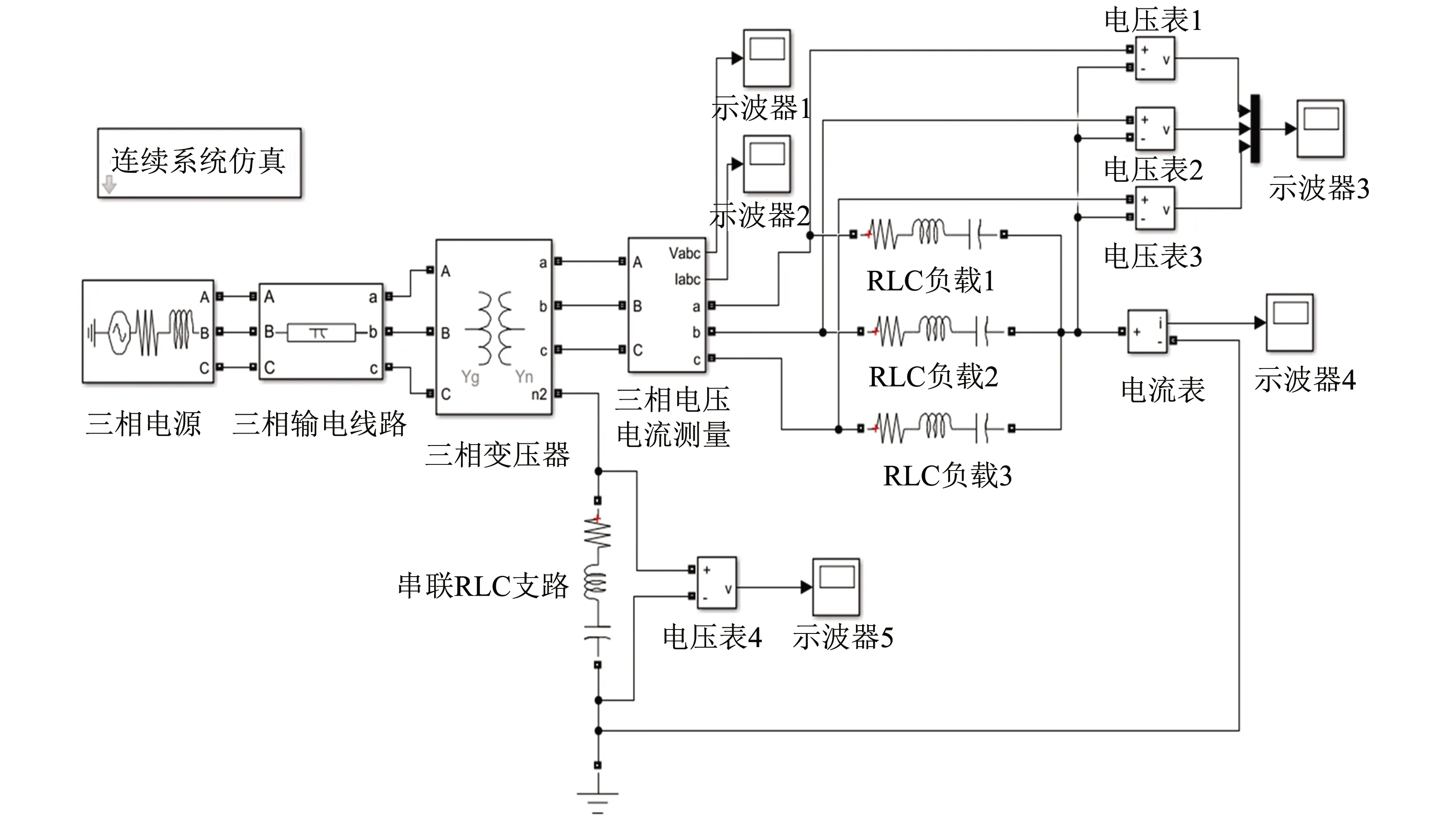
图1 低压配网三相负荷不平衡模型Fig.1 Three-phase load imbalance model for low-voltage distribution network

仿真设置参数为： 电源10 kV, 传输线路10 km，经过10/0.38 kV的变压器传送给三相负载，中性线接地电阻阻值为5 Ω，A、B、C三相负荷分别设置为40、60、80 W，仿真时间0.1 s.此系统为三相负荷不平衡系统，由于负荷不平衡，导致三相负荷上电压波形差异较大，运行时三相负荷上电压波形如图2所示.

由图2可看出，在不平衡的情况下，A、B、C三相负荷上的电压有较大差距，这种状态导致中性线上有电流存在，且中性线上的阻值较大，长期运行会在中性线上产生较多线路损耗，同时不利于设备的长期使用.因此及时并有效地解决负荷不平衡问题在电网运行中尤为重要.与其他国内外解决措施, 如无功补偿、三相相序自动转换器、人工换相相比较，使用智能换相开关是一种快速准确且更为智能化的方法[4-6].

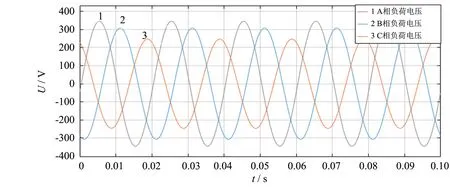
图2 三相负荷电压波形Fig.2 Three-phase load voltage waveform network

3 智能换相策略的建立

智能换相实际上就是将A、B、C三相上的用户侧各用电设备重新分配，使负载在各相上的分配尽可能一致，从而使三相达到负载平衡的状态[7].在换相时，需要考虑以下两点： 1) 由于用户侧负荷随机性较大，在换相执行过程中并不能保证换相后的负荷完全均匀分布在三相，因此应使得换相后的不平衡度尽量处于较低的状态；2) 每一次切换相别指令的执行都伴随着换相装置的动作，由于过多动作会使换相装置使用寿命减少，因此在制定换相策略时，应使换相装置避免频繁动作，从而保障了换相开关能够长期使用，且能够满足整体上的节省开支等实际问题.

3.1 最小的三相不平衡度

假设在配电台区有N个换相执行装置，每个换相开关当前所连接负荷的相别通过二进制编码可以用向量K表示：

(2)

用矩阵KX表示配电台区中各换相装置所接入三相的相别.KX表示为：

KX=[K1,K2,K3, …,KN]

(3)

三相电流设为IA、IB、IC，假设每个用户侧的电流都为I，每相上的电流之和可以用该相上的用户端电流与所接相序的开关状态的乘积表示，则换相前电流可以表示为：

[IAIBIC]T=K×I

(4)

换相后，负载前的换相开关所接的相别变化，矩阵为K′, 各相电流分别为IA、IB、IC，矩阵表示如下：

[IaIbIc]T=K′×I

(5)

已知不平衡度的计算方法，采用式(1)来计算换相前后的不平衡度，换相后的三相不平衡表示如下：

(6)

故以最小不平衡度为寻优目标所建立的寻优函数为：

δ1=min{σ(K)}

(7)

3.2 最少的换相动作

智能换相开关具有一定的机械寿命和电气寿命，且换相过程会带来不可避免的断电时间，在不平衡度达到国家标准的前提下，过程中所动作的开关数量越少越好，以减少对系统的影响[8-9]. 相别转换之前的相别矩阵为K，转换后的相别矩阵为K′，用D表示相别转换的次数，若换相前后开关动作导致所接入的相别发生变化，则D为1，若开关接入的相别状态在换相前后没有发生变化，则D为0. 故开关动作总次数D(K)表示如下：

(8)

则以最少换相动作为寻优目标所建立的数学函数为：

δ2=min{D(K)}

(9)

综合以上两点，本次换相策略所建立的数学函数表示如下：

δ1=min{σ(K)};δ2=min{D(K)}

(10)

式中：δ1为最小不平衡度的寻优函数；δ2为最少的相别转换次数的目标函数；σ(K)为不平衡度；D(K)为换相开关接入相别发生变化的次数.

同时还存在一些约束条件，如： 优化过程中开关状态矩阵只有[1 0 0]T、[0 1 0]T、[0 0 1]T三种，分别表示接入A、B、C三相；优化后的不平衡度要小于国标下的标准, 否则重新进行迭代，且优化后负荷侧各开关接入某相的电流不能过大等，在采用智能算法求解三相不平衡问题的时候都要考虑到.

4 优化算法求解最优换相

多目标函数建立后，寻求一个合适的算法对其进行求解，在国内外众多优化多目标的算法中，一般有粒子群算法、蚁群算法及均值聚类算法等. 在求解智能换相策略中，粒子群算法能够快速收敛，在多个寻优目标方面具有较大优势而且编程复杂度低，本文采用粒子群算法来求解换相最优策略.

4.1 粒子群算法理论

粒子群算法(particle swarm optimization，PSO)是由Eberhart和Kennedy于1995年提出[10-11].粒子在搜索过程中，每个粒子视为一个个体，并且具有速度特征和位置特征，分别表示移动的快慢和方向.在迭代过程粒子的速度和位置会不断更新变化，从而得到全局最优迭代值.V和X的更新计算公式为：

(11)

式中：i为种群的第i个粒子；j为搜索维度；ω为惯性因子，通过调整ω的大小，可以调整粒子在迭代过程寻找最优解的能力；c1和c2为加速常数，常设为c1=c2=2，但不是一定的，一般取值范围在c1=c2∈[0, 4]；random(0, 1)为随机数，区间在[0, 1]上；pbesti为每个粒子寻优的极值；gbest为整体上极值.

4.2 仿真分析

以某低压配电台区15个换相开关所接负荷与相序为仿真数据进行仿真实验，每个负荷的电流与所接入的相别如表1所示.由表1数据，根据式(6)和式(8)分别建立不平衡度最小和换相开关动作次数最少的目标函数，以当前各相电流及相别的状态矩阵为求解变量，以式(10)建立的多目标函数为适应度函数进行优化计算.

表1 某配电台区换相前各相电流及相别

经过计算可得，A、B、C三相的电流分别为129、95、75 A，平均值为99.67 A，通过式(1)可得，此区域的三相不平衡度为29.7%，超出国标中规定的三相不平衡标准.

换相前开关所接负载相别的矩阵为K，表示如下：

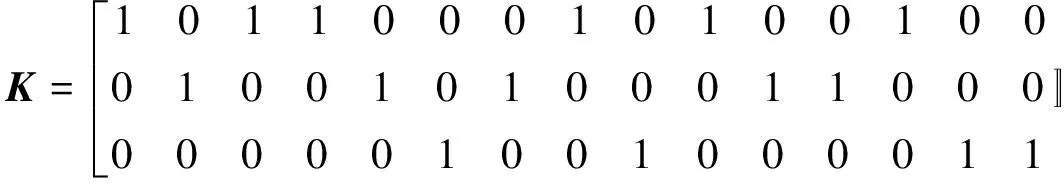
(12)

利用粒子群算法优化此配电台区的三相负荷所接相序的开关状态，通过MATLAB软件计算，其中参数设置c1=c2=2，ωmax=0.9，ωmin=0.7，粒子数设为100.结果如下，各开关换相后的状态矩阵为K′.

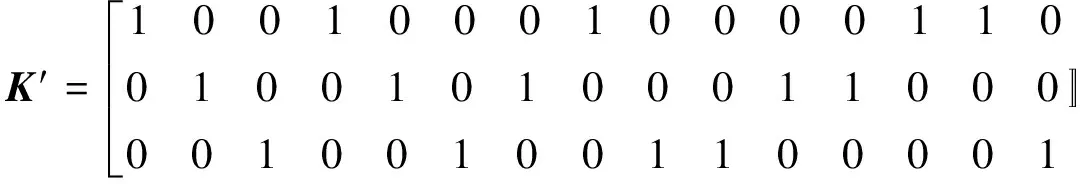
(13)

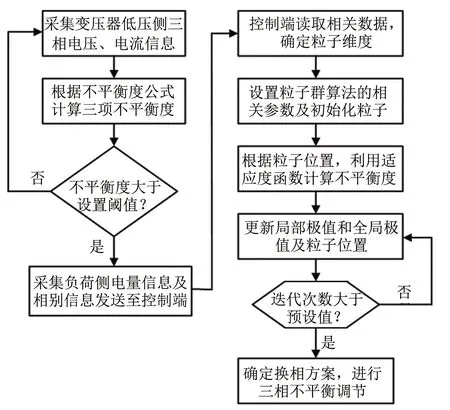
图3 粒子群算法流程图Fig.3 Particle swarm algorithm flow chart

从式(13)可看出，有三个换相装置接入的相别在换相前后状态发生改变，其中3号和10号开关从A相换到了C相，14号开关从C相转到了A相，经过这三组开关所接相序的改变，可以计算得出，换相后IA为103 A，IB为95 A，IC为101 A，三相不平衡度为4.73%，对比换相前的29.7%，不平衡度有了比较明显的降低，算法的优化流程如图3所示.

然而粒子群算法也存在较大的不足，计算时粒子会提前收敛，并不是整体上的最佳计算结果，收敛速度在迭代后期会变慢[12-15]，针对此算法的这个缺点，需要对其寻优过程做出优化.常用的做法是在粒子迭代产生最优解时，只考虑使用位置属性来描述粒子的搜索过程，使粒子在寻找最佳计算结果的过程不会出现提前收敛.改进后粒子群算法的表达公式如下：

x(t+1)=(1-β)x(t)+βρg(t)+αε(t)

(14)

式中：ρg为在当前计算中的全局最佳优化结果；ε为在[0, 1]中的随机向量；α=γt(0<γ<1)；β∈(0.1，0.7).

图4中，曲线1为三相不平衡度优化过程，曲线2为三相不平衡度和开关动作次数的总函数计算过程.使用PSO算法对优化函数进行迭代计算时，当迭代达到63次时，三相不平衡度函数和总适应度函数开始收敛.由图4(b)可得出，改进后粒子群算法的三相不平衡适应度函数在迭代20次左右开始收敛，与改进前算法的计算结果做比较，改进后粒子群算法在计算上能够更快速地到达收敛状态.

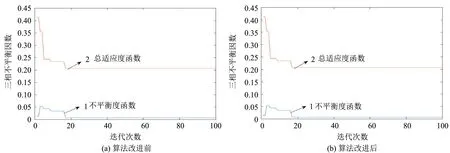
图4 三相不平衡适应度收敛曲线 Fig.4 Convergence curve of three-phase imbalance fitness

经过改进PSO优化的换相装置动作开关矩阵为K3，表达式如下：

(15)

可以看出，本次计算结果中，换相后A、B、C三相电流大小分别为99、100、100 A，电流不平衡度大小为0.68%.与换相前的开关接入相别相比，开关产生了4次换相动作，分布如表2.

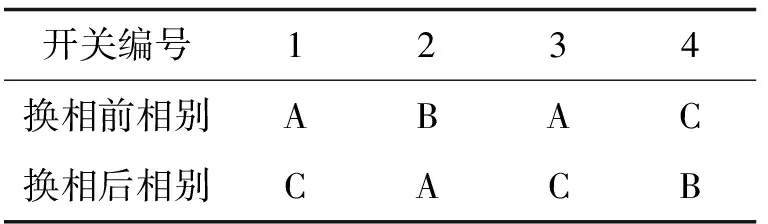
表2 换相前后开关状态分布表

在优化结果上与粒子群算法相比较，开关总动作次数增加了一次，但三相不平衡度大幅降低.从计算速度和迭代结果上来看，改进后的PSO可以使换相策略达到理想水平.同时，在MATLAB软件中使用遗传算法对此低压配电台区负荷进行不平衡情况优化，其中遗传算法参数设置如下： 交叉概率设为0.6，初始变异概率设置为0.02，群体数目为100，迭代次数与粒子群算法的迭代次数相同.各开关换相后的状态矩阵为K4，结果如下：

(16)

由上式可得，换相后A、B、C三相的电流大小分别为97、98、104 A，三相不平衡度为4.39%，但是开关的动作次数达到了9次.与改进前的粒子群算法相比，优化后的不平衡度有所降低，开关的动作次数却更多，与改进后的粒子群算法相比，优化效果不理想.在实现上，遗传算法有“交叉”、“变异”的过程，原理更繁琐，参数更多，实现较为困难，而粒子群算法编程实现更为简单.

此外需要研究的也有对于三相不平衡度和动作次数两者之间的权重函数，由于是多目标优化，二者的权重各不相同，在实际应用中应当结合实际问题加以改变，如果此智能换相开关所应用场合的不平衡问题较为严重，则应当给三相不平衡度函数以更大的权重；若此配电台区不宜频繁地对负荷进行相序转换，则应该在开关总动作次数函数上以较大的权重.

4.3 试验验证

在实验室条件下，搭建三相负荷不平衡模型，进行不平衡负荷条件下的换相试验，验证换相策略的可行性.电源采用可编程交流源，发出220 V，50 Hz的三相交流电.负载采用阻性负载，用滑动变阻器及负载柜，换相开关接在负载前端，进行电量信息采样，接收换相指令，开关动作改变所接入相别.换相前负载的电量信息及相别如表3所示.

根据表中各负载的电流及相别信息，根据式(1)得出试验前的不平衡度为25.81%.使用智能算法对换相策略做寻优迭代计算，得出最佳的换相结果，由换相装置进行相别切换动作.换相结果如表4所示，其中开关动作次数为3次，即有三路负荷发生换相动作.

表3 换相试验前各负荷电流及相别

表4 换相试验后各负荷电流及相别

从表4中可看出，2、4、6号开关相别发生了变化，换相后的不平衡度为6.4%，不平衡度相比较试验之前有较大的降低.三相电流在换相后的波形如图5所示.

通过换相试验前后各相干路上的电流波形可以看出，换相前的三相电流波形大小参差不齐，相差较大，处于不平衡状态，经过换相策略指导的智能换相后，对负荷进行重新分配，使三相电流基本达到幅值大小相同的状态，即处于三相平衡.

试验验证了经过加速粒子群算法迭代计算出的换相方案，通过换相开关作为执行装置，重新调整三相负荷，从而使三相负荷达到平衡状态，降低三相不平衡度.

图5 换相前后三相电流波形Fig.5 Three-phase current waveform before and after commutation

5 结语

在当前低压配电台区具有较为严重的三相不平衡问题，使用智能换相开关能够有效地解决问题，使用MATLAB/Simulink软件搭建模型模拟低压配电台区不均匀分布的负载情况，仿真结果论述了三相负荷不平衡状况下对电网运行造成的不利影响.建立了有关换相策略的两个寻优函数的求解模型，并对基本粒子群算法进行改进，提高寻优性能，同时与改进前的算法迭代计算结果进行比较，对比结果表明，改进后的粒子群算法能够较好地对换相策略进行迭代求解，并具有独到的优势，通过试验验证，证明了改进后的粒子群算法所建立的换相策略在解决三相不平衡问题上的可行性.