基于残差补偿的极限学习机自编码器

陈文坚，陈晓云，汪巧萍

(福州大学数学与统计学院，福建 福州 350108)

0 引言

Huang等[1]提出的极限学习机(extreme learning machine，ELM)面对回归问题时，存在表示能力有限的不足.因此，Zhang等[2]构建残差补偿极限学习机(residual compensation extreme learning machine，RC-ELM)，对回归预测残差进行迭代补偿，来提高回归精度，并通过实验证明了残差补偿思想的有效性.但现实生活中，对标签的标注代价十分昂贵，因此无监督学习方法解决现实问题更为普遍.

Huang等[3]将流形正则的思想引入ELM中，提出无监督极限学习机(unsupervised extreme learning machine，US-ELM)，将原数据投影到低维空间保持其近邻结构不变.Chen等[4]在US-ELM的基础上，提出基于稀疏和近邻保持的极限学习机(SNP-ELM)，保持样本的稀疏性及局部近邻结构不变对数据有较好的自适应性.除了US-SELM，Kasun等[5]将自编码器引入极限学习机中，提出了极限学习机自编码器(extreme learning machine autoencoder，ELM-AE)，目标是重构原始输入，利用输出权重对原始输入进行投影.但对于高维数据，希望提取特征尽量稀疏，因此 Tang等[6]引入l1范数构建极限学习机稀疏自编码器(ELM-SAE)，能够提取更稀疏，更紧凑的输入特征.除此之外，考虑流形结构也是至关重要的，因此Sun等[7]在ELM- AE中引入局部流形结构，提出了广义极限学习机自编码器(GELM-AE)，使得原样本空间中尽量接近的样本，特征映射后在新空间中也能尽量接近.

上述算法都是从近邻结构和稀疏表示改善US-ELM和ELM-AE的表示能力，而残差补偿思想也能改善模型的表示能力，因此本文将残差补偿思想扩展到ELM-AE上，提出了基于残差补偿的极限学习机自编码器(residual compensation extreme learning machine autoencoder，RCELM-AE)，通过对重构残差迭代进行补偿式学习，使重构输出更为接近原始输入，以此改善ELM-AE的表示能力.

1 相关工作

1.1 残差补偿极限学习机

残差补偿极限学习机作为层次结构，由基线ELM和若干补偿ELM组成.基线ELM构建输入数据与预测输出之间的特征映射，补偿ELM对预测残差进行迭代学习，直到没有性能提高或残差小于预定义值为止.

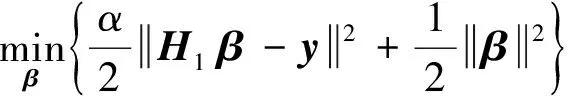
(1)

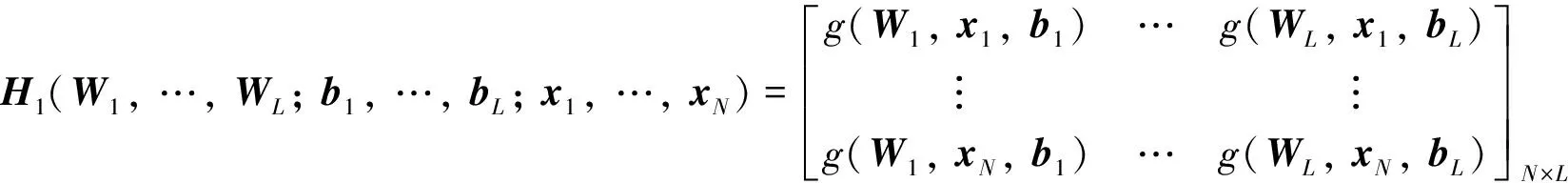
模型第一项为残差项，α为惩罚系数；第二项正则项是为了控制模型复杂度，防止过拟合. 由于只含单一变量β，则该目标函数的解析解如下

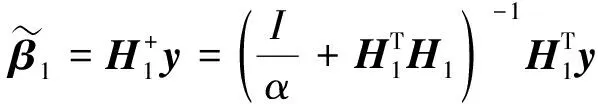
(2)

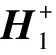
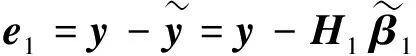
(3)

补偿ELM1以X为输入向量，e1为对应期望目标向量，H2为补偿ELM1的隐层输出，则优化模型如下

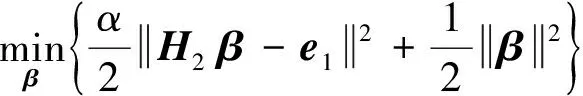
(4)

于是补偿ELM1目标函数的解析解如下

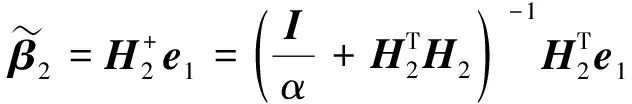
(5)

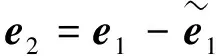
(6)

重复补偿ELM1迭代学习操作，RC-ELM的最终预测值可计算为

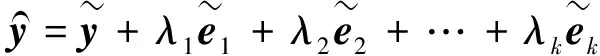
(7)

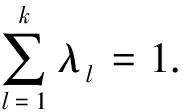
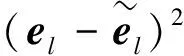
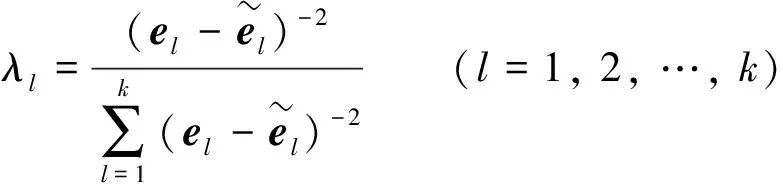
(8)

1.2 极限学习机自编码器

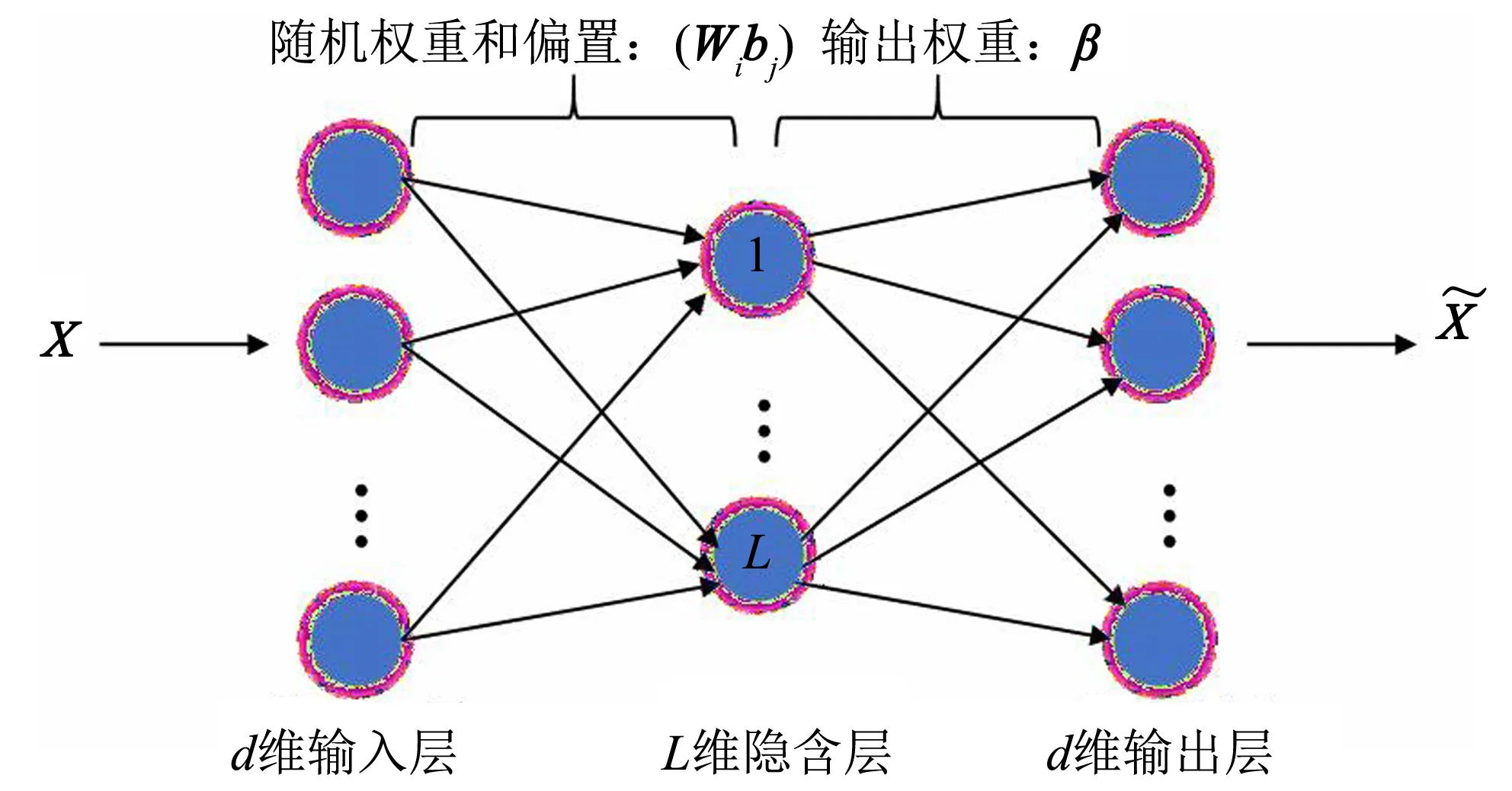
图1 极限学习机自编码器(ELM-AE)的网络结构Fig.1 Extreme learning machine autoencoder(ELM-AE) network structure

极限学习机自编码器(ELM-AE)让输入作为网络理想输出，目的是让输出尽可能等于输入.极限学习机自编码器的网络结构如图1所示.X=[x1,x2, …,xN]T∈N×d为输入向量，Wi和bj如式(1)的构造，是隐层与输出层的权重，N×d为经由ELM-AE映射的重构输出.

ELM-AE从输入层到隐层的操作与ELM一致，两者差别在于ELM隐层到输出层的输出权重β由最小化网络输出Hβ与标签向量y的残差计算得到，而ELM-AE的β是由最小化Hβ与输入样本X的残差计算得到. 则ELM-AE的优化模型如下

s.t.WTW=I，bTb=I

(9)

其中: 当隐层节点个数L小于样本特征维数d时，输入样本可被投影到更低维特征空间. 式(9)求解得到的输出权重β为

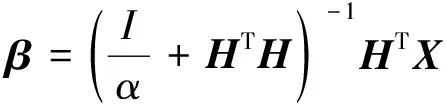
(10)

根据文献[5]，ELM-AE将原始高维样本X与输出权重β相乘进行降维，即可得到降维后样本的新表示Xnew=XβT，可以更有效地应用于数据聚类或分类等任务.

2 残差补偿的极限学习机自编码器

图2 残差补偿极限学习机自编码器 (RCELM-AE)的网络结构Fig.2 Residual compensation extreme learning machine autoencoder(RCELM-AE)network structure

本研究提出残差补偿极限学习机自编码器(RCELM-AE)也是由基线ELM-AE和若干补偿ELM所组成，基线ELM-AE构建输入样本与重构输出之间的映射，补偿ELM对输入样本和重构输出的残差进行迭代学习.RCELM-AE的网络结构如图2所示.

根据式(9)、(10)，求解基线ELM-AE优化模型，可计算出输出权重的解析解：

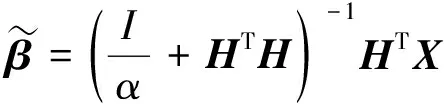
(11)

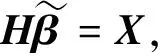
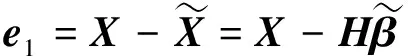
(12)

由于残差中可能蕴含有意义信息，因此进一步用补偿ELM1，补偿ELM2，…, 对e1进行特征表示学习，且设补偿ELMi(i=1, 2, …,k)网络输入和隐层输出均与基线ELM-AE相同，均为X和H.根据式(4)，补偿ELM1的优化模型为

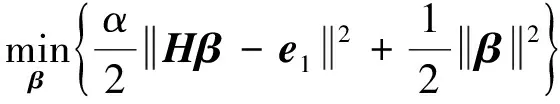
(13)

据式(5)求解补偿ELM1输出权重的解析解

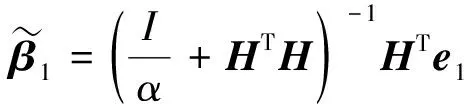
(14)

根据式(8)的启发和(15)，方便H可从多项式中提出来，则权重λl的计算公式如下

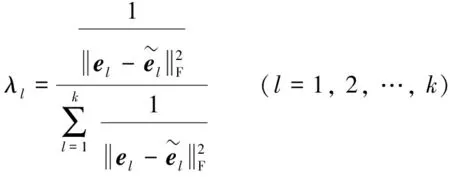
(16)

(17)

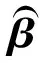
Input: 归一化的数据矩阵X∈ N×d, 隐层节点数(维数)L, 最大补偿层数k, α>0Output: 降维后样本矩阵XnewInitialization: 随机初始化W和b计算隐层输出矩阵H, ε=10-6, l=1. Step1: 通过式(11)和式(12), 计算β和e1Repeat: 通过式(13)和式(14), 计算输出权重βl令el=Hβl, 计算残差el+1=el-el, l=l+1 Until: el+1≤ε or l>kStep2: 通过式(16)和式(17), 计算最终输出权重β(Step3: 计算降维后的样本矩阵Xnew=Xβ(T

基线ELM-AE与补偿ELM的网络结构一致，计算时间开销主要为输出权值的计算, 包括矩阵乘法计算时间复杂度分别O(L2N)、O(LNd)和O(L2d)，矩阵逆的计算时间复杂度为O(L3)，k层补偿ELM的权重计算时间复杂度为O(kd2N)，在本研究的一般情况下隐层节点数量L小于数据样本数量N，两者远小于样本特征维数d，则经过1层基线ELM-AE和k层补偿ELM的RCELM-AE来说，时间复杂度为O((k+1)×(L2N+LNd+L3+L2d)+kd2N)，即O(kd2N).

3 实验结果与讨论

本节验证残差补偿极限学习机RCELM-AE的降维效果, 与5种方法进行降维聚类对比实验，实验基于MATLABR2019b编程实现，实验环境为Win10系统，内存8 GB.实验对比方法包括以下两种:

1) 线性无监督降维方法.主成分分析(principal component analysis，PCA)[9]以最大化投影方差为目标.

2) 无监督极限学习机降维方法.极限学习机自编码器(ELM-AE)，该方法通过将原始输入代替类标签作为网络理想输出; 极限学习机稀疏自编码器(ELM-SAE)，该方法通过l1范数规范输出权重β，使得β稀疏; 广义极限学习机自编码器(GELM-AE)，该方法通过引入流形正则，保持局部近邻结构.

3.1 数据集

对比实验选择6个公开的数据集，分别是2个公开的医学图像数据集，选取BreastMNIST[10]和PneumoniaMNIST[11]；4个基因表达数据集，选取Colon[12]、DLBCL[13]、Prostate0[14]和Leukemia2[15].6个公开数据集的描述如表1所示.

BreastMNIST数据集收集乳腺超声图像，分为正常、良性和恶性3类.并预处理成28 px×28 px图像.PneumoniaMNIST数据集收集胸部X光图像，其中包括肺炎(细菌性肺炎和病毒性肺炎)图像和正常图像.所有的图像如上预处理.两个医学图像数据集部分示例展示如图3.在BreastMNIST数据集中，第1行为正常图片，第2行为良性图片，第3行为恶性图片；在PneumoniaMNIST数据集中，第1行为正常图片，第2、3行为肺炎图片.

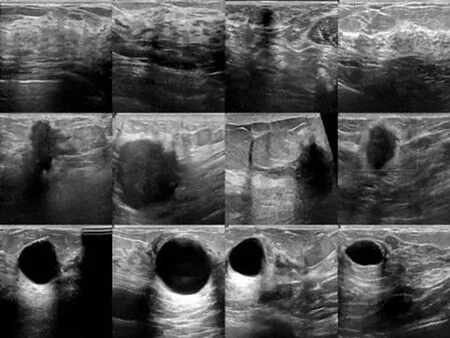
(a) BreastMNIST数据集

(b) PneumoniaMNIST数据集

3.2 参数设置及结果分析

在6个实验数据集上分别采用RCELM-AE与对比方法PCA、ELM-AE、ELM-SAE、GELM-AE进行降维.其中RCELM-AE最大补偿层数k选择5，GELM-AE的近邻数取自5，所有方法选择降维维数搜索范围为{2, 4, 8, …, 64, 100}，参数α和γ搜索范围为{10-3, 10-2, …,103}.

对比实验的5种算法在样本降维之后，都使用K-means 进行聚类，并以聚类准确率进行评估.为减少K-means初始中心的随机性以及ELM-AE随机选取输入权重和偏置带来的影响，实验中ELM-AE，ELM-SAE，GELM-AE和 RCELM-AE分别运行5次，每次降维后执行10次K-means聚类，取50次聚类准确率的平均值作为最终聚类准确率，PCA将10次K-means聚类的聚类准确率平均值作为最终聚类准确率.所有方法在6个实验数据集的最佳聚类准确率均值和方差(运行时间，降维维数)列于表2，其中降维维数为每个数据集最优聚类结果对应的降维维数，运行时间为每个数据集最优聚类结果的模型运行时间(s).

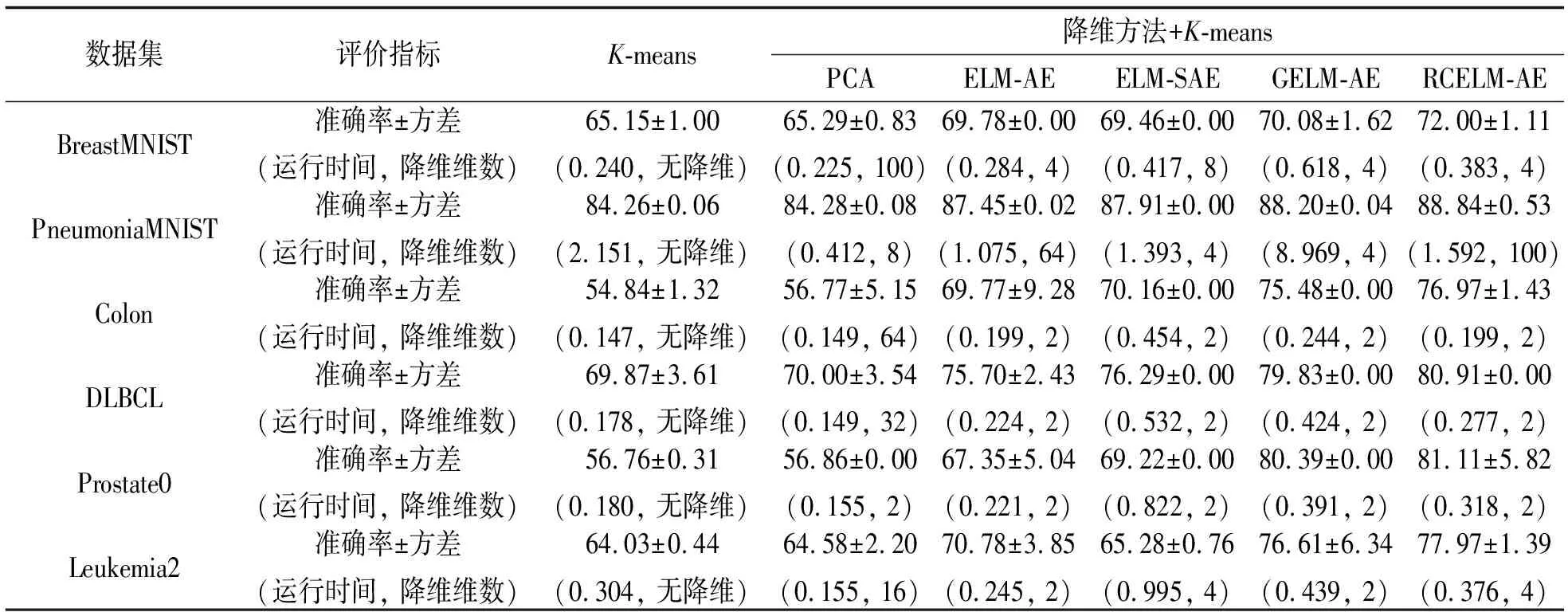
表2 聚类准确率

从表2可以看出，RCELM-AE 的聚类准确率在6个数据集中都是最优的.RCELM-AE聚类准确率比ELM-AE有大幅度提高，提高幅度1.39%～13.76%，这说明RCELM-AE通过残差补偿能够得到更接近原始样本的重构输出，进而使得输出权重β更好表示原始样本，运行时间略有提高，这是因为RCELM-AE增加残差补偿，说明RCELM-AE小幅度提高运行时间可得到比ELM-AE更优的聚类准确率.RCELM-AE准确率比ELM-SAE有提高，提高幅度0.81%～12.69%，这说明残差补偿得到的β比l1范数规范的β更能表示原始样本，ELM-SAE运行时间比RCELM-AE平均提高0.9倍，这是因为ELM-SAE要求解l1范数，说明除了PneumoniaMNIST 数据集，RCELM-AE在运行时间和聚类效果都优于ELM-SAE.RCELM-AE聚类准确率比GELM-AE略有提高，提高幅度0.64%～1.92%，说明残差补偿思想比流形正则项聚类效果略好，GELM-AE运行时间比RCELM-AE平均提高1.1倍，这是因为GELM-AE要计算拉普拉斯矩阵，说明RCELM-AE运行效率优于GELM-AE.另外，GELM-AE对于PneumoniaMNIST数据集的时间复杂度非常大，说明GELM-AE不适合大型数据集.

3.3 参数影响

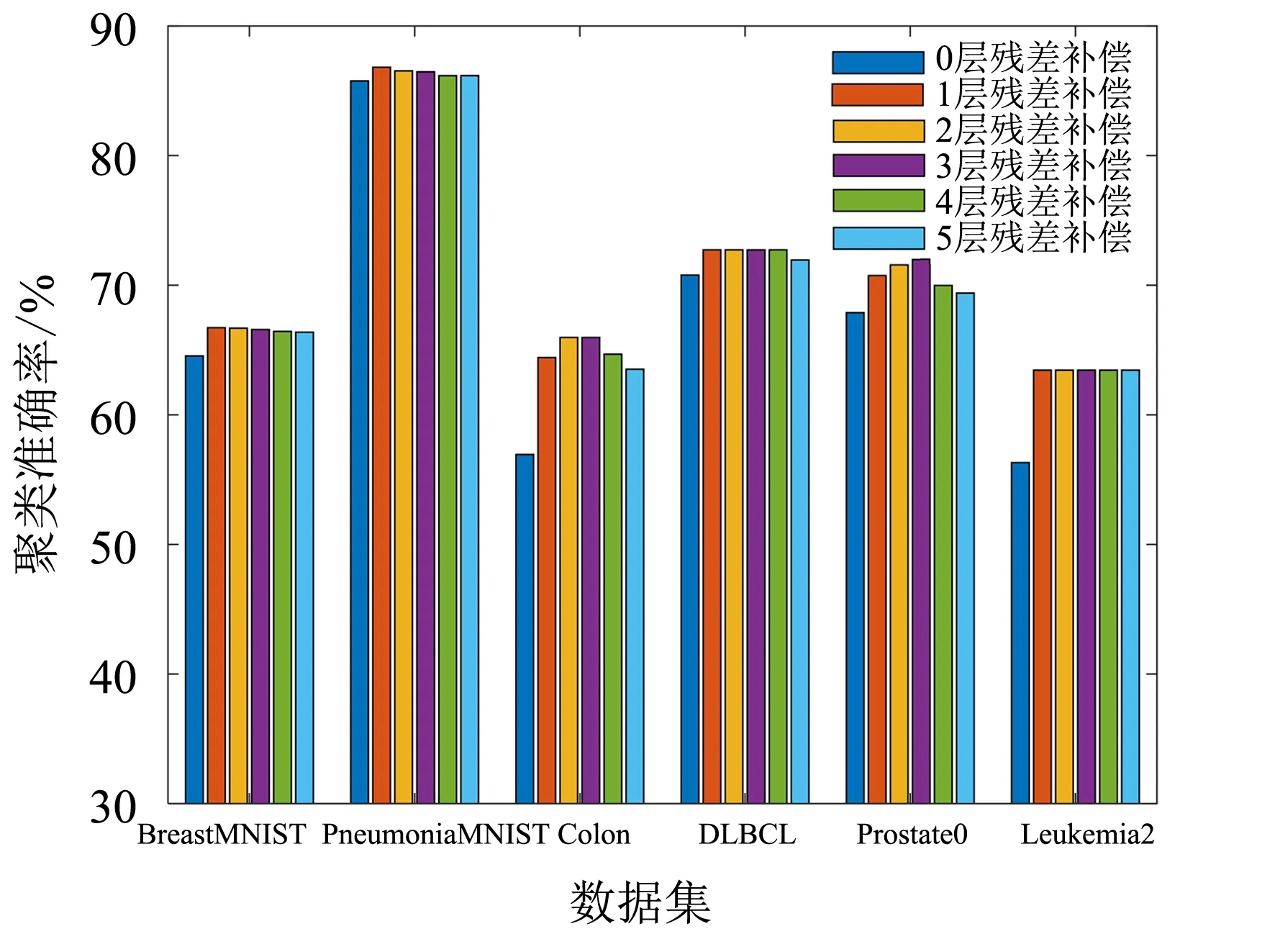
图4 不同残差补偿次数的聚类准确率Fig.4 Ariation of clustering accuracy with respect of residual compensation times

RCELM-AE其中一个参数l，代表补偿ELM的层数.通过不同数据集结构，分析残差补偿层数对聚类准确率的影响，如图4所示.从图4可以看出，0层残差补偿为经典ELM-AE，所有数据集1层残差补偿的聚类效果都比0层残差补偿要好，这说明残差补偿确实有益于表示学习.2个医学图像数据集DLBCL和Leukemia2在1层残差补偿下就能获得较高的聚类准确率，而Colon和Prostate0则是在2或3层残差补偿下获得较高聚类准确率，这说明RCELM-AE在1～3层残差补偿下就能达到较高的聚类准确率.

除了残差补偿层数影响RCELM-AE的聚类准确率，RCELM-AE有两个需要优化的参数，分别是隐层维数L和惩罚系数α.而从表2和图4可知，RCELM-AE降维维数为2和残差补偿层数为1时，聚类准确率能达到较好的结果，因此只需对惩罚系数α进行分析，并且固定隐层维数L为2和残差补偿层数l为1.

图5给出RCELM-AE在医学图像数据集和基因表达数据集的聚类准确率随参数α不同取值的变化情况.从图5(a)中可以看出，2个医学图像数据集从α=10-3到α=1之间聚类准确率有提高趋势，并在α=1时聚类准确率达到最高，之后呈下降趋势，说明在2个医学图像中模型正则项和残差项起到相同主导作用；而从图5(b)中看出，Colon从α=10-2到α=10-1时聚类准确率有略微提高，之后便下降直至平稳，其余3个基因表达数据集在α=10-3时聚类准确率开始下降直至平稳，因此大部分基因表达数据集在α=10-3取得最高聚类准确率，只有Colon在α=10-1比α=10-3聚类准确率略微提高，说明基因表达数据集α取较小值时RCELM-AE能达到较好效果，表示此时模型起到主导作用是正则项.总体而言，随着数据集特征维度的增加，达到最优聚类准确率所选取的α则越来越小.

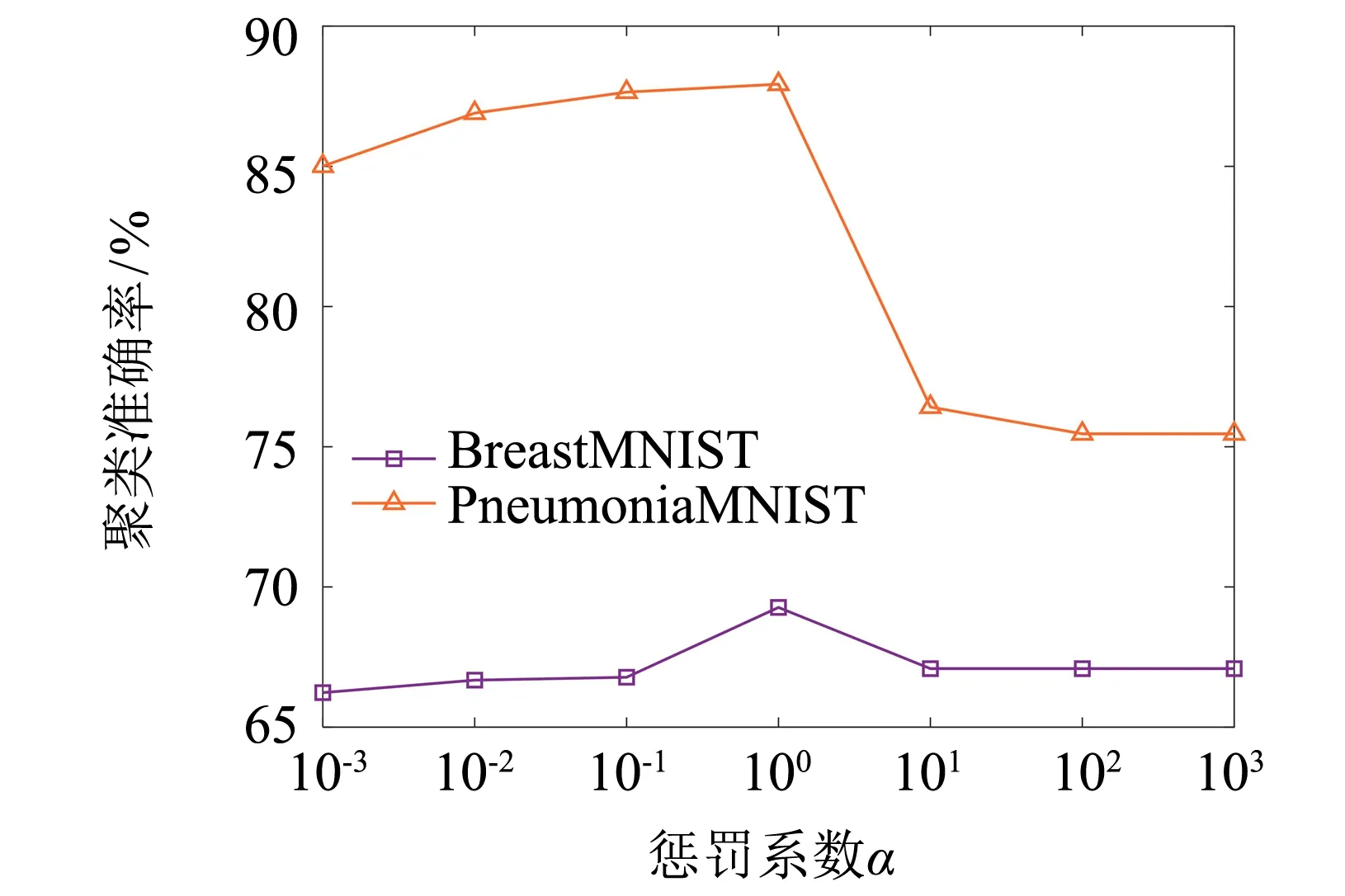
(a) 医学图像数据集

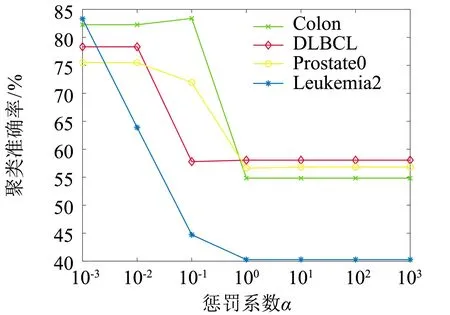
(b)基因表达数据集

3.4 抗噪对比实验

由于现实生活的数据有可能包含噪声，使得残差中可能存在噪声，为验证RCELM-AE对噪声数据的鲁棒性，选择BreastMNIST和PneumoniaMNIST这两个医学图像数据集，并在图像样本中叠加高斯白噪声和椒盐噪声.高斯白噪声[16]生成公式如下：

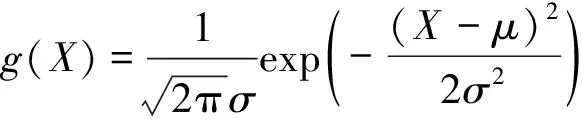
(18)

其中：μ为高斯分布的均值；σ为高斯分布的方差，生成的高斯白噪声叠加在原始图像.

椒盐噪声[17]生成公式如下：

(19)

其中:smin为原始图像所有灰度级中最小值;smax为原始图像所有灰度级中最大值;xi, j表示第(i,j)像素位置的灰度级，r=p+q代表了噪声级，最终生成椒盐噪声图像.

本文6个方法的抗噪对比实验，选择原始数据，方差为0.002的零均值高斯白噪声数据和噪声级为0.02的椒盐噪声数据，实验结果列于表3.

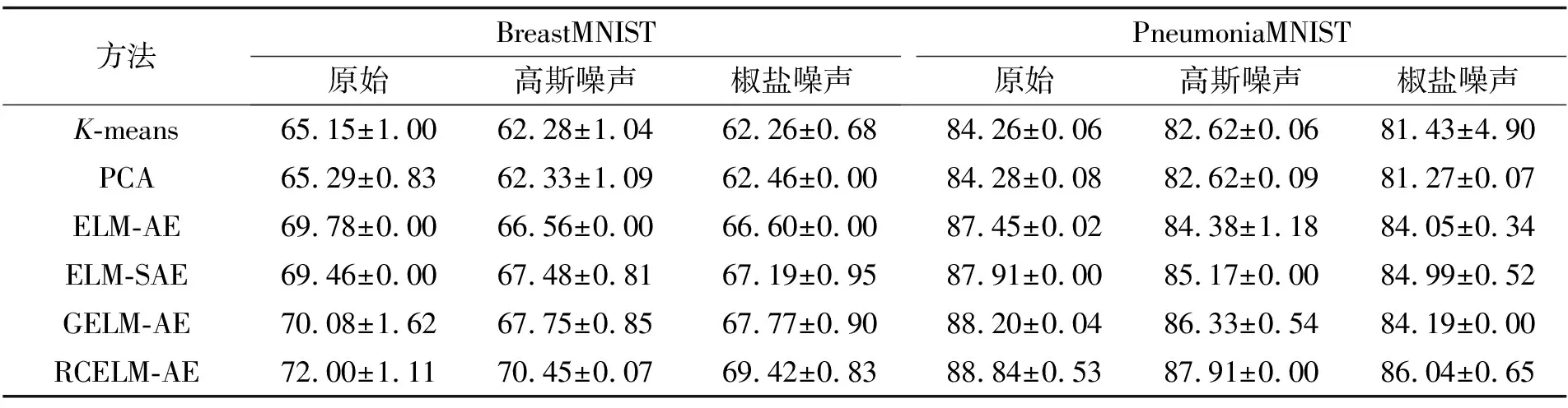
表3 混合噪声对比实验的聚类准确率

从表3中可以看出，无论增加高斯白噪声还是椒盐噪声，6种方法的聚类准确率都随之下降，但2个数据集中RCELM-AE的聚类准确率依旧最高，且RCELM-AE的下降幅度很小.说明, 无论是高斯白噪声还是椒盐噪声，RCELM-AE抗噪性能方面都排在前列，具有较好的鲁棒性.

4 结语

在ELM-AE模型基础上，提出基于残差补偿的极限学习机自编码RCELM-AE.通过对重构残差补偿式学习，来改善基线ELM-AE表示学习能力.在 6个公开数据集上降维后的聚类实验结果表明，RCELM-AE的聚类准确率优于PCA和无监督极限学习机降维方法，而且也不会带来过高的时间复杂度，抗噪实验结果表明RCELM-AE具有较好鲁棒性.