投影自表示无监督极限学习机

汪巧萍，陈晓云

(福州大学数学与统计学院，福建 福州 350108)

0 引言

子空间聚类是数据聚类的有效方法之一，在计算机视觉、机器学习等领域引起了广泛的关注.对高维数据进行子空间聚类时，主要存在以下两个问题： 1) 高维数据中存在大量无关的属性使样本中存在簇的可能性很小；2) 高维空间中数据分布稀疏，刻画样本间相似度困难.因此, 研究面向聚类任务的降维方法是必要的.典型的线性降维方法有： 主成分分析[1](以最大化投影散度为目标)、局部保持投影[2]、近邻保持嵌入[3](以保持原数据近邻结构为目标降维).当数据非线性分布时，上述线性降维算法无法有效提取特征.

无监督极限学习机(unsupervised extreme learning machine，US-ELM)和极限学习机自编码器(extreme learning machine auto-encoder，ELM-AE )是两类典型的非线性降维方法.无监督极限学习机如US-ELM[4]和SNP-ELM[5]，US-ELM通过投影后样本的近邻结构保持不变实现降维；SNP-ELM通过投影后的样本同时保持样本的稀疏性和局部近邻不变学习投影矩阵.极限学习机自编码器如ELM-AE[6]、GELM-AE[7]，ELM-AE引入自编码器的思想，网络输出和输入保持不变为目标学习降维投影矩阵；GELM-AE在ELM-AE的基础上引入局部流形思想，保持数据全局和局部结构实现降维.

上述极限学习机方法基于全局或局部保持不变的思想进行降维，但是忽视了样本集所特有的簇类子空间结构信息.本研究在US-ELM基础上引入子空间聚类的自表示模型[8]，提出投影自表示无监督极限学习机(projected self-expressive unsupervised extreme learning machine，PS-ELM)模型.PS-ELM同时学习降维投影矩阵β和投影后样本的自表示矩阵Z，通过交替迭代更新β和Z，可提取更加有效的低维特征和更接近数据本质特征的自表示矩阵.

1 无监督极限学习机

无监督极限学习机US-ELM是单隐含层前馈神经网络，第一过程先将输入数据映射到r维(r是隐含层节点数)特征空间中. 给定数据矩阵X=[x1,x2, …,xn]∈Rm×n，m是样本的维度，n是样本数目，H(xi)=[g(w1,b1,xi),g(w2,b2,xi), …,g(wr,br,xi)]T∈Rr，输入数据映射到r维的特征空间H(xi). 其中g为激活函数，如Sigmoid函数. 权重w和偏置b随机初始化，则X在隐含层输出为：

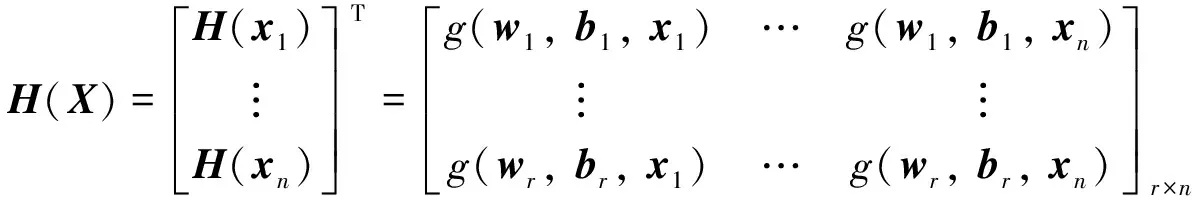
(1)

第二过程是求解输出权重矩阵β∈Rd×r，d是样本投影后的维度，样本xi经过US-ELM输出为yi=βH(xi)∈Rd. US-ELM隐含层向输出层投影时对原始空间中距离相近的样本点加大惩罚使得投影后样本仍保持近邻关系，最小化目标函数如下:

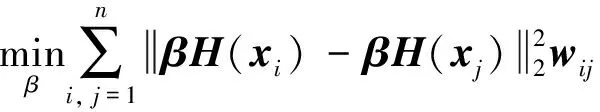
(2)

其中:wij表示样本xi和样本xj的相似度.wij定义如下：

(3)

这里，Nk(xi)为样本xi在原空间中的k近邻集合. 经过代数运算得到US-ELM目标函数为：

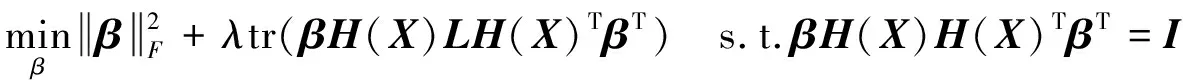
(4)

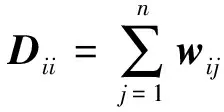
(I+λH(X)LH(X)T)v=θH(X)H(X)Tv

(5)

2 投影自表示无监督极限学习机

2.1 基于自表示学习的子空间聚类

给定原始样本数据矩阵X∈Rm×n，m为样本的维数，n为样本数目. 基于自表示学习的子空间聚类模型的基本框架为：

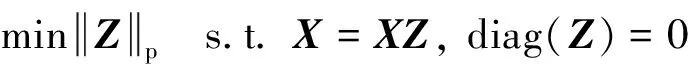
(6)

其中：Z∈Rn×n是自表示矩阵，可用来衡量样本间的相似度，对角阵为0的约束是为了避免平凡解即样本被自身完全表示. 对Z的范数约束常用l1范数[9]、核范数[10]、Frobenius范数[11]. 在实际生活中, 数据往往含有噪声, 因此松弛式(6)得：

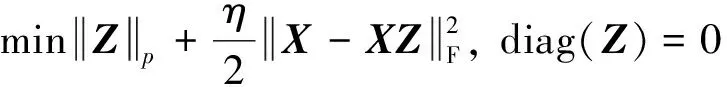
(7)

2.2 投影自表示无监督极限学习机模型

由于高维数据存在一定的冗余信息，导致自表示矩阵不能刻画数据之间的本质关系.SNP-ELM保持高维数据中的稀疏性和近邻表示，但是在低维空间中这两种结构不一定保持.针对上面的问题，本研究提出投影自表示无监督极限学习机(PS-ELM)模型.在投影过程中引入自表示模型指导学习投影矩阵β，反过来投影后的样本特征用于学习样本间的自表示矩阵Z，从而有利于子空间聚类，具体模型如下：

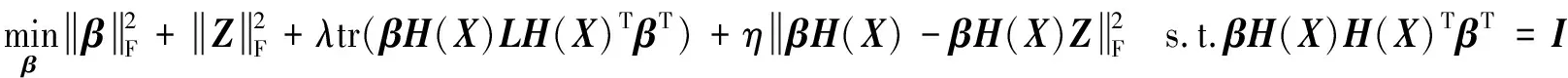
(8)

这里，λ和η是平衡参数. 第一项是控制模型复杂度的正则项，第二项约束自表示矩阵Z块对角结构，第三项使投影后的样本保持数据局部流形结构，第四项是投影样本的自表示误差，为了避免平凡解，算法加入正交约束βH(X)H(X)TβT=I.PS-ELM模型的网络结构如图1所示，Y是投影后的特征空间，Z是Y的自表示矩阵，两个过程联合优化，使得投影和子空间聚类任务相互适应. 目标函数有两个变量β和Z，为求解模型，采用交替迭代二乘法ALS[12]进行求解.

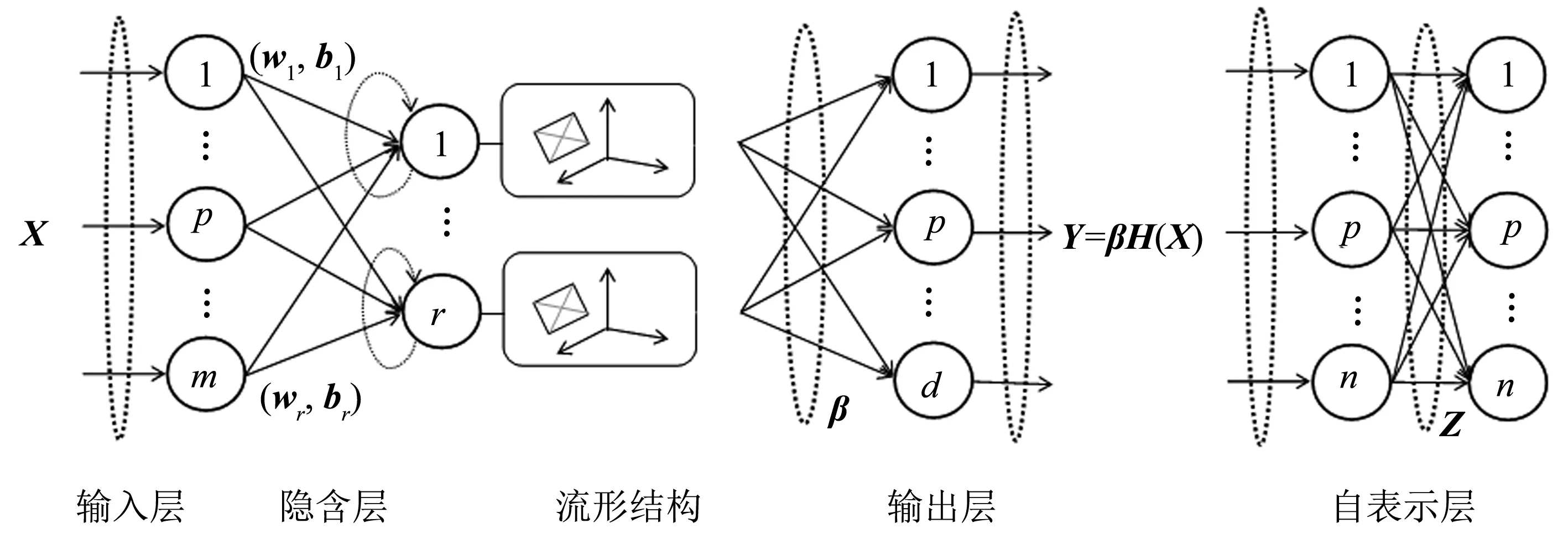
图1 投影自表示无监督极限学习机结构图Fig.1 The network structure of projected self-expressive unsupervised extreme learning machine

首先固定Z，使得投影样本保持子空间结构Z求解投影矩阵β，则模型(8)可以转化为：

(9)

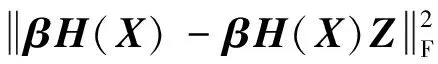
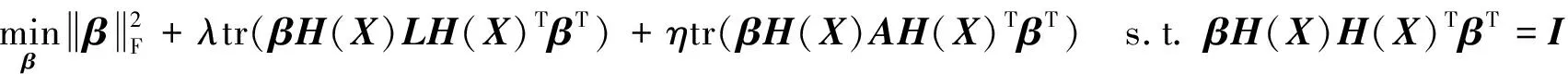
(10)

为求解模型(10)，利用拉格朗日乘子法得到以下拉格朗日函数：

L(β)=tr(βTβ)+λtr(βH(X)LH(X)TβT)+ηtr(βH(X)AH(X)TβT)+

θtr(βH(X)H(X)TβT-I)

(11)

这里:θ是拉格朗日参数令∂L/∂β=0得：

(I+λH(X)LH(X)T+ηH(X)AH(X)T)βT=θH(X)H(X)TβT

(12)

求解关于矩阵M=I+λH(X)LH(X)T+ηH(X)AH(X)T和矩阵N=H(X)H(X)T的广义特征值问题(12)得到最小的d个特征值及对应的特征向量构成输出权重矩阵β.

当r>n时，H(X)H(X)T∈Rr×r的维数较高，直接求解式(12)的广义特征值问题的计算复杂度较高. 根据文献[13]的方法, 可令β=αTH(X)T, 式(11)两边同时左乘(H(X)TH(X))-1H(X)T得到：

(I+λLH(X)T(X)+ηAH(X)TH(X))α=θH(X)TH(X)α

(13)

因此解得广义特征值问题(13)的最小的d个特征值及对应的特征向量构成矩阵α，从而可得模型(12)的解β=αTH(X)T.

其次固定投影矩阵β，利用样本的低维表示βH(X)指导学习子空间自表示矩阵Z，目标函数如下：

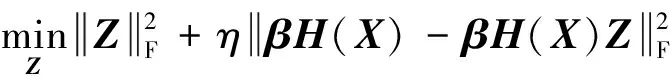
(14)

目标函数(14)关于Z的拉格朗日函数为：

L(Z)=tr(ZTZ)+ηtr(βH(X)AH(X)TβT)

(15)

令∂L/∂Z=0，可以得到：

Z=(I+ηH(X)TβTβH(X))-1H(X)TβTβH(X)

(16)

综上分析，投影自表示无监督极限学习机PS-ELM算法如下：

PS-ELM算法Input: 数据集X∈Rm×n, 平衡参数参数λ, η, 和最大迭代次数maxiter.Output: 降维后样本矩阵Y=βH(X), 自表示矩阵Z, 聚类结果.Initialization: 随机初始化w和b, 并计算隐含层输出矩阵H(X), ε=10-5, iter=1, 利用最小二乘子空间聚类LSR计算原始数据X的自表示矩阵Z, 利用式(3)计算样本之间的相似度矩阵W.Step 1: Repeat: if rmaxiter.Step2: 应用谱聚类N-Cuts算法对邻接矩阵Z∗=(Z+ZT)进行分割.Step 3: 对降维后的样本矩阵Y=βH(X)∈Rd×n应用k-means聚类.

PS-ELM算法计算k近邻图的时间复杂度为O(n2)；求解自表示矩阵Z的复杂度为O(n2r)；求解投影矩阵β时若求解广义特征值式(12)，则其时间复杂度为O(r3)，若求解广义特征值式(13)的时间复杂度为O(n3)，则总的时间复杂度为O(n3+n2r).

3 实验结果与分析

PS-ELM是面向聚类的降维方法，本研究设计两个实验，分别是数据降维的二维可视化和面向聚类的高维数据降维实验.实验基于MATLABR2016a编程实现，实验环境为Win7系统，内存8 GB.ELM-AE、US-ELM、SNP-ELM和本研究方法PS-ELM均采用sigmoid激活函数，其中US-ELM、SNP-ELM、PS-ELM的近邻数k和隐含层节点个数r分别设置为5和1 000，正则参数取值范围为{10-4, 10-3, 0.5×10-3, 10-2, 0.5×10-2, 0.5×10-1, 10-1, 1, 5, 101, 102, 103}.

3.1 数据可视化实验

IRIS数据集由三种鸢尾花组成，每个样本有4个维度的特征.分别用ELM-AE、US-ELM、SNP-ELM和本研究方法PS-ELM将IRIS数据集投影到2维空间，直观地展示低维投影.4种算法分别选取聚类准确率最好的降维结果进行展示，可视化结果如图2所示.从图2中看出上述几种降维方法能够将以蓝色为代表的一类样本较好地分离，而第二类和第三类样本仍少部分重叠.其中US-ELM和ELM-AE投影得较为分散，簇类聚集性不高.SNP-ELM保持原始数据的稀疏性和局部近邻不变，因而能够比较好地将同类样本聚集在一起.本研究提出的PS-ELM算法面向子空间聚类进行降维，学习投影后样本的子空间结构，使得降维后同类样本聚集性最高，而类间样本的距离较大，有利于聚类.

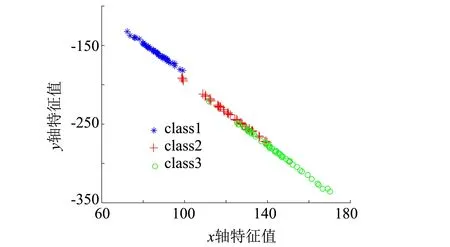
(a) ELM-AE

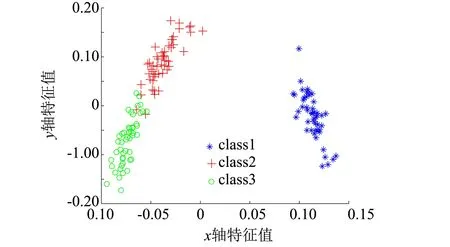
(b) US-ELM

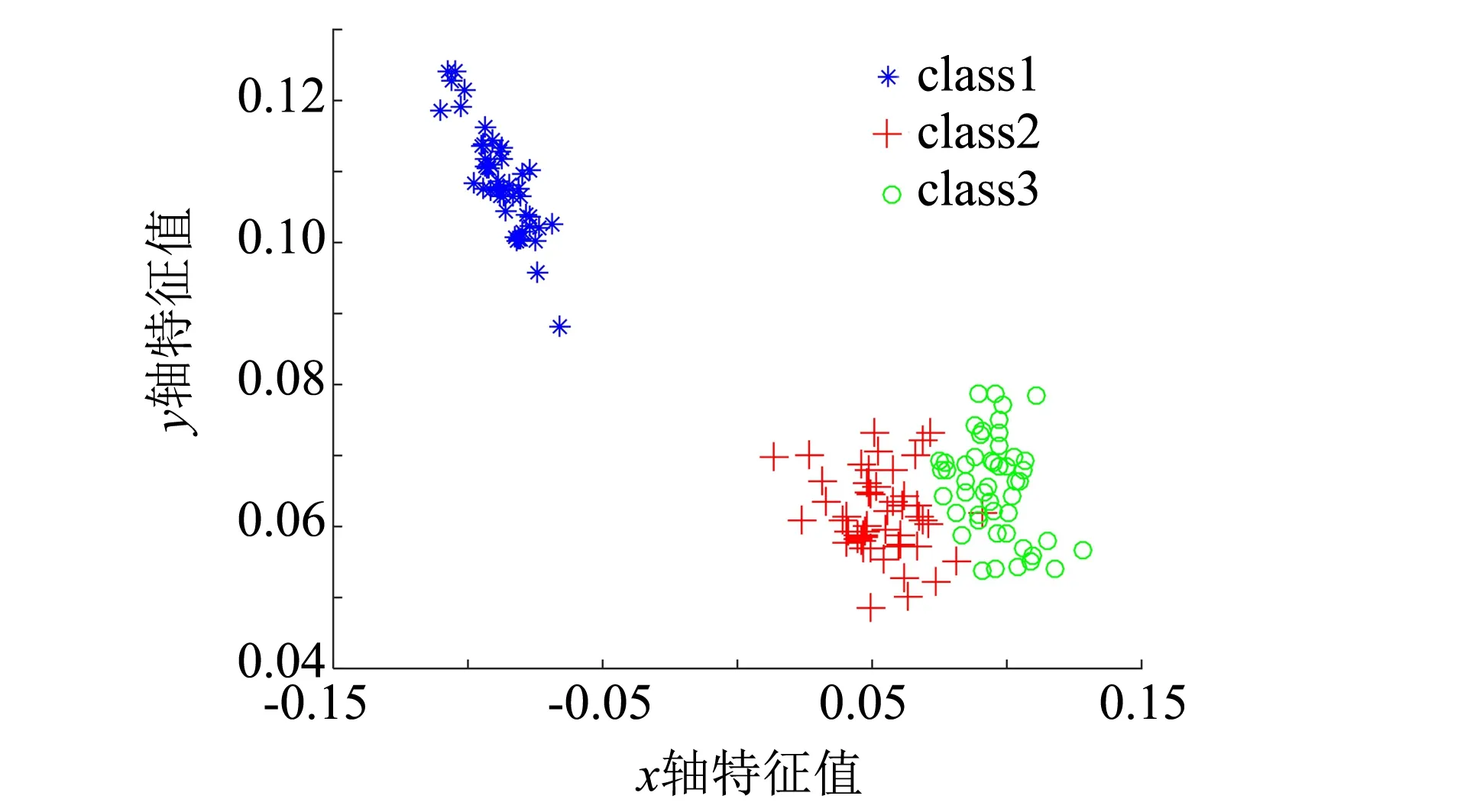
(c) SNP-ELM

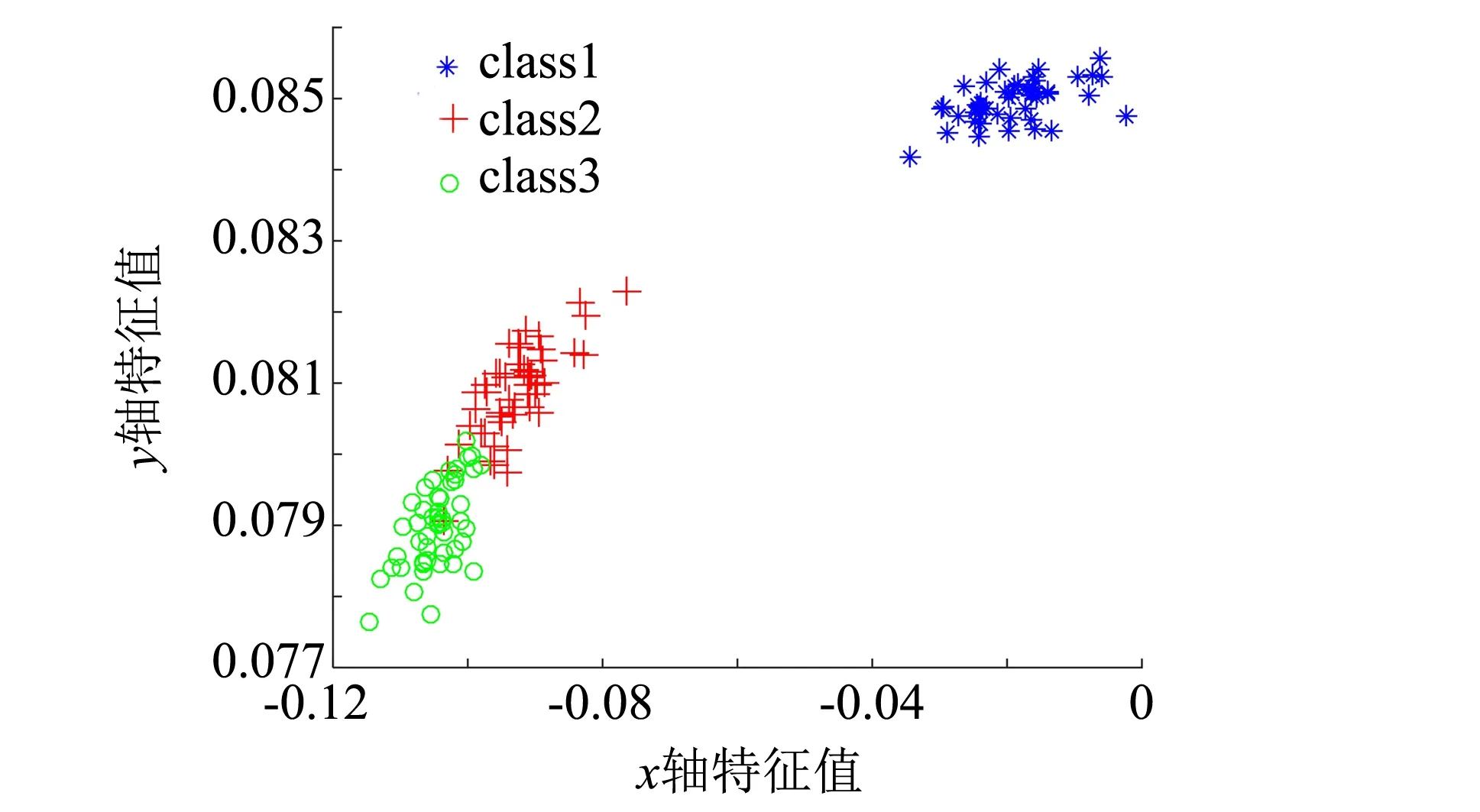
(d) PS-ELM

3.2 聚类实验

图3 2个医学图像数据集部分示例图Fig.3 Partial examples of two medical image data sets

实验采用6个高维基因表达数据集，2个医学图像数据集BreastMNIST[14]和PneumoniaMNIST[15]验证所提方法面向聚类任务的有效性.BreastMNIST数据集收集了年龄在25岁到75岁之间女性的乳腺超声图像，正常和良性图像作为阴性，恶性图像作为阳性.PneumoniaMNIST数据集收集了儿童的胸部X光图像，包括肺炎(细菌性和病毒性肺炎)图像和正常图像，实验随机选取其中的1 000张图像.2个医学图像数据集部分示例展示如图3.8个数据集的描述在表1，所有的实验数据集都经过统一的标准化处理.以投影样本的聚类准确率衡量降维质量，聚类准确率(accuracy, ACC)[16]计算公式为：

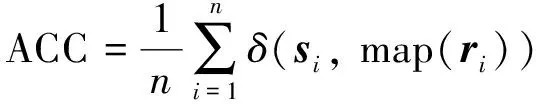
(17)

其中：n为样本数;si和ri为真实标签和预测标签; map(·)将聚类得到的类标签映射成与真实类标签等价的类标签, 当si=map(ri)时，δ(si, map(ri))=1，否则等于0 .

表1 数据集描述

PS-ELM方法求解得到β和Z后有两种方式求解聚类结果，一是用k-means对降维后的样本进行聚类，二是利用谱聚类对自表示矩阵Z进行分割.故实验选取US-ELM、ELM-AE、SNP-ELM将样本投影到{21, 22, 23, …, 2n}维用k-means聚类进行寻优并进行对比.同时选取文献[8]中的投影最小二乘子空间(projection least square regression, PLSR)和投影低秩表示(projection low rank representation, PLRR)进行对比，对投影过程中学习的自表示矩阵Z执行N-cuts聚类.所有算法在每个数据集遵循参数寻优方法，并执行10次实验取聚类准确率的均值和标准差，实验结果如表2所示.

表2 八个数据集上的聚类准确率对比

从表2可以得出以下几点结论：

1) ELM-AE仅保持自身的全局结构，相对于保持局部流形的US-ELM的聚类准确低.本研究提出的PS-ELM方法在US-ELM基础上引入自表示模型，在投影过程中学习子空间结构适应于谱聚类，反过来子空间结构指导学习投影矩阵，聚类准确率得到大大提升.

2) SNP-ELM保持的原始高维数据的稀疏和局部近邻结构不一定适应于低维空间.而本研究方法PS-ELM在投影过程中自适应学习子空间结构，除了在PneumoniaMNIST数据集用k-means聚类比SNP-ELM低0.5%，在其他数据集上的聚类准确率比SNP-ELM高.

3) PLRR和PLSR在子空间聚类模型中引入线性投影矩阵，降维过程中同时学习自表示矩阵，然而线性投影方法只能提取高维数据的线性特征，而本研究方法PS-ELM可以提取非线性的特征，经过多个数据集的对比，PS-ELM聚类准确率提高1.20%～24.3%.

4) PS-ELM在6个高维基因数据集上的提升范围为0.79%～35.35%，而针对样本数目较多、医学背景复杂的2个医学影像数据集提升范围在2.39%～12.38%.对比PS-ELM的两种聚类方式，用自表示矩阵Z执行谱聚类的效果比投影样本执行k-means聚类更理想，证明了本研究所提方法是一种有效的面向子空间聚类的非线性投影算法.

3.3 参数分析

PS-ELM方法有2个正则参数λ和η，分别用来平衡流形正则项和子空间自表示误差项，以LEUKEMIA1和DLBCL数据集为例，选取最优的投影维度d并讨论这两个参数对最终实验聚类准确率的影响.

从图4可以看出，当λ值在0.001～1.000之间，η取值在0.01～10.00之间时，PS-ELM方法的聚类效果更好.总的来说，对高维数据而言，λ和η取值较小时本研究方法能达到较好效果.

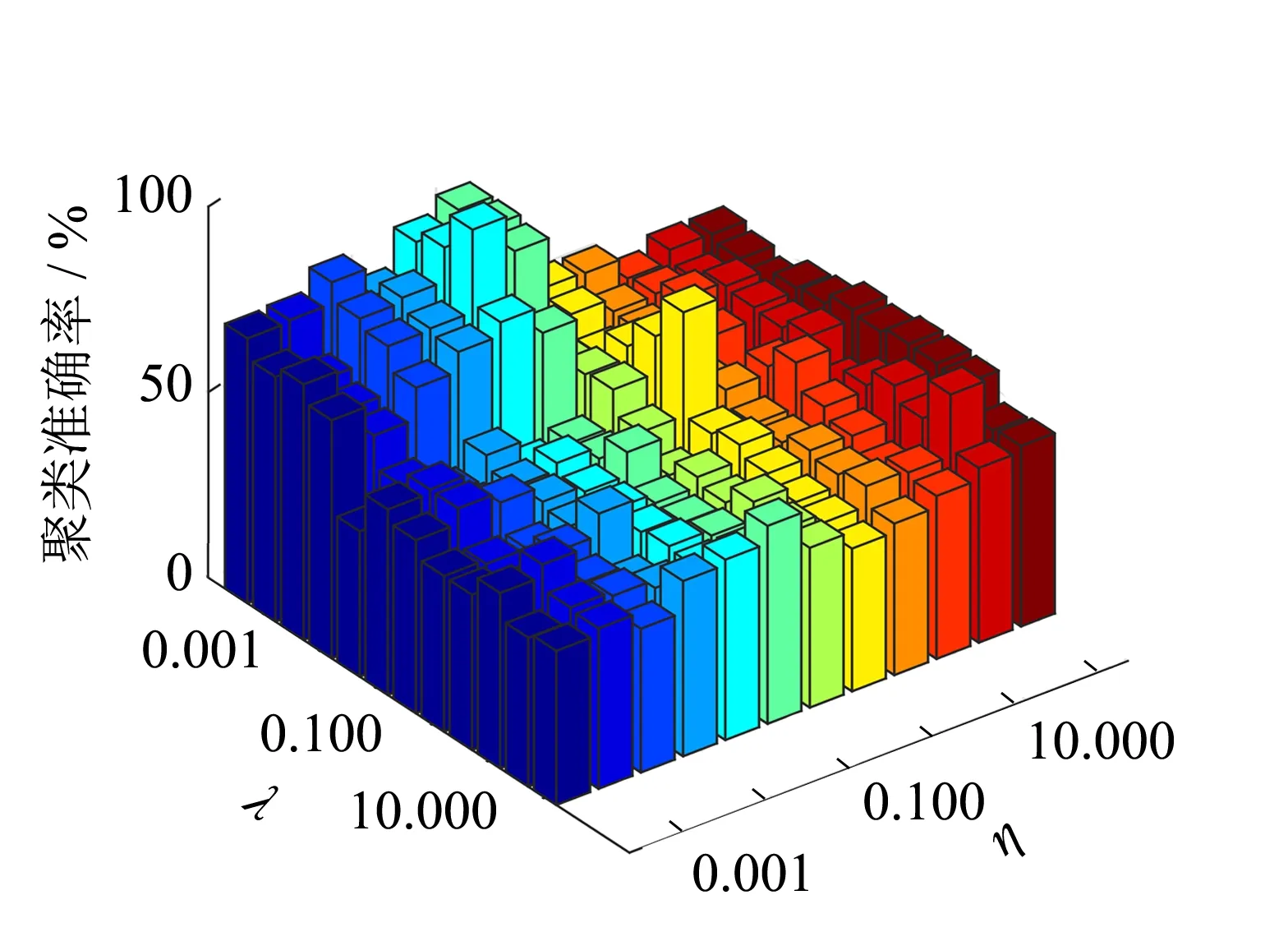
(a) LEUKEMIA1

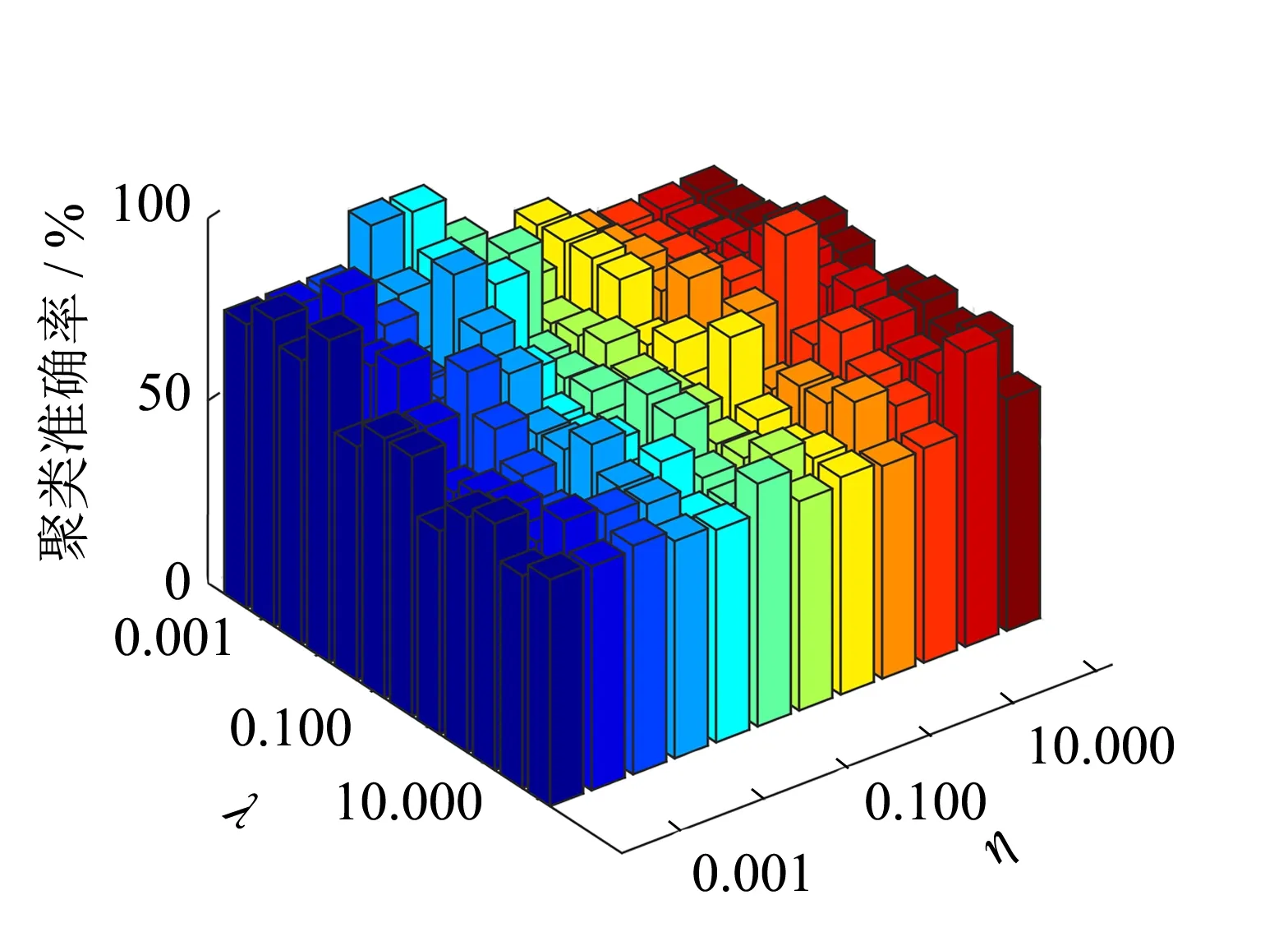
(b) DLBCL

4 结论

本研究提出投影自表示无监督极限学习机PS-ELM方法，通过优化学习自表示矩阵和无监督极限学习机的投影矩阵，不仅保持了原有数据的局部流形结构，且投影过程中自适应地学习子空间结构，较好地适应子空间聚类.实验结果表明在高维的基因表达数据集和医学图像数据集上表现突出，算法的性能优于其他面向聚类的降维方法.