车载超级电容系统的RBF神经网络自适应鲁棒滑模控制方法

王晓侃，王琼

（1 北京交通大学电子信息工程学院，北京 100044；2 河南机电职业学院，新郑 451191）

城市轨道交通运量大、速度快、准时、全天候有效地缓解了城市交通堵塞和拥挤的问题，推进了城市的现代化进程.据统计，城市轨道交通已经发展到300多个城市和国家，部分地区城轨客运量已经占到了50%~80%.截至2021年6月30日，中国内地有40个城市开通地铁线路，累计运营线路长度6641.73 km，已经进入一个高速发展的黄金期.

轨道交通通常站间距比较短、运行密度比较高，列车不停地启动和制动，在此过程预计会产生大量制动能量，可以占到牵引能量的30%~45%［1-4］.通常这部分能量通过电阻直接以热量的形式消耗掉，得不到利用，同时会影响牵引系统的电压变化，为此，引入车载储能系统进行能量回收和利用［5，6］，车载储能服系统是一个非线性特性较为严重、系统参数具有不确定性的系统，而且存在外界干扰和耦合扰动等，使得对车载储能系统进行精确控制具有较大难度.

本研究设计的基于超级电容的车载储能控制系统是一类非线性不确定控制系统，而且存在外界干扰和耦合扰动影响，不容易对该系统进行精确控制和节能研究分析.ADIB等［7］提出一种基于DC-DC和电池的复合车载超级电容系统进行能量回收和利用，GAO等［8］提出了一种基于超级电容器（SC）的地铁网再生制动能量存储系统，SHETTY等［9］提出了一种基于人工神经网络和滑模控制的制动力优化分配问题的求解方法，MA等［10］设计了由径向基函数（RBF）神经网络和滑模控制器（SMC）组成的控制器进行电动汽车制动过程中回收能量，以延长行驶距离和节能.MAO等［11］针对汽车防抱死制动系统对制动过程必须快速、鲁棒的要求，设计了一种基于RBF神经网络的滑模控制器.HUNG等［12］提出了一种基于解耦方法的自适应神经网络滑模控制器设计方法对对车杆系统和球梁系统进行了仿真.但滑模控制在设计实际控制系统中，容易在滑模面两侧产生抖振.为了有效地缓解传统滑模控制中常见的控制抖振问题，从一定程度上提高神经网络自适应控制系统的鲁棒性，本研究结合RBF神经网络具有优秀的非线性函数逼近、自适应和自学习能力等优点，滑模控制可以通过控制量的切换使系统沿着滑模面滑动使系统具有很好的鲁棒性和抗干扰性，且该算法与系统的参数摄入和扰动无关，因此可以考虑使用滑模控制进行车载超级电容系统控制.因此，提出一种车载超级电容RBF神经网络自适应鲁棒滑模控制方法，可以实现列车再生制动能量的循环利用，同时减小牵引网线路损耗.

1 基于超级电容的城轨列车车载能量控制系统

结合城轨列车运行特性和能量利用情况，设计了一种基于超级电容的城轨列车车载能量控制系统如图1所示.

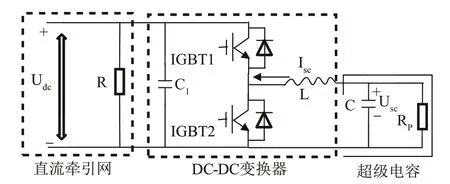
图1 一种车载超级电容能量控制系统结构图Fig.1 Structure diagram of an on-board super capacitor energy control system

（1）仿射非线性充放电模型建立.

根据车载超级电容控制系统的工作模式，若列车启动或者加速时，为避免给列车提供电能导致电网电压的跌落，列车制动和减速运行状态时或电网电压有提升时，能量系统处于充电状态；列车加速时或电网电压有下降时，能量系统处于放电状态.采用状态空间平均法进行电路建模可得到放电状态和充电状态的下模型［13］如下：

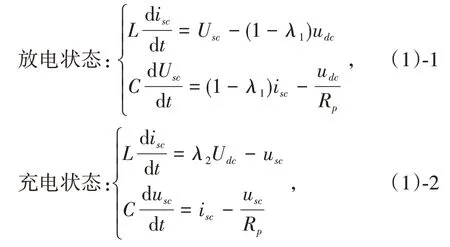
其中，L为储能系统电路中有效电感值；C为超级电容组等效值；Rp为等效负载阻值；λ1、λ2分别为IG⁃BT1和IGBT2的占空比，Isc为1个开关周期的等效电感平均电流值，isc为瞬时值，Usc为1个开关周期内的电容两端电压的平均值；Udc为列车运行时牵引网电压.

假设x1=isc，x2=Udc，可以得到车载超级电容储能系统的一类二阶非线性不确定仿射系统为：

其中：

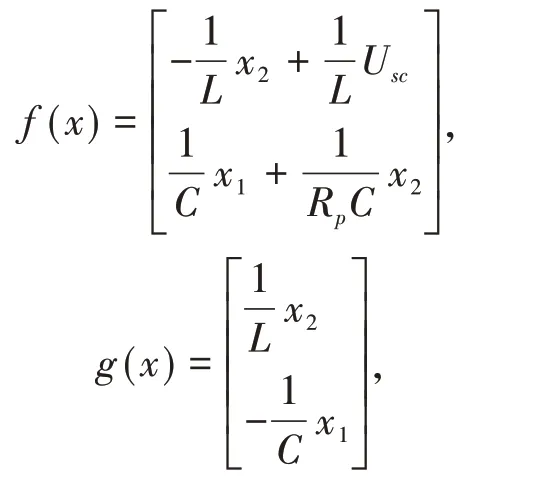
f(⋅)为未知非线性函数；u和y为控制输入和对象输出；d(t)为干扰，|d(t)|≤D.

通过推导和分析可以到的本文设计的控制系统可以满足Lyapunov理论的稳定性要求sṡ<0（限于篇幅推导过程略去）.针对车载超级电容控制系统中f(⋅)是未知的，则可以采用RBF神经网络逼近f(⋅).

（2）车载超级电容控制系统的精确反馈线性化.

由于车载超级电容控制系统满足非线性系统精确线性化条件，因此对其进行线性化.假设反馈线性化过程中以v1，v2为状态变量，进而可以构建系统模型的输出函数m(x).

通过推导分析可以得到反馈线性化的状态变量系统方程为：

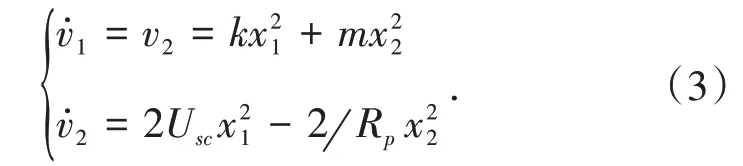
2 基于RBF神经网络自适应鲁棒滑模控制器的设计

根据车载储能系统具有非线性特性，且易受扰动影响的特点，采用系统的参数摄入和扰动无关的滑模变结构控制算法进行控制器设计，通过控制量的切换使系统沿着滑模面滑动.为了克服该方法在实际控制系统中，状态轨迹容易在滑模面两侧产生抖振的现象，加入了神经网络，以逼近滑模面和控制量之间的非线性关系，以保证系统具有很好的鲁棒性和抗干扰性.

本文采用一种具有单隐层的3层前馈网络RBF神经网络，其可以逼近任意非线性和线性的函数.其结构图如图2所示.本研究采用RBF神经网络滑模逼近滑模面和控制量之间的非线性映射关系，以切换函数s=e+cė和导数ṡ作为RBF网络的输入，其中e=θd-θ，将车载超级电容的电压或电流与其参考电压或电流的差值作为控制目标，滑模控制器u作为其输出，其基于RBF的自适应滑模控制系统结构如图3所示.

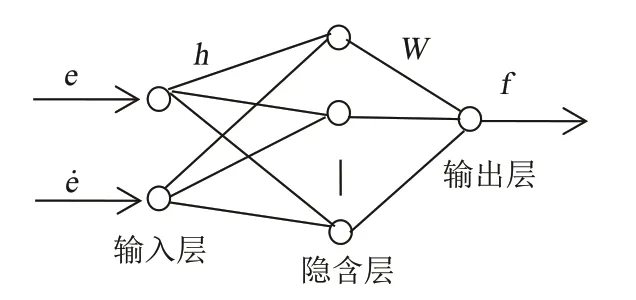
图2 一种3层前馈网络RBF神经网网络结构图Fig.2 Structure of 3-layer feedforward network RBFNN

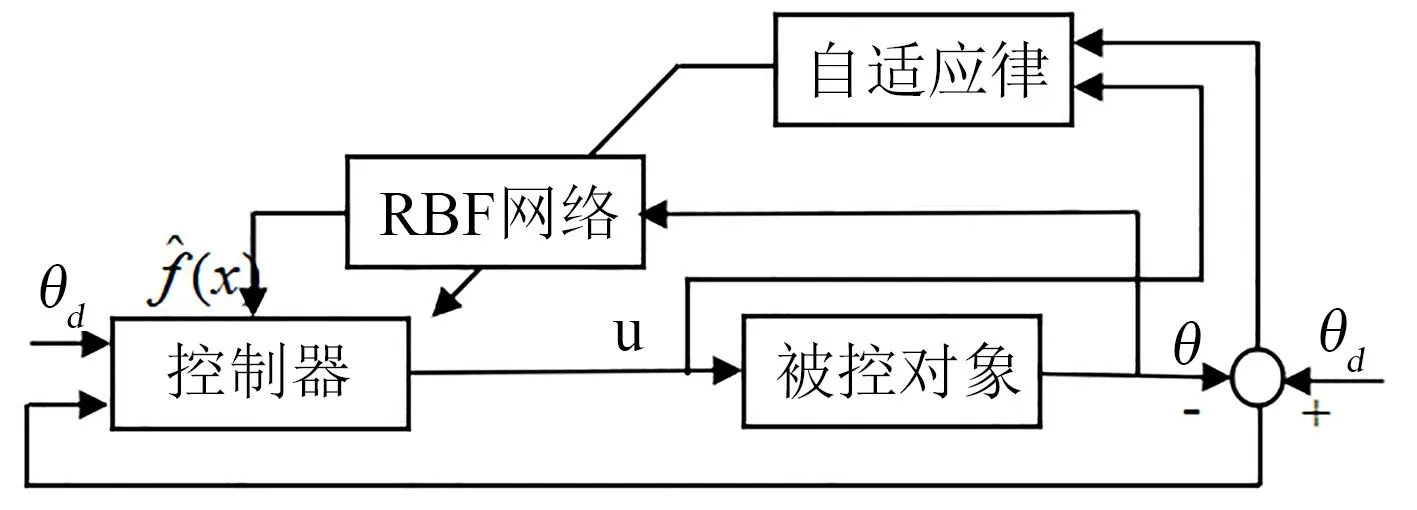
图3 基于RBF的自适应滑模控制系统结构图Fig.3 Structure of adaptive sliding mode control system based on RBF

神经网络的输入为系统期望值和实际值的误差及其导数，考虑设计RBF神经网络激励函数和系统输出分别为：

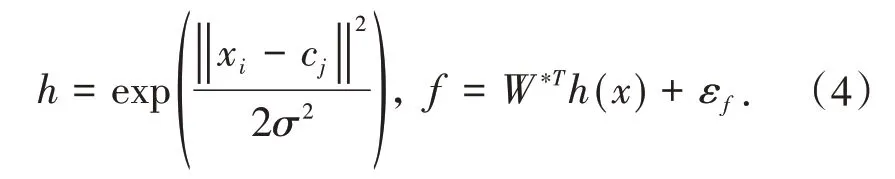
其中，x为网络输入；i表示网络输入层第i个的输入，j为网络隐含层第j个网络输入；h=[hj]T为高斯基函数的输出；W*为理想网络权值；εf为网络逼近误差，εf≤εN；f为网络输出.

根据系统的非线性特点和线性化分析，本研究设计的的RBF神经网络滑模控制器采用的指数趋近率为［12-16］：ṡ=-ks-εsgn(s)，其中k和ε为大于0的常数，根据干扰对自适应不连续控制率的影响，可以设计控制律为：

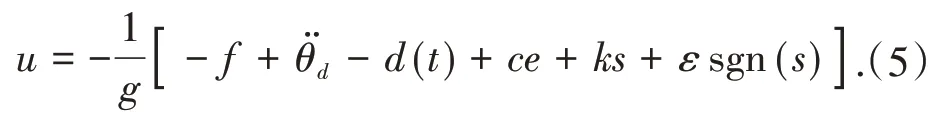
设计Lyapunov函数为：

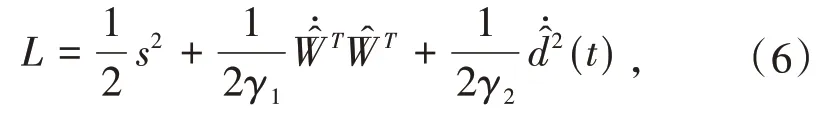
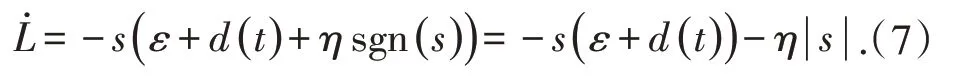
由于RBF网络逼近误差ε为很小，取η≥εN+D，则L̇≤0.当L̇=0时，s≡0，根据Lasalle不变集原理，闭环系统渐进稳定，t→∞时，s→0.可见控制律中的鲁棒项ηsgn(s)的作用是克服干扰和神经网络逼近误差，以保证系统稳定.

3 仿真验证

本研究通过列车在某轨道线路上1.95 km的一个运行区间内进行了仿真实验，其中的各项参数参照文献［12，17-18］：选用30 F的超级电容，工作额定电压为500 V，工作电流为-400A~+400 A.双向DC/DC变换器参数为：储能电感7.5 mH，滤波电容30000 μF.IGBT开关频率10 kHz；直流牵引网标准供电电压1500 V.

利用Simulink建立了车载超级电容单列车的仿真模型（如图4所示），可以根据此很好地对所设计的储能系统进行仿真.

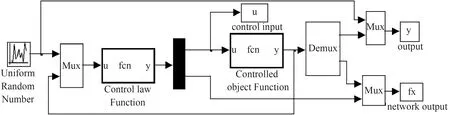
图4 基于RBF网络的车载超级电容滑模控制系统的Simulink结构图Fig.4 Simulink structure of vehicle super capacitor sliding mode control system based on RBF network

从仿真图5中可以看出：使用所设计的储能系统优化后，列车在加速和减速阶段的牵引网电压变化明显比较平缓，最大可以降低27.7%，所提出的算法很好地实现了系统电压的稳定，进而使得这部分能量得到吸收和利用.

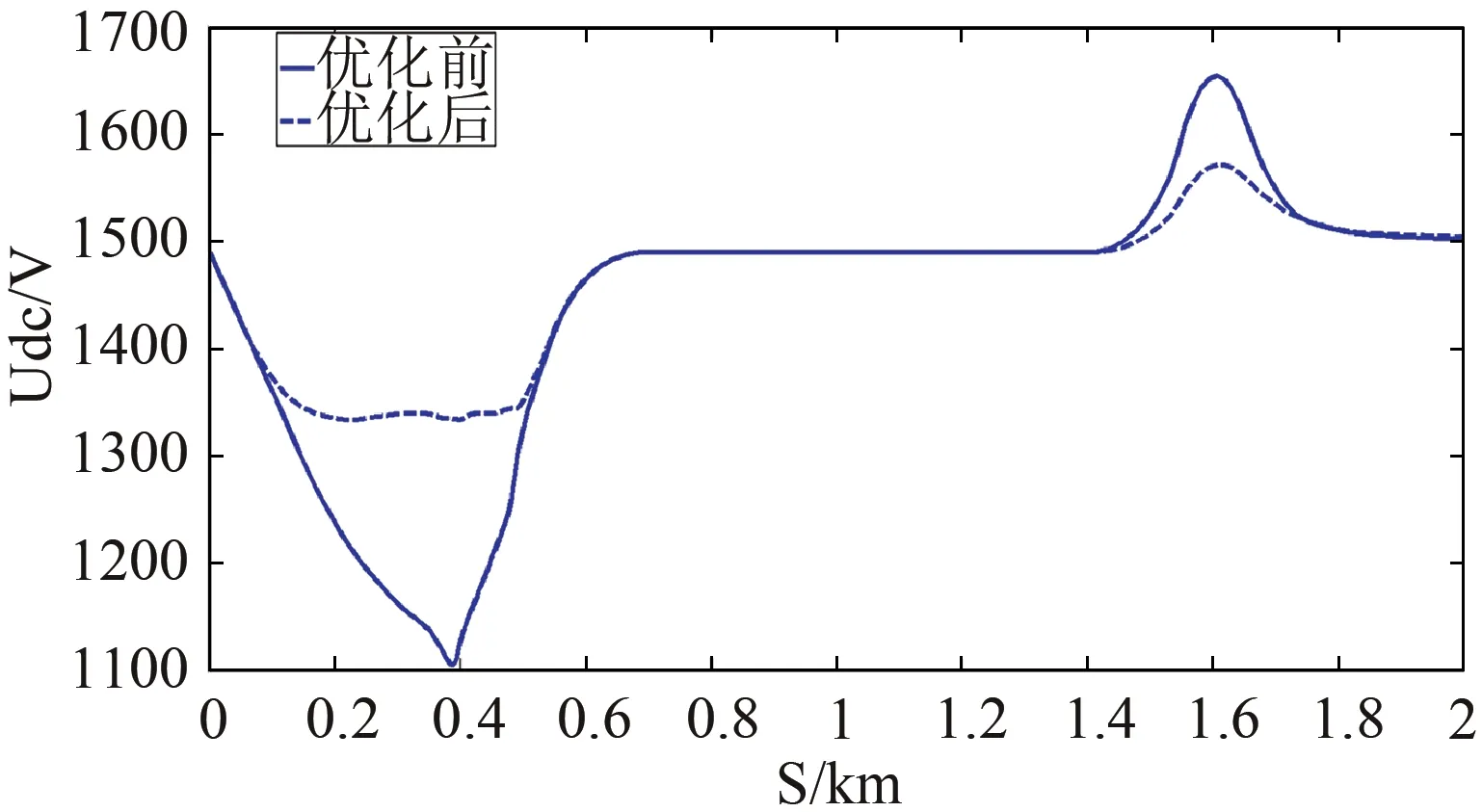
图5 优化前后牵引网电压变化曲线图Fig.5 Traction network voltage variation curve after optimization

从图6中可以看到，所设计的神经网络自适应滑模控制可以很好的跟踪和实现列车速度运行曲线，使得控制系统的响应速度和稳态误差明显改善，外界抗干扰能力增强，具有更好的鲁棒性，使驾驶更加舒适、安全、平稳.

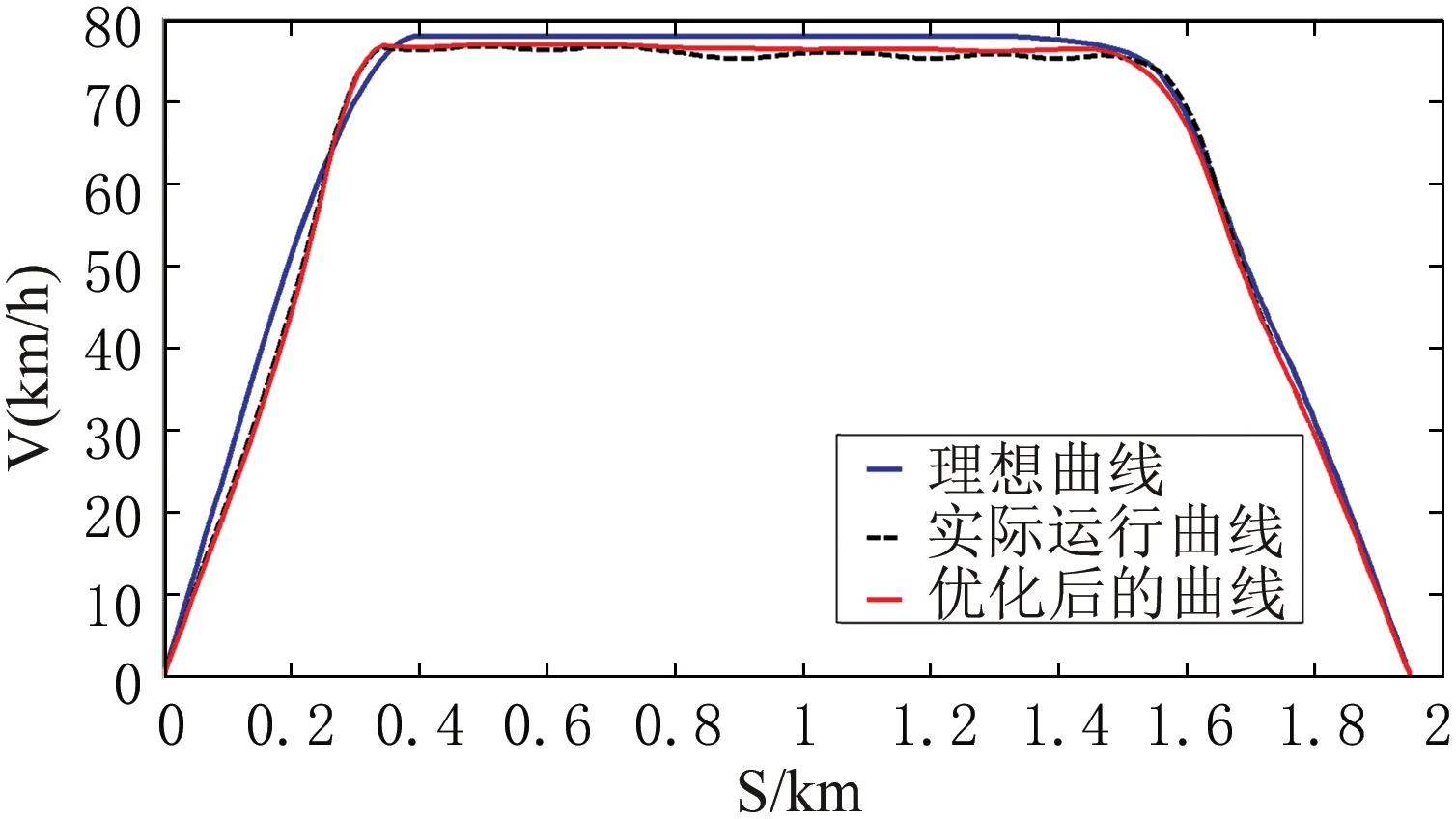
6优化前后的列车运行曲线变化Fig.6 Train operation curves after optimization

从图7中可以看出，使用所设计的神经网络自适应滑模控制方法进行优化，可以使牵引网的能耗降低84.06%，实现了线路损耗大大减小，充分利用了能量.图8中，所提出的算法和RBF网络、RBF自适应网络进行比较，可以看出该算法有效利用了系统整体能量，从优化前的1.595 kW·h降低到0.38 kW·h左右，系统能量损耗降低了37.4%，提升了系统能量利用效率，达到了节约能源目的.

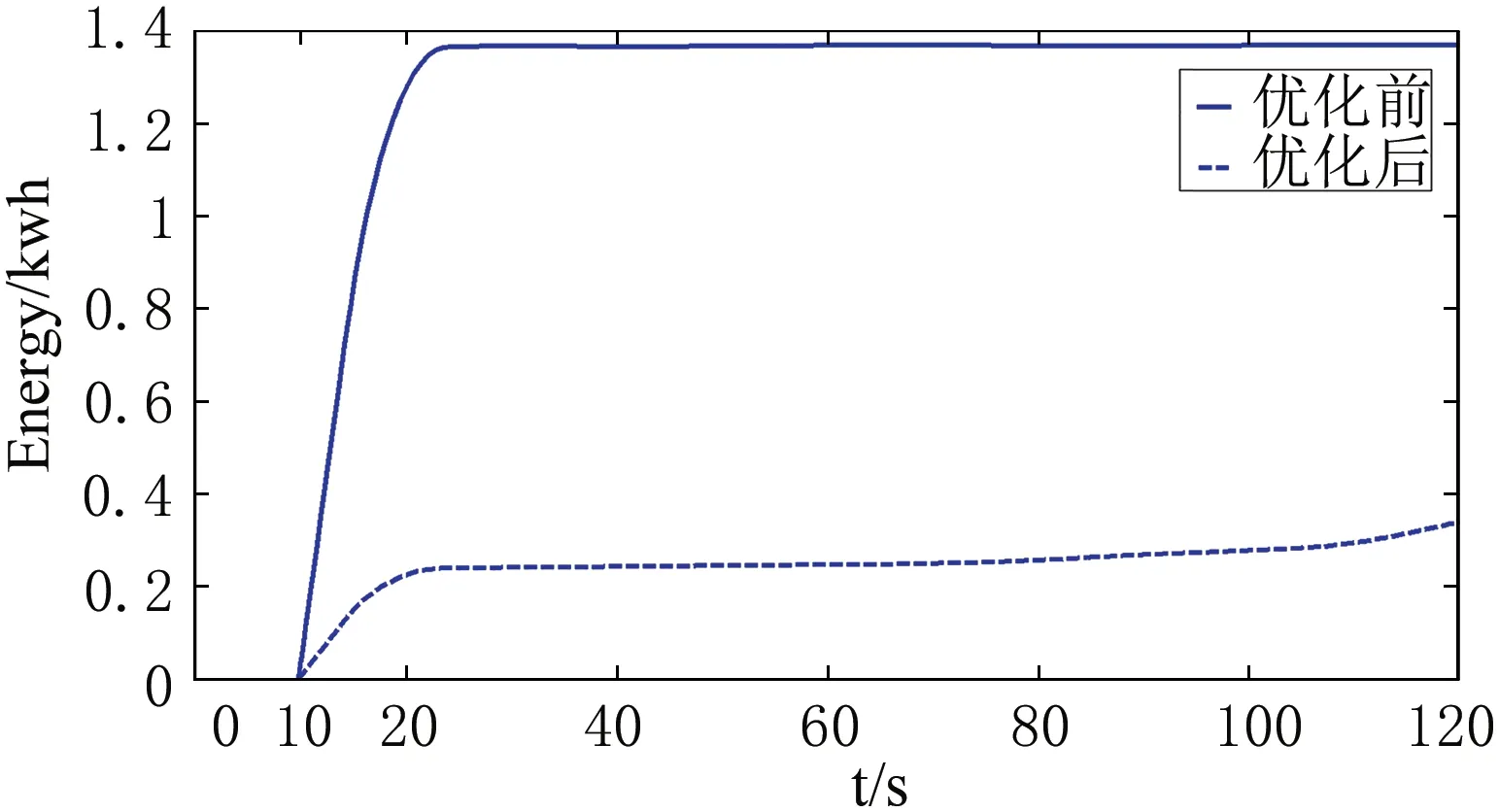
图7 牵引网线路损耗变化Fig.7 Line loss change of traction network

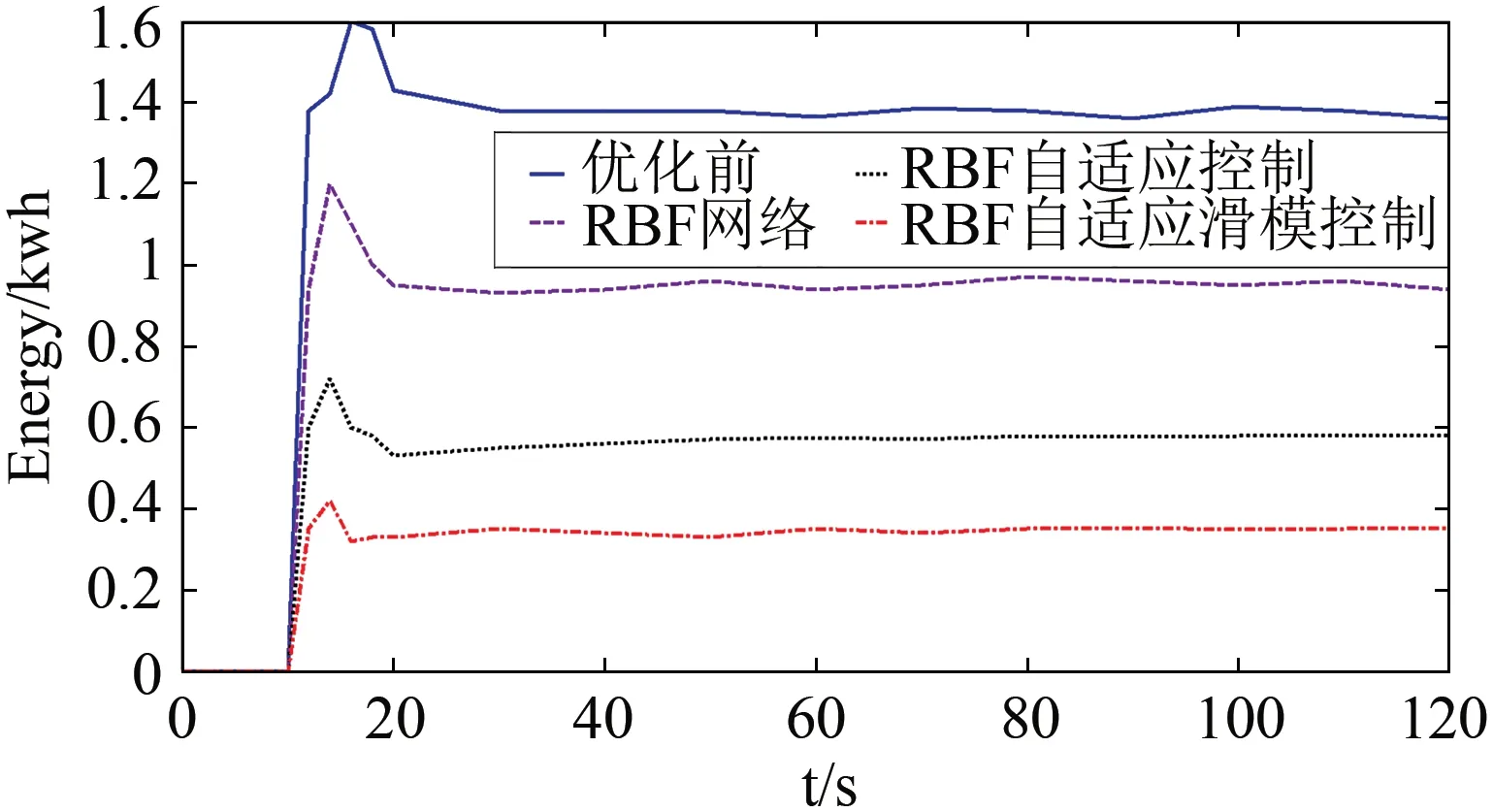
图8 不同控制方法能耗利用比较Fig.8 Energy consumption utilization comparison curves

从上述分析可知，车载超级电容储能系统可有效利用列车再生制动能量，且能抑制网压波动，减小牵引网线路损耗，证实了该算法的稳定性和有效性.

4 结论

（1）超级电容以其功率密度高、循环使用寿命长等特点在解决城轨列车再生失效、改善列车高速制动力不足、可以实现无馈电线运行等方面有着独特的优势和发展前景，使驾驶性能实现最优.

（2）本文提出的基于神经网络超级电容自适应滑模控制系统，通过仿真研究，验证了该系统具有抑制网压波动、减小牵引网线路损耗和提高再生制动能量利用率等功能.