基于MpCCI的载荷转换方法研究

王昌林，李 磊，王全红

(中国飞机强度研究所，陕西 西安 710065)

1 引 言

机翼是与飞机气动和结构这两部分关系最密切、最复杂的部分。在对机翼结构进行静力、疲劳试验及结构有限元分析的过程中，需要将机翼表面产生的气动载荷转换到结构上。气动载荷在设计阶段通常采用CFD的方法获得，在计算之前必须对计算区域进行离散化处理，将空间上的计算区域划分为多个子区域，并在每个子区域中确定节点，生成网格，即气动网格点压力离散场的形式出现。此方法需要划分规模巨大的网格来进行计算，所产生的气动载荷数据量也很巨大，而进行结构试验或有限元分析时所使用的加载节点或计算网格规模较小，此二者之间的数量相差几个甚至几十个量级，此时需要将气动载荷从气动网格节点转换到试验加载节点或有限元分析所用的网格节点上。此外，气动力加载会引起结构变形，而结构变形会引起气动外形的变化，造成气动力分布的改变，需要在变形后的两个网格之间产生位移和力的互相传递。因此，加载到结构上的载荷能否精确地反映气动特性非常重要。

常用的二者之间载荷转换与传递的方法有以下几种：三点排[1]、四点排[2]、多点排[1]。这三种方法在原理上只支持气动载荷向有限元节点载荷的转换与传递，并不支持载荷引起的结构变形信息向气动外形的反馈传递。

本文使用MpCCI作为载荷转换方法，分别与以上几种方法进行过程与结果的对比，通过算例说明这种方法在实际应用中的意义，以期为进行机翼结构静力、疲劳试验及有限元分析等过程中载荷转换方法的选择提供参考。

2 常用载荷转换与分配方法

2.1 三点排方案

三点排(如图1所示)表述了如何将气动节点A上的载荷PA按照静力等效的原则分配转换到邻近的3个结构节点上[3]。

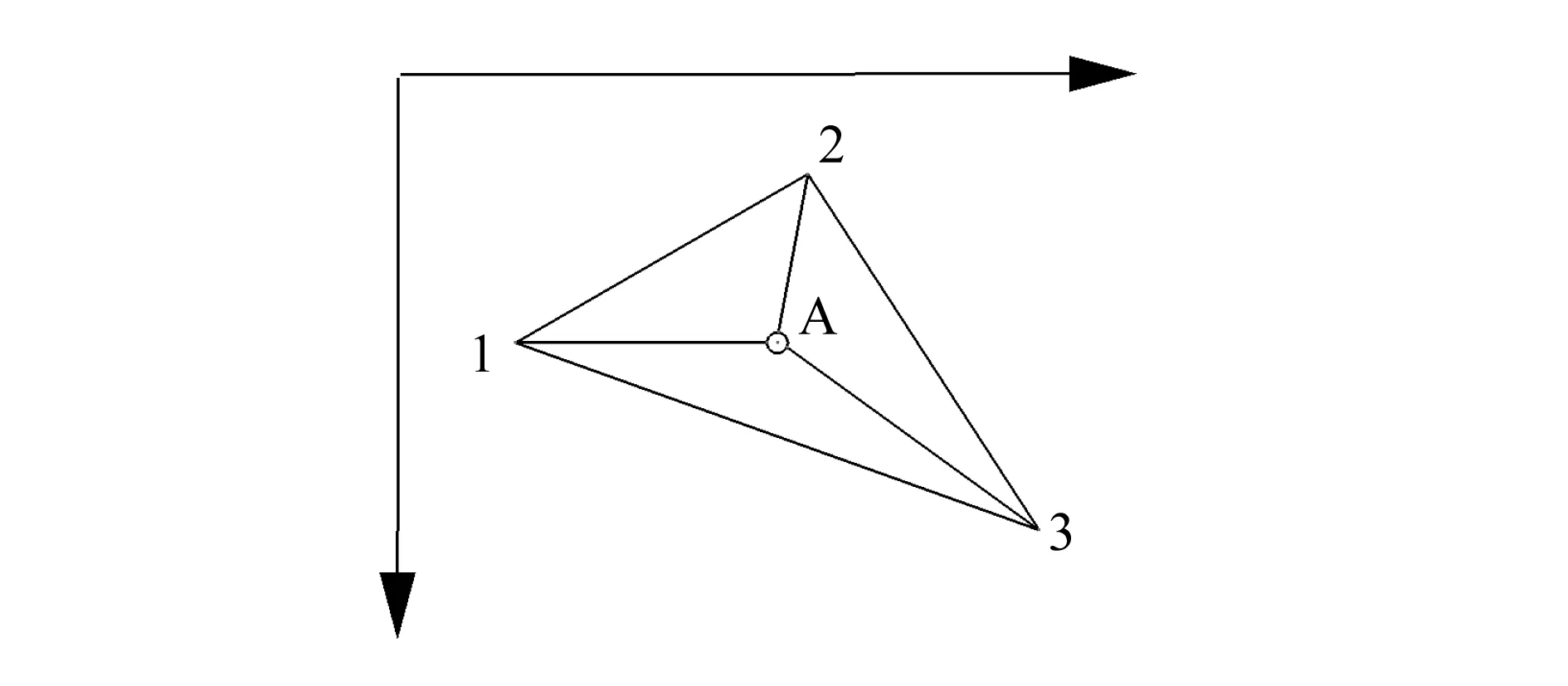
图1 三点排示意图

假设选定点1、2、3作为结构节点，那么气动点A分配到这3个有限元节点上的载荷计算公式如下：

(1)

式中，PA为气动节点A上的载荷；A、A1、A2、A3分别为△123、△A23、△A13、△A12的面积。

对所有的气动节点载荷都依据式(1)计算得到对应的结构节点载荷[4]，然后把同一结构节点上分配到的载荷叠加起来，即为这一结构节点上的总载荷。

2.2 四点排方案

四点排示意图如图2所示，横纵向实线分别表示长桁与肋的布置线，四点排就是将气动载荷节点C上的气动力转换到结构的结构布线的节点上。

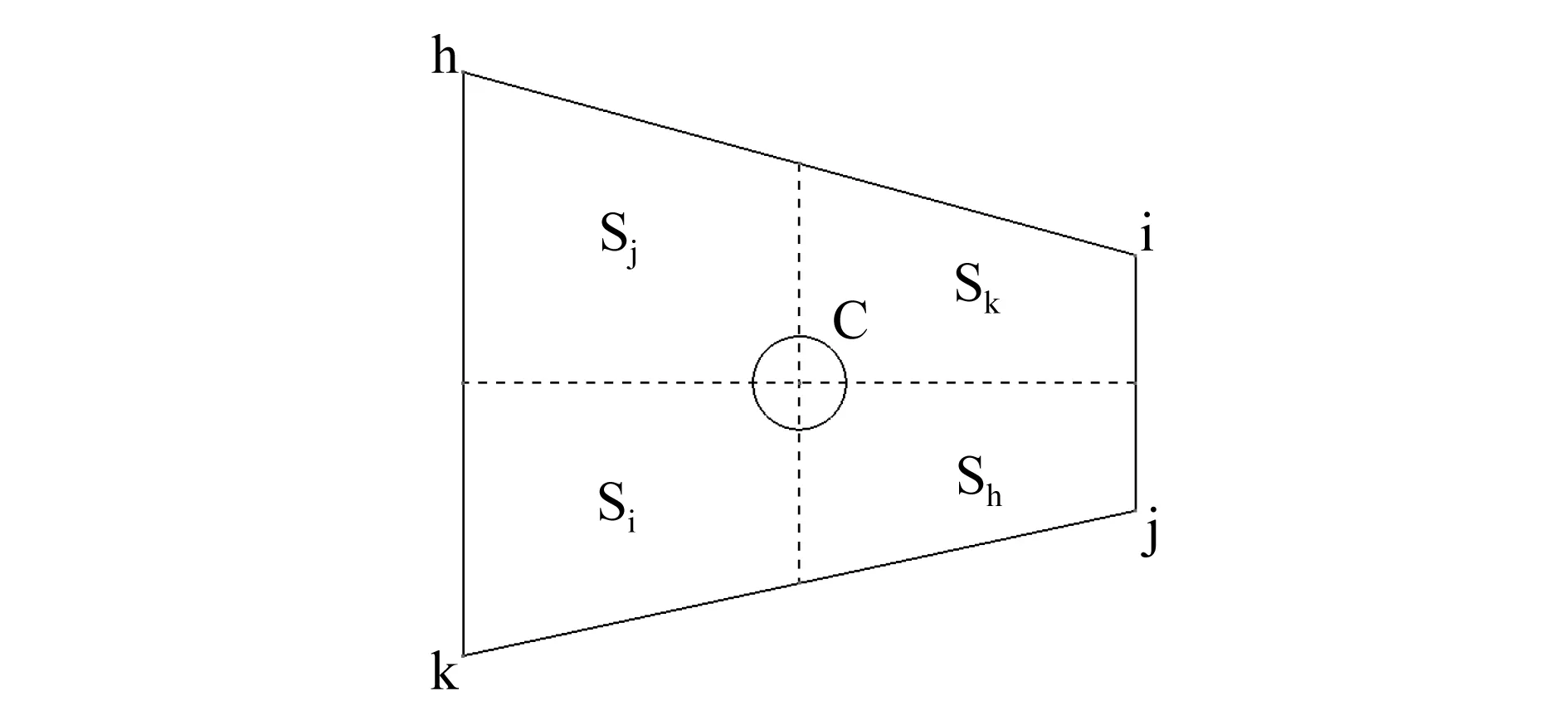
图2 四点排示意图

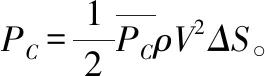
(2)

2.3 多点排方案

多点排方案(如图3所示)的基本思路为：在分配过程中，距离气动节点近的结构节点分配权重大一些，反之小一些。假设有一根无形的悬臂梁处于结构节点和气动节点之间，EL为假想悬臂梁的抗弯刚度[5]。这根梁在气动节点的一端为固支，自由端上的结构节点分配到载荷Pj时，其变形能力为：

(3)

图3 多点排示意图

那么，对于由所有结构节点与某气动节点组成的所有假想悬臂梁系统而言，其变形能力为：

(4)

根据最小势能原理计算分配到结构节点上的载荷，在满足连续条件和边界条件的位移中，满足平衡条件的位移其总势能最小，那么欲使其系统变形能量最小，同时还应满足静力等效条件：

(5)

(6)

(7)

式中，n为结构节点数。

采用拉格朗日(Lagrange)乘子法建立拉格朗日函数：

(8)

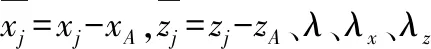
为了使F(λλxλz)能够取最小值，令：

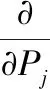
(9)

得：

(10)

整理公式得：

由上式解出λ、λx、λz后，代入式(10)中即可得到结构节点所分配到的载荷Pj。对整个气动节点网群上的每一个气动载荷，按上述方法分配，就得到了所期望的载荷转换结果。

几种常用载荷转换方法的基本思路如上文所述，都遵循了静力等效和能量原理。值得注意的是，在实际应用过程中，往往需要解决的是成千上万气动节点向成百上千结构节点转换载荷的问题，通过手工计算解决上述问题是不切实际的，此时就需要借助计算机以及有关软件的帮助。此外，气动载荷的取得途径是多样的，常用的CFD软件也种类繁多。上述3种载荷转换的方法，针对不同来源的气动载荷和不同形式的结构模型，处理起来也不够友好、通用性也不强，在处理过程中需要编写不同的接口程序来满足转换过程中上、下游数据流通的需要。

2.4 MpCCI方法

采用MpCCI进行载荷转换的基本过程是：直接调用CFD软件对结构的外流场进行计算或调用已有的气动载荷，在耦合界面处提取气动载荷，进行载荷转换输出结果或者直接将结果提交给用户程序。由于气动节点组成的网格和结构节点组成的网格的计算要求不同，在力的传递界面上网格不匹配，节点是不重合的，从而不能直接进行数据交换，需要在传递界面上采用映射的方法。这里用Nf和Ns分别表示对应气动网格和结构网格上的节点，如果Nf和Ns不重合，可使用一定的算子映射来进行计算，表示为：

Msf:{fi|i∈Nf}→{fi|i∈Ns}

Mfs:{fi|i∈Ns}→{fi|i∈Nf}

上式中，fi和si分别为传递边界上气动、结构节点的矢量。由于气动域和结构域的网格不同，即Msf≠Mfs-1。

在边界上气动节点的位移如下：

uf=Msfus

力的平衡条件是将气动节点力先映射到结构节点，然后通过积分得到结构节点力，在此过程中采用固体边界的插值函数。

式中，HST是记录结构单元沿着边界的插值函数，这样就可以计算出结构模型的节点力，在有限元模型计算的过程中作为边界条件使用。

3 算例对比

3.1 二维梯形机翼沿展向椭圆分布弦向三角形分布

气动载荷沿梯形机翼的展向呈椭圆分布、沿弦向呈三角形分布。弦向分布方程：在0到0.4以内为0.8x+0.2，在0.4到2为-0.56x+1.22。其中，气动节点的数目为189，结构节点的数目为78，气动分布图和网格节点示意图见图4、图5。

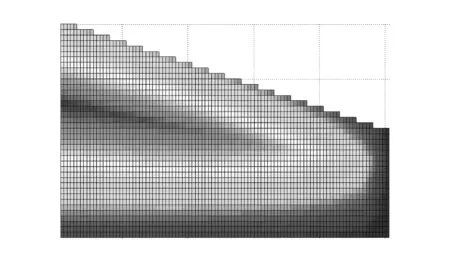
图4 气动分布图

图5 网格节点示意图

经过三点排、四点排、多点排、MpCCI等方式进行载荷转换后，所得结果如图6、图7所示。

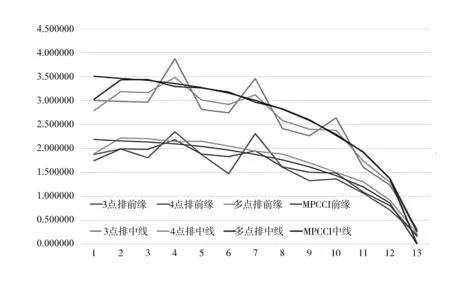
图6 展向节点载荷分配示意图

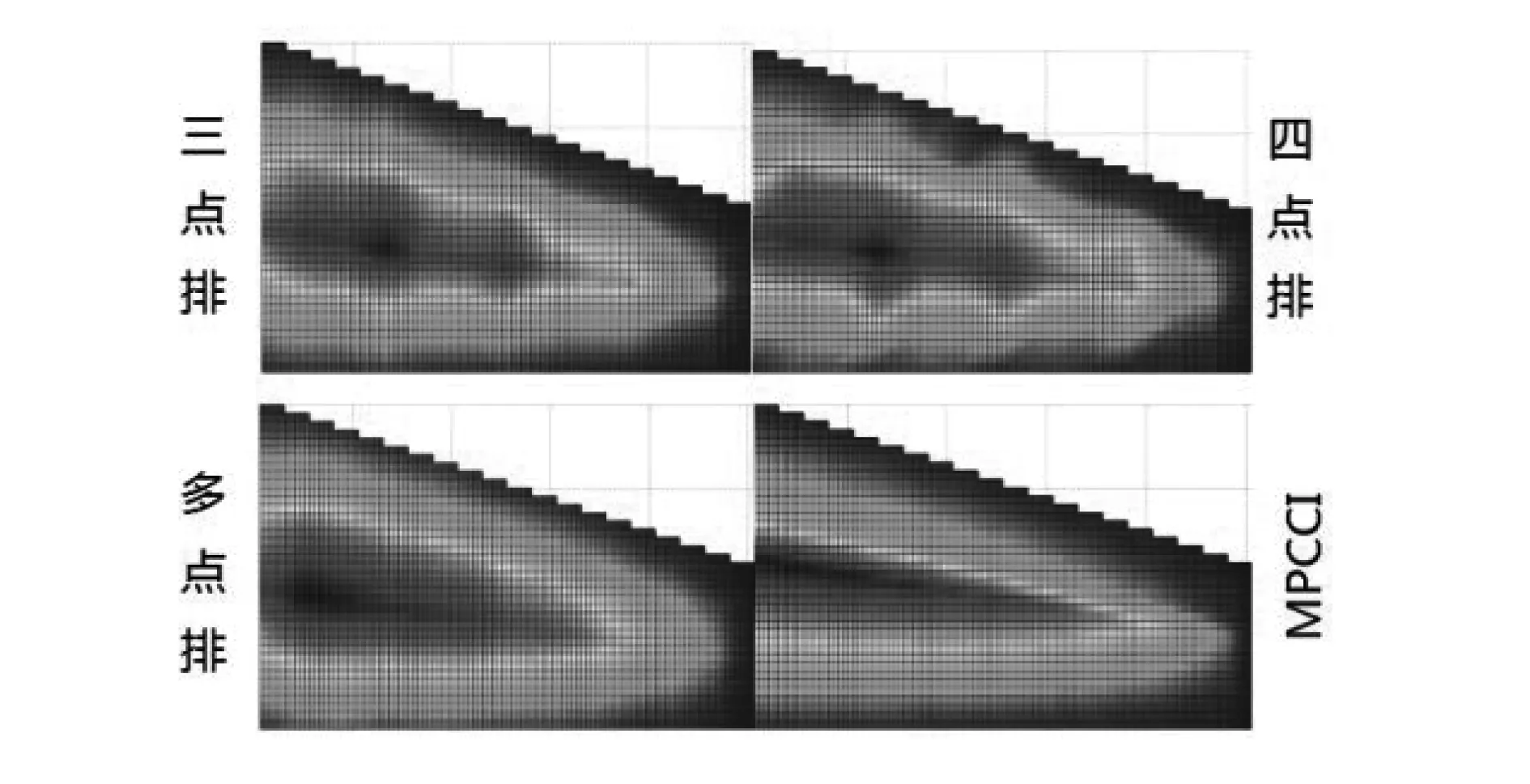
图7 结构力云图

从图中可以看出，三点排和四点排方案所取得的载荷有着很大幅度的跳跃，且最大分配载荷明显比多点排和MpCCI所取得的载荷大。与三点排和四点排相比，多点排方案有了很大的改善，但与MpCCI取得的结果相比还是有差距的。MpCCI取得的结果呈椭圆分布，基本没有出现跳跃，分布的规律更接近于气动载荷，曲线也最为光滑。表1给出了各方法所取载荷与原气动载荷的相关系数。

表1 各方法所取载荷与原载荷相关系数

3.2 二维平直机翼沿展向椭圆分布弦向三角形分布

平直机翼的气动分布与上文的梯形机翼的气动分布一致，气动节点数为189，结构有限元节点数为78，气动分布图和网格节点示意图见图8、图9，各载荷转换方式的展向节点载荷分配及结构力云图如图10、图11所示。

图8 气动分布图

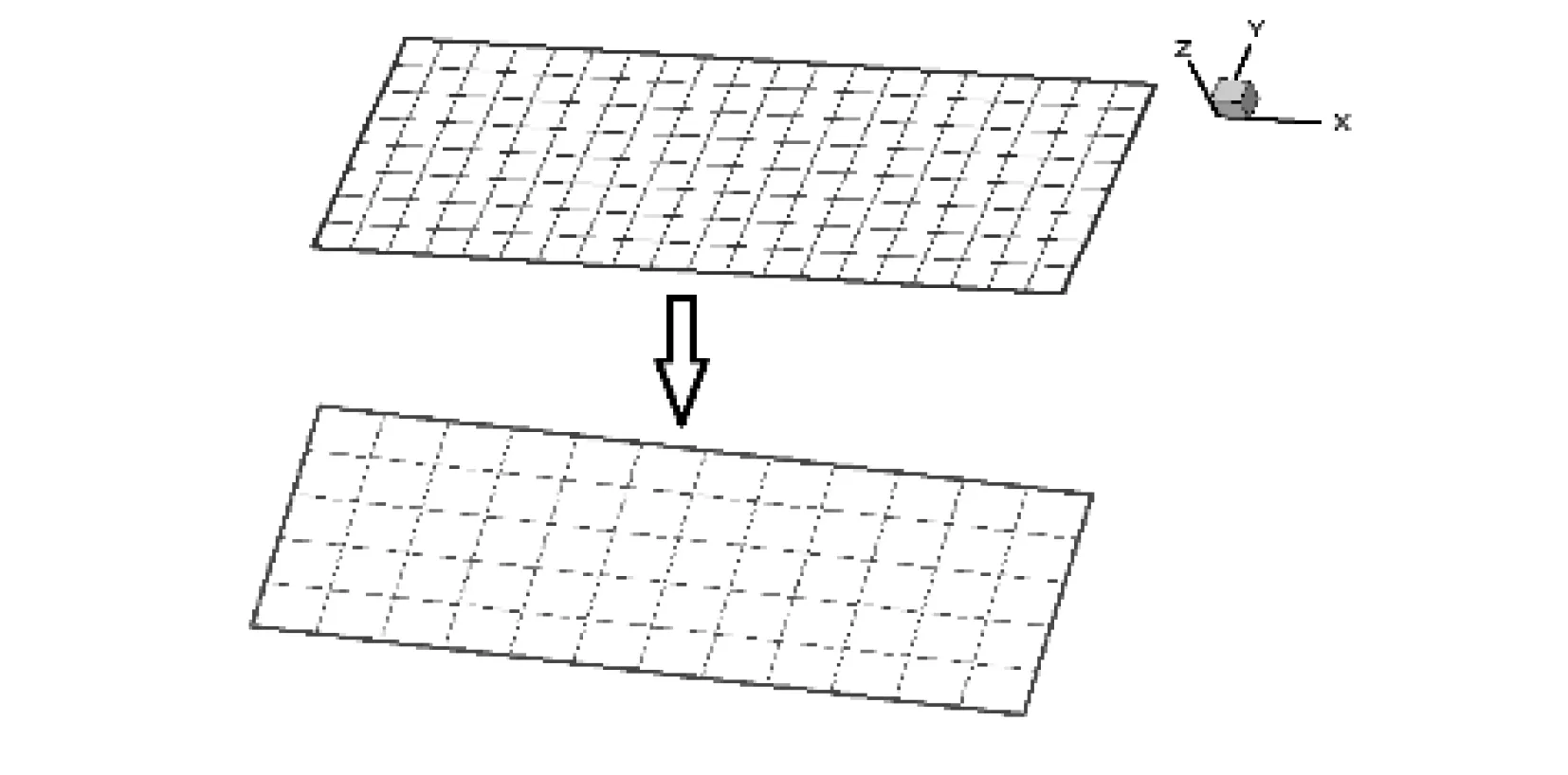
图9 网格节点示意图

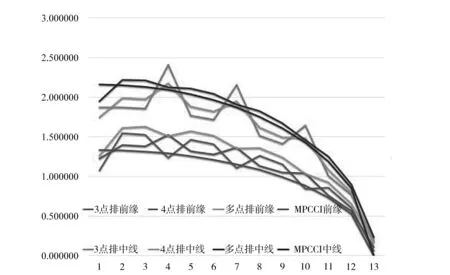
图10 展向节点载荷分配示意图

图11 结构力云图

从图中可以看出：无论是中线还是前缘，这几种载荷转换方式下，MpCCI取得的结果最接近真实气动载荷，跳跃小，过渡最为光滑。表2给出了各方法所取载荷与原气动载荷的相关系数。

表2 各方法所取载荷与原载荷相关系数

3.3 小 结

从以上两个算例可以看出，MpCCI在气动载荷转换为结构有限元载荷方面，比其他转换方法精度更高。

4 三维机翼载荷转换实例

M6机翼为跨音速试验验证机翼，展长1.1963m，前缘后掠角30°，后缘后掠角15.8°，机翼面积0.7537451m2，蒙皮厚度0.0045m，梁腹板厚度0.011m，翼肋厚度0.006m，材料为铝合金，弹性模量E=70GPa，泊松比μ=0.33。

外流场网格划分使用的是ICEM软件，总共划分了73万个网格。计算气动力的软件为FLUENT，模型单位尺寸为毫米；三维基于密度隐式求解器，K-ωSST湍流模型，湍流强度1.86%，采用二阶迎风格式，流场进口使用压力远场边界条件。气动网格如图12所示。

图12 气动网格

结构模型网格划分使用的是SimXpert，总共划分网格数量为1075，其中所有节点均为梁肋布置线的交点，结构有限元网格如图13所示。本文对机翼结构模型作了适当简化：

(1)只考虑了组成承力翼盒的主要部件：蒙皮、梁腹板、翼肋，长桁和梁缘条厚度“打扁”后计入蒙皮的厚度，以减少有限元模型的复杂程度和计算量，文献[6]和文献[7]均采用这种简化方法；

(2)在实际的机翼结构中，上下蒙皮厚度、前后梁腹板厚度是沿展向变化的，本文认为蒙皮厚度、梁腹板厚度沿展向是不变的，同样是为了减少模型的复杂程度；

(3)在实际情况中，机翼和机身的连接情况是复杂的，本文假设机翼根部为固支。

图14为在MpCCI中载荷转换过程。

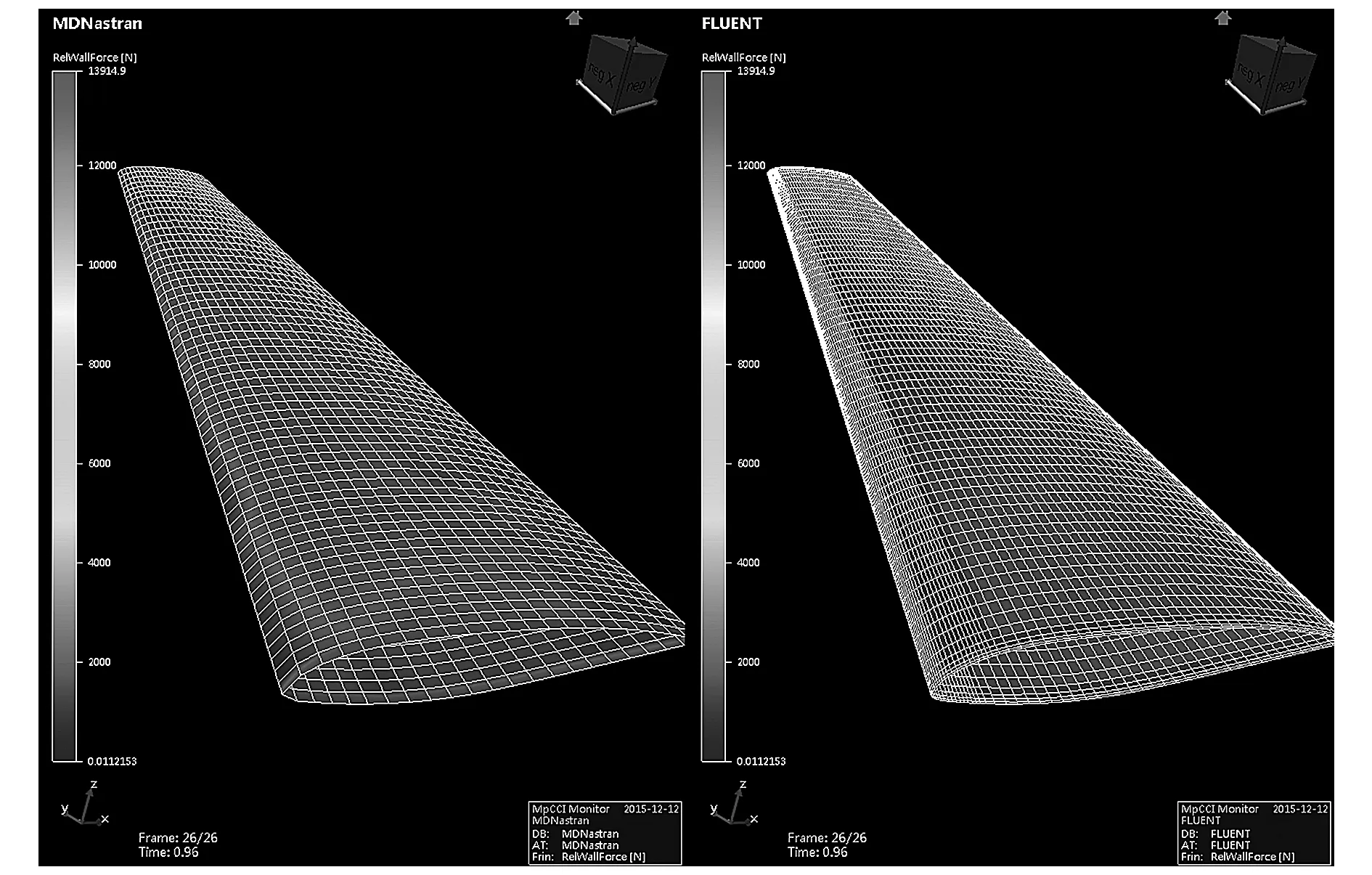
图14 转换过程

载荷转换结果分析：由于是将载荷转换后提交Nastran进行计算，所以根据Nastran不同的设置可以得到不同的输出结果。图15是输出的机翼上下表面应力云图，可以看出，应力云图的分布与气动力的分布一致。此外，计算所得翼尖的位移为0.0065m，这基本与试验值相符合。

在以往的研究中，通过Fluent、Star-CD、CFX等CFD软件实现了与结构有限元软件之间的单向流固耦合，这样没有真正地实现数据在迭代求解过程中的动态传输，降低了求解精度，与实际情况有着较大的差异。借助MpCCI双向流固耦合接口，将有限元软件与CFD程序软件进行连接，实现了多相耦合，多维度耦合分析，以及动态双向流固耦合分析。同时，MpCCI能够将绝大多数的CFD软件和有限元软件以及热力学软件耦合起来，还可以使用简单的代码将Matlab等工具结合起来。

5 结 论

本文使用MpCCI作为气动节点载荷向结构有限元节点

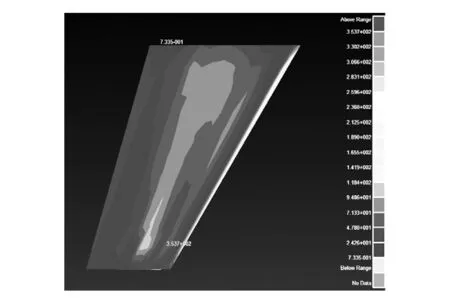
图15 机翼上下表面应力云图

载荷转换的平台，通过算例，对比分析了其与传统转换方法之间的差异，突显出了这种方法在使用上的优越性。研究结果表明，MpCCI在转换精度上优于传统方法。

同时，本文通过MpCCI对FLUENT和NASTRAN的调用，模拟并取得机翼结构在气动加载条件下的响应，显示了MpCCI强大的通用性，除了用于载荷转换外，在多物理场耦合方面也有强大的作用。此方法有一定的计算效率、精度及工程应用价值。