用转置矩阵求解静不定桁架的内力

李苗苗，吴 晓

(1.常德职业技术学院土建系，湖南 常德 415000；2.湖南文理学院机械工程学院，湖南 常德 415000)

1 引 言

由于平面静不定桁架、空间静不定桁架在工程实际中得到了广泛应用，因此寻求简洁、清晰的方法来求解静不定杆系内力，对工程力学教学及工程设计是有理论指导意义的。文献[1]采用拉格朗日法研究了静不定梁、圆弧、刚架、平面桁架的内力求解；文献[2]在文献[1]的基础上，采用拉格朗日函数法研究了杆系装配应力的求解；文献[3]采用数学微分法研究了静不定空间桁架内力的求解。以上方法研究平面静不定桁架、空间静不定桁架内力求解时，仍存在计算繁琐复杂的不足。本文通过研究发现，采用转置矩阵研究静不定杆系的内力求解，与其它方法相比具有简洁、清晰的优点，更易于学生和工程设计人员掌握和应用。

2 力与位移转换矩阵证明

以图1所示受力弹性体为例，设坐标原点O的力系为(XO，YO)，将此力系平移到A点时，可知A点的力系为(XO，YO，M)，且附加力偶M为：

M=XOyA-YOxA

(1)

式中，xA、yA分别为A点横坐标、纵坐标。

图1 受力弹性体示意图

因此，可把力系(XO,YO)与力系(XO,YO,M)之间关系用矩阵表示为：

(2)

令u、v分别为与XO、YO对应的广义位移，设弹性体有一位移可用A点的平移uA、vA和绕A点的转角θA表示，所以，O点位移(uO,vO)与A点位移(uA,vA)之间关系可用矩阵表示：

(3)

比较式(2)与式(3)可知，右侧的两个矩阵是互为转置矩阵。

力系(XO，YO)在位移(uO，vO)做的功及力系(XO，YO，M)在位移(uA，vA，θA)做的功分别为：

WO=XOuO+YOvO

WA=XOuA+YOvA+MθA

(4)

把式(3)代入式(4)中，可得WO=WA，所以对于弹性体来说，静力等效力系也就是功等效力系。

对式(2)、式(3)进一步分析，可以看出，式(2)表示两组功等效力系的相互关系，一般可写成：

{P}Ⅰ=[A]{P}Ⅱ

(5)

式中，{P}Ⅰ和{P}Ⅱ是两个功等效力系，[A]称为力转换矩阵。

式(3)表示与两个力系对应的两组广义位移之间的关系，以{δ}Ⅰ、{δ}Ⅱ分别表示这两组广义位移，则式(3)可表示为：

{δ}Ⅱ=[B]{δ}Ⅰ

(6)

式中，[B]称为位移转换矩阵。

由于已设力系{P}Ⅰ和{P}Ⅱ为等效力系，则有：

(7)

把式(5)代入式(7)中，可得：

(8)

由于式(8)对于任何力系都成立，所以可得：

{δ}Ⅱ=[A]T{δ}Ⅰ

(9)

对比式(6)、式(9)可以知道，右侧的两个矩阵是互为转置矩阵，即：

[B]=[A]T

(10)

因此，已知{P}Ⅰ=[A]{P}Ⅱ，必有{δ}Ⅱ=[A]T{δ}Ⅰ成立。

3 问题的求解步骤

为了说明转置矩阵在求解静不定杆系内力中的应用，下面着重阐述协调条件的建立。

3.1 力系方面

假设静不定杆系是n次静不定的，因此共有n个多余未知反力Xi(i=1,2,…,n)，可写成{X}，把外载荷{F}和多余未知反力{X}作为力系[X⋮F]T。多余未知反力一方面作为加于静定基上的外力，一方面多余未知反力实际上是内力，可把全部内力含广义应力作为内力系{Q}。由于外力功与应变能相等，所以力系[X⋮F]T与力系{Q}是功等效的。

3.2 位移方面

3.3 平衡方程

根据平衡条件，外力系[X⋮F]T与内力系{Q}可以用平衡矩阵联系起来，可得平衡方程：

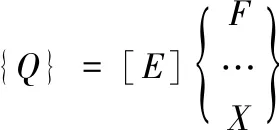
(11)

式中，[E]为平衡矩阵。

由于杆系内力矩阵与位移矩阵是互为转置矩阵，结合以上位移方面对应于{X}的位移为0的说明，可把式(11)化为：

(12)

式中，{δ}为多余未知反力{X}相对应杆件的拉伸或压缩位移的列阵。

在式(12)中，左侧列阵中的分块零列阵{0}共包含n个零元素。因此，可由式(12)列出变形δi(i=1,2,…,n)之间的n个关系式，亦即n个变形协调方程。

4 实例计算

算例1 图2所示杆1和杆2的刚度皆为E1A1，杆3的刚度为E3A3，杆3的长度为l+Δ，其中Δ为加工误差。试求杆3装入AD位置后，三杆的轴力。

图2 平面三角桁架

假设各杆轴力皆为拉力(以下类同)，对A点进行分析可知：

N1=N2,N3=-2N1cosα

(13)

在内力作用下各杆伸长为：

(14)

以N1为未知反力，利用式(11)、式(13)可得：

(15)

再利用式(12)、式(14)、式(15)可得：

(16)

由式(16)可得变形协调条件为：

(17)

由式(17)可以求得：

(18)

此结果与文献[2]给出的结果是一致的。

算例2 图3所示杆系，杆6比名义长度略短，误差为Δ，杆的刚度同为EA，试求将杆6装配到A、C之间后各杆的内力，其中，l1=l2=l3=l4=a。

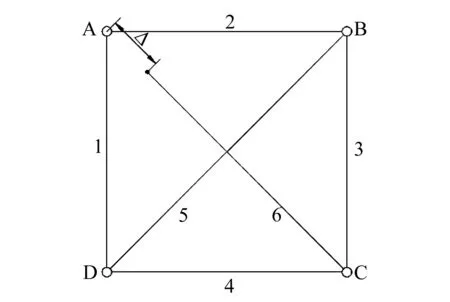
图3 平面杆系

对节点A进行分析可知：

(19)

因结构和载荷均对称可知：

N1=N2=N3=N4,N5=N6

(20)

各杆在内力作用下伸长为：

(21)

以N1为未知反力，利用式(11)可把式(20)写为：

(22)

利用式(12)及有关各式可得：

(23)

由式(23)可得变形协调条件为：

(24)

由式(24)及式(20)可得：

(25)

式(25)与文献[2]给出的结果是一致的。

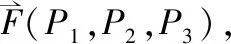
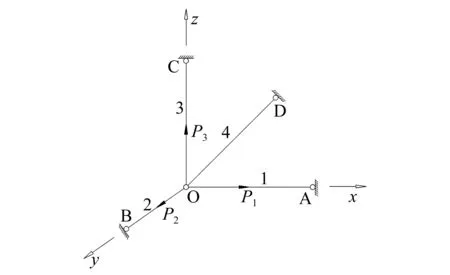
图4 空间4杆桁架

对节点O进行分析，可得x、y、z方向的平衡方程分别为：

(26)

由式(26)可以求得：

(27)

以N4为未知反力，利用式(11)、式(27)可得：

(28)

再由式(12)、式(28)可得：

(29)

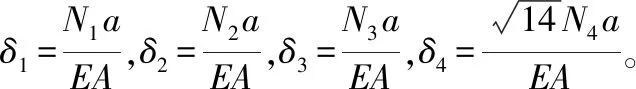
由式(29)可得变形协调条件为：

14N4-N1-2N2-3N3=0

(30)

利用式(30)可求得：

(31)

当P1=2，P2=3，P3=4时，由式(27)、式(31)可得：

N1=-1.6987,N2=-2.3974,N3=-3.0962,N4=-1.1273

(32)

式(32)与文献[3]给出的结果是一致的。

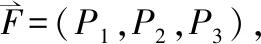
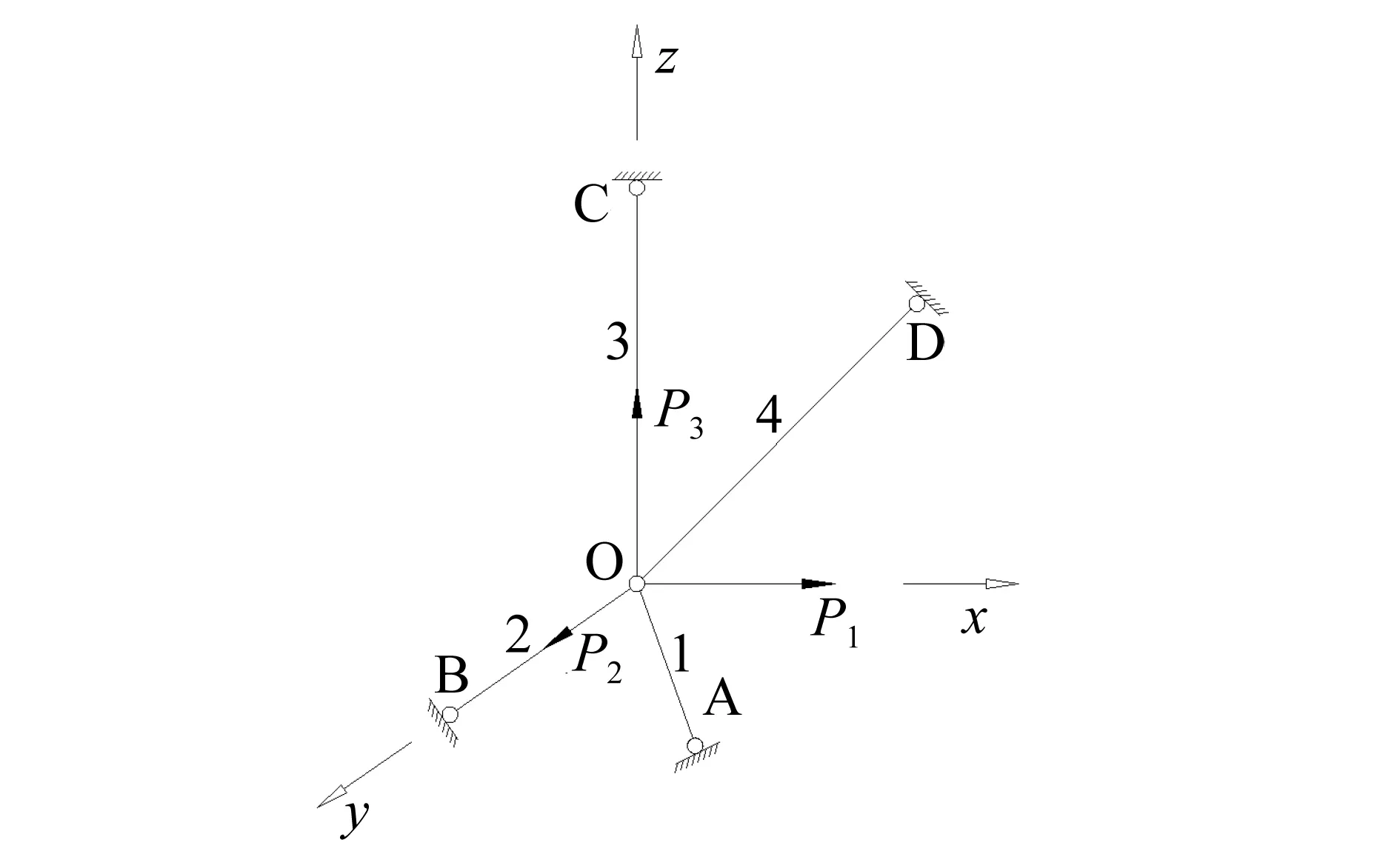
图5 一次静不定空间桁架

对节点O进行分析，可得x、y、z方向的平衡方程分别为：

(33)

由式(33)可以求得：

(34)

以N4为未知反力，利用式(11)、式(34)可得：

(35)

再由式(12)、式(35)可得：

(36)

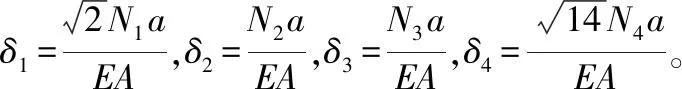
由式(36)可得变形协调条件为：

14N4-2N1-N2-3N3=0

(37)

利用式(34)、式(37)可求得：

(38)

当P1=1，P2=-1，P3=1时，由式(34)、式(38)可得：

N1=-1.331,N2=2.0587，N3=-0.8239，N4=-0.2196

(39)

式(39)与文献[3]给出的结果是一致的。

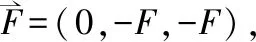
图6 空间杆系

由于A、B、C、D、E五节点共有15个平衡方程，若以N1为未知反力，可求得：

(40)

利用式(11)可把式(40)表示为如下形式：

(41)

式中，

{N}T={N1N2N3N4N5N6N7N8N9N10}，

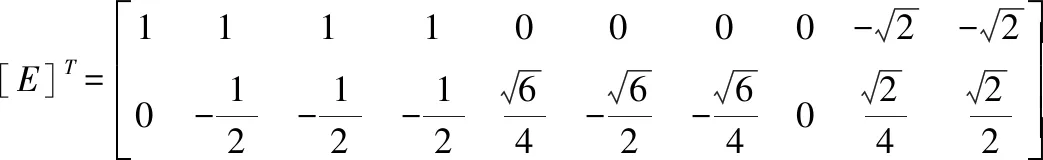
再利用式(12)，可把式(41)化为：

(42)

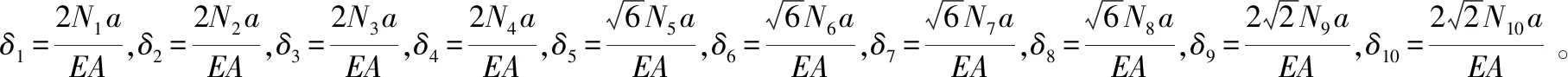
利用式(42)，可得变形协调条件为：

2N1+2N2+2N3+2N4-4N9-4N10=0

(43)

把式(40)代入式(43)中可求得：

(44)

若F=100，可以得到：

N1=37.5，N2=-12.5,N3=-12.5,N4=-12.5,

N5=61.237,N6=-122.474，N7=-61.237,N8=0,

N9=-17.675,N10=17.675

(45)

式(45)与文献[3]中给出的结果是一致的。

由以上算例可知，采用转置矩阵求解静不定杆系内力，利用静力平衡方程可得杆系内力矩阵，而杆系内力矩阵与位移矩阵是互为转置矩阵，得到静不定杆系的变形协调条件后，即可方便求得静不定杆系的内力。

由文献[1]、文献[2]可知，采用拉格朗日函数法研究静不定结构的内力计算具有通用的优点，但是需要引进拉格朗日系数且利用静力平衡方程构造静不定结构能量函数，然后对未知变量求偏导得到变形协调条件后，才能求得静不定结构的内力。

由算例1、算例2可知，采用转置矩阵求解静不定杆系内力，要比采用拉格朗日函数法研究静不定结构内力简便。由算例3、算例4、算例5可知，采用转置矩阵求解空间静不定杆系内力，要比数学微分法研究静不定空间桁架的内力更简便。所以，采用转置矩阵研究静不定杆系的内力求解，比其它方法具有简洁、清晰的优点，更易于学生和工程设计人员掌握和应用。

5 结 论

(1)采用转置矩阵求解静不定杆系内力，利用静力平衡方程可以得到杆系内力矩阵，而杆系内力矩阵与位移矩阵是互为转置矩阵，这样在得到静不定杆系的变形协调条件后，即可方便地求得静不定杆系的内力。

(2)采用转置矩阵求解静不定杆系内力，比采用拉格朗日函数法研究静不定结构内力简便，比采用数学微分法研究

静不定空间桁架的内力更简便。

(3)当静不定杆系内、外力平衡关系较容易确定，而静不定杆系的变形协调条件难以确定时，采用转置矩阵可以方便求得静不定杆系内力，其计算过程简洁、清晰、明了，与其它方法相比具有简洁、清晰的优点，更易于学生和工程设计人员掌握和应用。