基于遗传算法的双曲柄伺服压力机杆系的优化设计

项余建，汤世松，周智伟，佘 宽，刘 志

（扬力集团股份有限公司，江苏 扬州 225127）

基于遗传算法的双曲柄伺服压力机杆系的优化设计

项余建，汤世松，周智伟，佘 宽，刘 志

（扬力集团股份有限公司，江苏 扬州 225127）

双曲柄伺服压力机具有低速急回和增力的特性。通过双曲柄杆系模型的建立，借助语言编程工具，利用遗传算法，进行单目标优化设计。据此设计了双曲柄杆系参数，分析了滑块位移、速度、加速度以及大齿轮所需转矩曲线。有效降低了伺服电机功率，为大吨位伺服压力机的设计提供一定的理论计算基础。

伺服压力机；伺服电机；双曲柄；低速急回；单目标；优化设计；遗传算法

伺服压力机具有优质的成形能力、优越的生产效率、优良的设备安全性以及节能环保等特点。自上世纪90年代问世以来，得到快速发展，日本、欧美等国伺服压力机所占比例已经达到25%～40%。近年来，国内在伺服压力机开发研制方面加大了投资力度，推出了不同规格、不同传动形式的伺服压力机。但总体来说，国内伺服压力机研发的市场化进程较慢，至今未见批量推入市场的报道。究其原因，除在技术上尚需继续成熟完善之外，还由于伺服压力机是依靠伺服电机的瞬时扭矩提供压制力，其电机功率需比普通压力机电机功率大得多。因此，大功率伺服电机的性能和价格是制约我国伺服压力机市场化的关键因素。如何减小伺服电机的功率需求，降低制造成本和市场价格，是国内伺服压力机开发首要考虑的问题。

1 双曲柄杆系模型的建立

为了使伺服压力机滑块既可获得下行程转角大、返程转角小的急回特性，又可得到滑块下死点附近优良的成形曲线和显著的增力作用，需要建立双曲柄杆系模型，该机构的各个几何和运动参数如图1所示。

在双曲柄杆系机构中，已知输入杆3（L3）转角α3和角速度ω3，可计算得到铰接点C坐标

图1 双曲柄杆系模型

以及铰接点B坐标

由（2）式进一步推导出输出杆L1转角α1和连杆L2转角α2

输出杆L1角速度

输出杆L1角加速度

由输出杆L1转角、角速度和角加速度，便可求解滑块位移s、速度v和加速度a。如下所示：

式中：R为曲柄半径；k为连杆5系数；α1为曲柄转角。

根据能量守恒定理，传动系统的输入功率和输出功率的代数和为零，在不考虑摩擦转矩的条件下，作用在滑块上的负载Q与滑块速度v的乘积等于输入杆L3的转矩M与其角速度ω3的乘积，即：M·ω1=Q·v，则输入杆转矩M为：。

由式（1）～（5）可见，双曲柄机构输出杆 1 转角 α1与输入杆3转角α3存在非线性关系，在输入杆3匀速ω3转动的条件下，其输出杆1转速ω1为非匀速。因此，通过合理选择双曲柄杆系参数，可得到理想的滑块位移s、速度v和加速度a。

2 遗传算法的优化设计

由上述分析可见，双曲柄杆系结构参数对压力机滑块的位移、速度、加速度以及作用在输入杆上的转矩影响较大，需要对杆系参数进行优化设计。遗传算法是借用生物遗传学自然选择、遗传、交叉、变异等作用机制，可获得全局最优解的最新优化方法。

对双曲柄杆系结构参数进行遗传算法优化，其优化模型为：设计变量 X=[x1，x2，x3，x4，x5]，分别为双曲柄杆系的杆长 L1、L2、L3、L4以及杆 L1与曲柄轴的相位角Φ。建立目标函数minF（X），可进行单目标优化，这里以滑块位于公称力行程处，作用在双曲柄杆系输入杆3的转矩最小为目标函数，即：

约束条件：双曲柄杆系存在条件；最小传动角条件；杆系干涉条件；滑块max（v）限制条件；滑块max a）限制条件；杆系参数上下限条件；滑块急回特性条件。

利用语言编程工具编写双曲柄杆系参数优化数学模型以及相应的遗传算法功能模块，并设置优化设计遗传算法初始种群数（50～100）、交叉概率（0.6～0.8）、变异概率（0.01～0.1）、遗传代数（100～200）等优化过程参数，根据冲压工艺要求设置约束条件参数，进行双曲柄杆系参数优化，即求得不同约束条件下满足目标函数的全局最优双曲柄杆系参数L1、L2、L3、L4以及 Φ。举例说明，对于 4000kN 单点伺服压力机，选择初始种群数80，交叉概率0.7，变异概率0.05，遗传代数100，经过遗传算法优化得到杆系参数 为 ：L1=280mm，L2=360mm，L3=430mm，L4=160mm，Φ=20°。图2～5分别为优化前后杆系参数下的滑块位移、速度、加速度以及输入杆3转矩与输入杆3转角的关系曲线图。

图2 位移

图3 速度

图4 加速度

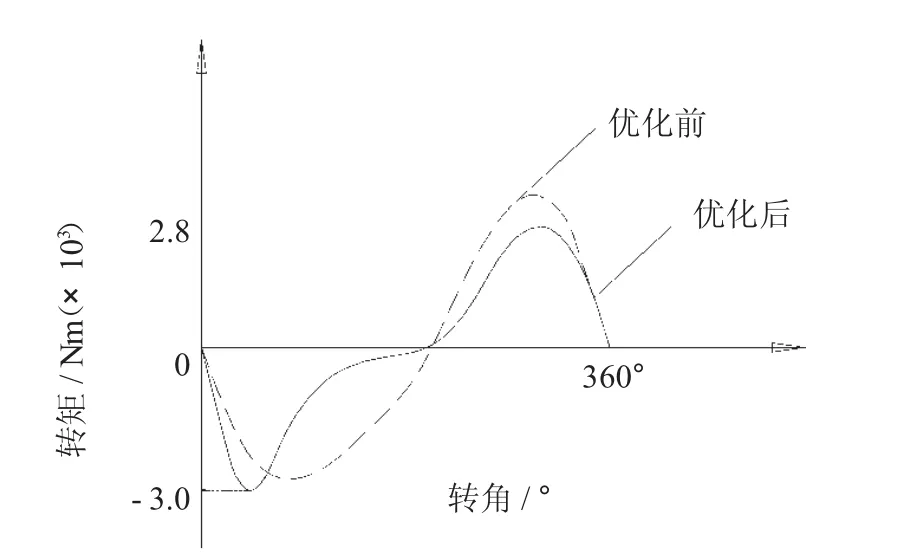
图5 转矩

3 结论

双曲柄伺服压力机双曲柄杆系参数是整个压力机的重要组成部分，是实现滑块快速空程、低速冲压和快速回程功能的基础。本文通过借助于编程语言，利用遗传算法进行单目标优化设计了双曲柄杆系参数，降低了杆系参数设计的盲目性，提高了设计效率。优化后的曲线显示具有低速急回和增力特性，有效降低伺服电机功率，达到预期目的。

[1]范宏才.现代锻压机械[M].北京：机械工业出版社，1994.

[2]赵升吨，何予鹏，等.双曲柄串联低速急回机构及其遗传算法优化[J].西安交通大学学报，2005，（9）：913-916.

[3]李长河，毕晓伟，等.高速压力机下死点动态精度稳定技术[J].新技术新工艺，1999，（2）：15-16.

[4]林伟庆，李振石，等.基于遗传算法的多连杆压力机运动优化方法[J].锻压技术，2011，（10）.

[5]汤世松，项余建，仲太生，等.精密智能型伺服压力机运行模式分析[J].锻压装备与制造技术，2016，51（2）：50-53.

[6]何德誉.曲柄压力机[M].北京：机械工业出版社，1981.

[7]莫健华，郑加坤，古闲伸裕，等.伺服压力机的发展现状及其应用[J].锻压装备与制造技术，2007，42（5）：19-22.

[8]叶春生，莫健华，樊自田，等.曲柄连杆伺服压力机控制模型的研究及系统实现[J].锻压装备与制造技术，2009，44（5）：53-56.

[9]项余建，汤世松，仲太生，等.精密型伺服压力机下死点精度控制技术的研究[J].锻压装备与制造技术，2016，51（1）：54-57.

Optimal design of rod system for double crank servo press on the basis of genetic algorithm

XIANG Yujian,TANG Shisong,ZHOU Zhiwei,SHE Kuan,LIU Zhi
（Yangli Group Co.,Ltd.,Yangzhou 225127,Jiangsu China）

Double crank servo press has the characteristics of low speed quick return and increasing force.Through the establishment of double crank rod system model,with the help of programming tools and genetic algorithms,the double crank rod system parameters have been designed for the single objective optimization.The slider displacement,velocity and acceleration have been analyzed,as well as the required torque curve of the big gear.The power of the servo motor has been effectively reduced.It provides certain theoretical calculation basis for the design of large tonnage servo press.

Servo press;Servo motor;Double crank;Low speed quick return;Single target; Optimal design;Genetic algorithm

TG315.5

A

10.16316/j.issn.1672-0121.2017.03.002

1672-0121（2017）03-0017-03

撤稿声明

《锻压装备与制造技术》编辑部

2017-01-20；

2017-03-05

项余建（1981-），男，工程师，从事伺服压力机及自动化控制方向研究。E-mail：xiangjianyuaoz@163.com

《锻压装备与制造技术》2017年第一期发表的论文“现代自由锻造装备技术研究与发展”，作者牛勇、权晓惠、张营杰、李淼泉，现因故撤稿。特此声明。