一类非连续治疗饱和传染率的传染病模型研究

陶龙,赵妍

(皖南医学院 公共基础学院,安徽 芜湖 241000)

人类发展的历史上伴随着诸多和传染病抗争的事例,数学家通过总结经验提出了依靠数学模型进行定性和定量研究。其中影响最深远的则是Kermack和Mckendrick共同提出的传染病仓室模型[1],并以此为依据揭开了17世纪横行欧洲的黑死病的客观规律。时至今日,数学家们借助于仓室模型得到了一系列关于传染病的丰硕成果[2－4]。文献[5]研究了一类具有非线性传染概率的病毒仓室模型,文章通过构造恰当的Lyapunov函数,证明了模型的地方病平衡点和无病平衡点的存在唯一性以及全局收敛性。然而美中不足的是,大部分传染病模型只考虑了连续的免疫过程,即只建立了连续的微分方程来进行病毒传染的研究,这是不够准确的。病毒传染的初期,人们还没有意识到病毒感染的相关问题,导致人们没有及时治疗甚至是忽略了治疗。而经过一段时间后,当人们意识到问题的严重性,便会突然加大免疫治疗的力度,导致病毒数量发生跳跃性的改变。因此整个病毒治疗的过程其实更接近于一个非连续的变化过程。类似的非连续模型研究也广泛地应用于力学、神经网络科学和生物学领域[6－8]。此外,文献[5]假设病毒感染能力是无限大的,而现实中已被感染的个体单位时间内接触其它个体的能力是有限的。因此病毒的传染率不可能随着被感染个体的规模的无限增大而增大,应是逐渐趋向于一个饱和状态的过程。基于以上考虑,本文创立如下模型,以更适应现实中的传播规律。

1 模型的描述

我们提出如下的微分方程模型:

其中:h(I)是非连续免疫项,表示感染体免疫的能力,α1f(I)为暂时的免疫概率,且有α1＞0,f连续可微,f′≥0,f(0)＝1;(S,I,R)的初值为;模型(1)的基本再生数[5]为:

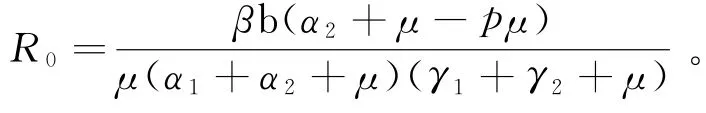
为了保证模型的一般性,故提出假设1:

假设1h(I)＝φ(I)I,φ:R＋→R＋的非单减函数,且在函数的每一个紧致区间内至多有有限个跳跃间断点。

由于(1)式的右端存在非连续项h(I),故经典的微分方程理论不能在这里应用。为了解决这个问题,我们引入Filippov解[9]。Filippov解考虑的是这样的一类非连续微分方程:

若向量函数(S(t),I(t),R(t)),t∈(0,T],T∈(0,∞]在[0,T)的任何子区间[t1,t2]上都是绝对连续的,且对几乎所有的t∈(0,T],(S(t),I(t),R(t))都满足下面的微分包含:

其中m(t)满足如下条件:

1)m(t)是除[0,T)内一系列零测度集以外的,由(S(t),I(t),R(t))唯一确定的测度函数;

2)m(t)存在当且仅当(S(t),I(t),R(t))对所有的t∈(0,＋∞)都连续可微。

2 平衡点的存在唯一性

2.1 解的正定性和有界性

下面将证明模型(1)平衡点的存在唯一性,在证明之前我们需要说明模型满足初值条件的解具有正定性和有界性,故提出下面的引理1:

引理1若假设1成立,如果(S(t),I(t),R(t))是模型(1)满足初值条件(S(0),I(0),R(0))＝(S0,I0,R0)∈R3

＋的解,则(S,I,R),t∈(0,T)是有界的。

2.2 平衡点的存在唯一性

因此,对于平衡点的存在唯一性有如下结论:

引理2 若R0＞1,则微分包含(6)式存在唯一正解且有:

一、当代雕塑观念的变异性和先锋观，直接依附本体语言方可“拨苗助长”。除了意识高度和品质境界以及形态外，最直接的“快感”，通过具有阻断力和颠覆性的媒材来完成思考的更移。

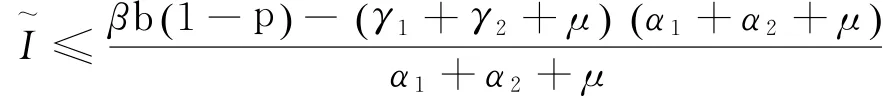
证明：∵R0＞1,∴g(0)＞φ(0)＞0,又函数g(I)是单调递减的函数,φ(I)是关于I的非单减函数。此外,g(I)≤0当且仅当:

则集合{I:g(I)≥φ(I＋),I＞0}有界,

3 有限时间的全局收敛性

为了证明模型(1)的全局收敛性,我们先做以下假设:

假设2 若R0＞1,则φ(I)在I*处会有一跳跃间断点,同时I*是由引理2唯一确定的正解且:由假设2可定义:θ＝min{φ＋(I*)－ξ*,ξ*－φ－(I*)}＞0。

定理1若假设1和 假设2均成立,模型(1)的解都将在有限时间内全局收敛于地方平衡点E*＝(S*,I*,R*),即当t＞t*时,有(S,I,R)＝(S*,I*,R*),t∈(0,＋∞)。其中:

最后我们来证明模型(1)在有限时间内也全局收敛于无病平衡点。由于假设1假定了h(I)在I＝0处是连续的,因此不满足模型无病平衡点是非连续的条件。故需如下假设:

假设3若h:R＋→R＋是非单调的递减函数,且在可行区域的每一个紧致区间内至多有有限个跳跃间断点,同时h(0)＝0但在I＝0处不连续。

定理2若假设3成立,当R0＜1时,模型(1)所有满足初值条件的解都将在有限时间内全局收敛于无病平衡点:

4 Matlab数值模拟仿真

4.1 地方病平衡点的全局收敛性

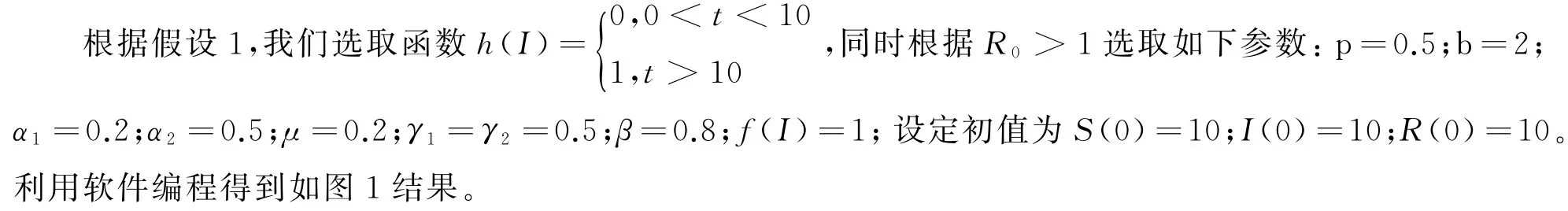
通过图1发现:S,I,R的节点各自在经过一段时间的免疫治疗后趋向平衡状态。

图1 地方平衡点的变化趋势图

4.2 无病平衡点的全局收敛性

利用软件编程得到如图2结果。

通过图2发现:S,R节点在各自经过一段时间的治疗后到达平衡状态,已感染的I类节点经过一段时间的治疗后变为0。

图2 无病平衡点的变化趋势图

5 结论

5.1 通过对非连续治疗的传染病模型研究,发现满足模型初值条件的所有解都能够在有限时间内趋于平衡点,有限时间稳定这一点具有重要的现实意义,因为已经感染病毒的个体和感染疾病的患者都希望知道自己的病情能否被治愈,或者希望知道病情将会在何时稳定或被治愈。

5.2 数值仿真验证了本文理论推导结果的正确性和可行性,同时也说明利用微分包含的相关知识可以较好地解决具有非连续性免疫治疗策略的动力学问题,由此可将非连续的想法推广到其他动力学领域中[13－15],通过建立更加符合现实变化规律的微分方程,从而得到更加符合实际生活情况的结果。