考虑天然气系统初值优化的综合能源系统改进多能流计算方法
王舒萍,张沈习,程浩忠,原 凯,宋 毅,韩 丰
(1. 上海交通大学电力传输与功率变换控制教育部重点实验室,上海 200240;2. 国网经济技术研究院有限公司,北京 102209)
0 引言
随着我国碳达峰和碳中和等战略目标的提出,如何建设清洁高效的能源系统、促进能源高质量发展成为研究的重点[1-2]。综合能源系统(IES)实现了电、气、热等多种能源的耦合互联和互补互济,为实现能源的综合管理和调控、提高能源利用效率、构建低碳可持续能源系统提供了新的途径[3-4]。而实现IES 多能流的有效计算和分析是其他相关研究的基础,对研究协同规划、运行优化和经济调度等具有重要意义[5]。目前,针对IES 多能流计算,国内外研究主要集中在模型建立和算法求解2个方面。
在IES多能流建模方面:文献[6-7]建立了电力、天然气和热力网络的能流模型,并在此基础上构建了IES 多能流计算模型;文献[8]从模型精细化程度和耦合环节的数学表达式出发,将IES 多能流计算模型分为5 类并分别介绍;文献[9]构建了电-气互联IES 稳态分析综合求解模型,并通过能源集线器模型描述其能源耦合环节;文献[10]同样建立了电-气互联IES能流计算模型,研究了风电出力不确定性对天然气系统稳态运行的影响;文献[11]提出了适用于分布式气源注入的天然气系统能流分析方法;文献[12]建立了热力网络的水力模型和热力模型,在此基础上构建了电-热互联IES多能流计算模型。
在IES 多能流求解算法方面,目前仍主要基于牛顿-拉夫逊(NR)法进行求解,从IES不同子系统能流方程是否联立求解的角度出发,可将其分为统一求解法和分解求解法。文献[13-14]针对电-热互联IES 多能流问题分别采用统一求解法和分解求解法进行了计算;文献[15]提出了分别适用于IES 完全解耦、部分耦合以及完全耦合3 种运行模式的混合潮流求解算法;文献[16]提出了快速解耦的IES 多能流计算方法,将NR 法的雅可比矩阵转化为对角常数雅可比矩阵,提高了算法求解效率。还有学者在提高多能流算法收敛性上进行了一定研究[17-19]。文献[17]针对NR 法对初值较为敏感这一不足之处,提出了基于自适应步长因子的改进统一法;文献[18]提出采用牛顿下山法对多能流模型进行求解,以改善算法的收敛性;文献[19]通过遗传算法(GA)优化天然气系统初值,提出了电-气互联IES 多能流计算的改进方法。
上述研究表明,IES多能流计算已受到国内外学者的广泛关注,但仍普遍存在以下问题:在电力系统和热力系统的初值较容易给定的情况下(通常可采取平启动方式),天然气系统的压力初值变化范围相对较大,尤其是对于含有环状管网的天然气系统,其气流方向无法提前预知,而平启动方式会使得雅可比矩阵奇异[7],导致天然气系统压力初值难以给定,而传统的NR 法对初值较为敏感,容易因为初值给定不理想而无法收敛。文献[7,20]也指出天然气系统初值需要谨慎选取,但目前仍缺少有效解决方法。此外,目前的研究中对多能流求解算法的收敛性与收敛速度分析较少,尤其对于IES 中规模较大且含有环状管网的天然气系统,如何给定较为理想的初值从而提高算法收敛性和收敛速度,仍需要进一步研究。
鉴于此,本文提出一种考虑天然气系统初值优化的IES 改进多能流计算方法。首先,建立了天然气系统稳态能流模型,并采用分段线性化方法对天然气管道流量方程线性化;其次,建立了基于线性管道流量方程的天然气系统初值优化模型;在此基础上,结合NR 法提出了考虑天然气系统初值优化的IES 改进多能流计算方法和计算流程;最后在2 个规模不同的IES 上进行算例仿真和分析,验证了所提方法能有效改善算法的收敛性和收敛速度。
1 天然气系统能流模型及其线性化模型
1.1 天然气系统能流模型
天然气系统由气源、输气管道和天然气负荷等部分组成。天然气由1 个或多个气源供应,经过高、中、低压输气管网传输到负荷点。
天然气系统的管道流量连续性方程为:

式中:Sg为节点的气源注入流量向量;Lg为节点的负荷流量向量;Ag为天然气网络的节点-支路关联矩阵;fg为管道流量向量。
不同压力等级的天然气系统管道流量方程有所不同。对于中高压输气管道,采用Weymouth方程[11]来描述管道流量与两端气压的关系,具体表达式为:

式中:Cij,D为低压输气管道的气流传输参数,与管道长度、管道直径、气体比重等有关。
1.2 天然气系统线性化能流模型
上述天然气系统能流模型中的非线性项仅存在于天然气管道流量方程。对于中高压输气管道流量方程,将式(2)中的气压平方项用变量Π替换,且式(2)中的αij f2ij转化为fij|fij|,由此可得:

此时式(5)中的非线性项仅为等号左侧的fij|fij|。记y=fij|fij|,采用分段线性化方法[21]将其线性化处理,分段线性化示意图如附录A图A1所示。
分段线性化的具体步骤包括:首先确定线性化分段区间和分段段数nl;然后选取离散点fij,0、fij,1、…、fij,nl;最后引入非负变量δij,k和二进制变量zij,k,得到线性的天然气管道流量方程如式(6)—(11)所示。

低压输气管道流量方程的线性化方法和步骤与中高压相同,不同的是,低压输气管道流量方程中不含气压平方项,因此不需要进行变量替换。线性化后的低压输气管道流量方程包括式(7)—(12)。

2 考虑天然气系统初值优化的IES改进多能流计算方法
2.1 天然气系统初值优化模型
NR法对初值的依赖性较高,而初值状况对算法的收敛性和收敛速度有着较大影响;电力系统和热力系统的初值较容易给定,而天然气系统的初值给定尚缺少有效方法。因此,本节建立天然气系统初值优化模型,以此获得优良的初值。
2.1.1 目标函数
考虑到天然气系统能流模型的本质为各个节点的流量平衡方程,可设置天然气系统初值优化模型的目标函数为所有节点流量不平衡量的平均值Fg最小[19],如式(13)所示。

式中:ng为天然气系统节点总数;ΔFg,i为节点i的流量不平衡量,其表达式如式(14)所示。

2.2 IES多能流计算模型
本文后续将重点研究天然气系统初值优化对IES多能流求解算法收敛性及收敛速度的影响,为建立IES 多能流计算模型,做出如下基本假设:①忽略不同能源子系统在时间尺度上动态特性的差异,各能源子系统均采用稳态模型;②采用能源集线器模型描述不同能源子系统之间的耦合关系;③构建多能流统一求解计算式,采用基于NR 法的统一求解法进行求解。
2.2.1 电力系统潮流模型
电力系统采用经典的交流潮流模型,极坐标下的潮流方程为:
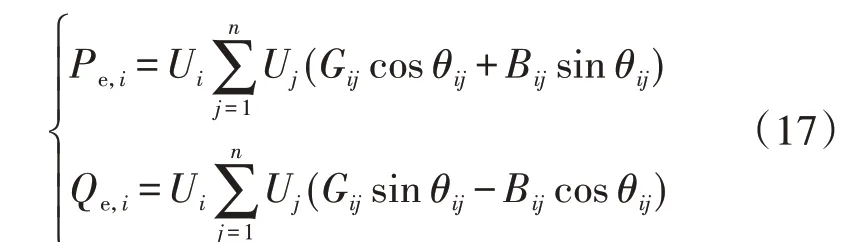
式中:Pe,i和Qe,i分别为节点i的注入有功功率和注入无功功率;Ui和Uj分别为节点i和j的电压幅值;Gij和Bij分别为节点导纳矩阵中第i行第j列元素的实部和虚部;θij为节点i和j的电压相角差;n为电力系统节点数。
2.2.2 天然气系统能流模型
天然气系统能流计算模型采用原始的非线性模型,具体见式(1)—(4)。
2.2.3 热力系统能流模型
热力系统能流模型包括水力、热力模型两部分。
1)水力模型。
热水在管网中流动需满足流量连续性方程和回路压降方程:

式中:Ah为热力网络的节点-支路关联矩阵;m为管道流量向量;mq为节点注入流量向量;Bh为热力网络的回路-支路关联矩阵;hf为压头损失向量,其计算表达式如式(20)所示。

式中:K为管道阻力系数矩阵。2)热力模型。
热力模型包括节点热功率方程、管道温度降落方程和节点混合温度方程,分别如式(21)—(23)所示。

式中:Φ为节点注入热功率向量;Cp为水的比热容;Ts为节点供热温度向量;To为节点输出温度向量;Tend为管道末端温度;Tstart为管道首端温度;Ta为环境温度;λ为管道热传导系数;L为管道长度;m为管道流量;mout、min分别为流出、流入节点的热水流量;Tout、Tin分别为流出、流入节点的热水温度。
2.2.4 能源集线器模型
对于涉及电力、天然气和热力3 种能源的能源集线器,其输入与输出关系可表示为[15]:

式中:下标e、g 和h 分别表示电力、天然气和热力;LEH为能源集线器的负荷功率向量,Le、Lg和Lh分别为能源集线器的电负荷、天然气负荷和热负荷;CEH为能源集线器的耦合关系矩阵,Cee为电力向电力转换的转换系数,Ceg为电力向天然气转换的转换系数,其余矩阵元素定义类似;PEH为能源集线器的输入功率向量,Pe、Pg和Ph分别为能源集线器的输入电功率、输入天然气功率和输入热功率。
2.2.5 IES稳态多能流计算模型
综合上述4类稳态模型,构建含电、气、热3种能源的IES 多能流计算模型[22]如式(25)所示。式中第1、2行描述电力系统潮流;第3行描述天然气系统能流,其中天然气管道流量方程为原始的非线性方程;第4—7 行描述热力系统能流;第8 行描述能源集线器的能源转换关系。
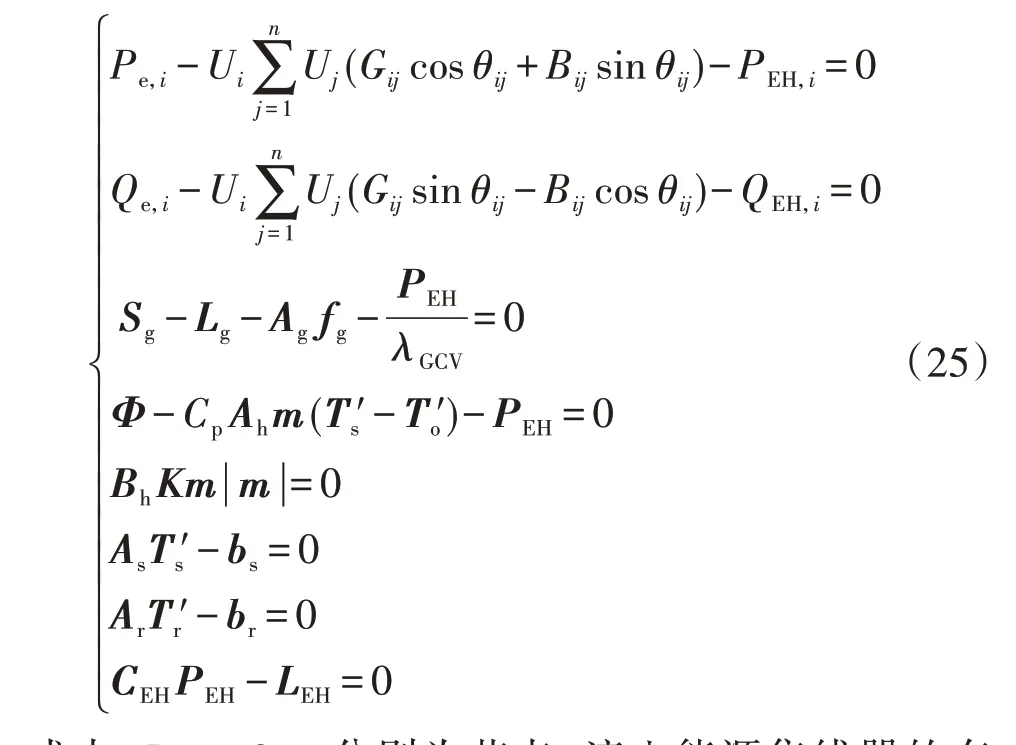
式中:PEH,i、QEH,i分别为节点i流入能源集线器的有功、无功功率;λGCV为天然气热值;T′s、T′o和T′r分别为供热、输出和回热温度减去环境温度得到的温度向量;As、Ar分别为与供热网络、回热网络的结构和流量有关的矩阵;bs和br分别为与供热温度、回热温度有关的向量。
2.3 IES多能流统一求解法
在进行IES 多能流求解之前,需要先对电力系统、天然气系统和热力系统的节点进行分类,以明确每个节点的已知变量与待求变量。IES 节点类型如附录A表A1所示。
采用基于NR 法的统一求解法对式(25)所示的IES多能流计算模型进行求解,具体迭代公式为:

式中:对角块Jee、Jgg、Jhh和JEHEH分别为电力系统、天然气系统、热力系统和能源集线器不平衡量对自身状态变量求偏导形成的雅可比矩阵;非对角块Jeg表示电力系统不平衡量对天然气系统状态变量求偏导形成的雅可比矩阵,其余非对角块定义类似。
2.4 考虑天然气系统初值优化的IES改进多能流计算流程
综上,提出考虑天然气系统初值优化的IES 改进多能流计算流程,其主要包含两步:①建立天然气系统初值优化模型以获得优良的初值,优化模型中采用线性化后的管道流量方程以简化模型复杂度;②采用基于NR 法的统一求解法对IES 多能流计算模型进行求解,其中天然气系统初值采用优化后的初值。IES改进多能流计算流程如图1所示。
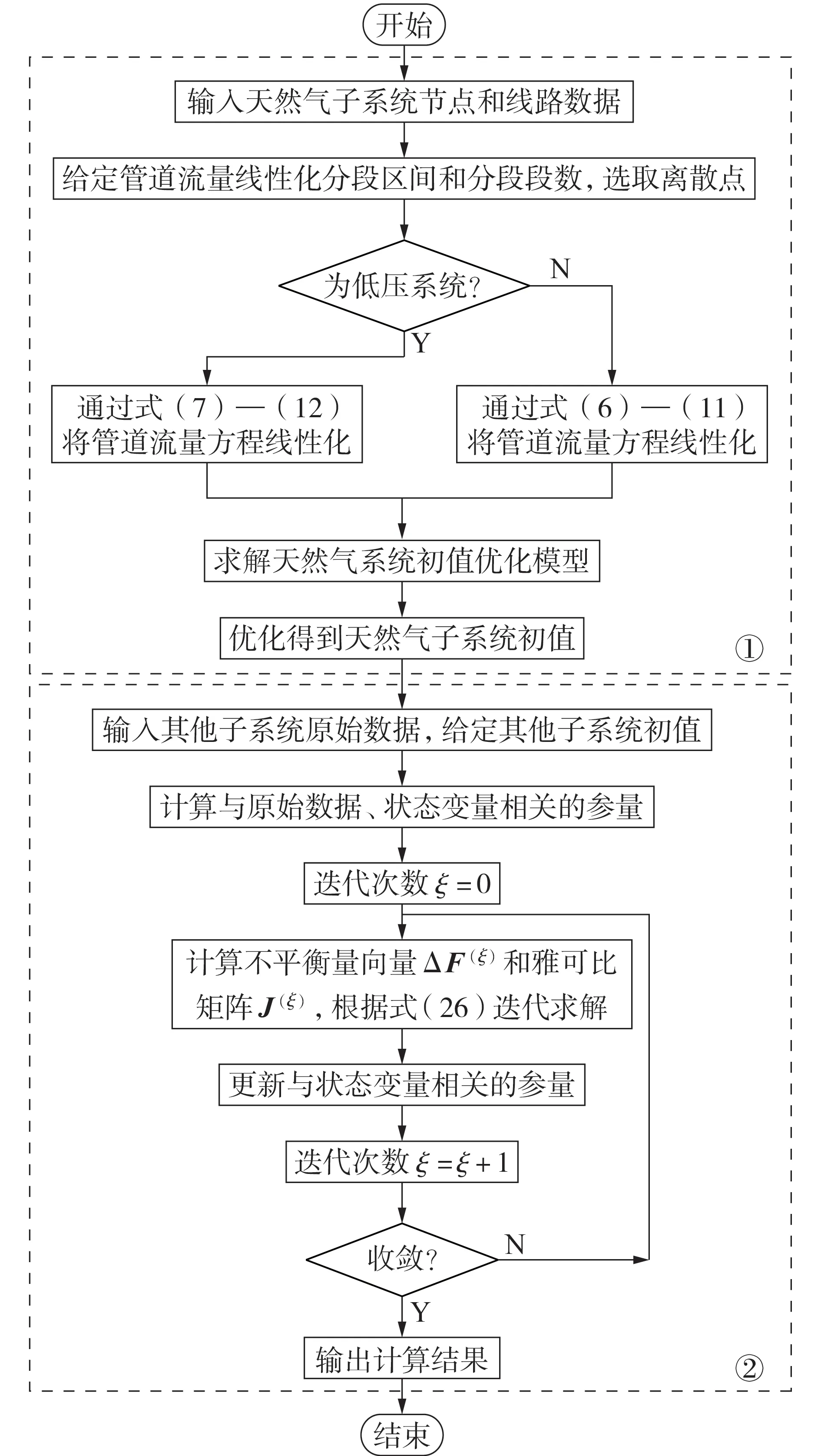
图1 考虑天然气系统初值优化的IES改进多能流计算流程Fig.1 Flowchart of improved multi-energy flow calculation for IES considering initial value optimization of natural gas system
3 算例分析
本文算例均在CPU为Inter(R)Core(TM)i5-7400、主频为3 GHz 的测试环境下通过MATLAB R2018b进行计算。为验证本文所提算法的有效性,选取以下5 种算法分别进行多能流计算并比较其计算性能。
算法1:常规基于NR法的统一求解法(以下简称NR法)。
算法2:将多能流计算问题建模为以系统所有节点不平衡量总和最小为目标的非线性非凸优化问题,并通过转凸及近似方法将原优化问题转化为凸优化问题COP(Convex Optimization Problem),直接优化得到多能流结果(以下简称COP法)。
算法3[19]和算法4:分别通过GA 和内点法IPM(Interior Point Method)对天然气系统初值进行优化,再通过基于NR 法的统一求解法计算IES 多能流。其中天然气系统初值优化模型的目标函数与式(13)相同,约束条件同样包括天然气管道流量方程约束、气压约束和气源注入流量约束,但算法3(以下简称GA-NR 法)和算法4(以下简称IPM-NR 法)中采用原始的非线性管道流量方程。
算法5:本文所提的考虑天然气系统初值优化IVO(Initial Value Optimization)的IES 改进多能流计算方法(以下简称IVO-NR法)。
此外,考虑到程序运行时间的波动性及其他随机性因素,本文对算例每种情况下的多能流均求解50次,统计求解效果的平均水平。
3.1 算例1
3.1.1 算例概况
算例1 为IEEE 33 节点系统与天然气11 节点系统、热力32 节点系统经2 个能源集线器耦合而成的IES,系统拓扑结构图见附录B 图B1。其中,电力系统的平衡节点为EB1,其余节点为PQ 节点;天然气系统平衡节点为GB1,其余节点为负荷节点;热力系统平衡节点为HB1,节点HB31、HB32为热源节点,其余节点为负荷节点。天然气系统参数详见文献[11];热力系统参数详见文献[23]。
3.1.2 算法性能评估
1)NR法性能。
NR法中天然气系统初值设定采取如下方法:由于算例1 中天然气系统为环网,无法提前预知所有管道气流方向,因此节点气压初值设置为固定区间范围内的随机数。表1 为不同初值范围条件下NR法的收敛性与收敛速度。设天然气系统气源气压为p,表1中[0.90p,p]表示天然气系统节点气压初值设置为[0.90p,p]内的不同随机数,其他天然气系统节点气压初值范围的定义类似。

表1 不同初值范围条件下NR法收敛性与收敛速度Table 1 Convergence and convergence rate of NR method with different initial value ranges
由表1 可知,当采用NR 法计算多能流时,随着天然气系统节点气压初值给定区间逐渐增大,算法的收敛性逐渐变差,NR 法迭代次数增多,求解时间也逐渐变长。分析其原因为:本算例天然气系统节点气压值均处在[0.90p,p]范围内,因此随着天然气系统节点气压初值范围从[0.90p,p]逐渐扩大到[0.60p,p]时,初值离真实值偏离程度逐渐增大,因此NR法迭代次数逐渐增多。表中数据也说明了NR法对初值依赖性较高,容易出现因为初值给定不理想而不收敛的情况。
2)COP法性能。
COP法将多能流计算问题建模成以系统所有节点不平衡量总和最小为目标的优化问题,同时电力系统引入二阶锥松弛法,天然气系统采用1.2节的分段线性化方法,热力系统采用基于McCormick 法的分段松弛方法[24],将原优化问题转化为凸优化问题。天然气系统管道流量线性化分段数用N1表示,热力系统凸松弛分段数用N2表示,N1、N2取值不同时所对应的COP 法求解时间如附录B 图B2 所示。此外,由于COP 法求解得到的多能流结果为近似解,选用相对误差指标[22]衡量结果的准确性,其中以NR 法计算得到的多能流结果作为基准值。N1、N2取值不同时天然气系统节点气压和热力系统节点供水温度的平均相对误差如表2所示。

表2 N1、N2取值不同时节点气压、供水温度平均相对误差Table 2 Average relative error of node pressure and water supply temperature with different values of N1 and N2
通过附录B 图B2 可以看出,对于本算例COP 法求解时间大体在5~8 s之间,随着N1、N2取值的增大,COP 法求解时间基本上也是逐渐增大的趋势,且N2取值对求解时间的影响稍大。进一步由表2 可知,N1、N2取值越大,节点气压和节点供水温度的平均相对误差越小,多能流计算结果越准确,但牺牲了一定的计算时间。
3)GA-NR法与IPM-NR法性能。
GA-NR 法中GA 相关设置如下:种群规模为200,进化代数为100,遗传算子包括选择、交叉和变异,采用轮盘赌选择算子来保留优秀个体,以单点交叉和自适应变异方式来产生新的种群。设IPM-NR法中内点法的终止条件为迭代步长小于10-6。不同节点气压约束上下限情况下GA-NR 法与IPM-NR 法的收敛性与收敛速度如附录B表B1所示。
由表B1 可知,随着节点气压约束范围的扩大,GA-NR 法与IPM-NR 法收敛率逐渐减小,迭代次数逐渐增大,求解时间逐渐增加;相比NR 法,算法的收敛性有所改善但依旧不够稳定。若想通过GA 或内点法优化得到较好的天然气系统初值,则节点气压约束上下限需接近于节点气压真实值;若节点气压约束范围过大或偏离真实值较远,则会出现天然气系统初值优化结果不够理想从而使得GA-NR 法与IPM-NR 法无法收敛的情况。而在实际情况中很难提前预知节点气压的精确范围,限制了算法的进一步应用。但相比GA-NR 法,IPM-NR 法在求解时间和收敛率上均体现出更好的性能,说明对于本文的天然气系统初值优化问题而言,内点法寻优能力优于GA。
4)IVO-NR法性能。
设置固定的管道流量线性化区间,在此区间分别设置线性化分段段数为2—10段,IVO-NR法收敛率均为100%。不同线性化分段段数下IVO-NR 法的收敛性与收敛速度如图2所示。
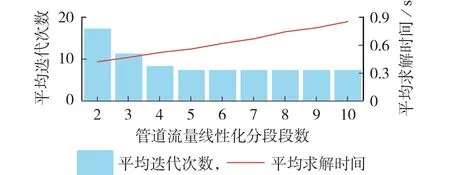
图2 不同线性化分段段数下IVO-NR法收敛性与收敛速度Fig.2 Convergence and convergence rate of IVO-NR method with different numbers of linearization segment
由图2 可知:当线性化分段段数逐渐增加时,优化得到的天然气系统初值愈发精确,IVO-NR法迭代次数逐渐减少,平均求解时间增加;但当线性化分段段数达到一定限值(本算例中为5 段)时,再增加线性化分段段数已无法使算法平均迭代次数减少,但求解总时间仍然继续增加。由此可以说明,对于本算例,采用分支定界法求解天然气系统初值优化模型时消耗时间相对较长,导致初值优化消耗的时间占求解总时间比例较大,求解总时间与线性化分段段数成正比。总体而言,IVO-NR 法性能较为稳定,算法收敛率不受线性化分段段数的影响;若想减少算法求解时间可以选择尽可能小的线性化分段段数。与NR 法相比,虽然初值优化消耗的时间导致求解总时间有所增加,但解决了天然气系统初值难以给定的问题,改善了算法的收敛性。
5)不同负荷水平下5 种算法的收敛性与收敛速度对比。
设置不同的负荷水平,各节点负荷量分别为原始负荷量的1/1.4、1/1.2、1 倍、1.2 倍和1.4 倍,验证5种算法的收敛性与收敛速度。对于NR 法中天然气系统的初值设定,参考表1 所示结果,设置天然气系统节点气压初值为[0.90p,p](效果最好的区间)内的不同随机数。对于COP 法,参考附录B 图B2 及表2所示结果,选择N1、N2取值均为10。对于GA-NR法和IPM-NR 法,参考附录B 表B1 所示结果,设置节点气压约束上、下限分别为p、0.90p(效果最好的上、下限)。对于IVO-NR 法,不同负荷水平下,设置与负荷水平成正比的管道流量线性化区间,参考图2 所示结果,设置线性化分段段数均为2 段。不同负荷水平下5 种算法的收敛性与收敛速度对比如附录B表B2所示。
由附录B 表B2 可知,不同负荷水平下NR 法迭代次数和求解时间有所波动,当负荷量与初始负荷量的比值为1/1.4 和1/1.2 时,NR 法收敛率无法达到100%。说明NR 法的收敛情况不稳定,容易受负荷水平和初值给定情况的影响。此外,不同负荷水平下COP法求解时间波动不大,均在9~10 s之间,求解时间相比其他4 种算法较长,求解效率不高,且随着负荷水平提高,天然气系统节点气压和热力系统节点供水温度的平均相对误差也逐渐增大。
同时通过附录B 表B2 可以看出,不同负荷水平下GA-NR 法、IPM-NR 法与IVO-NR 法的收敛率均为100%,算法收敛性得到改善,但IVO-NR法的平均求解时间小于GA-NR 法与IPM-NR 法,求解效率更高,且GA-NR 法与IPM-NR 法只有在节点气压约束范围接近于节点气压真实值时才会有较好的性能。相较于GA-NR 法,IPM-NR 法的性能更优。此外,对于IVO-NR 法,随着负荷水平的增大,算法迭代次数增大,平均求解时间略有增加。分析其原因为:由于不同负荷水平下所设置的管道流量线性化分段段数均为2 段,负荷水平越高时管道流量线性化区间越大,相同数量的线性化分段段数带来的近似误差越大,因此优化得到的天然气系统初值结果误差增大,算法迭代次数增加。
3.2 算例2
3.2.1 算例概况
算例2 为修改后的天津某地区IES。该系统中电力子系统包含161 个节点,节点EB1为平衡节点,节点EB35、EB55、EB116、EB153为PV 节点,其余节点为PQ 节点,总负荷为506 MW;天然气子系统包含85个节点,节点GB1为平衡节点,节点GB68、GB78为恒压源节点,其余节点为负荷节点,总负荷为27020 m3/h;热力子系统包含69 个节点,其中节点HB1为热源节点,其余节点为负荷节点,总负荷为76 MW。能源集线器与电力系统节点EB159、天然气系统节点GB13和热力系统节点HB29连接,由电力系统和天然气系统向其输入电能和天然气。
3.2.2 算法性能评估
1)NR法性能。
本算例中天然气系统也是环网,无法提前预知所有管道气流方向,节点气压初值同样设置为固定区间范围内的随机数。表3 为不同初值范围条件下NR 法的收敛性与收敛速度。由表可知,通过NR 法求解本算例多能流,仅在天然气系统节点气压初值范围[0.95p,p]时算法能够收敛但收敛率较低,平均迭代次数较多,求解时间较长。对于本算例,由于系统规模较大且难以给定较为理想的天然气系统初值,通过NR 法计算多能流时算法收敛性较差,求解效率较低。
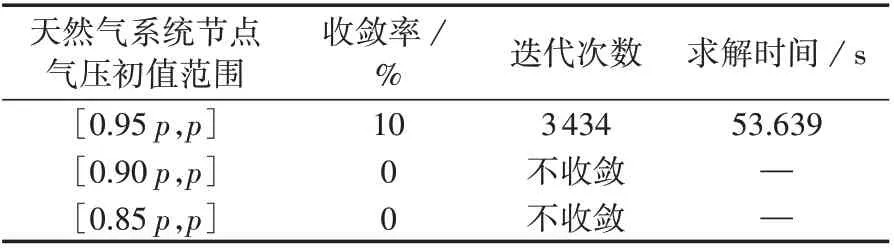
表3 不同初值范围条件下NR法收敛性与收敛速度Table 3 Convergence and convergence rate of NR method with different initial value ranges
2)COP法性能。
对于本算例,COP 法优化得到的多能流计算结果中,电力系统与天然气系统的能流计算结果尚好,但热力系统的状态变量如节点供(回)水温度、管道流量与真实值相比误差较大,参考价值较小,且算法求解时间在30 s以上,求解效率较低。分析其原因:对于热力系统能流计算模型,基于McCormick 法的分段松弛转凸方法划分段数有限,且依然存在松弛间隙,当系统规模较大时模型包含众多整型变量,求解效率低下。
3)GA-NR法与IPM-NR法性能。
GA-NR 法中GA 相关参数设置与算例1 相同。经计算,对于本算例,通过GA 优化天然气系统气压初值效果较差,导致GA-NR 法无法收敛。分析其原因为:本算例中天然气系统规模较大,含有85 个优化变量,通过GA 优化得到的结果仅是可行域内的局部最优解,目标函数值(节点不平衡量总和)由800 m3/h(初代)左右下降到500 m3/h 左右就几乎维持恒定难以继续下降,陷入“早熟”,使得优化结果不够理想。
不同节点气压约束上下限情况下IPM-NR 法的收敛性与收敛速度如附录B 表B3 所示。由表可知,与算例1 相同,IPM-NR 法的收敛性与收敛速度受气压约束范围影响较大,只有在气压约束范围接近于气压真实值时才会有较好的性能;整体而言,IPMNR 法求解时间较长,求解效率较低,但相比GA-NR法性能更优。
4)IVO-NR法性能。
设置固定的管道流量线性化区间,在此区间分别设置线性化分段段数为2—10段,IVO-NR法收敛率均为100%。不同线性化分段段数下IVO-NR 法收敛性与收敛速度具体如图3所示。

图3 不同线性化分段段数下IVO-NR法收敛性与收敛速度Fig.3 Convergence and convergence rate of IVO-NR method with different numbers of linearization segment
由图3 可知,当线性化分段段数逐渐增加时,IVO-NR法迭代次数基本呈逐渐减小趋势,而平均求解时间与线性化分段段数基本成正比。总体而言,IVO-NR法性能比较稳定,算法收敛性不受线性化分段段数的影响;若想减小算法求解时间,可以选择较小的线性化分段段数。与NR 法相比,IVO-NR 法的收敛性有较大改善,平均求解时间可由53.639 s 减少为4 s 左右,节省了大约93%的计算时间,提高了求解效率。
5)不同负荷水平下4 种算法的收敛性与收敛速度对比。
设置不同的负荷水平,各节点负荷量分别为原始负荷量的1/1.4、1/1.2、1 倍、1.2 倍和1.4 倍,验证4种算法的收敛性与收敛速度(考虑到COP 法求解效率较低,求解结果误差较大,本节不再对比)。对于NR 法中天然气系统的初值设定,参考表3 结果,设置天然气系统节点气压初值为[0.95p,p](效果最好的区间)内的不同随机数。对于IPM-NR 法,参考附录B 表B3 结果,设置节点气压约束上、下限分别为p和0.95p(效果最好的上、下限)。对于IVO-NR 法,不同负荷水平下,设置与负荷水平成正比的管道流量线性化区间,参考图3 结果,线性化分段段数均设置为8 段。不同负荷水平下4 种算法的收敛性与收敛速度对比如附录B 表B4 所示。由表可知,通过NR法求解本算例多能流时,不同负荷水平下算法收敛性均较差,NR 法平均迭代次数达上千次,求解时间较长;当负荷量与初始负荷量的比值为1/1.4 时,NR法甚至无法收敛。对于本算例,不同负荷水平下GA-NR 法均没有达到优化天然气系统初值的目的,导致算法难以收敛。相比GA-NR 法,IPM-NR 法性能更优,但求解时间仍然较长,且IPM-NR 法性能受节点气压约束范围影响较大。而IVO-NR 法不受节点气压约束范围影响,对于本算例,不同负荷水平下迭代次数均在20 次左右,求解时间减少到5 s 左右,算法性能有较大改善。
4 结论
针对传统基于NR 法的多能流求解算法对初值依赖性较强以及算法的收敛性和收敛速度难以保证的问题,本文提出了考虑天然气系统初值优化的IES改进多能流计算方法。通过2 个算例的分析验证,得到了以下结论。
1)传统基于NR 法的多能流求解算法容易因为天然气系统初值给定不理想而难以收敛,初值离真实值偏离程度越大,NR 法收敛性越差,且不同负荷水平下NR法收敛情况不够稳定。
2)本文所提的IVO-NR 法可以有效解决天然气系统初值难以给定的问题。对于规模较小的算例系统,虽然由于初值优化消耗一定时间导致算法求解时间有所增加,但提高了算法的收敛性和稳定性;对于规模较大的算例系统,相比于NR 法,不仅算法的收敛性得到较大改善,也可以节省大量的计算时间,且对负荷水平的变化具有良好的适应性。
3)本文所提算法收敛率不受线性化分段段数的影响,若想减小算法求解时间可以选择尽可能少的线性化分段段数。
在后续研究过程中,可进一步对IES 不同能源系统之间的耦合关联对多能流分布的影响进行更深入的研究,在动态能流、概率能流以及最优能流等方面也需要进行进一步研究。
附录见本刊网络版(http://www.epae.cn)。

