巧用数学几何直观 融图式于课堂说理

黄淑琼

（福建省莆田市茘城区黄石沙堤中心小学，福建莆田 351144）

引 言

著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微。”新课程理念也提出了数学教学中教师应重视对直观方法的运用，增加了“几何直观”的核心概念[1]。基于此，探索如何借助“图式相融”之法让数学高效学习在课堂上真正发生，有利于实现培养学生数学学科核心素养的目标。

一、识图助探究，明晰概念本质

数学概念是数学知识体系的基础，因此概念教学在小学数学教学中极为重要。但在具体的实践教学过程中，常有教师反映，难以找到有效的教学方法引导学生掌握概念，只能让学生对概念进行反复记忆，这导致学生很难从本质上理解概念并加以运用。正如德国科学家康德所说：“缺乏概念的直观是空虚的，缺乏直观的概念是盲目的。”教师如果在教学中可以把概念中抽象的、空泛的、静止的知识转化成形象的、动态的图示，将有利于学生对概念的理解与运用。

例如，教学人教版数学三年级（上册）“分数的初步认识”时，教师可以通过“铺垫—思辨—提升”三个环节引导学生借助图示探索分数的意义。在铺垫环节，教师可以出示一块糕点，提出要平均分给3 个同学，每个同学能分到多少？在学生答出个后，教师追问学生是怎样思考的。学生在讨论后得出结论：把一块糕点平均分成3 份，每个同学分到其中的1 份，就是。接着教师出示课件，让学生判断哪幅图可以表示刚才分糕点的情形，并说说理由（如图1）。

图1

借助“思辨”环节，学生明确了单位“1”的意义。教师课件出示第二盘食物——荔枝，让学生说说平均分给3 个学生要怎么分，学生很快就说出了“平均分”。教师和学生一起跟着课件数出一共有9 颗荔枝，学生借助图示，通过“思辨”就能得出答案：每个同学可以分到3 颗。教师追问道：“每个同学分到3 份荔枝中的1份，也就是这些荔枝的几分之几？”学生齐答。教师又问：“这次分荔枝的情境还可以用刚才的哪幅图表示呢？”学生开始思考与讨论。在讨论的过程中，教师不宜立即做出评价。思考过程后，学生会得出结论：第一次分，这个长方形表示1 块糕点；第二次分，这个长方形表示9 颗荔枝，都可以看作一个整体。教师随即抓住“整体”这个词进行小结：两次分东西，不管是1 块糕点，还是9 颗荔枝，只要是把它平均分成3 份，其中的1 份就是这个整体的。基于此，教师将分数的初步认识概念进行了提升，顺势提问：“如果第三盘有24 颗葡萄，你能画图表示它的吗？”大部分学生听完问题马上动手画图，但有一个学生举起手说可以不用画图，直接用上面的图来表示24 颗葡萄的。这位学生的回答令笔者倍感欣慰，便故作惊讶道：“这两幅图有这么神通广大吗？”师生的对话不断升级，有效揭示了数学概念的本质。

实践证明，数学概念是抽象的，要想让学生学得轻松又深刻，借助图示直观展现概念本质是行之有效的方法之一。

二、画图明题意，厘清数量关系

数学是研究数量关系和空间形式的学科，正确掌握数量关系是解决问题的关键，特别是一些行程问题的数量关系比较复杂，多数学生很难在短时间内理解题意。因此，引导和帮助学生通过画图的方式来理解知识，将有利于帮助学生厘清数量关系，找到解题的突破口。

如下面这道六年级的数学问题：

一段10 千米长的窄路，只能供一辆车通过。若两车相遇，需其中一辆车倒退到窄路一端后才能通过。一辆小汽车和一辆大卡车在这段窄路上相向行驶，相遇时，它们的路程比是3 ∶2。已知小汽车和大卡车的速度分别是40 千米/时和20 千米/时，两车倒退的速度是各自速度的，问：（1）相遇时，两车在这段窄路上各自行驶了多少千米？（2）从两车相遇到都通过这段窄路，最少需要多长时间？

这道题信息量较多，数量关系稍显复杂，大部分学生解题存在困惑，尤其是第（2）题。解答本题需要学生把数学问题“画”出来，呈现数量关系，从而降低解题难度（如图2）。这也让学生充分感受到数形结合的重要性。

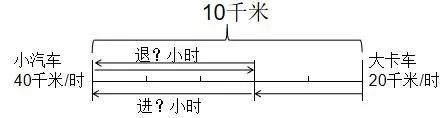
图2

通过分析线段图，学生可以看出小汽车和大卡车行驶路程占总路程的几分之几，进而列出相应的数学算式来解答第（1）题。第（2）题的易错点是一辆车后退时要注意另一辆车的行进速度，在后退的这段路上，两辆车的速度是一样的，都是后退的那辆车的速度。线段图的直观形象可以让学生扫清解题过程中的易错点：学习能力一般的学生借助线段图可以得到两种方案，最后比较得出结论；思维能力较强的学生借助线段图可以直接判断出由小汽车后退以让大卡车先通过的方案用时最少。线段图将繁杂的文字叙述转化成形象的数学图形，把隐藏的数量关系显现出来。学生在画线段图的过程中可以进一步厘清题干数量关系，从而找到解题思路，得出正确的答案。

三、导图助思维，表达思考过程

数学课堂上，教师要创造机会让学生独立思考、交流讨论、大胆表达。而不论在思考还是在表达思考的过程中，学生都可以通过思维导图的方式，对各知识点之间的联系进行推理、解构，再整体联系起来，从而找到解决问题的思路，得出答案。

例如，教学人教版数学六年级（下册）复习课“平面图形的整理与复习”时，课上，教师让学生对单元知识进行梳理。教师发现学生思维水平存在明显的差异性：列举式（文字+图形）、推导式（文字+图形）、网络式（图形+文字符号）。具体如图3所示。

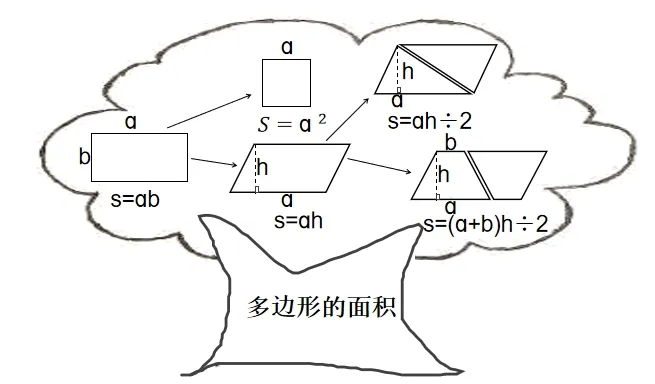
图3

三种表现形式都离不开文字和图形，可见图式在数学表达中占据重要地位。绘制图3的学生思维水平已达到较高阶段，他回顾学过的图形面积公式，明晰这些图形面积公式是如何推导出来的，架构起这些知识间的联系。教师利用这些思维图，可以进一步引导学生借助转化的思想将这些图形的面积计算公式进行变通，由此让学生深刻体会到可以从任意一个多边形的面积计算公式推导出其他多边形的面积计算公式。

结 语

综上所述，在小学数学教学中，教师如能巧妙利用“图式”直观，运用数形结合的教学方法，帮助学生深刻理解数学概念的本质，厘清问题中的数量关系，清晰表达解题思路，就能降低数理的学习与表达难度，使学生能够更好地掌握数学知识。在此过程中，学生的高阶思维能力及学习质量也将会有质的飞跃。