一种新的配对等级资料统计推断方法*

南方医科大学公共卫生学院生物统计学系(510515) 吴研鹏 周立志 陈平雁

【提 要】 目的 针对配对等级资料，提出一种新的统计推断方法，并通过统计模拟，与经典的非参数检验方法进行比较。方法 基于配对等级资料差值的离散性和多项分布特征，构造一种新的统计量AOC(average order change)，即加权平均等级差，以及相应检验方法。应用Monte Carlo技术，比较AOC检验与Wilcoxon符号秩检验(Wilcoxon法)、Pratt法的统计性能。结果 在样本量小于30时，三种方法的I类错误率偏于保守，其中Wilcoxon法偏离设定水平较大；在样本量大于或等于30时，I类错误率均接近设定水平，以AOC检验更接近设定水平。当样本量小于20时，检验效能以Wilcoxon法较低，AOC检验和Pratt法相当；在样本量大于或等于20时，三种方法的检验效能非常相近。结论 在统计性能方面，AOC检验与Pratt检验表现相当或略优。在统计量意义上，AOC更能直观表达等级变动情况。

配对等级资料在医学研究中颇为常见，其特点之一是可能会有较大比例的零差值(zero differences)和相同秩(ties)[1-2]。对于相同秩，已有对应的校正方法[3]。对于零差值，大部分非参检验包括最常用的Wilcoxon符号秩检验，是删除零差值的数据后进行分析。这种处理的缺陷是损失信息，特别是零差值的比例较大时，会使统计推断产生偏倚[4-5]。对此问题，Pratt[5]提出的处理方法是，先对包含零差值的所有差值进行排秩，然后删去零差值观测单位，再运用Wilcoxon法对剩下的秩次进行检验。目前，有关Pratt法的模拟研究较少，其统计性能如何尚待回答[6]。因此，本研究基于不损失信息和更具可解释性的前提，提出一种新的比较配对等级资料的统计方法。

原理和方法

1.统计模型

假设某项临床试验一组病例的样本量为N，疗效评价指标为疾病严重程度，分为K个等级，治疗前后疾病严重程度等级的变化即等级差用D(D1，D2，…，DN)表示。显然，Di的取值范围为-(K-1)～(K-1)，所有可能的取值个数为2K-1，每种可能取值对应的频数为Fi，对应频率为fi=Fi/N，概率为πi。具体构成见表1。

表1 配对等级数据等级差的分布

这里，我们根据加权平均等级差的思想定义一个统计量AOC(average order change)，即

(1)

这里差值Di在配对等级数据中可看作两组前后的等级变动级数，级数为正，表示向上变动级数，级数为负，表示向下变动级数，为0表示级数不变。fi表示等级变动级数Di对应的频率。由公式(1)定义的AOC则表示总的等级变动级数的均值，当AOC取0时，配对两组等级前后变动的均值为0，表示治疗前后无差异。

AOC的方差估计为

(2)

由于fi服从对应概率为πi的多项分布[7]，进一步得出

(3)

在AOC=0的原假设下，可以构建如下检验统计量z，

(4)

2.模拟方法

基于双变量正态分布产生配对等级数据[8]。在双变量正态分布中，参数μ1和μ2分别对应配对两组的均值，σ1和σ2对应各自的标准差，协方差大小由相关系数ρ决定，即ρσ1σ2。在以上参数组合下，运用Monte Carlo技术模拟生成特定的双变量正态分布数据，然后根据结局等级数，对双正态分布数据进行等面积划分。本研究只考虑临床常见的三等级，四等级和五等级分类的配对资料比较，即对生成的双变量正态数据进行三等分，四等分，五等分。具体模拟参数设置如下：

(1)双变量正态分布设置：配对两组无差异情况下，则μ1=μ2=0；存在差异情况，设μ1=0，μ2=0.3，0.5，0.8，1.0，1.3，1.5，1，8，2.0；

(2)双变量正态相关系数：ρ=0.2，0.4，0.7；

(3)等级数：K=3，4，5；

(4)样本量N=10，15，20，25，30，35，40，45，50，55，60，65，70，75，80，85，90，95，100；

检验水准设置为双侧0.05，每种参数组合模拟次数为10000次，采用R 3.6.3编程实现。

结 果

不同等级数和相关系数组合下，AOC检验、Wilcoxon法和Pratt法的I类错误率随样本量变化的模拟结果见图1。图1中每个子图中横轴表示样本量，纵轴表示I类错误率，按等级数K和相关系数ρ大小分别以横向和纵向排列，并给出对应组合下的零差值的比例大小(%)。显然，高相关系数低等级水平下，零差值比例更高。可以看出，当样本量小于30时，三种方法的I类错误率均偏离设定水平0.05较大，且绝大多数是小于设定水平；当样本量大于或等于30时，三种方法的I类错误率均接近设定水平，以AOC检验更接近设定水平，而且，样本量的增大对I类错误率没有趋势性影响。

图1 不同等级水平和相关系数下的I类错误率比较

图2展示不同等级数和相关系数组合下，三种方法检验效能的比较。每个子图中，横轴为样本量，纵轴表示检验效能，按等级数K和相关系数ρ大小分别以横向和纵向排列，并给出对应组合下的零差值的比例大小(%)。可见，当样本量小于20时，检验效能以Wilcoxon法较低，AOC检验和Pratt法相当；当样本量大于或等于20时，三种方法的检验效能非常相近。

图2 不同等级水平和相关系数下的检验效能比较

实例：瑞典一项研究招募了92名患者，使用Rand-36健康生活质量表，记录该组病人在参与心脏康复计划之前和3个月后的健康质量评价[9]。Rand-36中感受评价指标分为5个等级，分别赋值为：1(很差)，2(较差)，3(一般)，4(较好)，5(很好)。该组病人在基线值和治疗3个月后的自我评价健康情况见表2。

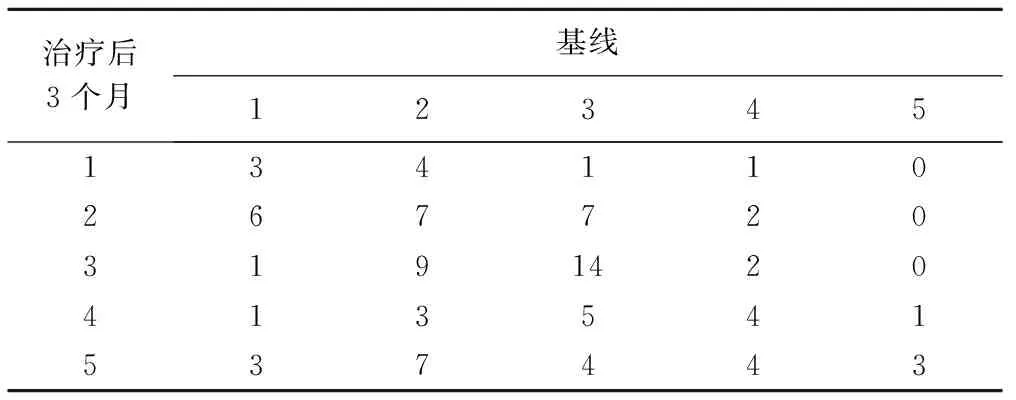
表2 心脏康复病人在基线和随访的自我健康评价

对表2资料采用AOC检验，定义等级差为治疗后-基线(治疗前)，得统计量AOC为0.577，95%置信区间为0.266～0.886，P值为0.00026。采用Wilcoxon法和Pratt法的P值分别为0.00031和0.00045。在检验水准0.05下，三种检验均显示差异显著，但AOC可以直观表示治疗后患者的健康水平平均改善了0.577个等级。

讨 论

本研究根据加权平均的思想，提出了AOC统计量，其优点是直观和良好的解释性，而且充分利用了零差值的信息。

在统计性能的I、II类错误方面，模拟研究提示，AOC检验与Wilcoxon法、Pratt法相当或略优，特别是在零差值比例很大或样本量较小的情形。

本研究存在一定的局限性。首先在模拟方面，目前只是在方差齐性和双变量正态分布的假设下模拟数据。然而在实践中，常会出现异方差和非正态分布情况，该种情况下的统计性能表现需要进一步验证。其次，新方法的提出是基于渐进正态分布下的推导，小样本的精确检验还需进一步研究。

综上所述，本研究建立的AOC检验具有良好的解释性和较为可靠的统计性能，可应用于配对等级资料的检验。