地锚式独斜塔混凝土斜拉桥抗震性能

王晓佳，张瀚钊，张祖军

（1.保利长大工程有限公司，广东 广州 510000；2.长沙理工大学 土木工程学院，湖南 长沙 410114；）

随着国内经济建设的大力发展，新建桥梁的跨径不断增大，桥梁结构逐渐多样化，现已不单单追求桥梁的通行功能，桥梁的美观也成追求之一。斜拉桥的承载能力强，跨越能力大，外形美观，能很好地与城市和山区环境融为一体，深受桥梁设计与建设者的喜爱，当前已成为跨越山川峡谷、江河湖泊且极具竞争力的桥型之一[1-3]。但对斜拉桥的抗震性能也提出了更高要求，国内外学者对其抗震性能开展了大量研究。阮怀圣等人[4]对5座公铁两用钢桁梁斜拉桥的动力特性进行了统计分析，并采用有限元软件分析了不同结构抗震约束体系的抗震响应特征。沈星等人[5]研究了大跨度斜拉桥边墩横向抗震体系，提出了边跨主梁横向基本周期的简化计算公式。邱景雷等人[6]采用有限元手段对一座高塔大跨径斜拉桥的地震响应进行了研究，并对比了设置阻尼器后斜拉桥的减震效果。全伟等人[7]采用Midas Civil 建立了某高铁矮塔斜拉桥模型，分析了其在不同减隔震装置下的减震机理和效果。许莉等人[8]以一座主跨为680 m的对称大跨径双塔斜拉桥为背景，设计了1:40 缩尺比的半桥模型，并开展振动台模型试验，研究了其纵向地震响应。周玲玲[9]采用有限元软件对某地锚式独斜塔斜拉桥开展了不同力学荷载下的受力性能研究，但主要偏向于静力分析。宗周红等人[10]采用LS-DYNA 有限元软件建立了大跨度斜拉桥模型，开展了强震作用下大跨度斜拉桥增设阻尼器和辅助墩前、后的抗震性能。禹建兵等人[11]以国内某混凝土斜拉桥为背景，分析了采用不同结构体系的斜拉桥地震响应特征。Li 等人[12-13]开展了独塔和多塔斜拉桥的振动台试验，研究了其抗震性能。但针对斜拉桥的抗震性能研究主要以传统类型的斜拉桥为主，而针对单跨地锚式独斜塔混凝土斜拉桥的抗震性能研究较为少见。因此，作者拟采用Midas Civil 2019 建立国内某单跨地锚式独斜塔混凝土斜拉桥三维有限元模型，对其抗震性能进行研究，分析在不同地震动方向和阻尼比影响下的地震时程响应规律，可为工程抗震设计与计算提供参考。

1 工程背景

国内某斜拉桥跨径为170 m 的单跨地锚式独斜塔混凝土斜拉桥。主梁断面采用Π 型，宽度为29 m，高度为2.5 m。斜拉索采用扇形布置，主梁拉索间距为8 m，背索间距为1.65 m，主塔上的拉索间距为1.5～3.0 m 之间变化。主塔采用“人”形桥塔，由上塔柱、下塔柱、横梁等组成，斜塔与水平地面的倾角为71.57°。承台底部共10 根桩基，桩径4.0 m，顺桥向两排，一排为竖直桩，另一排为斜桩，承台采用长47 m，宽13.5 m，高5 m的整体式结构[9]，斜拉桥总体布置如图1所示。

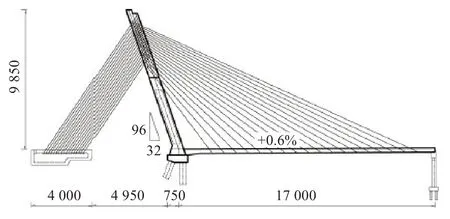
图1 地锚式斜拉桥总体布置（单位：cm）Fig.1 General layout of ground-anchored cable-stayed bridge（unit:cm）

2 有限元模型的建立

采用Midas Civil 2019 有限元软件建立了全桥三维有限元模型。全桥共划分292 个单元，377 个节点。主塔、主梁、承台和桩基础均采用杆系梁单元模拟，斜拉索采用桁架单元模拟。桥塔和主梁分别与拉索通过刚性连接，模型中未考虑地锚箱影响，直接在背索底部采用固结。模型中也未考虑辅助墩的影响，仅在主梁末端释放其纵向平动和竖向转动。主梁与主塔之间采用刚性连接，主梁、承台及其下桩基三者均采用刚性连接。通过一系列的土弹簧模拟桩-土相互作用，弹簧刚度采用m 法计算。斜拉桥空间视图和横向视图如图2所示。

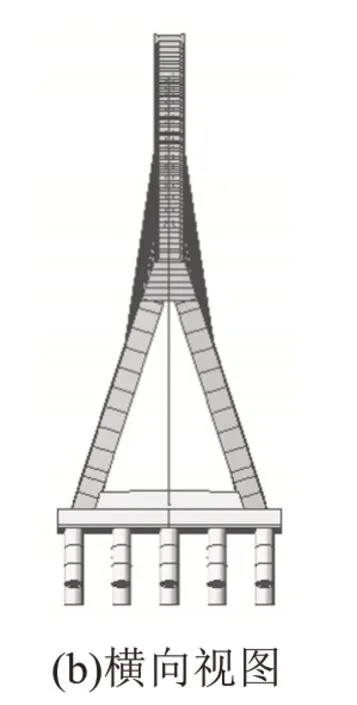
图2 斜拉桥有限元模型Fig.2 Finite element model of cable-stayed bridge

3 动力特性

采用多重Ritz向量法计算单跨地锚式独斜塔混凝土斜拉桥的动力特性，分析了前50阶自振模态，各方向振型参与质量均达到了90%以上，可满足抗震规范要求。斜拉桥前10 阶的自振频率及对应的自振模态见表1，第1 阶和第2 阶自振模态的空间视图和侧向视图如图3～4所示。

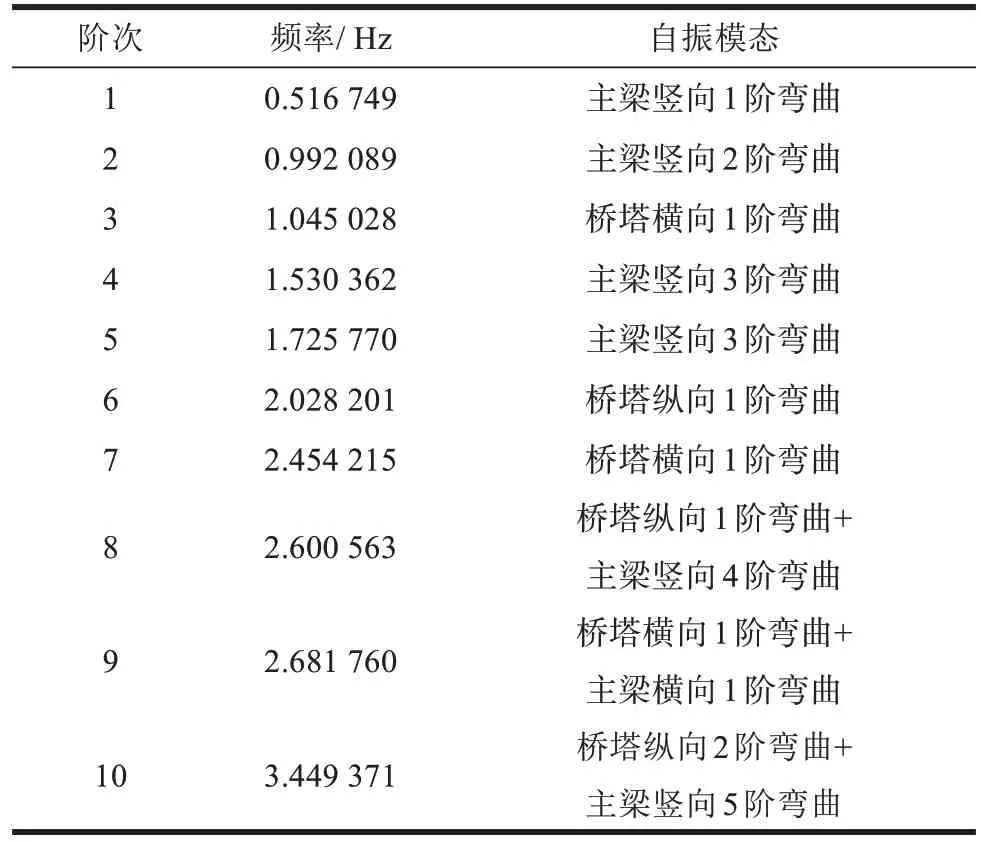
表1 斜拉桥前10阶的自振频率及其对应的自振模态Table 1 The natural vibration frequencies of the first 10 orders and vibration modes of cable-stayed bridge

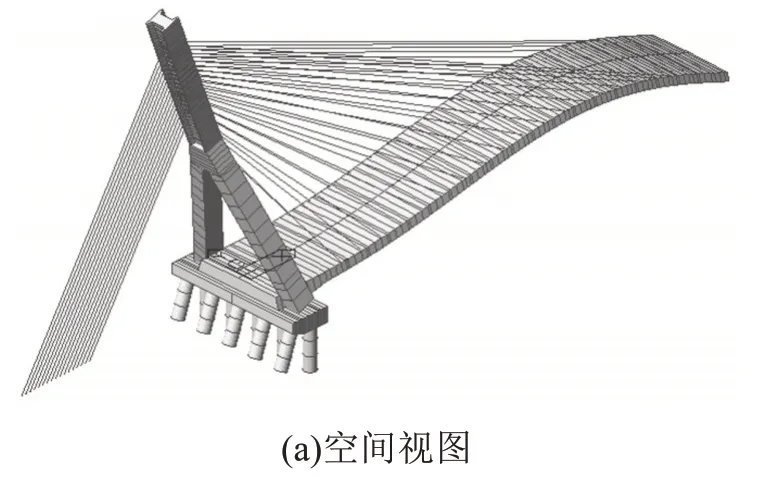
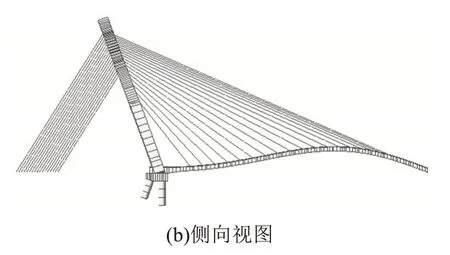
图3 斜拉桥第1阶自振模态Fig.3 The first natural vibration mode of cable-stayed bridge

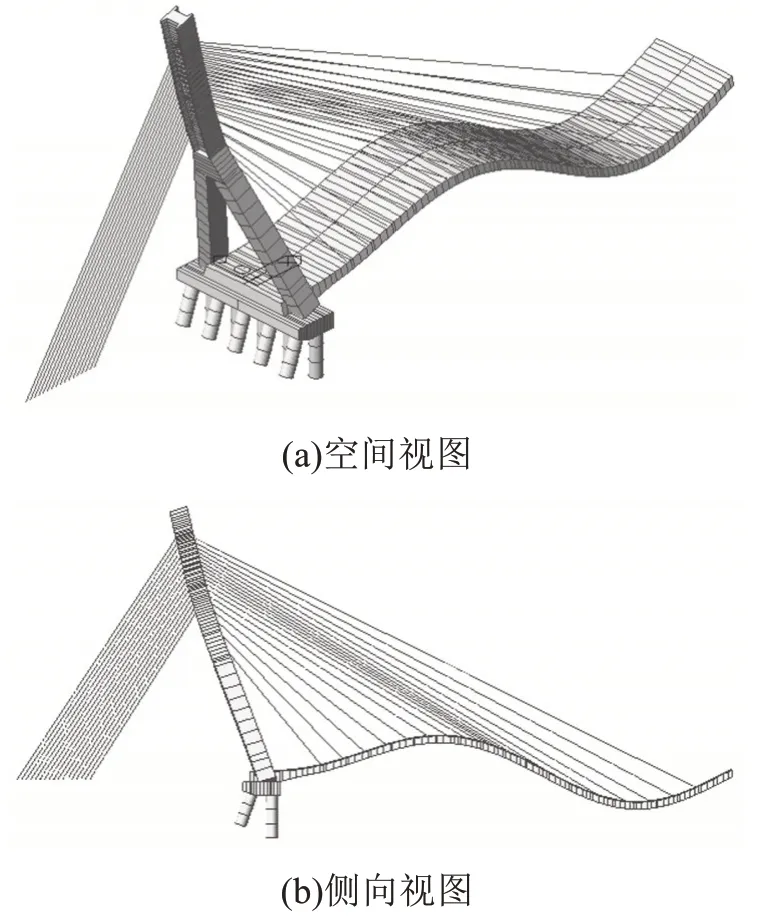
图4 斜拉桥第2阶自振模态Fig.4 The second natural vibration mode of cable-stayed bridge

由表1和图3～4可知，斜拉桥第1阶的自振周期最大，表现为主梁竖向1阶弯曲，为斜拉桥的主振模态。第2 阶出现了主梁竖向2 阶弯曲，应重点考虑主梁振动引起的斜拉索受拉，避免斜拉索的断裂。直至第3阶才表现为桥塔振动，表明桥塔的整体刚度较大。前10 阶振型的自振频率在0.516 749～3.449 371 Hz 之间，频率相差最大接近3 Hz，分布较为紧密，表明斜拉桥整体结构相对较柔。

4 地震响应参数敏感性分析

4.1 地震波的选取

斜拉桥的抗震设防类别为B类，二类场地，特征周期0.4 s，设防烈度7 度，地震加速度峰值为0.15g（g为重力加速度），阻尼比0.05。本试验选用加速度峰值为0.179 3g的Taft 波作为地震输入波，同时考虑水平向和竖向的地震输入波。其中，水平向输入波采用0.179 3g的Taft波，而竖向输入波取水平向输入波的0.65 倍，即最大加速度峰值为0.116 545g。地震波持续时间通常取5～10 倍的基本周期，本试验取地震波前20 s进行地震响应分析。水平向Taft 地震波如图5 所示，调整后的竖向Taft地震波如图6所示。

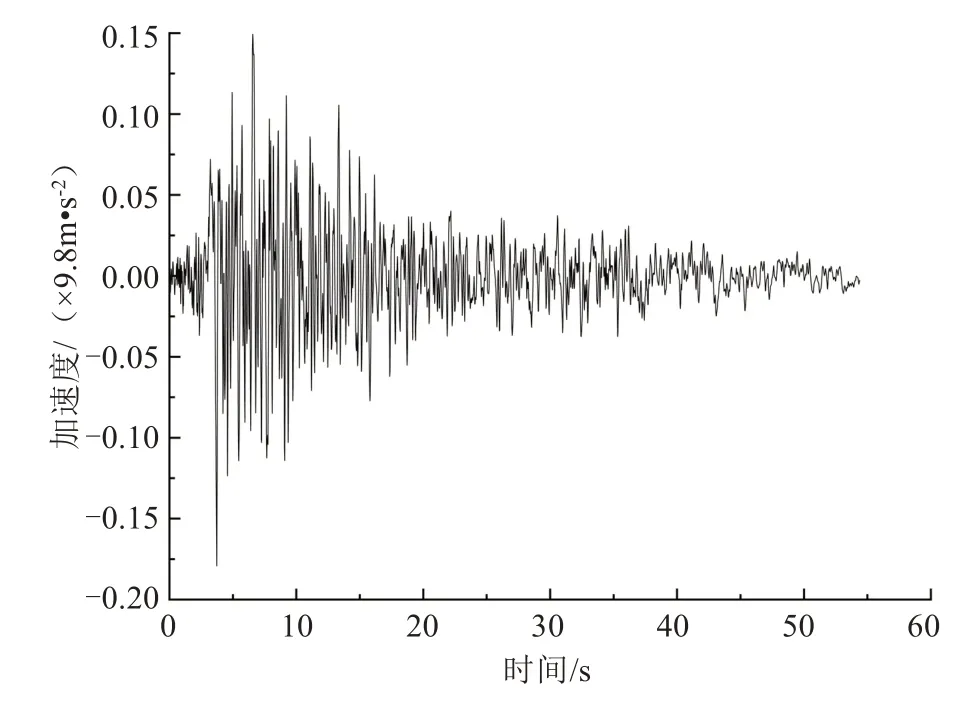
图5 水平向Taft地震波Fig.5 The Taft seismic wave of horizontal

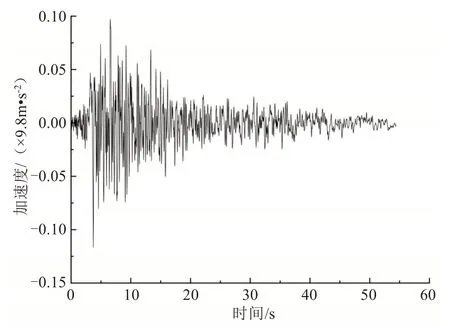
图6 调整后的竖向Taft地震波Fig.6 The Taft seismic wave of vertical after adjusted

4.2 地震动方向的影响

采用的地震输入波阻尼比为0.05，分别沿着纵桥向、横桥向、竖桥向进行激励，计算主梁跨中、主梁端部、桥塔底部的最大弯矩和位移。输入波3个方向对斜拉桥各位置的最大弯矩和位移见表2～3。

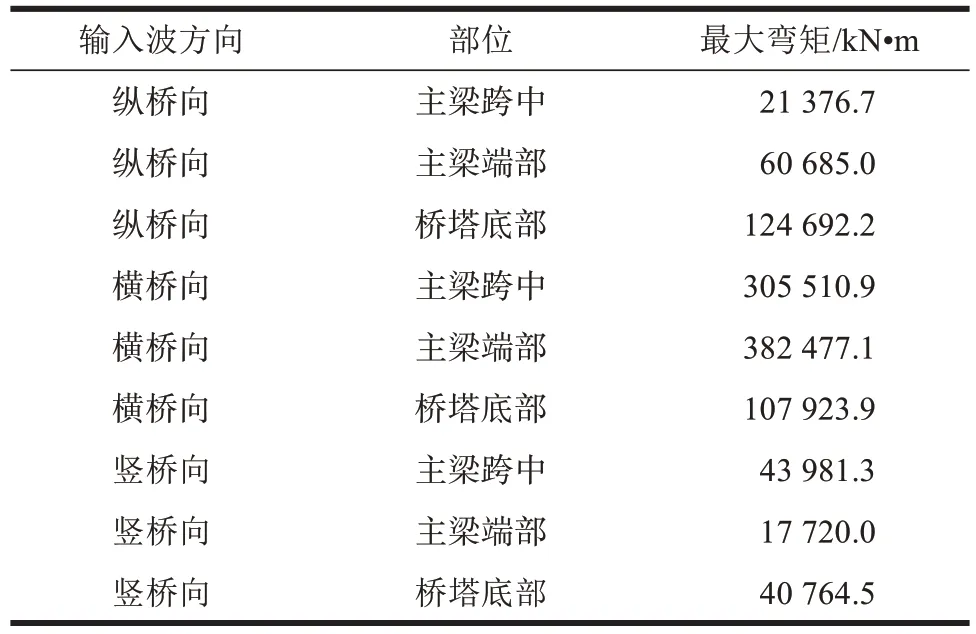
表2 输入波3个方向的斜拉桥各部位的最大地震弯矩Table 2 Maximum seismic bending moment of cable-stayed bridges by three-direction input waves

表3 输入波3个方向的斜拉桥各部位的最大地震位移Table 3 Maximum seismic displacement of cable-stayed bridges caused by the three-direction input waves

由表2可知，在纵桥向输入波激励下，桥塔底部会出现很大弯矩，混凝土受弯最严重，容易出现混凝土开裂，因而在抗震设计时应重点考虑桥塔底部的受弯验算。在横桥向输入波激励下，主梁端部（即承台处主梁部位）会出现很大负弯矩值，主梁跨中也出现了极大正弯矩值，主要是该处主梁、承台和桥塔两两固结所致，设计中应考虑横桥向地震荷载对主梁端部上缘混凝土受拉问题。竖桥向输入波对桥塔和主梁弯矩的影响最小。

由表3可知，竖桥向地震荷载对主梁跨中变形的影响最大，分别是纵桥向的2.36 倍和横桥向的4.53倍，重点开展竖桥向地震荷载下的主梁变形验算。而对于桥塔变形，在横桥向地震荷载下最大，分别是纵桥向的2.16 倍和竖桥向的4.09 倍。表明：横桥向地震荷载对桥塔的稳定性影响最大，过大偏位对主塔受力极为不利，在抗震验算时应尤其关注横桥向的地震荷载，并采取有效抗震措施控制桥塔侧偏。

4.3 阻尼比的影响

混凝土的阻尼比一般为0.05，设置合理的阻尼比对结构的抗震设计极为重要。本试验取阻尼比为0.02 和0.05，分别研究阻尼比对斜拉桥主梁跨中、主梁端部和桥塔底部的最大弯矩和位移地震响应。

同时考虑3个方向的地震输入波，采用的组合工况为：纵桥向Ex+横桥向Ey+竖桥向Ez，组合工况下不同阻尼比斜拉桥各部位的最大地震弯矩和位移值见表4～5。组合工况下主梁跨中最大弯矩、端部最大弯矩和跨中最大位移地震时程响应如图7～9 所示。组合工况下塔底和塔顶最大弯矩和位移的地震时程响应如图10～11所示。

表4 不同阻尼比下斜拉桥各部位最大地震弯矩Table 4 Maximum seismic bending moment of cable-stayed bridges under different damping ratios

表5 不同阻尼比下斜拉桥各部位最大地震位移Table 5 Maximum seismic displacements of cable-stayed bridges under different damping ratios

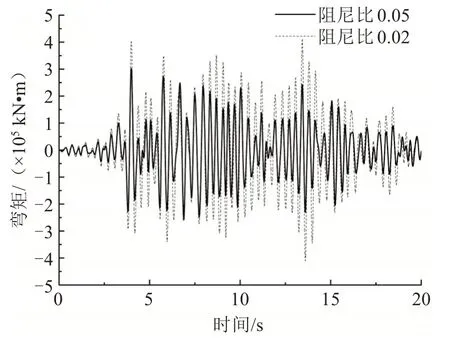
图7 主梁跨中的最大弯矩地震响应Fig.7 Seismic responses of maximum bending moment of girder at the mid-span

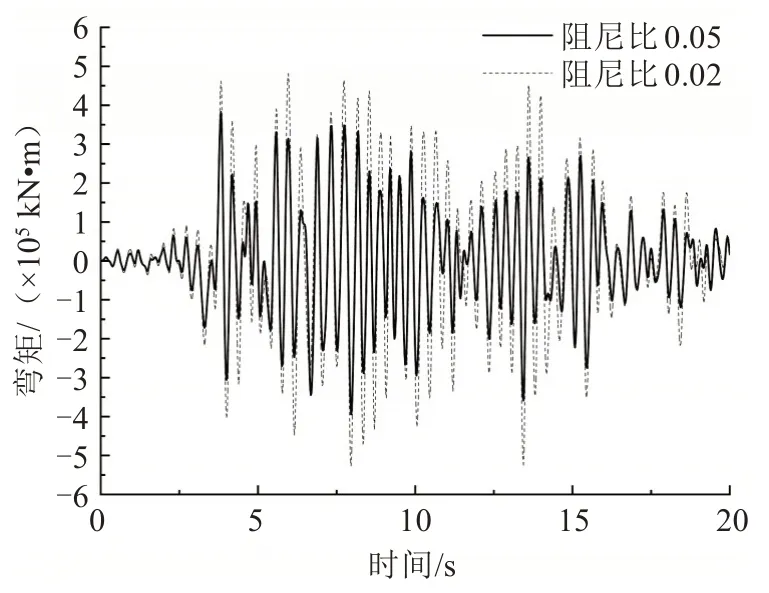
图8 主梁端部的最大弯矩地震响应Fig.8 Seismic responses of maximum bending moment of girder at the end

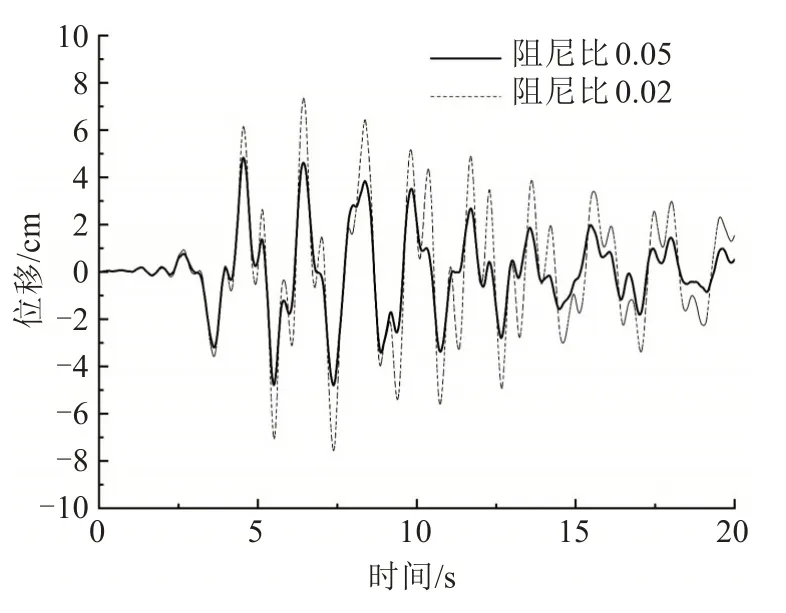
图9 主梁跨中的最大位移地震响应Fig.9 Seismic responses of maximum displacement of girder at the mid-span

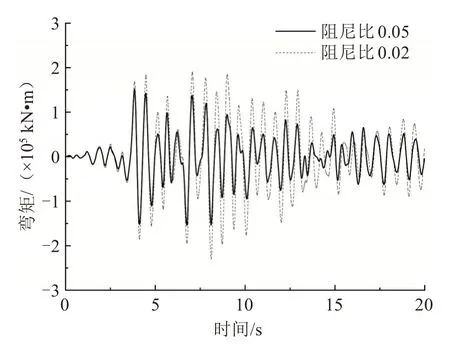
图10 塔底最大弯矩地震响应Fig.10 Seismic responses of maximum bending moment of tower at the bottom

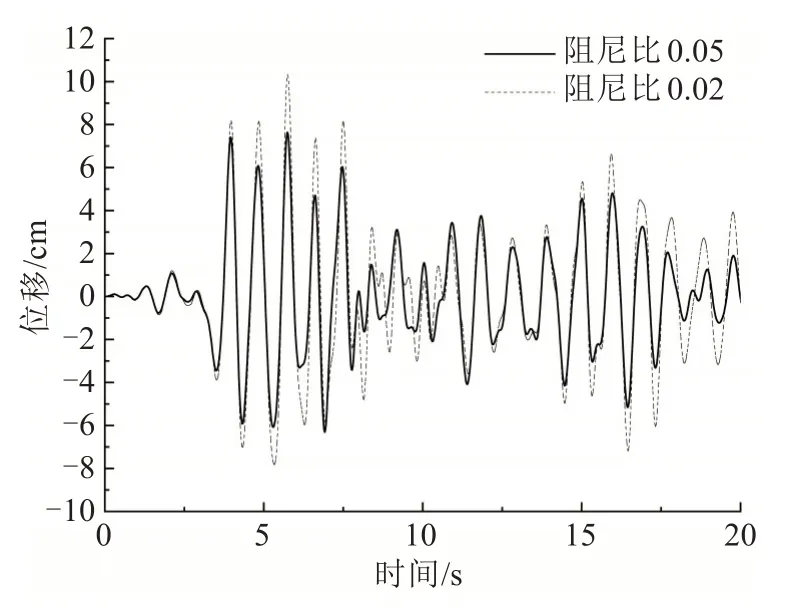
图11 塔顶最大位移地震响应Fig.11 Seismic responses of maximum displacement of tower at the top

从图7～11 中可以看出，阻尼比减小会使得斜拉桥主梁、桥塔的最大弯矩和位移地震时程响应明显提高。由表4可知，随着阻尼比降低，主梁跨中的最大弯矩值提高了36.1%，主梁端部的最大弯矩值提高了33.5%，桥塔底部的最大弯矩值提高了49.1%。表明：阻尼比降低使得桥塔底部的弯矩地震响应增大最明显。由表5可知，随着阻尼比的降低，主梁跨中的最大位移值提高了56.3%，主塔顶部的最大偏位值提高了35.1%。因此，阻尼比的降低对主塔弯矩和主梁位移的地震响应影响最大。在斜拉桥抗震设计时，合理设计结构的阻尼比，可以有效地改善其地震响应。

5 结论

采用Midas Civil 2019 建立了地锚式独塔混凝土斜拉桥有限元模型，研究了纵向、横向、竖向地震波输入和阻尼比对主梁和桥塔的弯矩和位移地震时程响应的影响规律，得出结论为：

1）斜拉桥的整体结构相对较柔，主振模态为主梁竖弯，容易引起斜拉索的受拉断裂问题。

2）在纵桥向地震激励下，塔底会出现很大弯矩，混凝土受弯最严重，容易引起开裂，在设计中应考虑塔底受弯验算。

3）在横桥向地震激励下，应重点关注主梁端部上缘的混凝土受拉问题。横桥向地震荷载对塔顶变形影响最大，容易引起桥塔失稳，应采取有效抗震措施减小横向地震荷载的影响。

4）竖桥向地震荷载对主梁跨中的变形影响最大，而对桥塔和主梁弯矩的影响最小。

5）阻尼比降低会显著增大主梁和桥塔的弯矩和位移地震响应，且对塔底弯矩和主梁跨中竖向挠度的地震响应影响最大。在斜拉桥抗震设计时，合理设计结构的阻尼比，可以有效地改善其地震响应。