基于静载试验的PPC斜拉桥有限元模型修正分析
陈羽中,张家滨,颜东煌
(长沙理工大学 土木工程学院,湖南 长沙 410114)
有限元模型修正理论已有五十多年的发展,许多学者对有限元模型修正技术提出了改进和创新,提高了有限元模型的可靠度和精确性,能更好反映结构真实情况和状态,常运用于桥梁工程的实际应用中[1-2]。斜拉桥通常依据设计参数建立初始有限元模型。由于有限元模型中理想化的边界条件与实际工程结构的真实边界条件存在差异,导致有限元模型不能反映实际结构的真实状态。因此,需要采用有限元模型修正技术对初始有限元模型进行修正,将误差控制在工程允许范围内。基于静力试验有限元模型修正,通常使用静力试验中测量出的挠度值或静态应变与仿真结果的差值作为目标函数的设定依据。相对于动力试验中测量出的固有振型等数据,静载试验的数据更准确、更可靠[3-4]。夏品奇等人[5]以新加坡的Safti桥为研究背景,建立了有限元模型,并进行了修正,修正中考虑斜拉索垂度效应,基于灵敏度修正后得到Safti桥可靠的有限元模型。宗周红等人[6]通过对比其他学者的修正方法,提出了联合模态柔度和静力位移的有限元模型修正方法。李义强等人[7]利用最小二乘法构建了目标函数,以混凝土梁为研究对象,提出了基于参数识别的静力模型修正方法。谢海龙[8]对一座先简支后连续预应力混凝土箱梁桥进行荷载试验,搜寻目标函数最优解,达到有限元模型修正目的,修正过程中舍弃了GN法,引入了阻尼因子LM 法。刘天怡等人[9]利用模态频率、模态振型和模态柔度组合指标作为神经网络修正的输入参数,并以实例进行验证,比较不同输入参数的模型修正精度。模态柔度作为一种损伤识别新指标,被学者们广泛运用在实际工程中[10-12]。杨秋伟等人[13]研究发现利用广义柔度矩阵灵敏度进行损伤识别时,并非阶次越高识别结果越准确,因而通常采用一次或二次广义柔度矩阵。本研究拟利用振型、固有频率及模态柔度关于索及支座刚度之间的灵敏度系数,推导基于柔度的灵敏度矩阵,基于静载试验的有限元模型修正方法对模型进行修正,并以多种实际工况验证修正后的有限元模型仿真实际结构。
1 有限元模型修正方法
1.1 模态柔度矩阵
多自由度体系振动特征方程通常可表示为:

式中:K为结构的总刚矩阵;M为结构的总质量矩阵;ωr为结构在第r阶的圆频率;φr为结构在第r阶的特征振型,r=1,2,···,n。
对振型质量归一化,且式(1)满足正交条件,即:

式中:Φ= (φ1,φ2,···,φn)。
柔度矩阵D通常是刚度矩阵K的广义逆矩阵,文献[14]定义了柔度矩阵D和刚度矩阵K。运用模态参数的表达式为:

式中:φr是进行归一化处理后的第r阶振型向量。
对比式(3)和式(4)可知,柔度矩阵与频率的平方成反比,随着模态阶数越高,模态对柔度的影响越小。实际工程中,有限元对高阶模态仿真结果较差,因此,利用高阶模态对柔度矩阵影响微弱的特性,在计算过程中只取有限元模型中低阶模态参数构建柔度矩阵D进行模型校验。
假设真实柔度矩阵为Da,初始有限元模型模态参数构建的柔度矩阵为Do。通过试验得出模型挠度为Ua,假设试验值为真实值,由有限元模型计算响应挠度为Uo。根据柔度矩阵与位移的关系,可得:

式中:f为荷载向量;Ua、Uo分别为位移向量。
将式(5)、(6)相减,即为试验结果与仿真计算结果间的误差。

对应的柔度矩阵间差值ΔD为:

通过对柔度矩阵与待修正参数间的灵敏度分析,得到挠度差值与待修正参数的关系表达式,实现有限元模型修正。
1.2 灵敏度分析
基于静载试验的有限元模型修正,对结构待修正参数进行灵敏度分析,柔度矩阵的灵敏度为有限元模型修正提供了快速搜索的方向。通过模态柔度法,推导模型关于某一单元参数Kj的灵敏度,Kj通常为结构边界支撑的刚度、模型的设计参数等。
求解结构体系的固有频率就是求解多自由度振动特征方程的特征解λ,λ=ω2,则为结构在第r阶的特征值,r=1,2,···,n,将其带入式(3),即:

将式(9)对单元参数Kj求偏导,得:
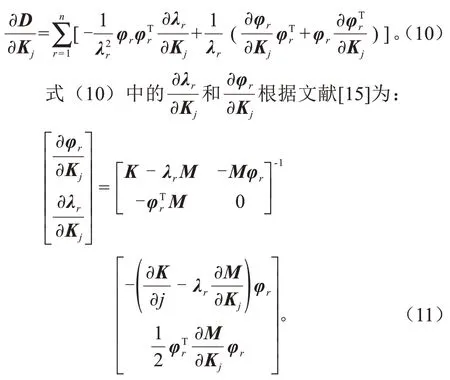
本研究修正目标为斜拉索的刚度和边界支撑刚度,质量矩阵与斜拉索和边界支承刚度无关,所以式(11)中,整理式(11)得:
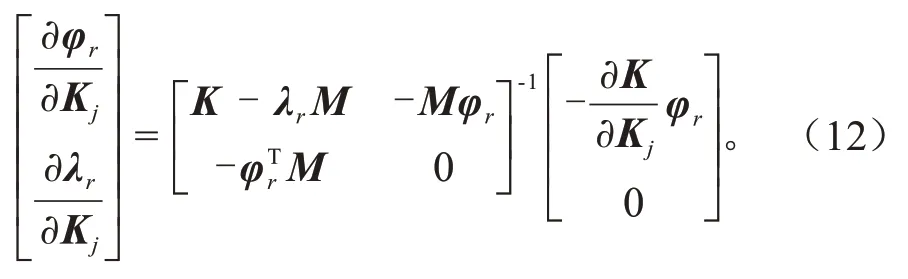
根据差分法,柔度矩阵对单元参数Kj的导数可改写为:
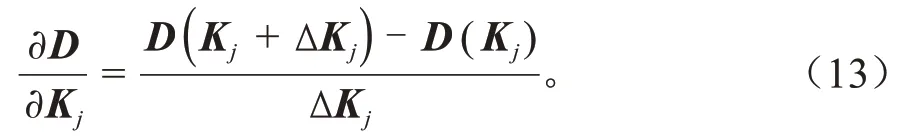
根据式(5)、(6),挠度U对单元参数Kj的灵敏度分析,得到:

在式(15)中,力向量f与Kj无关,因此,整理得到单元参数K与挠度U的关系j式为:

式(17)中ΔU与ΔKj的具体表达式为:

式(20)给出挠度残差与单元参数修正值的关系表达式。每次修正后,迭代计算理论挠度向量,并再次计算新的挠度残差,循环迭代。
修正有限元模型,挠度残差ΔU需无限趋近于0,则代表有限元模型与真实结构相一致,联立式(5)~(8),整理可得:

当ΔU= 0 时,表明:理论挠度值等于试验挠度值,且理论柔度矩阵等于真实柔度矩阵。
为实现有限元模型能仿真实际结构,使理论挠度值与试验挠度值差别最小。ΔU为一列向量,实质上是模型n个节点上的残差位移,可表示为:
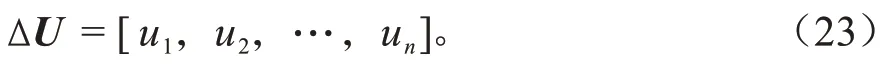
利用最小二范数原理,构造有限元模型修正的优化目标函数:

挠度修正实质上是对柔度矩阵修正,挠度残差最小化实质上是模态柔度残差最小化。挠度残差在单元参数ΔKj附近进行摄动,对其过程进行一阶泰勒级数线性展开,可得:

式(25)中,ΔUk为第k次迭代时的位移残差;为迭代时灵敏度矩阵,每次迭代时都会发生变化;ΔKj为迭代时的单元参数增量。
联立式(24)、(25),可得到每次迭代入式(24),即:
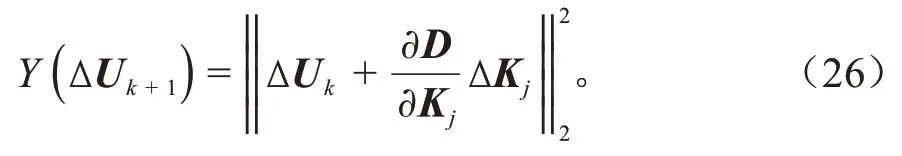
2 模型与试验布置
本试验以广州南二环李家沙大桥为工程背景,采用(38+72+220+72+38)m 的桥跨布置,边中跨比为0.5,桥梁横向宽度50 m。该桥设置等效的节段缩尺模型,砼强度等级为C50,混凝土弹性模量为 3.5×104 MPa,混凝土密度为 2.55×103 kg·m3,泊松比为 0.3,K1 刚度为 3.39×103 kN/m,K2 刚度为6.71×103 kN/m,斜拉索弹性模量为1.95×105 MPa,斜拉索截面面积为1.39×10-4m2,10#索的长度为12.58 m,11#索的长度为13.49 m,12#索的长度为14.42 m,13#索的长度为15.34 m,14#索的长度为16.28 m。模型上张拉的5 根斜拉索编号从左至右分别为10#~14#。节段模型试验现场如图1 所示。模型主梁两端支撑在弹簧上为弹性支撑,左侧弹簧支撑为K1,右侧弹簧支撑为K2。梁的左端设置轴承与止推装置,并借助钢横截梁和混凝土支墩直接顶在左侧剪力墙上,以限制纵桥向的位移。主梁两侧焊接2 个H 型钢,以限制横向位移。模型具体情况参考文献[16],截面示意图如图2 所示,模型结构示意图如图3所示。

图1 试验模型的布置Fig.1 The layout of the test model
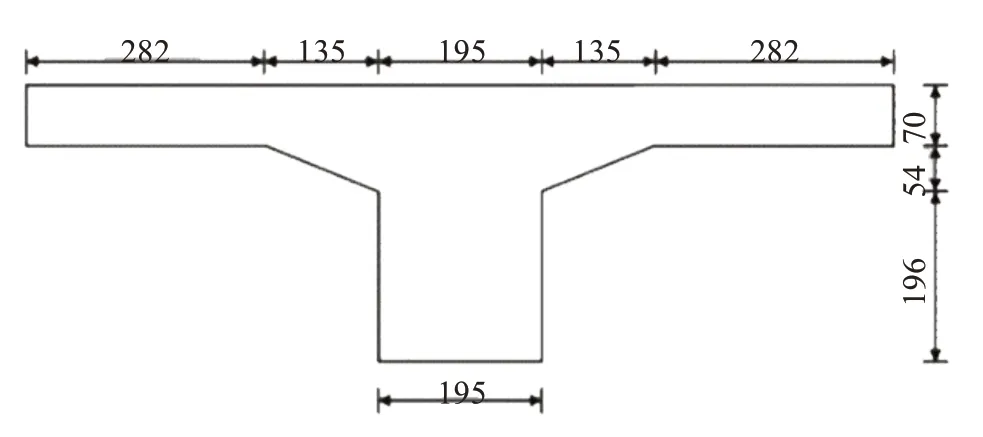
图2 模型横截面示意(单位:mm)Fig.2 The cross-section(unit:mm)

图3 模型结构示意Fig.3 The model structure diagram
2.1 加载方案
本试验以挠度残差作为目标函数,对初始有限元模型进行修正。因此,在部分预应力混凝土(partially prestressed concret, 简称为PPC)斜拉桥缩尺模型上进行静力荷载试验,收集记录各测点的挠度值。在模型跨中270 m 处,以2 种集中荷载方式进行加载:
工况一,选取16 kN 集中荷载作用;工况二,选取12 kN集中荷载作用。
2.2 挠度测点布置及测试结果
试验中,以梁左端支座为原点,在0、1.35、2.70、4.40、6.00 m 处,分别布置5 个动态位移数据采集点,其余8 个静态位移计按照位置均匀布置,位移计精度为0.01 mm,布置情况如图4所示。以2种工况的数据为实例进行修正,试验中实测挠度值见表1。挠度方向向下为正值。

图4 位移计布置情况Fig.4 The layout of the displacement gauge

表1 各个测点挠度值变化Table 1 The change of deflection of measuring points
3 算例
3.1 初始有限元模型
根据模型的设计参数和竣工图纸,采用MATLAB 软件,按照结构的实际尺寸建立PPC 斜拉桥有限元模型。模型中的梁段部分,单元刚度矩阵采用平面弯曲梁单元,单元质量矩阵采用协调质量矩阵。挂篮体系中,单元质量矩阵采用集中质量矩阵。斜拉索由轴向杆单元构建。模型中,梁段部分、支撑边界和斜拉索联接处共用节点实现共同协调受力。
斜拉索的设计参数见表2,弹性模量E=1.95×105MPa,横截面积A=1.39×10-4m2,根据斜拉索的刚度计算公式K=EA/L,可计算出斜拉索的初始刚度。5根斜拉索施加在梁单元上的初始刚度见表2。

表2 斜拉索设计参数Table 2 The design parameters of stay cables
试验模型的设计方案中,左侧的边界情况较为复杂,除了竖向弹簧支撑K1,在梁的左端还设置轴承与止推装置;右侧的边界条件主要是竖向弹簧支撑K2;梁的左右两侧焊接了H 型钢,限制梁的横向位移,如图5所示。

图5 支座布置Fig.5 The arrangement of supports
根据结构的特点、边界支撑和斜拉索的布置情况,考虑到集中荷载在加载中的位置和有限元模型的修正目标,将梁段模型结构划分为32 个有限元模型单元,33 个节点,单元长度并不完全一致,单元划分情况如图3所示。
3.2 待修正参数的确定
在进行试验时,两侧弹簧支座放置较久,两侧弹簧支撑的刚度可能发生改变,且边界情况较为复杂。本试验将边界条件等效为两侧,仅有弹性支撑K1、K2 和纵桥向的水平约束。斜拉索受到重力作用出现垂度效应,导致设计参数与真实值有一定误差。因此,模型修正的对象是5根斜拉索的刚度和两侧竖向弹性支撑K1、K2 的刚度。其中,为保证斜拉索刚度的修正符合实际情况,具有物理意义,对索的刚度修正主要是对索的设计参数EA进行修正。

表3 待修正参数初值Table 3 The initial value of parameters
3.3 修正前的挠度偏差
在建立的初始有限元模型中,分别输入相应工况后,获得试验结构任意位置的挠度值,再将理论值和试验值进行对比。工况一和工况二其结果各取5个关键测点与试验测试值进行对比,分别见表4~5。由于测点数量较少,小于其计算响应的位移数。因此,根据试验数据拟合挠度曲线,拟合后的试验位移数与计算响应的位移数一致,在挠度变化曲线中更清晰呈现出理论值与试验值的挠度偏差,拟合后位移数为31个。2种工况的结果如图6~7所示。

表4 工况一作用下的挠度对比Table 4 The comparison of deflection under working condition one mm

表5 工况二作用下的挠度对比Table 5 The comparison of deflection under working condition two mm
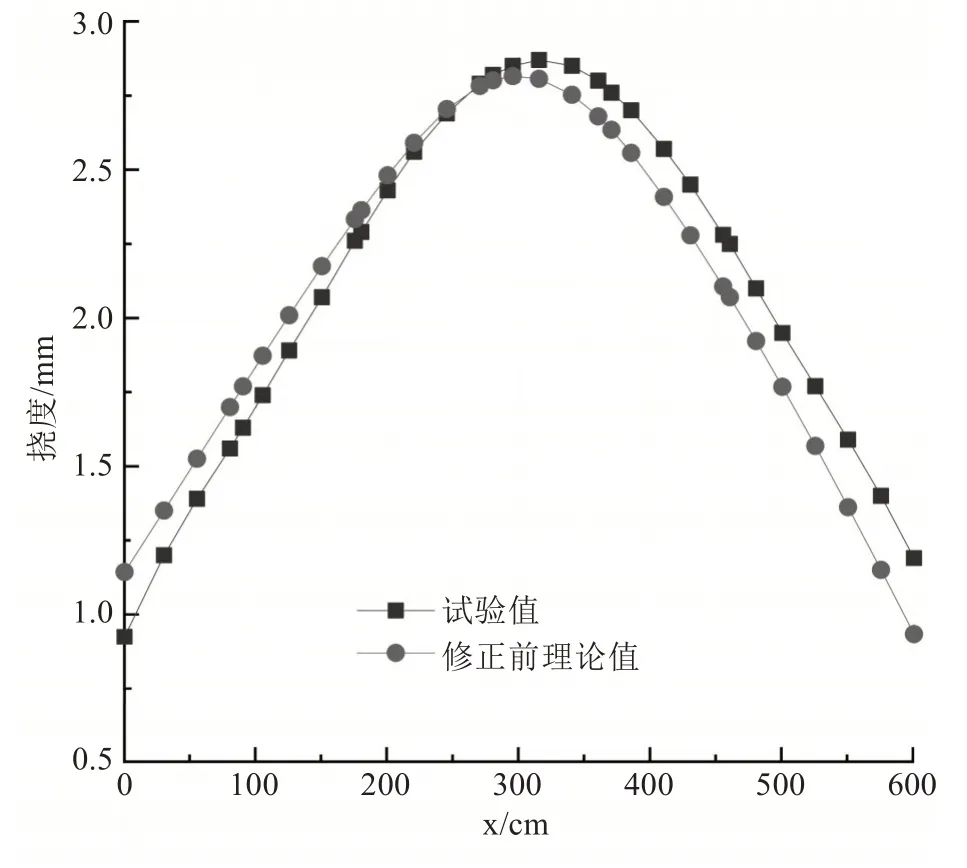
图6 工况一的挠度Fig.6 The deflection curve diagram under the action of working condition one

图7 工况二的挠度Fig.7 The deflection curve diagram under the action of working condition two
3.4 修正的过程及结果
根据目标函数,利用MATLAB 软件编写设计参数修正程序,对初始有限元模型进行修正,7 个参数βi(i= 1,2,···,7)为待修正参数,进行迭代计算,得出最优解。迭代过程中,由于目标函数达到最优解,迭代结束,共迭代113次,计算响应出左侧弹簧支撑K1、右侧弹簧支撑K2 和5 根斜拉索刚度的修正结果,见表6。目标函数变化曲线如图8所示。

表6 待修正参数的修正结果Table 6 The correction results of parameters 103 kN·m-1

图8 目标函数迭代趋势Fig.8 The iterative trend graph of objective function
工况一和工况二作用下,挠度优化结果取5个关键测点和试验值作对比,其详细挠度数值见表7~8。修正后的挠曲线和拟合后的试验值曲线进行对比,如图9~10所示。
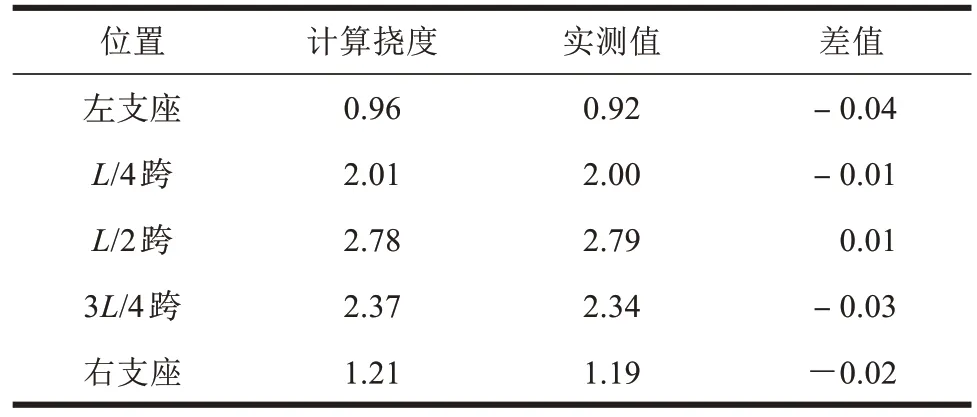
表7 工况一作用下的修正后挠度对比Table 7 The comparison of modified deflection under the action of working condition one mm

表8 工况二作用下修正后挠度对比Table 8 The comparison of modified deflection under the action of working condition two mm

图9 修正后工况一作用下的挠度Fig.9 The deflection curve diagram under the action of working condition one after modification

图10 修正后工况二作用下的挠度Fig.10 The deflection curve diagram under the action of working condition two after modification
从图9~10中可以看出,有限元模型经过修正后,理论挠度值与试验实测出的挠度值基本一致,最大挠度误差0.04 mm,远小于未优化前的有限元模型计算的挠度理论值与试验值的差值。表明:基于静载试验的有限元模型修正方法是可行性的,可以满足实际工程对精度的要求。
4 结论
1)根据设计方案或者竣工图纸中的设计参数,建立PPC 斜拉桥缩尺模型的初始有限元模型。在相应工况下,计算的理论值与静载试验的实测值有一定误差。表明:初始有限元模型需要修正后才能反映试验中的实际结构,满足工程校验的要求。
2)运用低阶模态参数构建柔度矩阵,因柔度矩阵在推导过程中与待修正参数直接相关,所以可以直接建立挠度变形与参数之间的灵敏度关系。PPC 斜拉桥缩尺模型的待修正参数,主要有5 根斜拉索的刚度和左、右两侧弹簧支撑K1、K2 的刚度。
3)通过2 种不同工况下的试验数据,验证了该方法的可行性,修正后的PPC 斜拉桥有限元模型值与静载试验实测值更吻合。基于静载试验的有限元模型修正技术,利用模态柔度原理有效修正了初始有限元模型,建立了该结构基准有限元模型,具有效率高、拟合快、计算误差较小等优点,可满足工程应用要求。

