功能反应函数的演化对食饵捕食系统动力学的影响

王玉億，邹 兰

（四川大学 数学学院，四川 成都 610064）

研究食饵捕食系统

其中，α 表示食饵出生率，βx 表示由食饵种族内部竞争带来的食饵密度变化率，γ 表示捕食者死亡率，k表示捕食者将捕食的食饵转化为自身增长的效率.x（t）和y（t）分别表示食饵和捕食者在时间t时的密度分布，由系统（1）的生物学意义可知

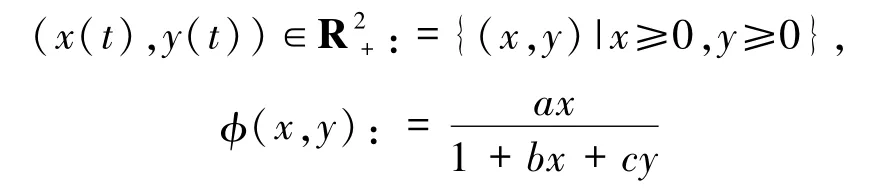
为Beddington-DeAngelis功能反应函数，表示在每单位时间、每单位捕食者的捕食下食饵密度的变化，也称作捕食率，其中a，b ＞0.当c ＝0 时，

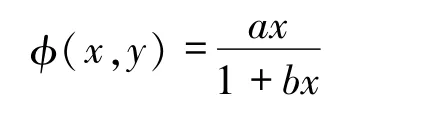
为经典的Holling II 型功能反应函数，bx 表示捕食率的增幅随x增加而下降；当c ＞0 时，cy 表示捕食率随y增加而下降.

食饵捕食系统的动力学行为一直受到学者的关注［1-8］，其中具有Holling II型功能反应的食饵捕食系统也称为“R-M”模型.陈兰荪等［9］用微分方程定性分析方法对“R-M”模型作了详细分析，并讨论了极限环的存在性和唯一性.对于Beddington-DeAngelis型功能反应，Cantrell等［10］指出c影响正平衡点的位置和稳定性，且当c 充分小时，系统大致上与c ＝0 时的系统表现出相似的动力学性质；Hwang［11］证明了正平衡点局部渐进稳定与全局渐近稳定相一致，并归纳了正平衡点全局渐稳的情况，证明了极限环的唯一性［12］；Zhang等［13］讨论了系统（1）的Hopf分岔，给出的分岔值是多个参数的一个复杂形式；文献［14］也讨论了系统（1）的Hopf分岔，整理出了相对简单的分岔参数与分岔值，该值仍是多个参数的表达式；文献［15］的结果更清晰全面地总结边界平衡点的局部与全局渐稳，研究了边界平衡点存在跨临界分岔及正平衡点的Hopf 分岔，给出分岔参数.由于平衡点坐标形式复杂，表达式使用隐式形式，分岔依赖于许多参数的一个复杂表达式.另一方面，前人工作中多是考虑c ＞0 的情况.由于可能存在部分特殊的群居捕食者进行合作捕食，捕食率随y增加而上升，这对应着c ＜0.

本文着重探索φ（x，y）中有无cy项对系统（1）的动力学行为的影响，即功能反应函数从Holling II型演化为Beddington-DeAngelis 型时动力学行为的变化.具体地，考虑c 从0 变为充分小的数（正或负）时系统（1）的动力学行为有无变化，从而对文献［10］中关于“系统在c为充分小正数时大致上具有与c ＝0 时相似的动力学性质”的注释给出严格数学推导，并研究c 为充分小负数时的动力学变化.此外，通过Poincaré变换分析无穷远点的性质，讨论全退化无穷远点附近的轨线走向，结合文献［12］中关于全局稳定性的结果，给出全局相图.

1 平衡点分析

令

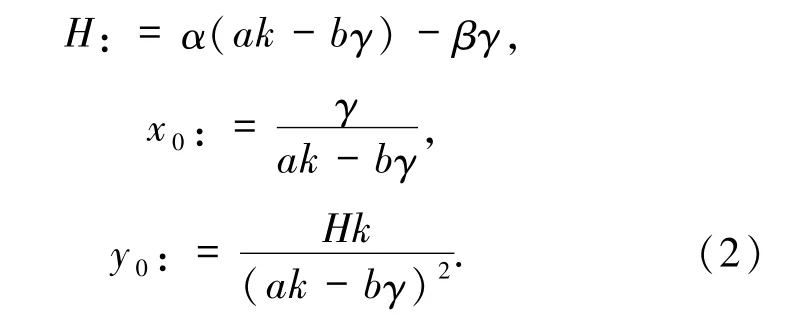
直接计算易知，当c ＝0 时，系统（1）的平衡点类型如表1 所示.

表1 c ＝0 时系统（1）的平衡点类型Tab.1 Types of equilibria in system（1）when c ＝0

当c≠0 时，发现系统（1）至多3 个平衡点，且其中2 个（O，E1）与c ＝0 时位置一样.下面要进一步确定这2 个平衡点类型是否发生变化，第3 个平衡点是否存在，及其位置类型与E2有何关系.

定理1.1当c≠0 且充分小时，系统（1）的平衡点O和E1的类型与表1 中完全一致，即c 在0附近变化不影响O和E1的类型.

证明下面仅对H ＝0 时证明E1的鞍结点类型不变，其他情形类似可证.令

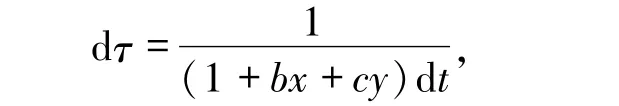
仍用t表示时间，则系统（1）化为

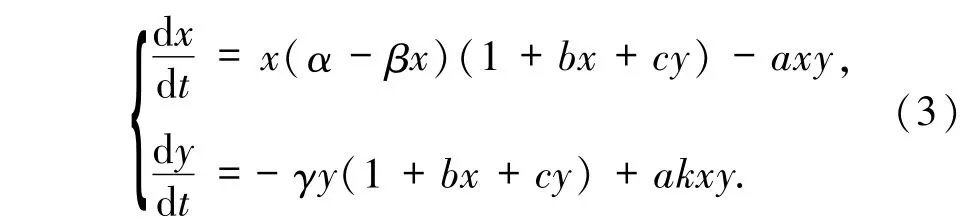
计算可得系统（3）在平衡点E1处的雅可比矩阵的特征值为

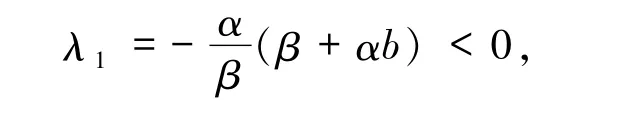
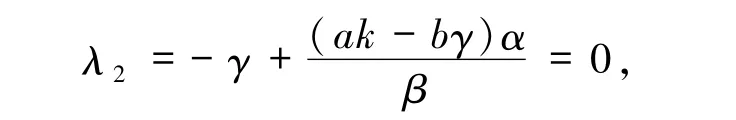
即E1是一个退化平衡点.做变换

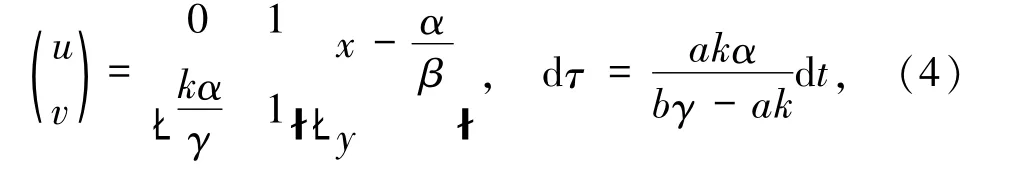
并仍将时间变量写作t，则系统（3）化为

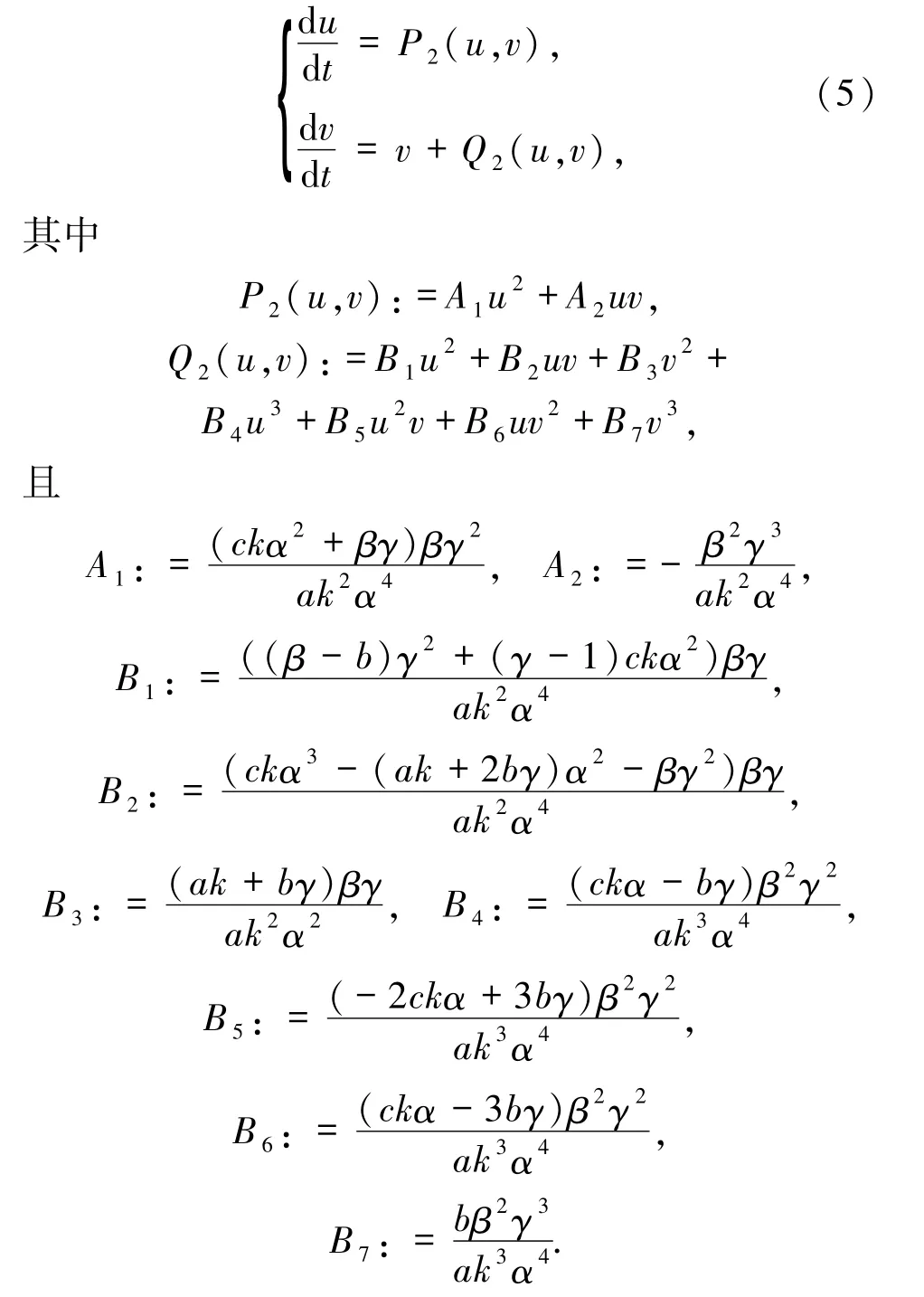
如同文献［16］的做法，由隐函数定理可知，存在解析函数φ（u）使得

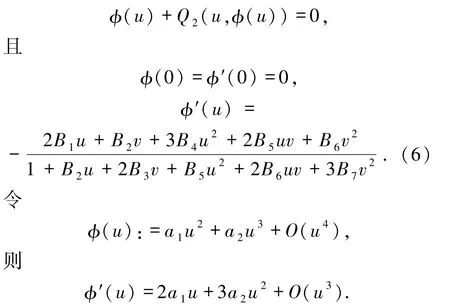
把φ′（u）代入（6）式的左边，并用φ（u）代替（6）式中的v，通过比较u的各次幂的系数可解得

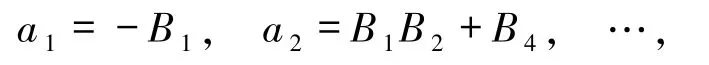
从而获得φ（u）的级数表达式.令ψ（u）：＝P2（u，φ（u）），计算可得

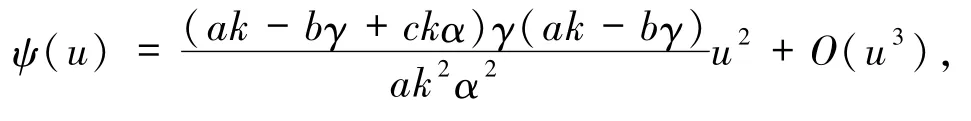
可见ψ（u）二次项的系数为正.由文献［16］可知，系统（5）的原点（0，0）是鞍结点.因此，系统（1）的退化平衡点E1是鞍结点.

下面判断鞍结点E1附近的轨线走向.取vu 平面的坐标轴上两点M（1，0）、N（0，1），根据变换（4）可计算得M对应于xy平面上一点M′（m，0），N 对应于xy平面上一点N′（n，1），其中

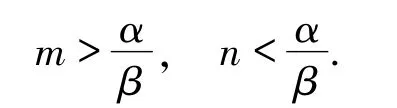
由此可知，vu平面的坐标轴返回到xy平面时，坐标轴位置如图1（a）所示.在vu 平面上，当u ＝0 时，dv／dt的符号由v 的符号决定，当v ＞0 时，dv／dt ＞0；当v ＜0时，dv／dt ＜0；当v ＝0时，du／dt 符号由A1u2的符号决定.由于A1＞0，因此du／dt ＞0.由此可得vu平面上鞍结点O 附近坐标轴上的轨线走向，见图1（b）.注意到，在变换（4）中，

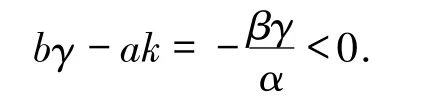
因此，时间变换是反向的，从vu 平面返回xy 平面时，轨线方向相反.从而可得xy 平面鞍结点E1附近的轨线走向，易知鞍结点的结点结构位于第一象限，鞍点结构位于第四象限，见图1（c）.

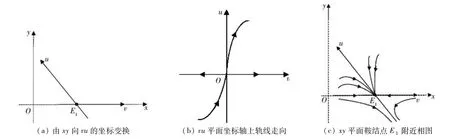
图1 坐标变换示意图Fig.1 Schematic diagrams for coordinate transformation

定理1.2当c≠0 且充分小时，系统（1）存在第3 个平衡点（x1，y1）的充要条件是H ＞0.当H ＞0时，（x1，y1）的类型与E2相同，且其位置趋于E2（c→0），其中

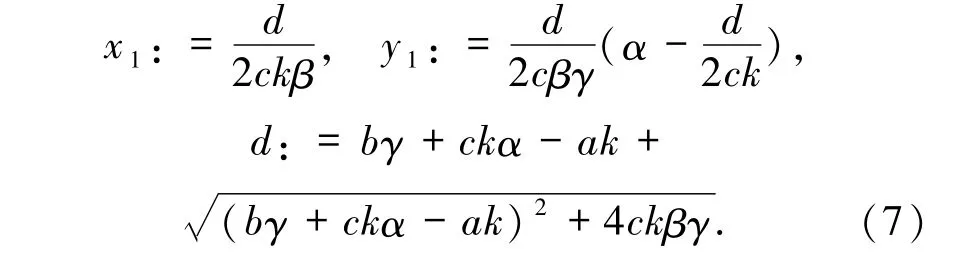
证明系统（1）的平衡点是方程组

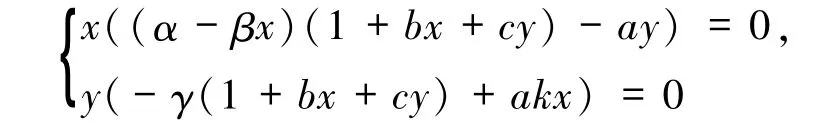
的解.由于xy ＝0 时，有2 个平衡点O和E1，因此只需考虑xy≠0.易知，第3 个平衡点存在当且仅当

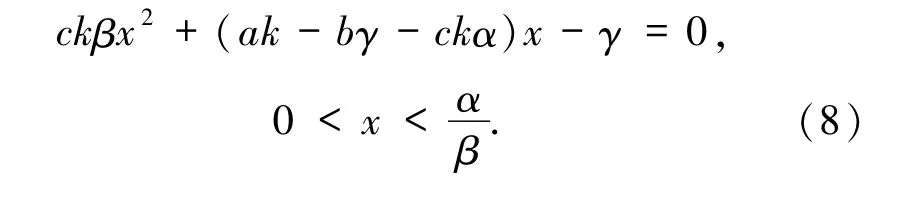
进一步，（8）式有解，当且仅当H ＞0，（8）式可得第3 个平衡点（x1，y1），其中x1、y1的表达式在（7）式中给出.

当c ＝0 时，系统（1）有第3 个平衡点E2（x0，y0）.由x1、y1的表达式可知

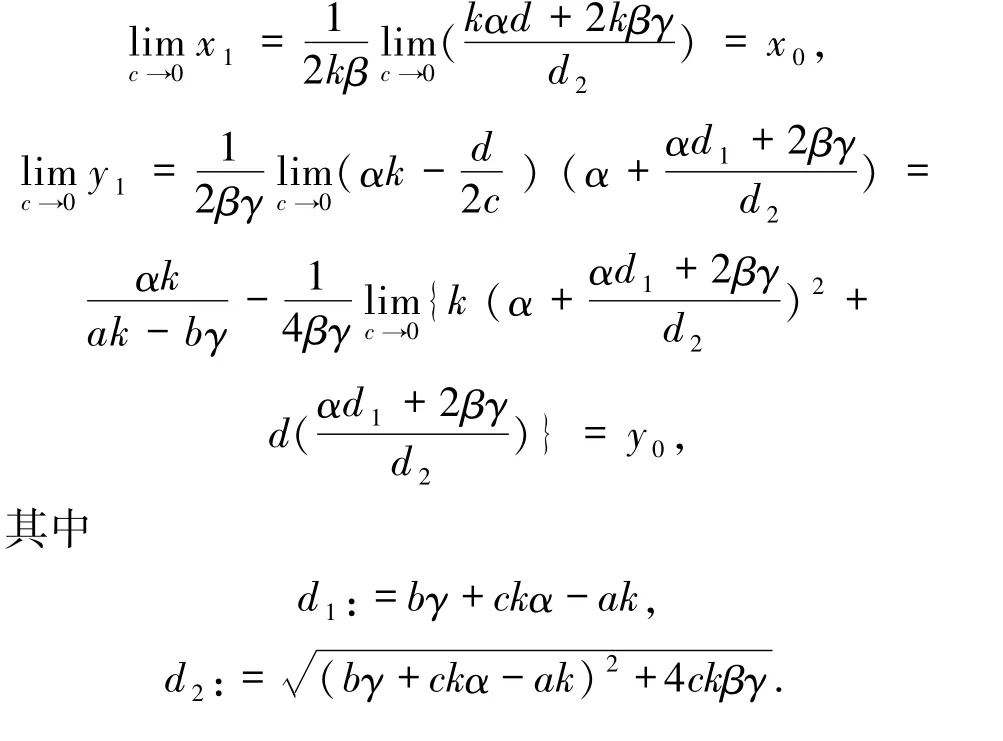
当c ＝0 时，易知系统（3）在平衡点E2处的雅可比矩阵为

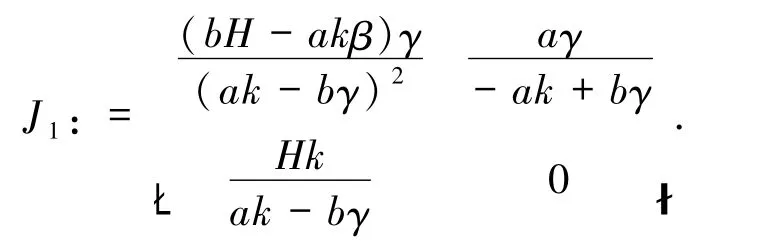
当c≠0 时，系统（3）在平衡点～E2（x1，y1）处的雅可比矩阵为

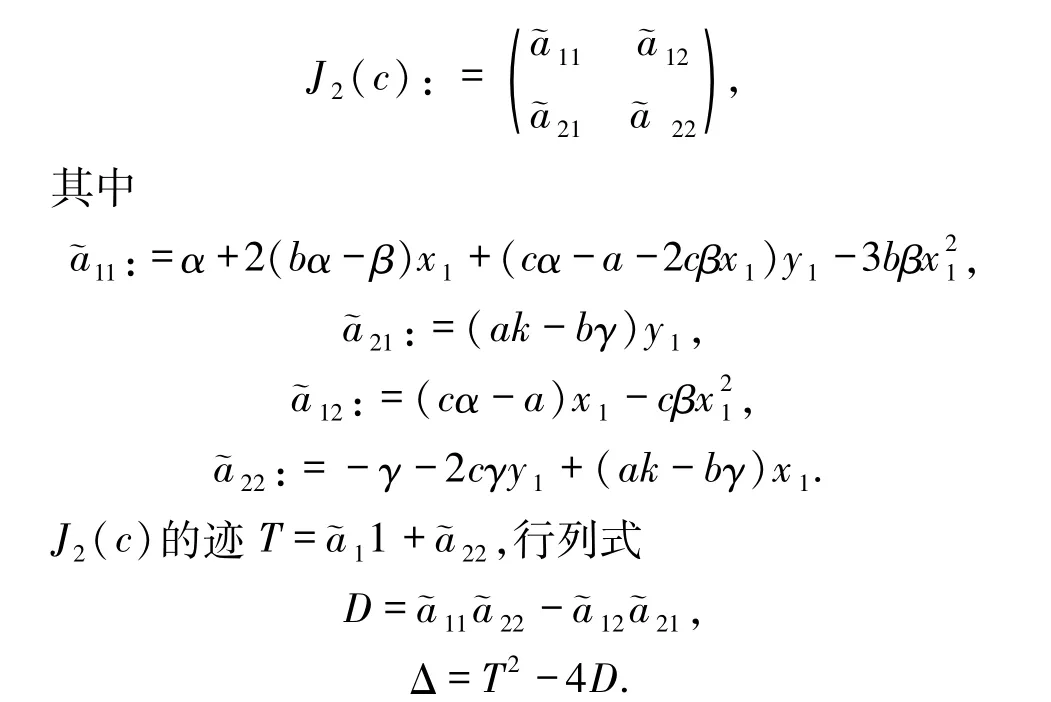
由于当c→0 时，（x1，y1）→（x0，y0），计算可知c→0时，J2（c）→J1.另一方面，E2不会是中心（见表1）.因此，当c充分小时，与E2具有相同类型.

由定理1.1 和1.2 已知，c 在0 附近的变化并不影响平衡点类型和位置.虽然与E2的位置并不相同，但是→E2（c→0），所以可以看成位置不改变.定理1.1 和1.2 并没有给出c在0 附近的变化对平衡点稳定性的影响.实际上，由于O和E1的稳定性判定中不涉及c的值（见定理1.1 的证明），所以c在0 附近的变化对O和E1的稳定性并无影响.然而，c在0 附近的变化是可能对第3 个平衡点的稳定性产生影响的，继而导致分岔的出现.下面将详细讨论这一点.

2 分岔分析

如表1 所示，H ＞0 时才有第3 个平衡点，因此假设H ＞0.当E2为结点或粗焦点时，参数c在0 附近的变化并不改变其稳定性，即～E2与E2的稳定性相同.下面的定理是针对E2为一阶细焦点的情形.从雅可比矩阵J1（见定理1.2 的证明）的表达式，易知E2为一阶细焦点当且仅当

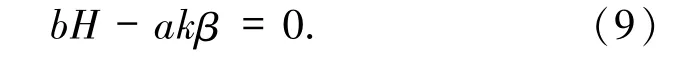
定理2.1设系统（1）满足（9）式.当c从0 变为充分小的负值时，系统（1）发生Hopf 分岔，唯一一个极限环分岔出来.这个极限环是稳定的且围绕.当c从0 变为充分小的正值时，系统（1）不发生Hopf分岔.

证明如同定理1.1 的证明，只需考虑系统（1）的等价系统（3）.对（3）式做平移变换

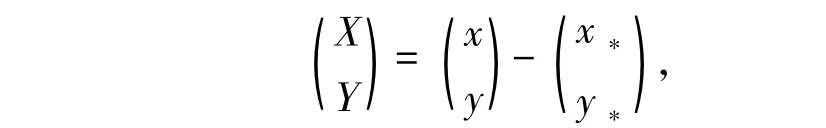
并将X、Y写作x、y，得

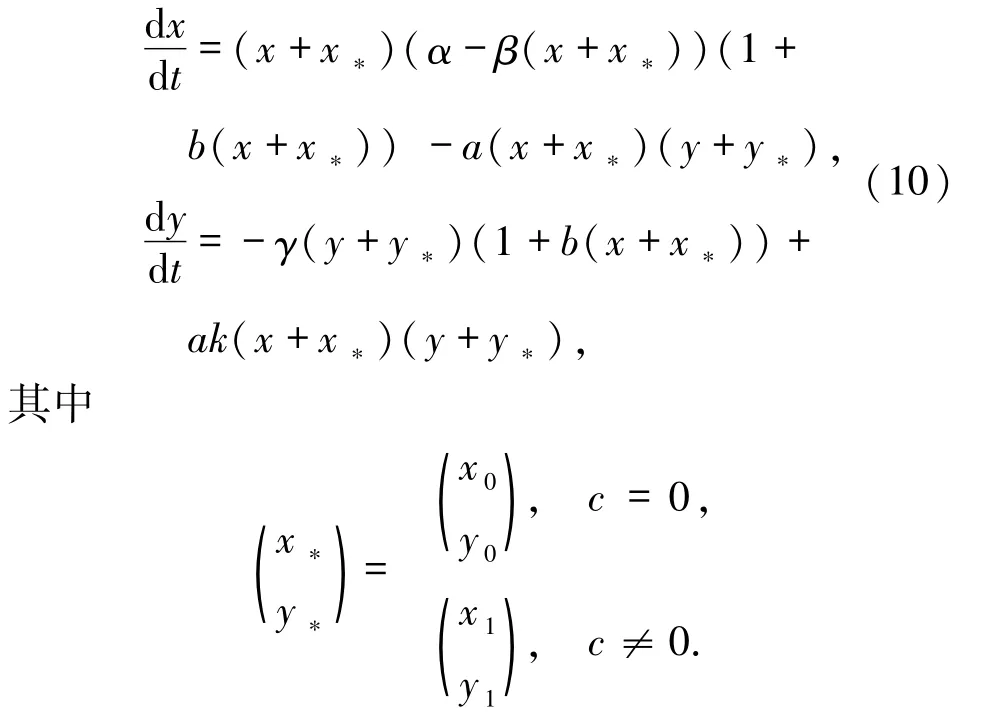
把系统（10）在O（0，0）的雅可比矩阵记为J（c）.因此

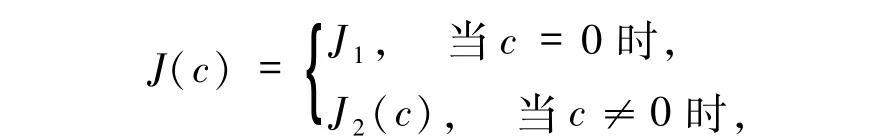
其中J1、J2（c）在定理1.2 的证明中给出.由于当c→0时，J2（c）→J1，因此J（c）是连续的.令

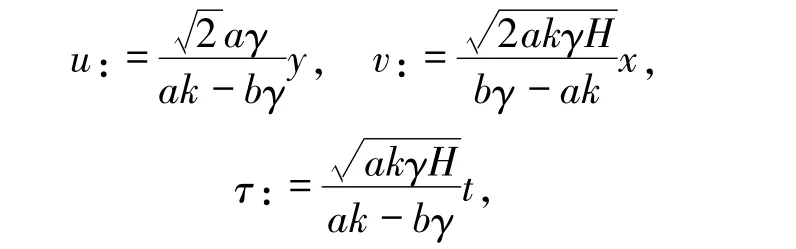
系统（10）|c＝0化为

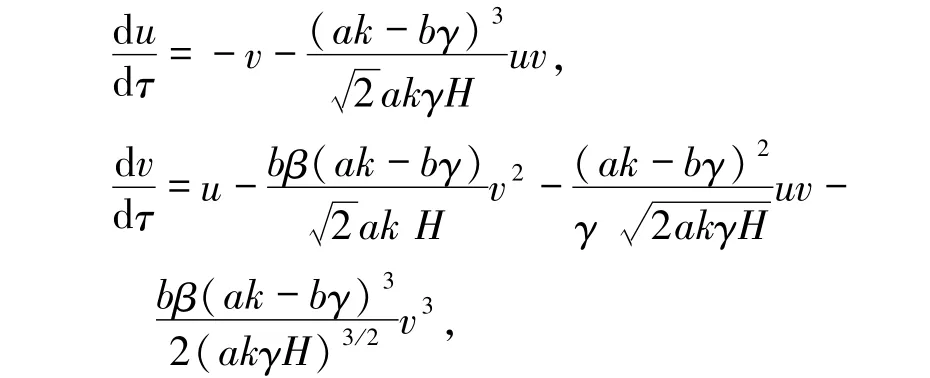
其中H的表达式在（2）式中给出.由于此系统为中心型，计算其一阶焦点量g3，得

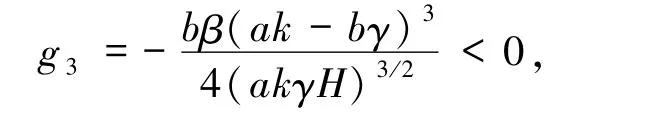
因此O是系统（10）|c＝0的一阶稳定细焦点.由J（c）的连续性，当c≠0 且充分小时，系统（10）的平衡点O仍为焦点.由J2（c）的表达式可计算其迹T（c）在c ＝0 处的导数得

记J2（c）特征值的实部为μ（c）.因此，μ（0）＝0 且

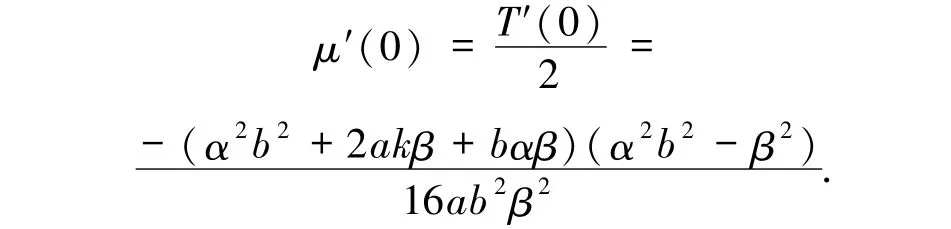
又由（9）式可知

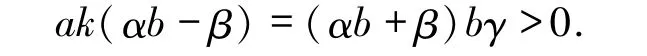
因此，μ′（0）＜0.从而c从0变为充分小的正常数时，系统（10）的平衡点O从稳定一阶细焦点变为稳定粗焦点，不发生Hopf分岔.当c从0变为充分小的负常数时，系统（10）的平衡点O从稳定一阶细焦点变为不稳定粗焦点，发生一阶Hopf 分岔，唯一一个极限环从O分岔出来，且此极限环是稳定的.

一方面，系统（1）的Hopf 分岔在文献［13-15］中给出，由使用的c为正且分岔参数是多个参数复合的形式，并不能确定是哪个参数变动导致Hopf分岔.结合定理2.1 可知，该Hopf 分岔不是由c从0 变为充分小的正值产生的.另一方面，在文献［15］中，系统（1）的鞍结点E1被证明存在跨临界分岔.结合我们定理1.1 可知此跨临界分岔不是由c从0 向充分小的非零数变动导致的，即c 在0 附近变化时，系统（1）不发生跨临界分岔.

3 无穷远分析

根据文献［10-12］中关于系统（1）全局稳定性的结果，当系统（1）不存在正平衡点时，全局渐进稳定，此时对应H≤0.本文定理1中H ＝0时鞍结点E1在第一象限内的结点结构与该结论相一致.另一方面，当系统（1）存在正平衡点时，如果～E2为稳定结点或稳定焦点，即～E2局部渐进稳定，则全局渐进稳定；如果～E2为不稳定结点或不稳定焦点，则有且只有一个极限环，且极限环是稳定的，此时对应H ＞0.

下面分析系统（1）无穷远处轨线的走势.

定理3.1系统（1）在第一象限内有2 个无穷远平衡点A：（+∞，0）和B：（0，+∞），其中A为不稳定结点，B 为全退化平衡点.当cα -a ＝0 时，有无数条轨线沿离开B，单位圆周Γ上的轨道离开A趋近B.

证明对系统（3）做Poincaré变换，令

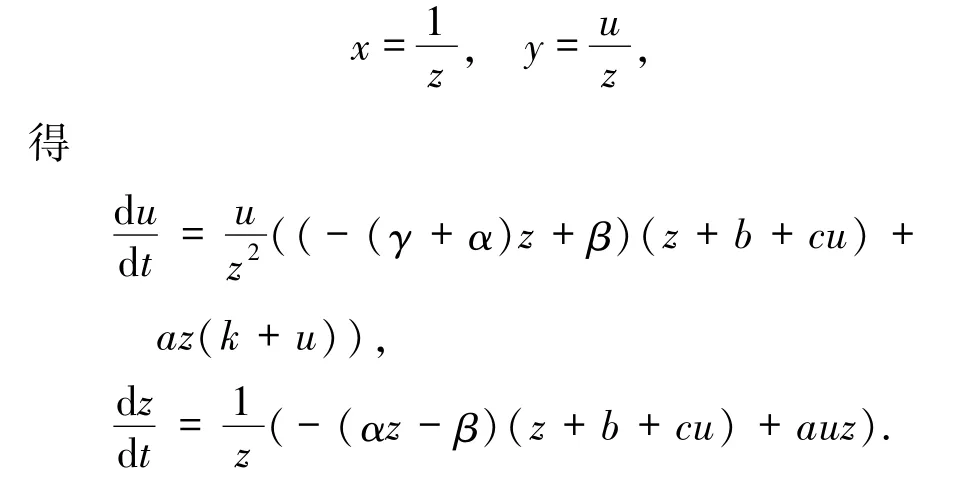
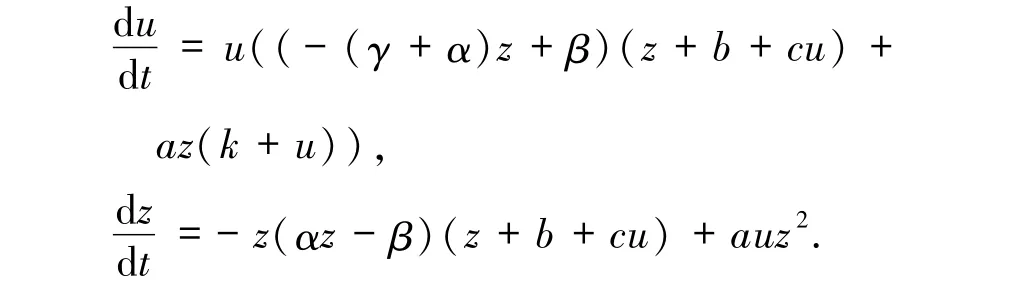
在α*平面上解出z ＝0 时的奇点是Q1（0，0）、Q2（-b／c，0）.Q1处雅可比矩阵的迹T1＝2βb ＞0，行列式

且特征矩阵对应于特征值βb 有无穷多特征向量，因此Q1是不稳定星形结点；Q2处雅可比矩阵的迹T2＝-βb ＜0，行列式D2＝0，因此平衡点Q2为退化平衡点.由于Q2返回到xy 平面后，不在第一象限内，不做具体讨论.此外，z ＝0 也是解，故赤道由奇点和轨线连成.

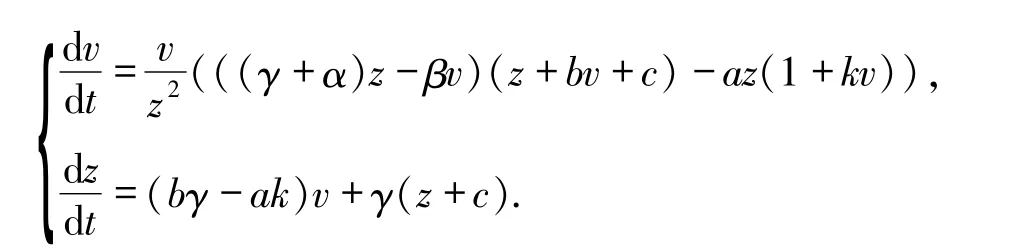
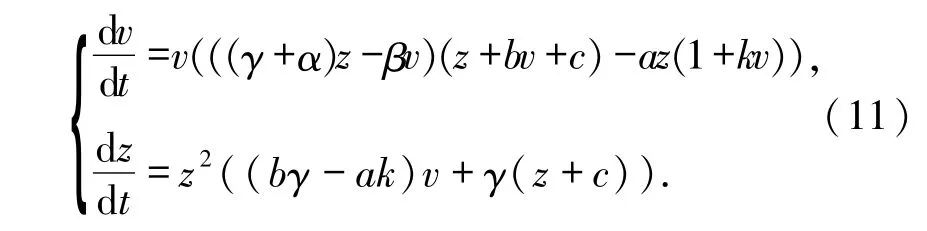
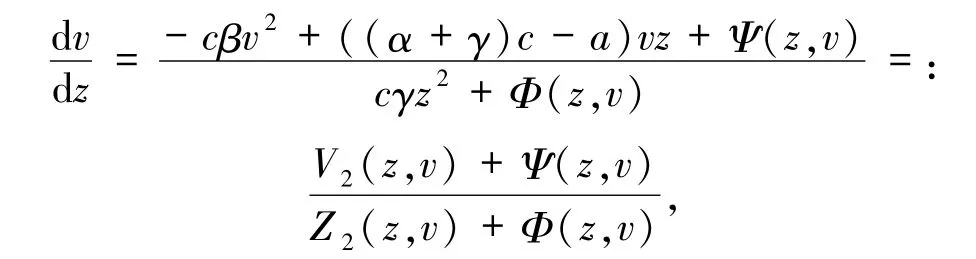
其中，Z2、V2分别是z和v的二次齐次多项式，

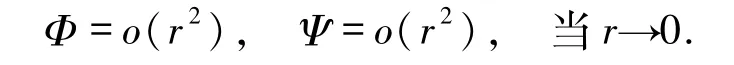
示性方程

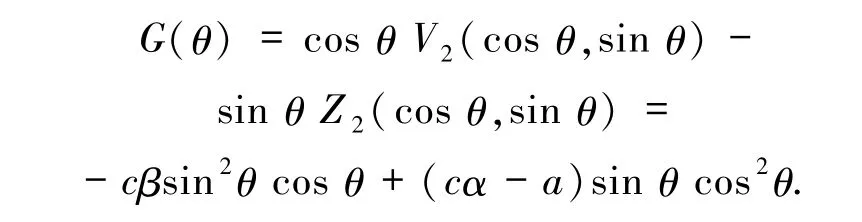
当cα-a ＝0 时，G（θ）＝-cβsin2θ cos θ.此时，示性方程有单根，有二重根θ3＝0 和θ4＝π.记

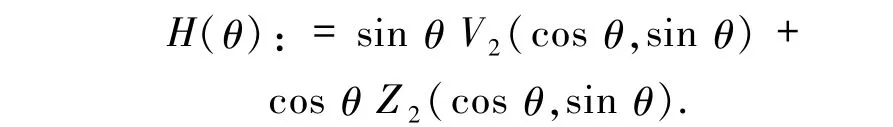
对于θ3＝0 和θ4＝π，θ3、θ4不是H（θ）＝0 的根，

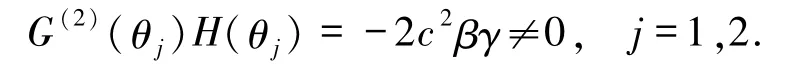
已知Φ（z，v）、Ψ（z，v）在（0，0）附近是z、v的解析函数，所以满足文献［16］的条件，从而在zv平面上，沿着各只有唯一轨线进入奇点Q3，有无数条轨线分别沿θ3＝0，θ4＝π 进入奇点Q3（此处及后文中的“进入”均指，当t→+∞或t→-∞时，轨线趋近于平衡点）.将zv 平面变换为vz平面，则有无数条轨线分别沿进入奇点Q3，沿着θ3＝0，θ4＝π 各只有唯一轨线进入奇点Q3.

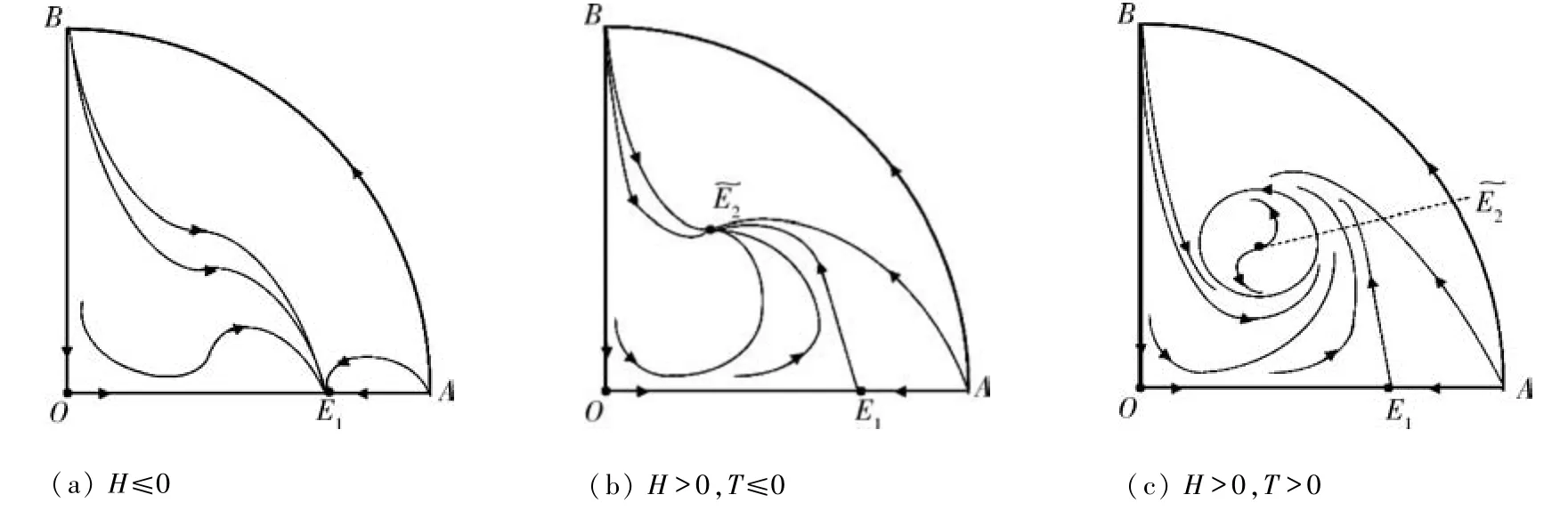
图2 cα-a ＝0 时，系统（1）全局相图Fig.2 Global phase diagrams of system（1）when cα-a ＝0