最优少重量二元码的构造

任 磊，廖群英

（四川师范大学 数学科学学院，四川 成都 610066）

其中Ai（1≤i≤n）为码中汉明重量为i的码字个数.序列（1，A1，A2，…，An）为码的重量分布.若序列（A1，A2，…，An）中非零Ai（1≤i≤n）的个数为t，则称码为t权重二元码.

设p为素数，q ＝pn，q是q 元有限域，qk为有限域q的k 次有限扩张.令D ＝｛d1，d2，…，dn｝⊆qk，记Tr（x）＝x +xq+… +xqk-1为有限域qk到q上的迹映射，则可得到q上码长为n 的线性码

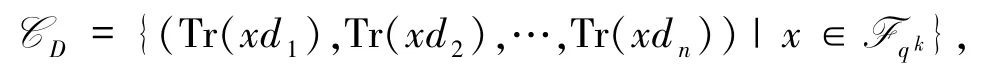
Ding 等［1-2］第一次给出利用定义集构造线性码的一般方法，随后众多学者通过选取合适的定义集构造了许多码［3-6］，并且这些码能够应用于密钥共享方案［7］和身份认证［8］.

设R是有限交换环，Rm是环R的m（m≥2）次扩张，是Rm的乘法群.定义

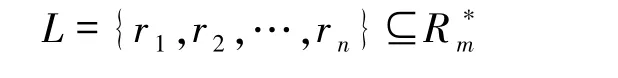
上的迹码为

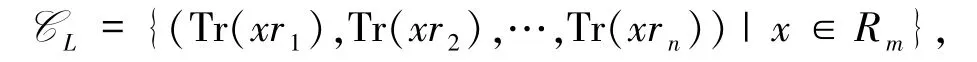
其中Tr（·）是Rm到R的一个R-线性函数.基于上述构造方法，学者们给出许多定义在环上的少重量线性码［9-17］.

设m（m≥2）是正整数，向量v ＝（v1，v2，…，vm）∈的支撑集定义为

则向量v的汉明重量为wt（v）＝|Supp（v）|.2［m］为［m］＝｛1，2，…，m｝的幂集.定义到2［m］的一个映射如下：

且|A／B|表示集合A／B中元素的个数.

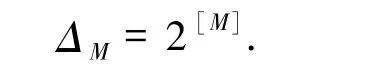
对于参数为［n，k，d］2的一个二元码，若参数满足Griesmer界，即

2019 年，Hyun等［17-18］利用简单复合体构造了最优二元有限族和极小线性码；随后，2020 年，Wu等［19］运用简单复合体，构造了环2+u2上2 类少重量线性码.基于他们的工作，本文在有限域2上利用简单复合体构造了2 类最优少重量二元码，给出了2 类码的重量分布，并证明了它们的参数都满足Griesmer界.

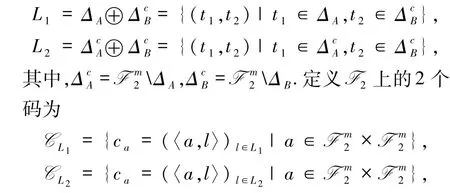
1 预备知识

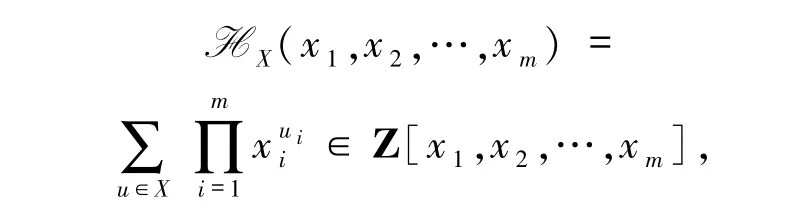
其中u ＝（u1，u2，…，um），且Z是整数环.

为计算码的重量分布，先给出如下引理.

引理1.1［17］设Δ⊆是中的一个简单

复合体，则

在本文中，2 个简单复合体

设a ＝（α，β），l ＝（t1，t2），其中α ＝（α1，α2，…，αm），β ＝（β1，β2，…，βm）∈，t1∈ΔA，t2∈.若a ＝0，则ωH（ca）＝0.因此，不妨设a≠0，此时由L1的定义可得

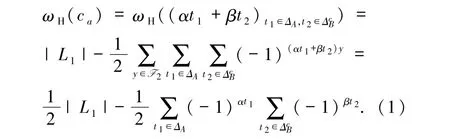
定理2.1设A，B⊆［m］且0 ＜|B| ＜m.若ΔA、ΔB是m2的2 个简单复合体，，则码L1的码长为2|A|（2m-2|B|），码字个数为2m+|A|，且重量分布如表1 所示.

表1 码L 1的重量分布Tab.1 Weight distribution of code L 1

表1 码L 1的重量分布Tab.1 Weight distribution of code L 1

再由（1）式可得

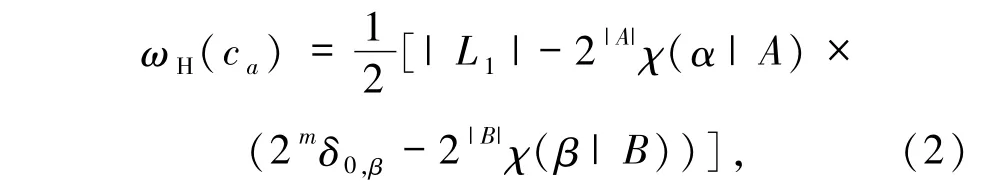
其中δ是符号函数.

设X ＝Supp（α），Y ＝Supp（β），下面分2 种情形讨论.

情形1若β ≠0，此时由（2）式可得

1）若χ（α|A）χ（β|B）＝1，则

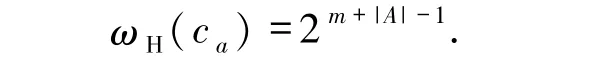
又由χ（α|A）χ（β|B）＝1，可知X∩A ＝Y∩B ＝∅.而Y≠∅，故X∩A ＝∅，Y∩B ＝∅，Y≠∅.记

故码字个数为|T0| ＝2m-|A|（2m-|B|-1）.

2）若χ（α|A）χ（β|B）＝0，则

又χ（α|A）χ（β|B）＝0，故X∩A≠∅或Y∩A≠∅且Y≠∅.记

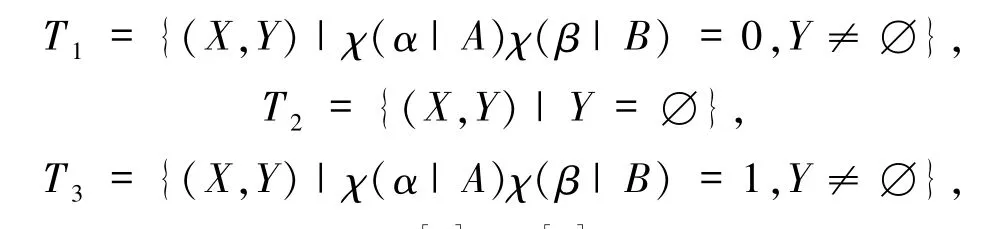
从而T1∪T2∪T3＝2［m］×2［m］.又

从而|T1| ＝22m-|T2| -|T3|，故码字个数为

情形2若β ＝0，此时由（2）式可得

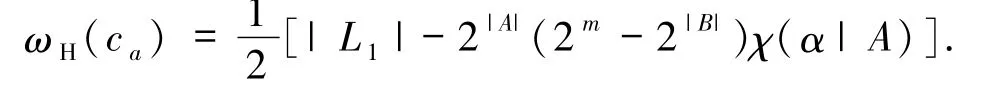
1）若χ（α|A）＝1，则ωH（ca）＝0.又χ（α|A）＝1，故X∩A ＝∅.再由Y ＝∅以及X，Y≠∅，可知X≠∅.记

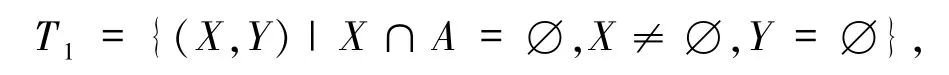
故码字个数为|T1| ＝2m-|A|-1.

2）若χ（α|A）＝0，则

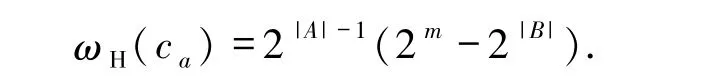
又χ（α|A）＝0，故X∩A≠∅，从而X∩A≠∅，Y ＝∅.记T0＝｛（X，Y）|X∩A≠∅，Y ＝∅｝，故码字个数为2m-2m-|A|.

定理2.2码L1是最优二元码.

证明由定理2.1 可知，码L1的参数为［2|A|（2m-2|B|），m+|A|，2|A|-1（2m-2|B|）］2，故

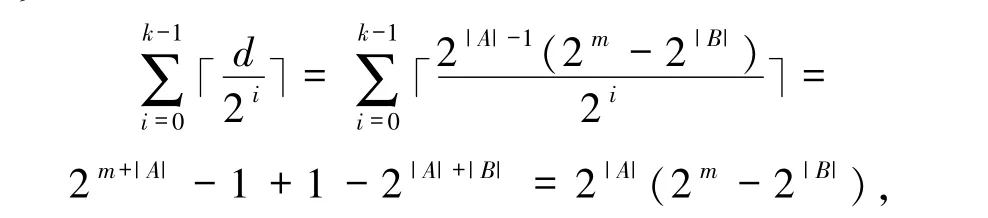
2.2 码L2的重量分布设a ＝（α，β），l ＝（t1，t2），其中α ＝（α1，α2，…，αm），β ＝（β1，β2，…，βm）∈，t1∈，t2∈.若a ＝0，则ωH（ca）＝0.因此，不妨设a≠0，此时由L2的定义可得

定理2.3设A，B⊆［m］且0 ＜|A|，|B| ＜m.若ΔA、ΔB是的2 个简单复合体，，则码L2的码长为（2m-2|A|）（2m-2|B|），码字个数为22m，且重量分布如表2 所示.

表2 码L 2的重量分布Tab.2 Weight distribution of code L 2

表2 码L 2的重量分布Tab.2 Weight distribution of code L 2

证明由定义容易知道码L2的码长为|L2| ＝（2m-2|A|）（2m-2|B|）.设0≠a ＝（α，β），其中α ＝（α1，α2，…，αm），β ＝（β1，β2，…，βm）∈.由（3）式可得

设X ＝Supp（α），Y ＝Supp（β），下面分4 种情形讨论.

情形1若α ＝0且β ≠0，则由（4）式可得［| L2| +（2m-2|A|）2|B|χ（β| B）］.

1）若χ（β|B）＝1，则

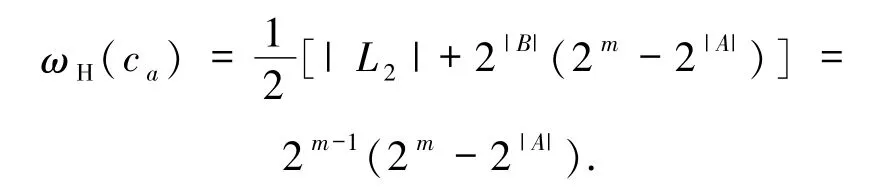
由χ（β| B）＝1，可知Y ∩B ＝∅.又α ＝0，β ≠0，故X ＝∅，Y ≠∅，从而Y ∩B ＝∅，Y ≠∅且X ＝∅.若记

T1＝｛（X，Y）| Y ∩B ＝∅，Y ≠∅，X ＝∅｝，故码字个数为|T1| ＝2m-|B|-1.

2）若χ（β|B）＝0，则

由χ（β| B）＝0，可知Y ∩B ≠∅.又α ＝0，β ≠0，故X ＝∅，Y ≠∅，从而Y ∩B ≠∅且X ＝∅.若记

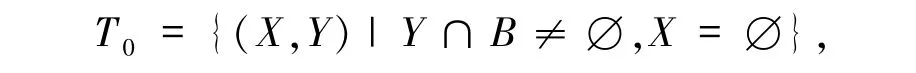
故码字个数为|T0| ＝2m-2m-|B|.

情形2若α ≠0且β ＝0，则由（4）式可得

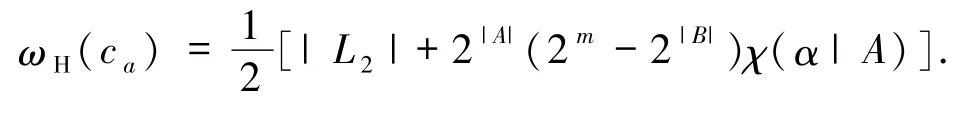
1）若χ（α|A）＝1，则

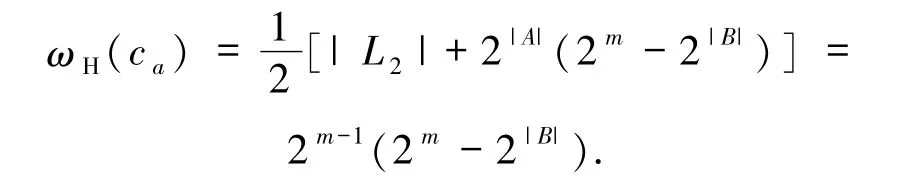
由χ（α|A）＝1，可知X∩A ＝∅.又α≠0，β ＝0，故X≠∅，Y ＝∅，从而X∩A ＝∅，X≠∅且Y ＝∅.若记

T1＝｛（X，Y）| X ∩A ＝∅，X ≠∅，Y ＝∅｝，故码字个数为|T1| ＝2m-|A|-1.

2）若χ（α|A）＝0，则

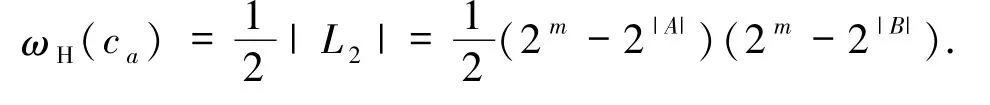
由χ（α|A）＝0，可知X∩A≠∅.又α≠0，β ＝0，故X≠∅，Y ＝∅，从而X∩A≠∅且Y ＝∅.若记

故码字个数为|T0| ＝2m-2m-|A|.

情形3若α ＝β≠0，则由（4）式可得

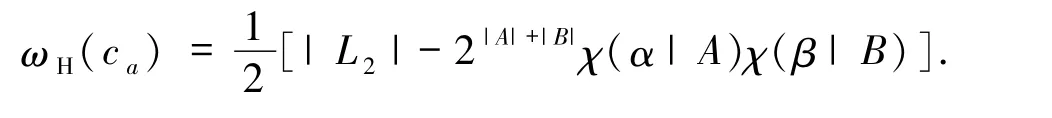
1）若χ（α|A）χ（β|B）＝1，则

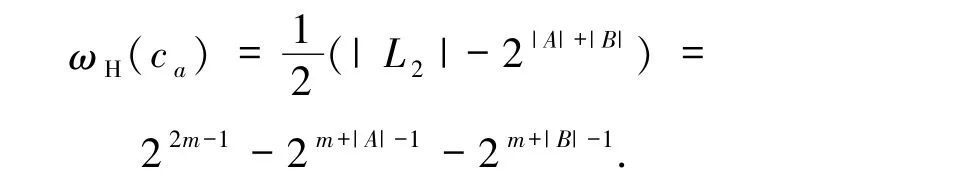
由χ（α|A）χ（β|B）＝1，可知X∩A ＝∅，Y∩B ＝∅.又α ＝β≠0，故X ＝Y≠∅，从而X∩（A∪B）＝∅且X≠∅.若记

故码字个数为|T1| ＝2m-|A∪B|-1.

2）若χ（α|A）χ（β|B）＝0，则

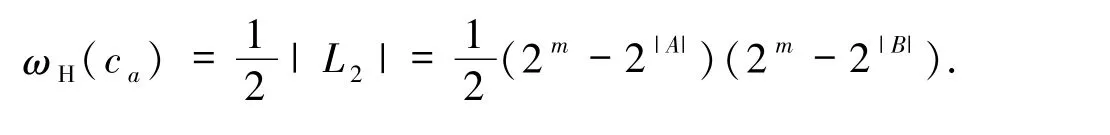
由χ（α|A）χ（β|B）＝0，可知X∩A≠∅，Y∩B≠∅.又α ＝β≠0，故X ＝Y≠∅，从而X∩（A∪B）≠∅且X≠∅.若记

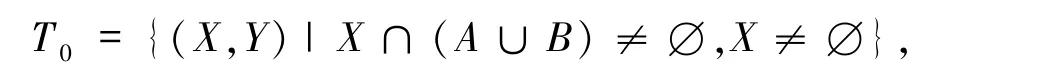
故码字个数为|T0| ＝2m-2m-|A∪B|.

情形4若α ≠β，α ≠0，β ≠0，则由（4）式得

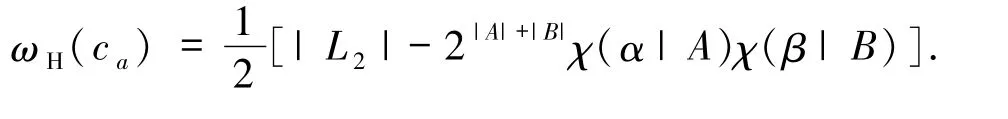
1）若χ（α|A）χ（β|B）＝1，则

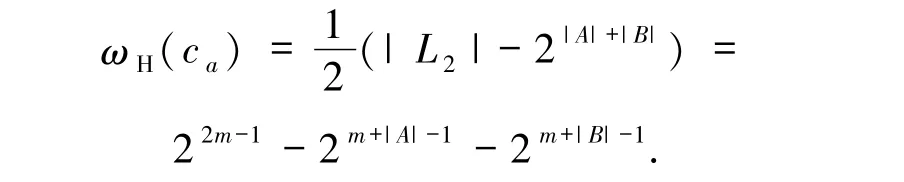
由χ（α| A）χ（β| B）＝1，知X ∩A ＝Y ∩B ＝∅.又α ≠β，α ≠0，β ≠0故X ≠Y，X ≠∅且Y ≠∅.令

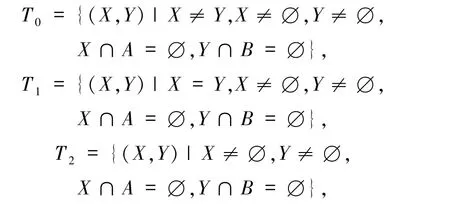
则由T2＝T1∪T0及| T2| ＝| T1|+| T0|，可得|T0| ＝|T2| -|T1|.故码字个数为

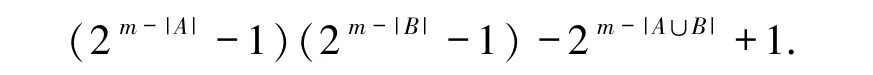
2）若χ（α|A）χ（β|B）＝0，则

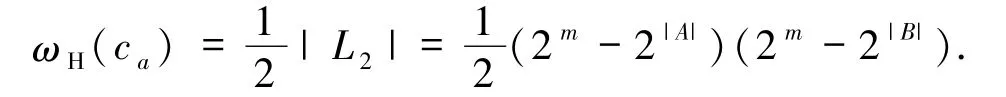
由χ（α|A）χ（β|B）＝0，可知χ（α|A）＝0，χ（β|B）＝1或χ（α|A）＝1，χ（β|B）＝0或χ（α|A）＝0，χ（β|B）＝0.

当χ（α| A）＝1，χ（β| B）＝0时，可得X ∩A ＝∅，Y ∩B ≠∅.又α ≠β，α ≠0，β ≠0，故X ≠Y，X ≠∅，Y ≠∅.令

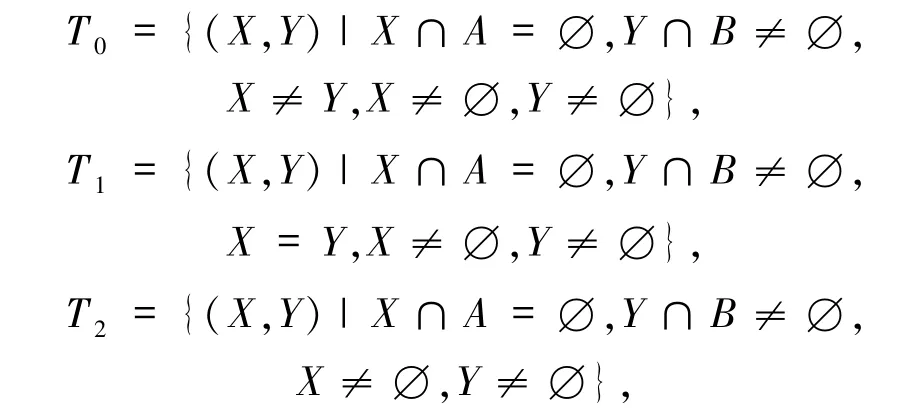
则由T2＝T0∪T1及|T2| ＝|T0|+|T1|，可知|T0| ＝|T2| -|T1|.又|T2| ＝（2m-|A|-1）（2m-2|B|），|T1| ＝2m-|A|（2|B／A|-1），从而

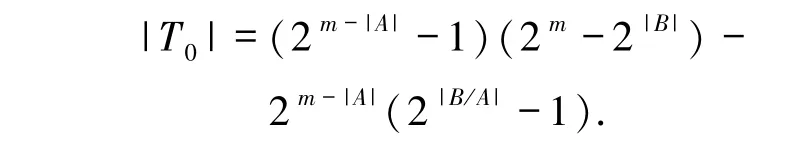
当χ（α| A）＝0，χ（β | B）＝1 时，易得X ∩A ≠∅，Y ∩B ＝∅.又α ≠β，α ≠0，β ≠0，故X ≠Y，X ≠∅，Y ≠∅.令

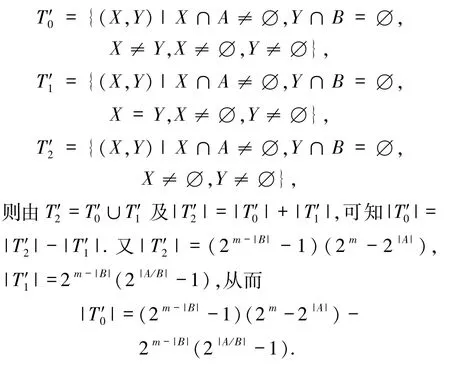
当χ（α| A）＝0，χ（β | B）＝0 时，可得X ∩A ≠∅，Y ∩B ≠∅.又α ≠β，α ≠0，β ≠0可知X ≠Y，X ≠∅，Y ≠∅.令

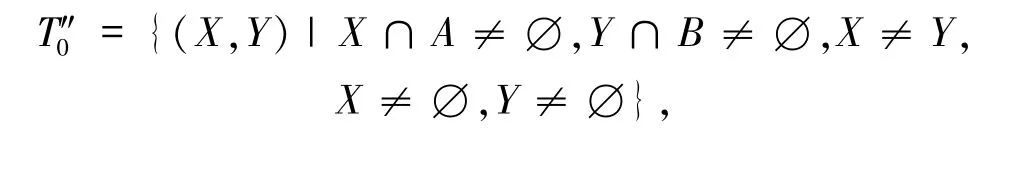
故当χ（α| A）χ（β | B）＝0 时，可得码字个数为|T0|+||+||，即

根据上述证明可知，当A ＝B时，有如下推论.

推论2.4若A ＝B，则码L2是3 权重码，其重量分布如表3 所示.

表3 码L 2（A ＝B）的重量分布Tab.3 Weight distribution of the code L 2 with A ＝B

表3 码L 2（A ＝B）的重量分布Tab.3 Weight distribution of the code L 2 with A ＝B

定理2.5若A ＝B且|A| ＝m-1，则码L2为最优二元码.

证明由定理2.3 可知，若A ＝B，|A| ＝m-1，则码L2的参数为［22m-2，2m-1，22m-3］2，从而有

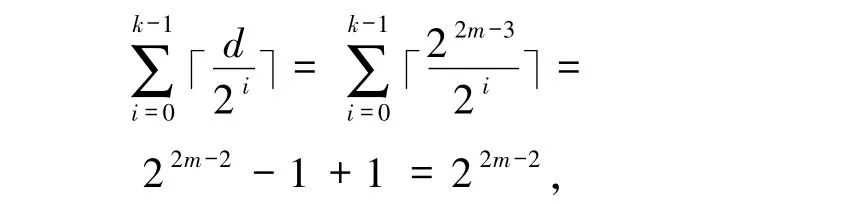
3 应用举例

下面给出2 个具体例子.

例3.1取m ＝3，ΔA＝｛（0，0，0），（0，0，1）｝，ΔB＝｛（0，0，0），（0，1，0）｝，则

进而，由定义可得

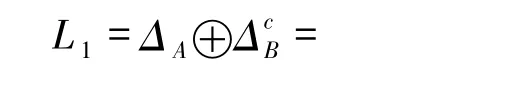
另一方面，由m ＝3，|A| ＝|B| ＝1，以及定理2.1，可知码L1的码长为12、码字个数为16，以及重量分布如表4 所示，故可得码L1的参数为［12，4，6］2，以及重量计数器为

表4 码L 1（|A| ＝|B| ＝1）的重量分布Tab.4 Weight distribution of the code L 1 with |A| ＝|B| ＝1

表4 码L 1（|A| ＝|B| ＝1）的重量分布Tab.4 Weight distribution of the code L 1 with |A| ＝|B| ＝1

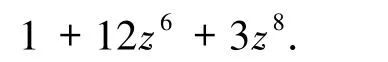
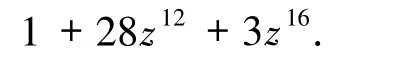
容易验证其参数［24，5，12］2满足Griesmer 界，故L1为最优二元码.

表5 码L 1的重量分布Tab.5 Weight distribution of the code L 1

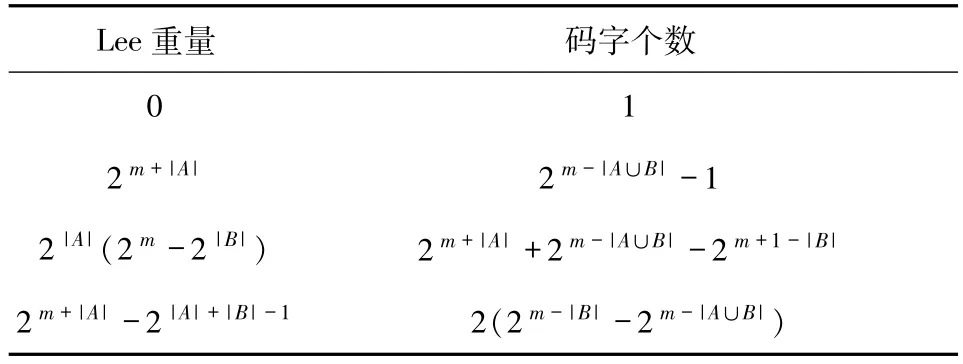
表5 码L 1的重量分布Tab.5 Weight distribution of the code L 1

表6 码L 1的重量分布Tab.6 Weight distribution of the code L 1

表6 码L 1的重量分布Tab.6 Weight distribution of the code L 1

例3.2取m ＝3，A ＝B且|A| ＝2.按照例3.1的方法，则可得码L2的全体码字，从而可以直接计算出码的参数为［16，5，8］2，以及重量计数器为

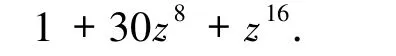
容易验证其参数［16，5，8］2满足Griesmer 界，故L2为最优二元码.

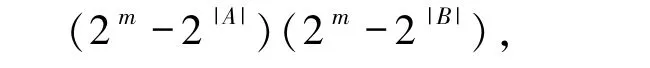
码字个数为22m，且重量分布如表7 所示.

表7 码L 2的重量分布Tab.7 Weight distribution of the code L 2

表7 码L 2的重量分布Tab.7 Weight distribution of the code L 2

码字个数为22m，且重量分布如表8 所示.

表8 码L 2的重量分布Tab.8 Weight distribution of the code L 2

表8 码L 2的重量分布Tab.8 Weight distribution of the code L 2