由正则理想确定的凝聚性研究
肖雪莲,王芳贵,林诗雨
(1.四川师范大学 数学科学学院,四川 成都 610066;2.阿坝师范学院 数学学院,四川 汶川 623002)
1 预备知识
环R称为凝聚环,如果R的每个有限生成理想I是有限表现的.凝聚环最早见于1960 年Chase[1]的研究中,并得到一个关于凝聚环的经典Chase 定理,即环R为凝聚环当且仅当平坦R-模的直积是平坦模.Stenström[2]引入FP-内射模,对凝聚环做了进一步的刻画,做出了十分漂亮的结果.由此,众多学者对凝聚环产生了浓厚的兴趣,文献[3-4]对凝聚环的性质进行了更深入的研究,而且在推广凝聚环的方面也做了很多工作.文献[4]证明了环R为凝聚环当且仅当每个内射R-模的特征模是平坦模.自然地,针对凝聚环的推广,我们将凝聚环中理想的条件弱化为正则理想,提出正则凝聚环的概念.为刻画正则凝聚环,引入正则平坦模和正则余平坦模的概念,证明正则凝聚环刻画的Chase定理(定理3.2).
Prüfer环的概念最初出现在文献[5-6]中.交换环R称为Prüfer环,是指每个有限生成正则理想是可逆理想;Prüfer环是一类典型的正则凝聚环.Griffin[6]利用乘法理想的研究方法给出了Prüfer 环多达15 条的等价刻画.由于Prüfer环的应用意义,文献[7]对Prüfer 环研究进行了系统总结.从这些结果来看,关于Prüfer 环的研究主要集中于理想刻画.为了给出Prüfer 环的模刻画,我们利用正则余平坦模与可除模的关系,给出Prüfer环的一些模理论刻画.
本文恒设R是有单位元的交换环.对R-模M,用E(M)表示M 的内射包络.如果M 是一个内射模的商模,即M≅E/X,其中E是内射模,则M称为h-可除模.用M+表示M 的特征模,即M+=HomZ(M,/).理想I 若含有非零因子,则称为正则理想.正合列ξ:0→A→B→C→0,M⊗Rξ表示
0 →M ⊗RA →M ⊗RB →M ⊗RC →0,
若M⊗Rξ仍是正合列,则称正合列ξ 是纯正合列.R-模B的子模A 称为纯子模,是指正合列0→A→B→B/A→0 是纯正合列.
2 正则余平坦模与正则平坦模
以下恒用S表示R的非零因子乘法封闭集.设M是R-模,令
T(M)={x ∈M|存在s ∈S,使得sx =0},
则T(M)是M的子模.若T(M)=0,则M称为无挠模,等价地,对任何s∈S,(M,R/(s))=0.若T(M)=M,则M 称为挠模.若对任何s∈S,都有sM =M,则M称为可除模,等价地,对任何s∈S,有(R/(s),D)=0.文献[8]称R-模D 是正则内射模,是指对任何挠模M,有(M,D)=0;文献[8]也证明了D 是正则内射模当且仅当对R 的任何正则理想I,有(R/I,D)=0.
引理2.1设D 是无挠模,则E(D)也是无挠模.
证明设s∈S,x∈E(D),sx =0,若x≠0.由于E(D)是D 的本性扩张,故存在r∈R,使得rx≠0,且rx∈D.由rsx =0,且D为无挠模,得rx =0,矛盾.故E(D)是无挠模.
引理2.2设D是无挠的可除模,则D是正则性内射模.
证明参见文献[9]定理3.4.
设R是任何交换环,用T(R)表示R 的完全商环,即T(R)=RS.于是T(R)中的元素可以表示为,其中,r∈R,s∈S.
命题2.3对任何环R,每个T(R)-模是正则内射R-模.
证明设M 是T(R)-模.对任何s∈S,则s 是T(R)的单位,从而有sM =M,即M是可除R-模.又若s∈S,x∈M,sx =0,由于s是T(R)的单位,故x =,即M还是无挠R-模.由引理2.2 可知,M是正则内射R-模.
定义2.4设E 是R-模.若对任何I∈,有(R/I,E)=0,则E称为正则余平坦模.
注2.51)正则内射模显然是正则余平坦模.当R是整环时,正则内射模就是内射模,正则余平坦模就是余平坦模.由于当R 是凝聚环时,余平坦模是FP-内射模,当R是Noether环时,FP-内射模是内射模.故当R是凝聚整环但不是Noether环时,必有一个余平坦模不是内射模.这也说明了正则余平坦模未必是正则内射模.
2)余平坦模显然是正则余平坦模,但正则余平坦模未必是余平坦模.例如,设R 是Noether 环,T(R)=R,但R不是半单环,此时余平坦模就是内射模.由于T(R)=R,则R只有一个正则理想,即R自身.从而,每个R-模都是正则余平坦模.于是,存在一个R-模是正则余平坦模,但不是余平坦模.
命题2.6对R-模E,以下各条等价:
1)E是正则余平坦模;

是正合列;
证明与余平坦模的刻画是类似的,故从略.
命题2.7正则余平坦模是可除模.
证明设E 是正则余平坦模,a∈R 是非零因子.由定义有(R/(a),E)≅E/aE =0,故有aE =E,因此E是可除模.
注2.8可除模未必是正则余平坦模.文献[11-12]证明了整环R是Prüfer整环当且仅当可除模是余平坦模.因此,只要整环R 不是Prüfer整环,则一定有一个可除模不是余平坦模.因而,也说明了可除模未必是正则余平坦模.
命题2.9设{Ei}是一簇R-模,则是正则余平坦模当且仅当每个Ei是正则余平坦模;当且仅当是正则余平坦模.
证明设I∈.由同构关系ii
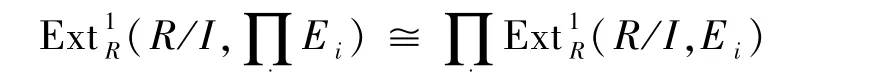
由文献[13]定理3.9.2,有自然同构
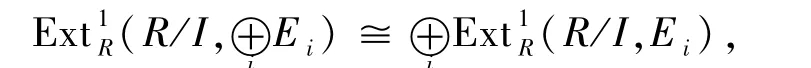
定义2.10设M是R-模.若对R 的任意正则理想I,有0→M⊗RI→M⊗RR 是正合列,等价地,(M,R/I)=0,则M称为正则平坦模.
定理2.11设R、T是环,E是内射T-模,M是R-T双模,且是正则平坦R-模,则HomT(M,E)是正则内射R-模.
证明设I 是R 的正则理想,则0 →I→R→R/I→0 是R-正合列.因为M是正则平坦R-模,故
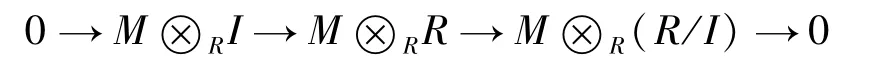
是T-正合列.由E是内射T-模,故


是T-正合列.由相伴同构定理知

是R-正合列.从而由文献[8]定 理5.3 知HomT(M,E)是正则内射R-模.
命题2.12对R-模M,以下各条等价:
1)M是正则平坦模;
5)对环R 的任何正则理想I,同态σI:I ⊗RM→IM是同构;
6)M+是正则内射R-模;
7)M+是正则余平坦R-模;
9)设ξ:0→A→B→M→0 是正合列,则对R 的任何正则理想I,R/I⊗Rξ是正合列;
10)存在正合列ξ:0→A→P→M→0,其中P为投射模,使得对R的任何正则理想I,有R/I⊗Rξ是正合列.
证明1)⇔2)⇔3)⇔4)⇔5)与平坦模的刻画是类似的,故从略.
1)⇒6)由定理2.11 知HomZ(M,/)=M+是正则内射R-模.
6)⇒7)显然.

由相伴同构定理知σI和σR同构.由M+是正则余平坦模知i*是满同态,从而(1⊗i)*是满同态.故有正合列(M⊗RR)+→(M⊗RI)+→0,可得0→M⊗RI→M⊗RR正合.

1)⇒9)设I 为R 的任意正则理想,取正合列ξ:0→A→B→M→0,可得正合列
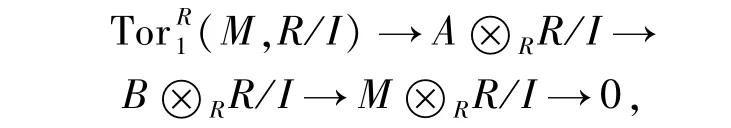
9)⇒10)显然.
10)⇒1)设I为R的任意正则理想.取正合列ξ:0→A→P→M→0,可得正合列
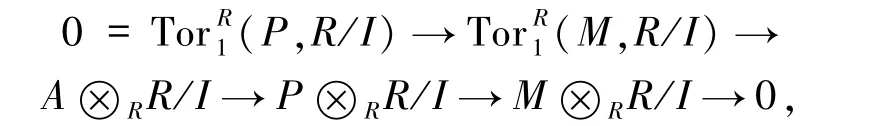
由条件R/I⊗Rξ 正合,知A⊗RR/I→P⊗RR/I 为单同态,故(M,R/I)=0.
定理2.13设R 是环,则每个R-模为正则平坦模当且仅当T(R)=R.
证明若T(R)=R,则={R},故每个R-模都是正则平坦模.
反之,设每个R-模为正则平坦模.设M 是R-模,a∈R 是正则元.由假设,M 是正则平坦模,故T(R/(a),M)≅Ma=0,其中Ma={x∈M|ax =0}.于是M 为无挠模.特别地,R/(a)是无挠模.但R/(a)为挠模,因此,有R/(a)=0,即(a)=R,故a是R的单位,从而有T(R)=R.
注2.14平坦模显然是正则平坦模.但正则平坦模未必是平坦模.例如设R是QF环,但不是半单环,则T(R)=R,且诣零根不等于零,因此,R 不是von Neumann 正则环.由于T(R)=R,则每个R-模都是正则平坦模.于是,存在一个R-模是正则平坦模,但不是平坦模.
命题2.15正则平坦模的纯子模是正则平坦模.
证明设M是正则平坦模,B 是M 的纯子模.则存在纯正合列0 →B →M→M/B →0,使得0 →(M/B)+→M+→B+→0 为分裂正合列,即M+≅(M/B)+⊕B+.由命题2.12 知,M+是正则余平坦模.由命题2.9 知,B+为正则余平坦模.又由命题2.12 知,B为正则平坦模.
命题2.16设{Mi}是一簇R-模,是正则平坦模当且仅当每个Mi是正则平坦模.
证明设I为R的任意正则理想,由文献[13]定理3.4.5 知,存在同构关系

3 正则凝聚环
回顾若环R的每个有限生成理想是有限表现的,则称R为凝聚环.下面将提出正则凝聚环的概念,并推广凝聚环的某些对应基本性质,使之对Prüfer环的模刻画发挥作用.
定义3.1环R称为正则凝聚环,是指任意I∈,I是有限表现的.
凝聚环显然是正则凝聚环.
定理3.2(正则凝聚环的Chase 定理)对环R,以下各条等价:
1)R是正则凝聚环;
2)(正则)平坦模的直积是正则平坦模;
3)R的任意直积是正则平坦模.
证明1)⇒2)设{Mi|i∈Γ}是一簇平坦模或正则平坦模,设I∈,则I 为有限表现.f、g 是对应的自然同态,则有下面的交换图.
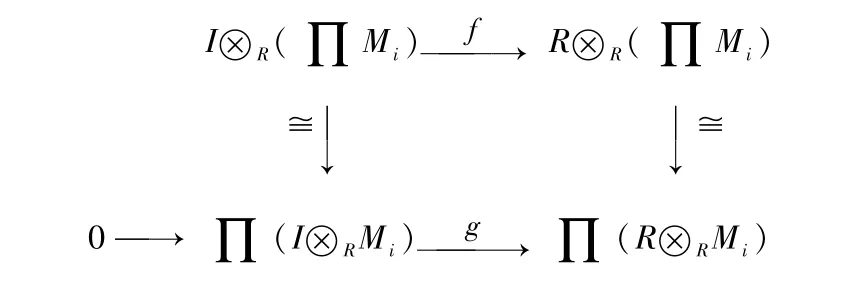
由文献[13]定理2.6.10 知,垂直的箭头是同构.又由Mi是平坦模或正则平坦模知,底行是正合列,故f是单同态,即Mi为正则平坦模.
2)⇒3)显然.
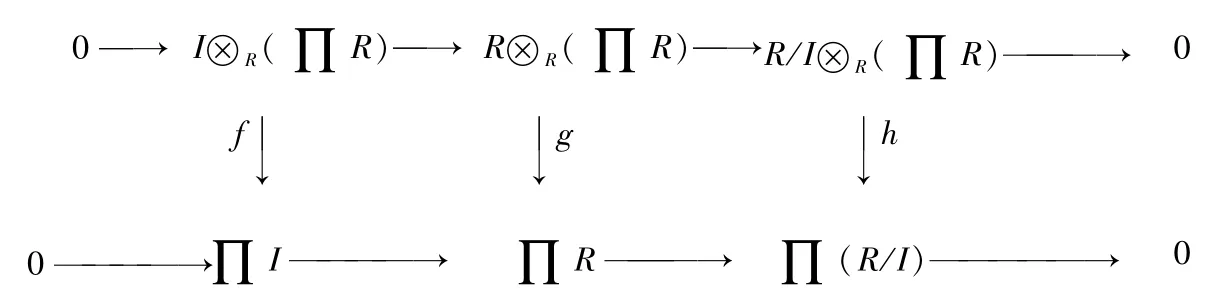
因为R/I 是有限表现模,由文献[13]定理2.6.10知,g、h同构,由五项引理知f同构.
由文献[13]定理2.6.10 知,I 为有限表现模,故R是正则凝聚环.
推论3.3若R是正则凝聚环,则Mi是正则平坦模当且仅当每个Mi是正则平坦模.
证明设Mi是正则平坦模,由定理3.2 即得Mi是正则平坦模.

命题3.4若R是正则凝聚环,则R-模M是正则余平坦模当且仅当M+是正则平坦模.
证明设M为R-模,I∈,由条件R 是正则凝聚环,知I是有限表现的.故有如下交换图.

由文献[13]定理2.6.13 知,f、g 同构.由命题2.6 知,底行正合当且仅当HomR(R,M)→HomR(I,M)→0 正合,当且仅当M 是正则余平坦模.因此,由交换图可知,M是正则余平坦模当且仅当M+是正则平坦模.
定理3.5对环R,以下各条等价:
1)R是正则凝聚环;
2)R-模M 是正则余平坦模当且仅当M++是正则余平坦模;
3)R-模M 是正则平坦模当且仅当M++是正则平坦模;
4)内射模的正向极限是正则余平坦模;
5)对任意正则余平坦R-模M,及内射R-模N,同态模HomR(M,N)是正则平坦模;
6)对任意内射R-模N,同态模HomR(R+,N)是正则平坦模.
证明1)⇒2)由命题3.4 知,M 是正则余平坦模当且仅当M+是正则平坦模.又由命题2.12知,则M+是正则平坦模当且仅当M++是正则余平坦模.
2)⇒3)M是正则平坦模,则M+是正则余平坦模.由条件知,M+++是正则余平坦模.由命题2.12知,M+++是正则余平坦模当且仅当M++是正则平坦模.

1)⇒4)设环R是正则凝聚环,Γ是定向集,Mi(i∈Γ)是内射模的正向系.对任意I∈,I 为有限表现的,由文献[18]知


由文献[13]定理3.9.4 知,f、g同构,由五项引理知h同构.由文献[16]知,I 为有限表现,故R 是正则凝聚环.
1)⇒5)对任意正则余平坦R-模M,及内射R-模N,既然/是内射上生成子,则存在正合列0 →N →(/).因为N 为内射模,则存在某一R-模B,使得(/)≅N ⊕B.故有
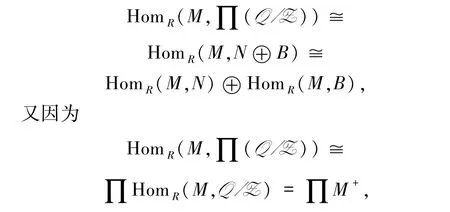
则HomR(M,N)是M+的直和加项.由条件知R是正则凝聚环,故由命题3.4 及定理3.2 知,M+是正则平坦模.又由命题2.16 知,HomR(M,N)是正则平坦模.
5)⇒6)由R+是内射模,即证.
6)⇒1)由
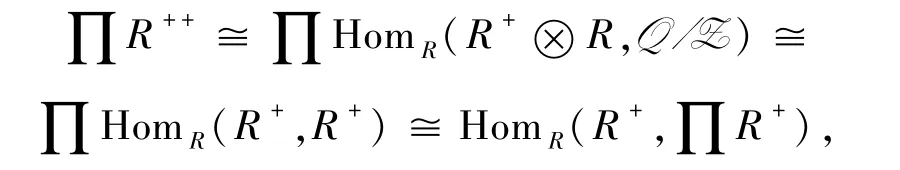
引理3.6[19]1)设M是R-模,则M是平坦模当且仅当M+是FP-内射模;
2)设B 是R-模,B+是平坦模,则B 是FP-内射模.
定理3.7设环R 是正则凝聚环,以下各条等价:
1)任意正则平坦R-模是平坦模;
2)任意正则余平坦R-模是FP-内射模;
3)任意正则余平坦模且为纯内射R-模是内射模.
证明1)⇒2)设B 为正则余平坦R-模,则B+为正则平坦模,由条件得,B+为平坦模,由引理3.6 知,B是FP-内射模.
2)⇒3)显然.
3)⇒1)设M 为正则平坦R-模,由命题2.12知,纯内射R-模M+为正则余平坦模.故由条件可知M+为内射模,因此,M为平坦模.
设I是R的有限生成正则理想,但并不意味着每个生成元都是非零因子.为了给出下面的Prüfer环的刻画,需要对可除模作更一般的刻画.设N 是R-模,称{Nα|α≤π}是N的子模的连续升链,是指N有子模升链

其中π和每个α都是序数,指标集是连续序数的集合,且当α是极限序数时,Nα=∪β<αNβ.
引理3.8设N是挠模,则N有子模的连续升链(1),使得对每个序数α,Nα+1/Nα是循环挠模.
证明令N0=0.若N =0,取π=0.设N≠0,取x∈N,x≠0,则令N1=Rx.对给定的序数α,设β <α时,满足要求的Nβ已经作出.若有Nβ=N,则做法停止.否则,当α 不是极限序数时,取x∈N -Nα-1,并令Nα=Nα-1+Rx.于是Nα/Nα-1是循环挠模.当α是极限序数时,令Nα=∪β<αNβ.如此下去,即得所证.
命题3.9对R-模D,以下各条等价:
1)D是可除模;
4)对任何循环挠模N,D⊗RN =0;
5)对任何挠模N,D⊗RN =0.
证明1)⇒2)对任何I∈,则I 中存在一个非零因子s.由于D 是可除模,故有sD =D,从而有ID =D.故D是-可除模.
2)⇔3)这是显然的.
3)⇒4)由于N 是循环模,故可设N =R/I,其中I是R 的理想.由于N 是循环挠模,故存在正则元素a∈I.于是有正合列

从而得到D⊗RN =0.
4)⇒5)由引理3.8,N 有连续升链(1).由于N1与N2/N1是循环挠模,故由正合列
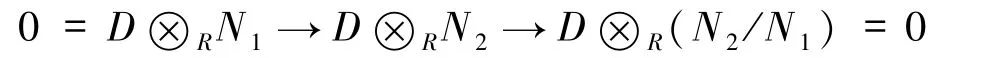
得到D⊗RN2=0.用超限归纳法可证对任何序数α≤π,都有D⊗RNα=0.特别地,有
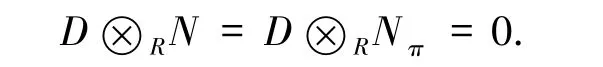
设A是T(R)中的R-子模,定义
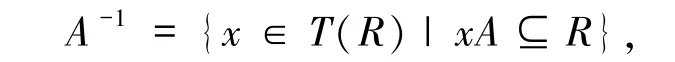
则A-1是T(R)中的R-子模.若有AA-1=R,则称A是可逆模.R 的理想若是可逆模,则称之为可逆理想.
引理3.10[9]设A 是T(R)中的R-子模.则有:
1)若A是可逆的,则A是有限生成的;
2)若A包含T(R)中的一个单位,则A是投射模当且仅当A是可逆的;
3)有限生成的正则平坦理想是投射模.
证明1)和2)的证明参见文献[9]引理5.3.
3)由文献[20]引理18.1 即得.
命题3.11Prüfer环是正则凝聚环.
证明设I是R 的有限生成正则理想,则I 是可逆的.由引理3.10 的2)知,I为投射模,从而I为有限表现的.故R是正则凝聚环.
定理3.12对环R,以下各条等价:
1)R是Prüfer环;
2)可除模是正则余平坦模;
3)正则余平坦模的商模是正则余平坦模;
4)正则内射模的商模是正则余平坦模;
5)h-可除模是正则余平坦模;
6)R的正则理想是平坦模;
7)设M 是有限生成自由模F 的有限生成子模,且F/M是挠模,则M是投射模.
证明1)⇒2)设D是可除模,I =(a1,a2,…,ak)是R的有限生成正则理想,f:I→D是同态.由于R是Prüfer 环,故II-1=R.于是有x1,x2,…,xn∈I-1,使得.由命题3.9 知,D是-可除模,从而有ID =D,故存在yij∈D,使得

由于xi∈I-1,aj∈I,故对任何i,j,有xiaj∈R.于是

对任何b∈I,有

令g:R→D,使得g(r)=ry,r∈R.则对任何b∈I,有g(b)=bg(1)=by =f(b).由命题2.6,D 是正则余平坦模.
2)⇒3)由命题2.7,正则余平坦模是可除模.又可除模的商模还是可除模,从而正则余平坦模的商模是正则余平坦模.
3)⇒4)由正则内射模是正则余平坦模即知.4)⇒5)内射模显然是正则内射模,由h-可除模的定义知h-可除模为正则余平坦模.
5)⇒1)设I是R的有限生成正则理想,X为任意R-模.嵌入X 到内射模E,则有正合列0→X→E→E/X→0.于是E/X是h-可除模.于是有
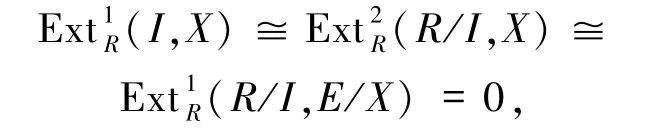
故I是投射模.由引理3.10 知I 是可逆的,因此,R是Prüfer环.
1)⇒6)设A 是R 的正则理想,则存在非零因子a∈A.显然有A 的包含a 的有限生成子理想的集合是定向集,且A =∪B,其中B 取遍A 的包含a的有限生成子理想.由假设,每个B是投射模,从而有A是平坦模.
6)⇒1)由引理3.10 的3)即得.
1)⇒7)记F =Rn,对n用归纳法证明之.
n =1 时,则M是R的理想.由于R/M是挠模,故M是R 的有限生成正则理想.由于R 是Prüfer环,故M是投射模.
今设n >1,令F1=Rn-1,N =M ∩F1.于是F/F1≅R,且有下面的两行是正合列的交换图.

其中,Y =F/M是挠模,h是左边交换方图的诱导同态.由文献[21]引理1,h 是单同态.由蛇形引理,0→M/N→R→cok(h)→0 是正合列.由于cok(h)=Y/h(X)是挠模,故M/N 是投射模,从而有M 是投射模.
7)⇒1)由引理3.10 即得.

