方程Z（SL（n））＝φe（n）（e＝3，4，6）的正整数解

杜 珊，廖群英，王慧莉

（四川师范大学 数学科学学院，四川 成都 610066）

1 序言及主要结果

数论函数是数论研究中的一个重要课题，也是研究数论问题不可或缺的工具.18 世纪，欧拉首次提出了欧拉函数的概念：正整数n 的欧拉函数φ（n）定义为序列1，2，…，n中与n互素的正整数的个数［1］.该函数在RSA 公钥密码体制建立中扮演着重要角色［2］.2002 年，为了将Lehmer 同余式的模从素数平方推广到任意整数的平方，Cai［3］定义了正整数n的广义欧拉函数：对给定正整数e，正整数n的广义欧拉函数φe（n）为序列中与n互素的数的个数，易证

其中μ（n）为n的麦比乌斯函数.显然，当e ＝1 时，φ1（n）＝φ（n），即著名的欧拉函数；特别地，e|φ（n）时，有.目前为止，已经得到e ＝3，4，6 的准确计算公式和e ＝5 的部分计算公式［5-7］，以及某些特殊的e，φe（n）的计算公式［8-9］.

对于任意正整数n，数学家Smarandache定义n的Smarandache函数S（n）为满足n|m！的最小正整数n，并提出了很多有趣的数论问题［10］.伪Smarandache函数Z（n）定义为最小的正整数m，使得1 +2 +…+m能被n整除［11］，即

而Smarandache LCM函数SL（n）则定义为最小的正整数m，使得1，2，…，m 的最小公倍数能被n 整除［12］，即

2005 年之后，许多学者研究了关于Smarandache LCM函数、伪Smarandache 函数和广义Euler函数相关性质及方程问题，并取得了一些好的结果［13-16］.同时，也有很多学者研究了相关的复合方程问题，例如：朱杰等［17-18］研究了方程Z（n）＝φe（SL（n））的可解性，并给出了全部的正整数解；杨张媛等［19］给出了方程Z（SL（n））＝（n）（e ＝1，2）的所有正整数解；基于欧拉函数是积性函数和相关函数的基本性质，张利霞等［20-22］给出了方程S（SL（n））＝φe（n）和Z（SL（n））＝φe（n）（e ＝1，2）的所有正整数解.但是当e ＞2 时，φe（n）不是积性函数，故文献［22］提出如下猜想.

猜想方程Z（SL（n））＝φ3（n）有可数个解.

本文证明了上述猜想，进而利用e ＝4，6 时广义欧拉函数φe（n）的准确计算公式，讨论了数论函数方程

的可解性，即证明了如下主要结果.

定理1.1若e ＝3，则方程（1）的解为n ＝45，72，90.

定理1.2若e ＝4，则方程（1）的解为n ＝5p，10p，8p1，12p2，其中，p、p1、p2为奇素数且p ≥7，p1≥11，p2≥5.

定理1.3若e ＝6，则方程（1）的解为n ＝7p，14p，其中p ＞7 为奇素数.

2 相关引理

为后文叙述方便，设n、s为正整数，记Ω（n）为n的素因子个数（重复计数），ω（n）为n 的不同的素因子个数，并规定Ω（1）＝ω（1）＝0.为证明本文的主要结果，需要如下几个引理.

引理2.1［23］设正整数n的标准分解式为n ＝，则

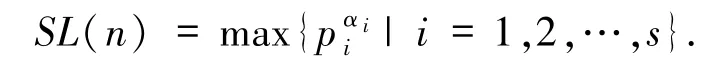
特别地，当p为素数且α≥1 时，SL（pα）＝pα.

引理2.2［24］对任意素数p ≥3 及α ∈N，Z（pα）＝pα-1；当p ＝2 时，Z（2α）＝2α+1-1.

引理2.3［6］若，其中α，αi≥0，pi是不同的素数，且gcd（pi，3）＝1（i ＝1，2，…，s），则

引理2.6［21］1）若n ＝3α，α ＞1，则；

2）若n ＝2α，α ＞2，则φ4（n）＝；

3）若n ＝2α3β＞6，则

3 主要结果的证明

定理1.1 的证明当e ＝3 时，方程（1）即为Z（SL（n））＝φ3（n）.显然，n ＝1，2，3 不是方程的解.

现设n ＞3.若n ＝3α（α ＞1），则由引理2.1～2.2 可知Z（SL（n））＝Z（3α）＝3α-1.再由引理2.6可知φ3（3α）＝2 ×3α-2，此时方程（1）即为3α-1 ＝2 ×3α-2，显然无解.故不妨设，其中，p1、…、ps为互不相同的素数，且s≥1，α≥0，α1，…，αs≥1.

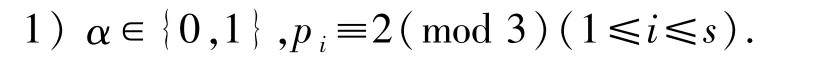
若3α＝max｛3α，|i ＝1，2，…，s｝，又α∈｛0，1｝，故n ＝6.此时由引理2.1～2.2可知Z（SL（6））＝Z（3）＝2，又φ3（6）＝1，显然此时方程无解.

对比等式两边的奇偶性可知s ＝1，即

又α∈｛0，1｝，则

矛盾.故ps为奇素数，且ps≡5（mod 6），则由引理2.2可知Z（SL（n））＝Z（）＝-1，再由引理2.3，方程（1）即为

对比等式两边的奇偶性可知s≥2.若s ＝2，由（2）式可得

则（ps-1）|2，与ps≡5（mod 6）矛盾，故s≥3.由（2）式得

由s≥3 且pi≡2（mod 3）（1≤i≤s），故至少存在s-1 个pi满足pi≥5（1≤i≤s），不妨设ps-1≥5.则

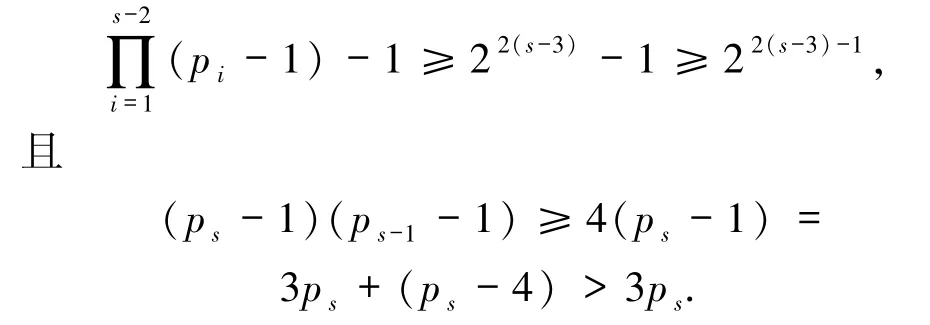
由（3）式可得

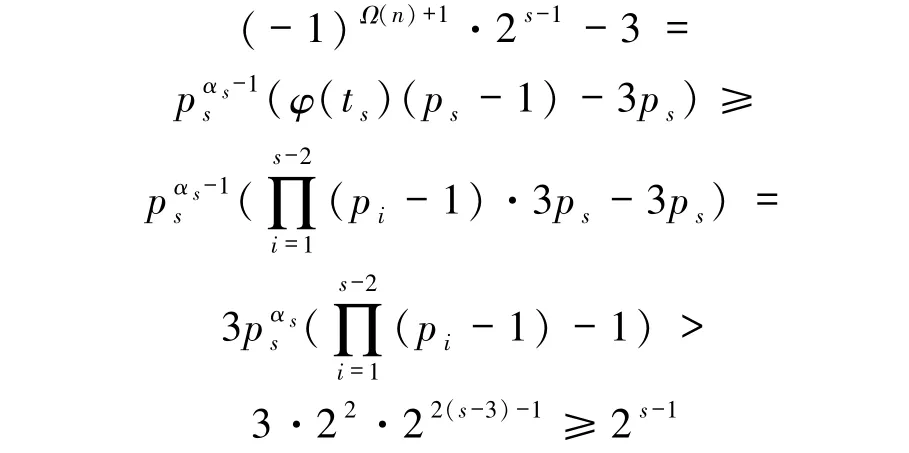
矛盾，即此时方程无解.

2）α≥2 或α∈｛0，1｝且存在pi≡1（mod 3）（1≤i≤s）.

故此时方程（1）为2·3α-2φ（t）＝3α-1.考虑等式两边3 的个数可知α ＝2，从而φ（t）＝4，即t ＝5，8，10，12.又gcd（t，3）＝1，故t ＝5，8，10，相应的n ＝45，72，90，经检验均为方程的解.

故方程（1）为

对比等式两边的奇偶性可知矛盾.故ps为奇素数，由引理2.2 知

对比等式两边ps的个数可知αs＝1，即

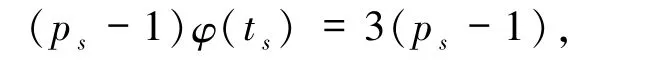
从而φ（ts）＝3，矛盾.

综上，定理1.1 得证.

定理1.2 的证明当e ＝4 时，方程（1）即为Z（SL（n））＝φ4（n）.显然，n ＝1，2，3，4 不是方程的解.

现设n ＞4.若n ＝2α（α≥3），则由引理2.1～2.2 可知

则（ps-1）|2s，又ps≡3（mod 4），故ps＝3.若s ＝1，则φ（ts）＝φ（2α）＝1，再由（4）式可得

矛盾.故s≥2，又ps＝3 且pi≡3（mod 4）（i ＝1，2，…，s），故pi≥7（1≤i≤s-1），则

再由（4）式可得

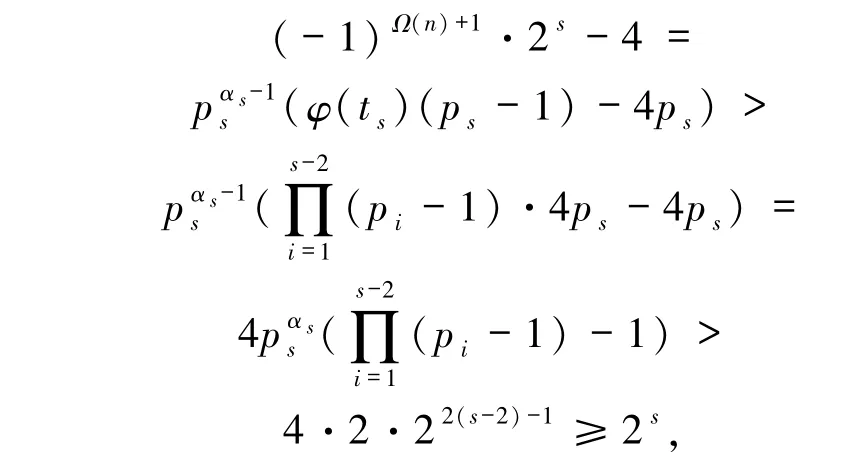
矛盾，即此时方程无解.

2）α≥2 或α∈｛0，1｝且存在pi≡1（mod 4）（1≤i≤s）.

若2α＞max，…，s｝，则α≥3，由引理2.1～2.2 可得

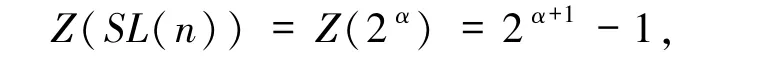
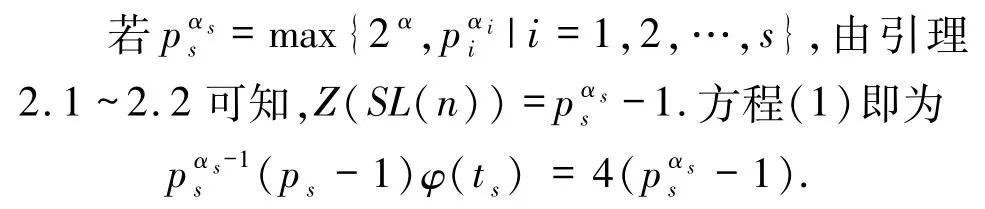
对比等式两边ps的个数可知αs＝1，即

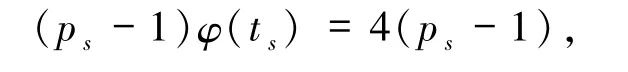
则φ（ts）＝4，从而ts＝5，8，10，12，相应的n ＝5p，10p（p ＞5），8p1（p1≥11），12p2（p2≥5），其中p、p1、p2均为素数.经检验均为方程的解.

综上，定理1.2 得证.

定理1.3 的证明当e ＝6 时，方程（1）即为Z（SL（n））＝φ6（n），显然，n ＝1，2，3，4，5，6 均不是解.

设n ＝2α3β＞6（α，β≥0）.若β ＝0，则α≥3，由引理2.1～2.2，Z（SL（n））＝2α+1-1，再由引理2.6，

故矛盾；若β ＝1，则α ≥3，由引理2.1～2.2，Z（SL（n））＝2α+1-1，再由引理2.6，

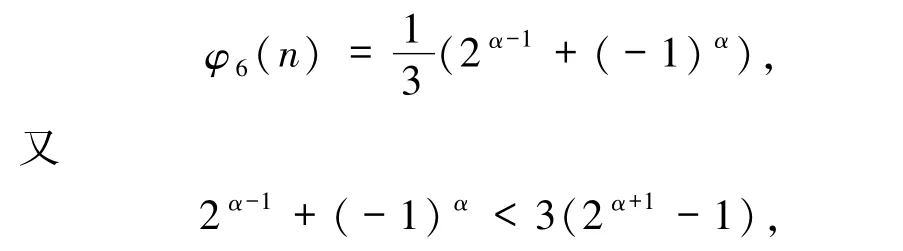
矛盾；若β≥2，由引理2.6，

若2α＞3β，则α≥4，由引理2.1～2.2，Z（SL（n））＝2α+1-1，方程（1）为

等式两边奇偶性不同，矛盾.若3β＞2α，则由引理2.1～2.2，

方程（1）为

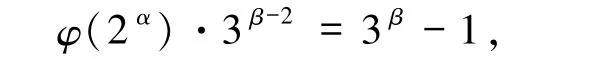
对比等式两边3 的个数，可知β ＝2，从而φ（2α）＝8，即α ＝4，与3β＞2α矛盾，故此时方程无解.不妨设

其中，p1、…、ps为互不相同的素数，且s≥1，α≥0，α1，…，αs≥1.令，则gcd（ts，ps）＝1，有以下4 种情况.

若s ＝1，则φ（ts）＝φ（3β）≤2，再由（6）式，

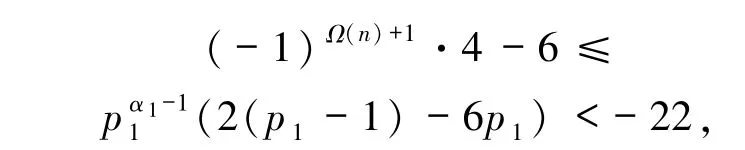
矛盾；若s ＝2，由（5）式可得

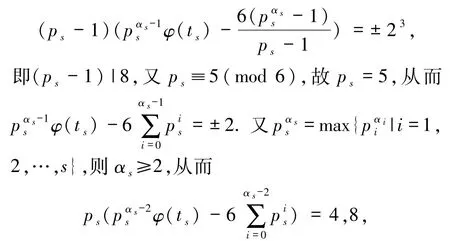
又ps＝5，故矛盾.若s≥3，则至少存在s-1 个pi满足pi≥11（1≤i≤s），此时pi-1 ＞23.不妨设ps-1≥11，从而

再由（6）式可知

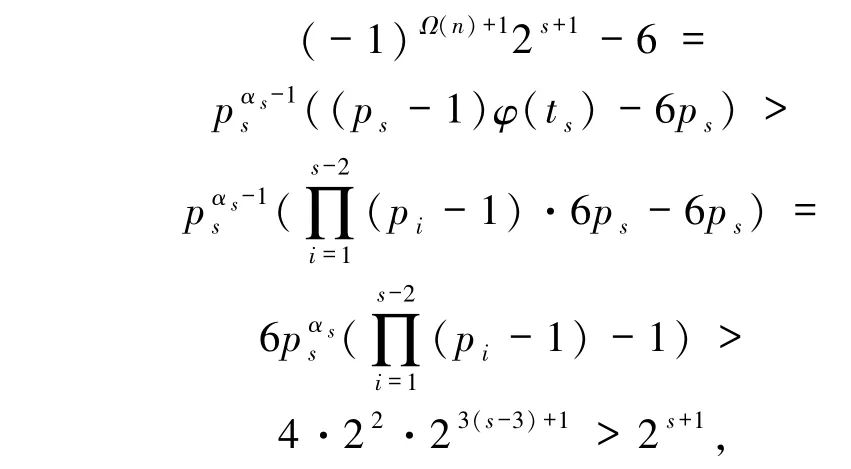
矛盾，故此时方程无解.

2）α ＝1，β∈｛0，1｝且pi≡5（mod 6）（i ＝1，2，…，s）.

故（ps-1）|2s，又ps≡5（mod 6），则s≥2.若s ＝2，则ps＝5 且p1≥11，从而φ（ts）＝φ（3β·）≥10.由（7）式可得

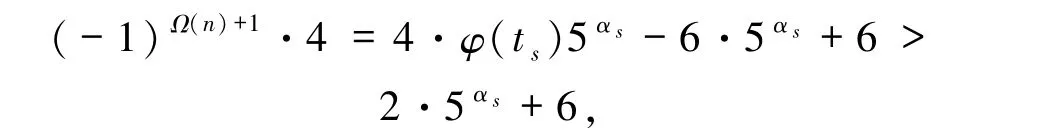
矛盾.对s≥3，由（7）式及类似定理1.3 的1）的证明可得

矛盾，故此时方程无解.

3）α≥2，β∈｛0，1｝且pi≡5（mod 6）（i ＝1，2，…，s）.

对比等式两边2 的个数，可知矛盾.

矛盾，故此时方程无解.

4）β≥2，或β∈｛0，1｝且存在pi≡1（mod 6）（1≤i≤s）.

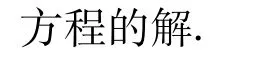
综上，定理1.3 得证.