含有2个不同素因子的k-盈不完全数

王爱钧，廖群英

（四川师范大学 数学科学学院，四川 成都 610066）

1 序言及主要结果

σ（n）是正整数n的全部正因数之和.当σ（n）＝2n时，称n 为perfect 数（完全数）［1-8］.2012 年，Pollack等［9］基于偶完全数的判别条件，给出了nearperfect数（盈完全数）的概念：若D1＝｛d1：d1|n，1≤d1≤n｝，则存在d∈D1-｛n｝，使得σ（n）＝2n +d，此时称n为盈完全数且d 为冗余因子.2013 年，Ren等［10］确定了含有2 个不同素因子的全部盈完全数.Tang等［11］证明了不存在含有3 个不同素因子的奇盈完全数.2016 年，Tang等［12］证明了含有4个不同素因子的奇盈完全数有且仅有一个，即为34·72·112·192.与函数σ 的定义类似，设p 为质数，α 为正整数，对于每个素数方幂pα，Iannucci［13］定义了一个可乘函数

并规定ρ（1）＝1.2013 年，Toth［14］指出函数ρ 具有双重性质.Wei 等［15］以及McCarthy［16］对ρ 进行了相关的研究.若kρ（n）＝n（k∈Z+），则n 被称作kimperfect数（k-不完全数）；进而，对一个冗余因子d，称满足kρ（n）＝n +d 的n 为k-near-imperfect 数（k-盈不完全数）.特别地，k ＝2 时，则简称为imperfect数（不完全数）以及near-imperfect 数（盈不完全数）.本文研究方程

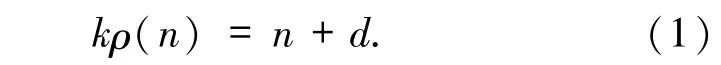
对于n只含有2 个不同素因子的情况下，给出方程（1）的全部解.假设），冗余因子，其中，p1＜p2，0≤γ1≤α1，0≤γ2≤α2且γ1+γ2＜α1+α2.由（1）式可得

定理1.1若k ＝3，则（1）式的全部解为

引理1.2若k ＝4，则（1）式仅有解（n，d）＝（2·3，2）.

2 主要结果的证明

为证明主要结果，需要以下引理.

引理2.1（卡塔兰猜想）［17］不定方程xa-yb＝1 仅有一组大于1 的正整数解

定理1.1 的证明当k ＝3 时，由p1≥3 及（2）式的推导形式可得

矛盾，故p1＝2，相应的，其中p2为奇质数．现分如下4 种情况．

若γ2＝0，则（4）式即为

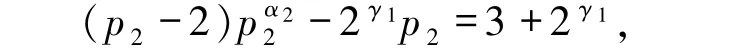
故p2|3 +2γ1.由γ1≤α1＝1，可知γ1＝0 或1.当γ1＝0时，得p2|4，此与p2为奇质数相矛盾；当γ1＝1 时，得p2|5.由p2为奇质数，故p2＝5，即（4）式为3· 5α2＝15，得α2＝1，即n ＝2·5 且d ＝2.经验证其为（2）式的解.

若γ2≠0，此时由（4）式可知p2|3，故p2＝3.从而3γ2（3α2-γ2-3·2γ1-2γ1）＝3，故γ2＝1，即3α2-1-2γ1+2＝1.由引理2.1 可知γ1＝1，α2＝3，即n ＝2·33且d ＝2·3.经验证其为（2）式的解.

2）若α1≥3，则（3）式两边同时除以可得

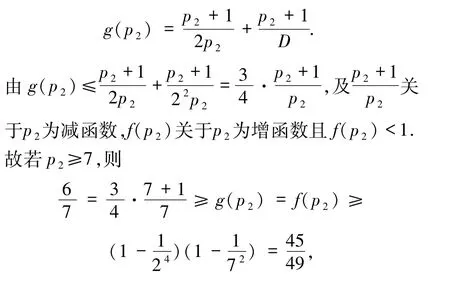
矛盾.从而p2≤5，又p2为奇质数，则p2＝3 或5.故

若p2＝3，则g（3）＝.由（5）式可知D≥2·32，此时

由α1≥3，得α2＝1.于是由（3）式可得

故γ1＝1，则由（6）式可得2α1-1-3γ2＝1.故由引理2.1 可知，当γ2＝0 时，得α1＝2，与2α1矛盾；当γ2＝1 时，得α1＝3，即n ＝23·3 且d ＝2·3.经验证其为（2）式的解.

由α1≥3，得α2＝1 且α1＝3.于是由（3）式可得2γ15γ2＝20，故γ1＝2 且γ2＝1，即n ＝23·5 且d ＝22·5.经验证其为（2）式的解.

情形2当2α1且2|α2时，由（2）式可得

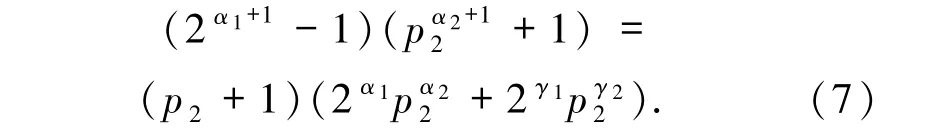
1）若α1＝1，则由（7）式可得

若γ2＝0，则（8）式即为

故p2|3 -2γ1.由γ1≤α1＝1，可知γ1＝0 或1.当γ1＝0时，得p2|2，此与p2为奇质数相矛盾；当γ1＝1 时，得p2|1，此与p2为奇质数相矛盾.

若γ2≠0，此时由（8）式可知p2|3，故p2＝3.从而3γ2（2γ1+3·2γ1-3α2-γ2）＝3，故γ2＝1，即2γ1+2-3α2-1＝1.由引理2.1 可知γ1＝0，α2＝2，即n ＝2·32且d ＝3.经验证其为（2）式的解.

2）若α1≥3，则（7）式两边同时除以可得

矛盾.从而p2≤3，又p2为奇质数，则p2＝3.由（9）式得

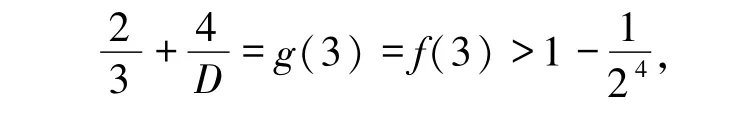
得D ＝22·3.故α1＝γ1+1 且α2＝γ2，则由（9）式可得

即2α1+1-3α2+1＝1.由引理2.1 可知，α2＝0 且α1＝1，与α1≥3 矛盾.

情形3当2|α1且2|α2时，由（2）式可得

矛盾.从而p2≤3，又p2为奇质数，故p2＝3.若2α1-γ13α2-γ2≥3，则由（11）式得

矛盾.故2α1-γ13α2-γ2≤2，即α1-γ1＝1 且α2-γ2＝0，则由（10）式可知

情形4当2|α1且2α2时，由（2）式可得

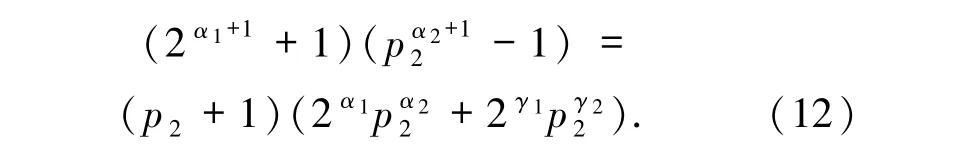
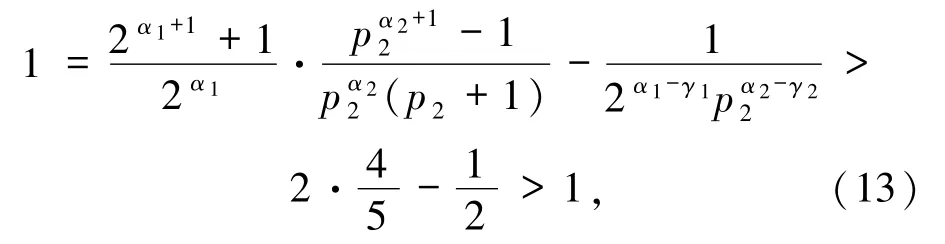
矛盾.从而p2≤3，又p2为奇质数，故p2＝3.若2α1-γ13α2-γ2≥4，则由（13）式得

矛盾.故2α1-γ13α2-γ2≤3，即α1-γ1＝1 且α2-γ2＝0，或者α1-γ1＝0 且α2-γ2＝1.

若α1-γ1＝1 且α2-γ2＝0，则由（12）式可知（2α1+1+1）（3α2+1-1）＝4（2α13α2+2α1-13α2），即3α2+1-2α1+1＝1，由引理2.1 可知α2＝1 且α1＝2，即n ＝22·3 且d ＝2·3.经验证其为（2）式的解.

若α1-γ1＝0 且α2-γ2＝1，则由（12）式可知（2α1+1+1）（3α2+1-1）＝4（2α13α2+2α13α2-1），即2α1+1（3α2-1-1）+（3α2+1-1）＝0，矛盾.

综上可知，定理1.1 得证.

定理1.2 的证明当k ＝4 时，由p1≥3 及（2）式的推导形式可得

矛盾，故p1＝2，相应的，其中p2为奇质数.现分如下4 种情况.

情形1当2α1且2α2时，由（2）式可得

1）若α1＝1，则由（14）式可得

若γ2＝0，则（15）式即为

故p2|4 +2γ1.由γ1≤α1＝1，可知γ1＝0 或1.当γ1＝0时，得p2|5，由p2为奇质数，故p2＝5，即（15）式为8·5α2＝10，矛盾.当γ1＝1 时，得p2|6，由p2为奇质数，故p2＝3，即（15）式为3α2＝3，则α2＝1，即n ＝2·3 且d ＝2.经验证其为（2）式的解.

若γ2≠0，此时由（15）式可知p2|4，此与p2为奇质数相矛盾.

2）若α1≥3，则（14）式两边同时除以可得

矛盾.

情形2当2α1且2|α2时，由（2）式可得

1）若α1＝1，则由（16）式可得

若γ2＝0，则上式即为2γ1p2-（2p2-2）＝4 -2γ1，故p2|4 -2γ1.由γ1≤α1＝1，可知γ1＝0 或1.当γ1＝0 时，得p2|3，由p2为奇质数，故p2＝3.即（17）式为4·3α2＝0，矛盾；当γ1＝1 时，得p2|2，此与p2为奇质数相矛盾.

若γ2≠0，此时由（17）式可知p2|4，此与p2为奇质数相矛盾.

2）若α1≥3，则（16）式两边同时除以可得

矛盾.

情形3当2|α1且2|α2时，由（2）式可知

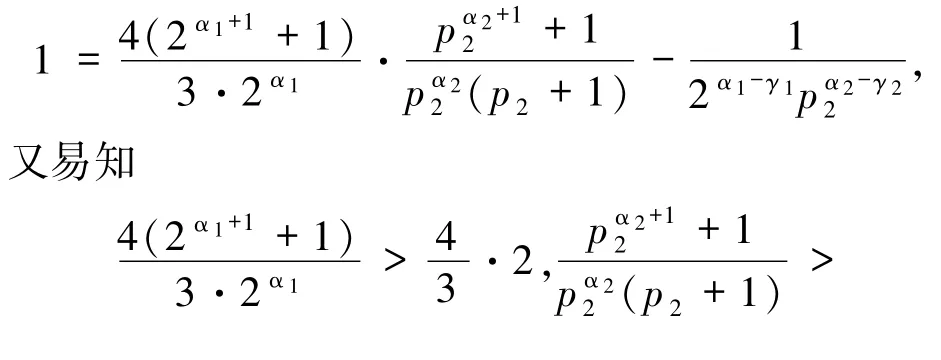
情形4当2|α1且2α2时，由（2）式可知

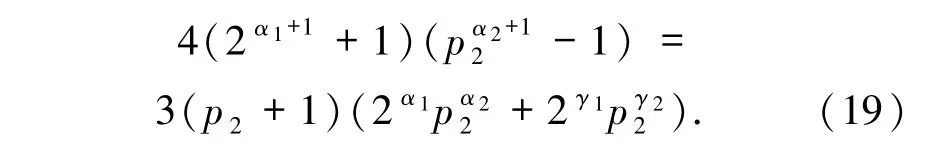
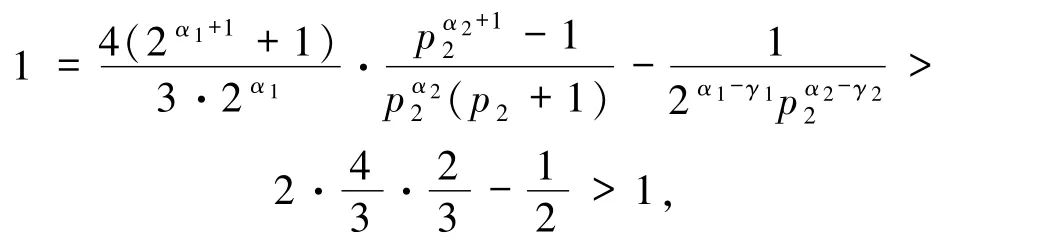
矛盾.

综上可知，定理1.2 得证.