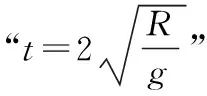巧用等时圆结论解答物理题
山东 张岩松 杨文成
一、等时圆模型
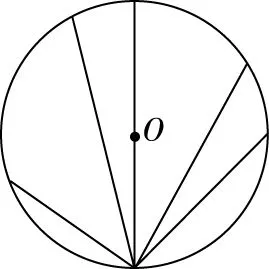
图1

图2
证明1
在图1中任意选取一根直杆bd,并假定直杆bd与辅助线ab的夹角为α,过d点做圆的切线,则直杆bd与切线的夹角也为α,如图3所示。
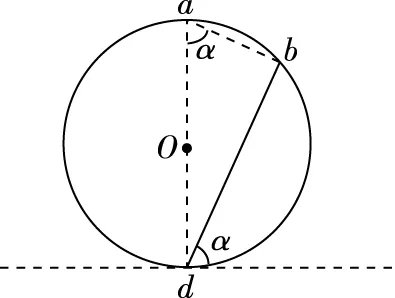
图3
由图3可知bd=2Rsinα。
当小滑环从b点滑向d点时有
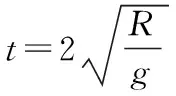
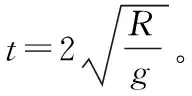
证明2
在图2中任意选取一根直杆AC,连接BC,假设AB与BC的夹角为θ,从C点做直径AB的垂线,设垂足为D点。如图4所示。由图4可知∠ACD=θ。

图4
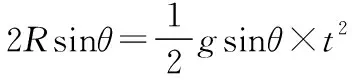
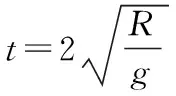
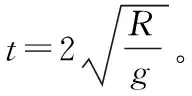
二、等时圆典型例题讲解:
【例1】如图5所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环轨道的圆心。已知在同一时刻,a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点;c球由C点自由下落到M点;则
( )
A.a球最先到达M点
B.b球最先到达M点
C.c球最先到达M点
D.b球和c球都可能最先到达M点
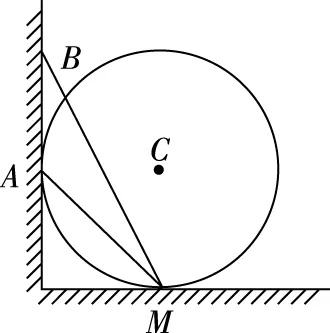
图5
【解析】由等时圆结论不难看出:ta等于等时圆时间,
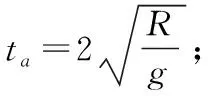
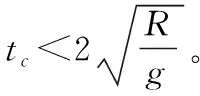
故应选C。
【例2】如图6所示,两个圆1和2外切,它们的圆心在同一竖直直线上,有三块光滑的板,它们的一端搭在墙上,另一端搭在圆2的圆周上,三块板都通过两圆的切点,A在圆周上,B在圆内,C在圆外,从A、B、C三处同时由静止释放一个小球,它们都沿板运动,则最先到达圆2的圆周上的球是
( )
A.从A处释放的球 B.从B处释放的球
C.从C处释放的球 D.同时到达
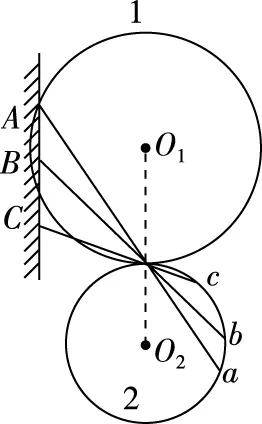
图6
【解析】根据“等时圆结论”,因为A点在圆周上,B点在圆周的里面,而C点在圆周的外面,所以从B处释放的球最先到达圆2的圆周上,从C处释放的球最后到达圆2的圆周上。故选B。
【例3】如图7所示,ab、ac是竖直平面内两根固定的光滑细杆,a、b、c位于同一圆周上,O为该圆的圆心,ab经过圆心。每根杆上都套着一个小滑环,两个滑环分别从b、c点无初速度释放,用v1、v2分别表示滑环到达a点的速度大小,用t1、t2分别表示滑环到达a点所用的时间,则
( )
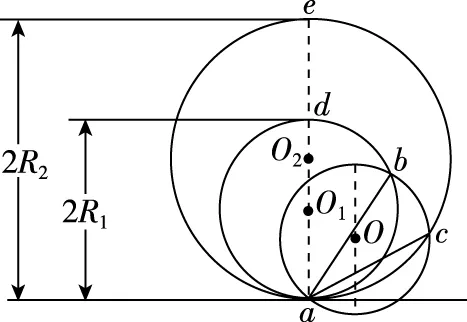
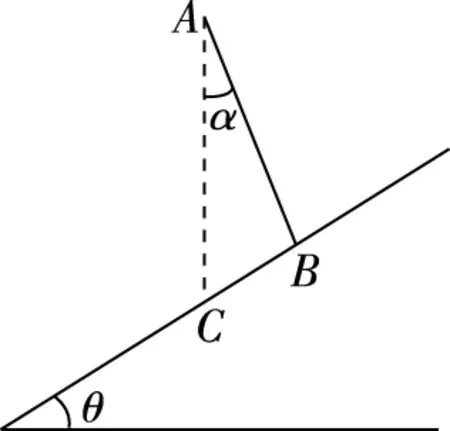
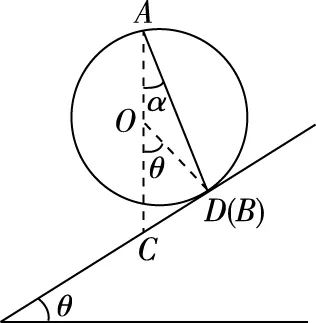
A.v1>v2B.v1 图7 因为b环下降的竖直高度比c环下降的竖直高度高,故:v1>v2,所以A正确; 从a点做竖直向上的辅助线ae,该直线与原来的过O点的竖直直径平行。 过a、b两点做辅助圆,使其圆心O1在直线ae上,如图8所示,设其半径为R1。 同理,过a、c两点做辅助圆,使其圆心O2在直线ae上,如图8所示,设其半径为R2。 因为R2>R1,所以t2>t1,故D正确。 综上所述,答案应选AD。 图8 【例4】如图9所示,在倾角为θ的斜面上方的A点处放置一光滑的木板AB,B端刚好搭在斜面上。木板与竖直方向AC所成角度为α,一小物块自A端沿木板由静止滑下,要使物块滑到斜面的时间最短,则α与θ角的大小关系应为 ( ) 图9 图10 高中物理中有许许多多的物理模型,譬如追击相遇模型、晾衣架模型、板块模型、传送带模型、突变非突变模型、定杆动杆模型、人船模型、活塞气缸模型、液柱玻璃管模型等等。 通过建模,推导出一些结论,然后利用这些结论去解题,这是我们解题常用的方法。实际上在高中物理中还有着许许多多的这样结论,它们是由物理基本规律和基本公式推导出来的。这些结论其实并不是真正的物理公式,但是利用这些结论去解题能够省时省力,可以提高解题的效率和解题的准确率,我们平时解题时一定要注意积累。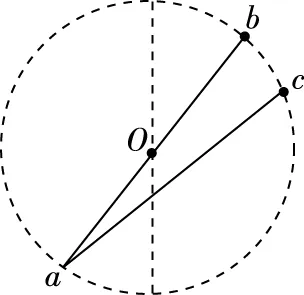
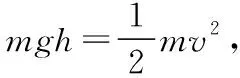

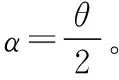
结语