面齿轮磨削齿面力热耦合及残余应力研究

李 湾 刘海渔

谭立志1 明 瑞2

肖 磊2 明兴祖2

1.湖南汽车工程职业学院

机电工程学院

湖南 株洲 412000

2.湖南工业大学

机械工程学院

湖南 株洲 412007

0 引言

面齿轮是应用于包装机械、交通及航空等领域中传动机构的新型零件，具有承载能力强、传动噪声低、互换性好和轻量化等优点[1]。面齿轮齿面形状复杂，其精加工一般采用磨削，但砂轮磨削面齿轮时会产生大量的热量，冷却后有残余应力，导致齿面变形，从而降低疲劳强度和抗应力腐蚀性能，严重时会产生裂纹，影响加工质量和使用传动性能[2]。因此，国内外学者对面齿轮磨削方法进行了研究。Gleason公司提出利用CONIFLEX砂轮磨削面齿轮，即利用碟形砂轮模拟插刀的一个齿，对面齿轮做点接触展成运动，此方法属于单分度展成磨齿方法[3]。王延忠等[4]研究了用渐开线蝶形砂轮对面齿轮进行数控磨削加工的方法，并设计了磨削面齿轮机床。彭先龙等[5]根据蝶形砂轮磨削面齿轮的基本原理，设计了面齿轮磨削加工工艺，仿真模拟了整个砂轮磨削加工过程。

研究残余应力一般有3种方法：有限元分析法、解析法和实验法，其中有限元分析法是一种较有效的方法[6]。A. Brosse等[7]通过对特定材料GCr15的磨削来分析热对残余应力的影响，并构建了力热耦合模型。吴吉平等[8]基于热弹塑性理论，对螺旋锥齿轮磨削进行了力热耦合有限元仿真和实验研究，得到磨齿残余应力的变化规律。Ren X. Z. 等[9]基于矩形和三角形移动热源理论，建立了成形磨齿热量分配比模型，推导出计算磨削区域最高温度公式。K. D.Bouzakis等[10]针对直齿和斜齿圆柱齿轮干切滚齿过程中切屑的形成与流动，建立了力热耦合有限元模型。王延忠等[11]对齿轮材料18Cr2Ni4WA进行磨削加工实验，并通过ABAQUS有限元分析软件进行仿真，得到了材料18Cr2Ni4WA的磨削烧伤临界温度。H.Hamdi等[12]建立了钢AISI 52100进行磨削时的力热耦合2D模型，得出传统磨削下表面残余应力的变化规律。Miao H.等[13]得出钢NAK80磨削后喷丸工艺的表面残余应力分析模型，并采用X射线衍射法进行实验研究。

以上研究主要以简单零件车削、铣削和螺旋锥齿轮磨削等残余应力研究为主。面齿轮具有理论上定传动比和形状不同的齿宽方向等相异特征[14]。目前，关于面齿轮磨削力热耦合作用的表层残余应力研究成果的报道较少，故本课题组对此进行研究。

1 面齿轮磨削残余应力的产生机理及分析方法

面齿轮磨削过程中受磨粒与齿面之间力热作用的影响，磨削加工表层会产生较大的热弹塑性变形。面齿轮磨削残余应力产生的原因有两方面：一是磨削时磨粒切削刃具有大的负前角，在外加力载荷作用下，磨削表层出现不均匀塑性变形，产生残余应力；二是磨削热会使磨削表层发生热膨胀，冷却后在工件表层产生残余拉应力。此外，磨削热还会使磨削表层材料金相组织产生变化，但正常加工时磨削温度不高，相变对齿面残余应力的影响不大[15]。

磨削时生成齿面表层残余应力，可认为是移动集中力和热对齿面作用下的热弹塑性力学问题[16]。根据热弹塑性理论的Prandtl-Reuss方法，磨削过程中工件处于热弹塑性状态下的全应变增量包括弹性应变增量、塑性应变增量和温度应变增量，磨削表层热弹塑性力学本构关系可表示如下：

弹性区

塑性区

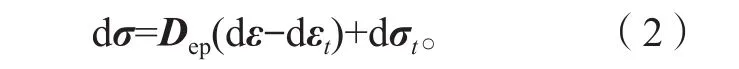
式（1）～（2）中：dσ为应力张量；dε为应变张量；dεt为温度应变张量矩阵；dσt为温度应力张量矩阵；D、Dep分别为材料的弹性矩阵和塑性矩阵。

由于热弹塑性的应力应变关系为非线性，故通过增量载荷法将式（1）、（2）线性化，即：

弹性区

塑性区

式（3）～（4）中：Δσ、Δε分别为应力增量和应变增量；Δσt、Δεt分别为温度应力增量和温度应变增量。

Δσt、Δεt可分别作为一般的初应力与初应变转换为等效节点载荷，即：

弹性区

塑性区

式（5）～（6）中：ΔRe、ΔRep分别为初应力与初应变的等效节点载荷；B为几何矩阵；s为节点区域。

齿面还受到外部节点力载荷ΔRd、分布载荷ΔRp和体力载荷ΔRf的作用，则节点总等效载荷ΔR为

由此得出总的热弹塑性平衡式方程的矩阵表达式为

式中：k为总刚度矩阵；Δu为节点位移增量。

由式（8）求出节点位移增量Δu，再由位移增量和应变增量之间的关系求得应变增量；最后由式（3）或式（4），求出应力增量Δσ。

2 影响面齿轮磨削残余应力的基本参量数学模型

碟形砂轮磨削面齿轮为单分度展成磨齿方法，碟形砂轮与齿面的接触方式为点接触磨削。磨削设备为五轴联动数控磨床QMK50A，其数控系统为Siemens 840，正交面齿轮材料为18Cr2Ni4WA，采用Al2O3碟形砂轮，磨削外观如图1所示。影响磨削残余应力的基本参量主要有磨削接触椭圆方程参数、磨削力和磨削热流量等。

图1 蝶形砂轮磨削面齿轮Fig. 1 The scene diagram of face gear grinding by dish wheel

2.1 磨削接触椭圆方程参数

根据Gleason接触原理，碟形砂轮磨削工件时磨削点的瞬时接触形状为椭圆[17]，如图2所示。椭圆中心是磨削点的位置，椭圆长轴a、短轴b分别为面齿轮磨削接触弧长和磨削接触宽度。为计算a、b，需先确定接触齿面的主曲率、主方向。

图2 面齿轮磨削点瞬时接触椭圆Fig. 2 The instantaneous contact ellipse of grinding point of face gear

1）齿面磨削接触主曲率与主方向

齿面上任意一点P的法曲率不同。取点P的两个极值作为该点的主曲率，其对应的方向为主方向。齿面Σ上P点法曲率ρn[18]为

式中：k为齿面Σ上曲线r=[θs, φs]的P点曲率；θ为齿面Σ上P点单位法矢n与曲线r上P点单位法矢之间的夹角；(θs, φs)为齿面Σ上P点坐标；Ι为齿面Σ的第一基本二次型；Π为齿面Σ的第二基本二次型；E、F、G为齿面Σ的第一基本二次型变量；L、M、N为齿面Σ的第二基本二次型变量，且

2）瞬时接触椭圆长、短轴

面齿轮磨削瞬时接触椭圆受到磨削深度、磨削时的弹性形变的影响。磨削齿面接触椭圆的相关参数如图3所示，Σ、η为公切面上的两坐标轴，ρ1、ρ2为主方向矢量，σ为ρ1与坐标轴η的夹角，αs为ρ1和ρ2之间的夹角。

图3 磨削齿面接触椭圆的相关参数Fig. 3 Contact ellipse parameters of tooth surface

瞬时接触椭圆长轴a、短轴b的计算公式为

2.2 面齿轮磨削力和磨削热流量的数学模型

1）磨削力

面齿轮磨削主要包括滑擦、耕梨、切削3个过程，磨削力存在3个分力，即沿砂轮的磨削纵向分力Fa、磨削法向分力Fn和磨削切向分力Ft，其中Fa较小，可忽略不计。磨粒负前角大，因而Fn大于Ft，磨削法向分力Fn主要受加工质量和接触变形影响，一般Fn/Ft=1.9～2.6[19]；磨削切向分力Ft会对磨削的磨损和动力消耗产生影响，可由经验公式[20]得出

式中：Fp为单位磨削力；ap为磨削深度；vs为砂轮切向速度；vw为展成速度；b为磨削接触短轴；A′、B′、C′、δ′为经验公式指数。

2）热量分配系数

面齿轮磨削过程中磨削时间短、磨削速度高，可将磨削过程中工件与砂轮接触的每一对应点的温度视为连续。干磨下传入工件的热量分配系数Rw计算公式[4]为

式中：λs为磨粒导热系数；βw为材料的热特性；re为磨粒接触有效半径。

磨削液对磨粒使用状况（破损率、有效磨粒数）、磨削接触弧长和接触宽度等影响较大，因而对Rw的影响也较大，施加磨削液后可减少传入工件的热量。有磨削液时一般取Rw=0.6～0.8。

3）磨削热流量

面齿轮磨削接触弧长较小，可将磨削热问题看作一个带状热源在半无限体表面上移动。根据JAEGER热源理论，磨削热载荷用呈矩形分布的移动线热源[14]，其磨削热流量q为

式中，逆磨时取“+”号，顺磨时取“-”号。

3 面齿轮磨削力热耦合有限元仿真

3.1 磨削温度场有限元仿真

对面齿轮磨削残余应力影响较大的磨削温度场，是磨削时各种热源产生的磨削温度在空域和时域分布的一个集合，可看作一个由非稳态温度场到稳态温度场的渐变过程[15]。受多因素相互作用影响，采用有限元分析法分析磨削温度场是一种有效途径。

正交面齿轮主要参数如表1所示。采用逆式干磨对正交面齿轮进行磨削，磨削温度场工艺参数如表2所示，其中磨削切向分力Ft由经验公式（17）算出。根据碟形砂轮磨削加工原理，面齿轮各个齿的对应磨削点的温度分布情况基本相同。因此，分析面齿轮磨削温度场时，先建立单齿3D实体模型，选用SOLID95单元类型进行网格划分，得到单齿3D有限元模型，如图4所示。

图4 单齿3D有限元模型Fig. 4 The 3D finite element model of single tooth

表1 正交面齿轮主要参数Table 1 Main parameters of orthogonal face gear

表2 磨削温度场工艺参数Table 2 Process parameters of grinding temperature field

在磨削温度场有限元仿真中，先在边界上加载温度载荷，再在边界上贴上一层表面效应单元以施加磨削热流量q载荷。磨削载荷移动采用小步距移动法来模拟载荷移动，即把砂轮与工件的接触弧长分成若干个载荷步，每个载荷步又分为n个子载荷步，当进行到第n个子载荷步时，将磨削热流量q及磨削力Ft载荷施加在该载荷步区域的所有单元上，并以展成速度vw沿齿面切向运动。

由于面齿轮齿面形状为空间曲面，同时磨削参数（如磨削接触弧长、磨削接触宽度、磨削力和磨削热流量等）在每个点各异，仿真分析时可根据旋转投影面对齿面网格沿齿长方向九等分、齿高方向五等分，对齿面的45个点进行仿真，如图5所示。本研究选取具有代表性的5个点（A、B、C、D、E）的磨削温度场进行分析。

图5 面齿轮磨削有限元仿真分析点Fig. 5 Analytical points of finite element simulation of face gear grinding

用ANSYS软件进行温度场仿真时，需设置材料属性，设定瞬态温度分析的初始条件、热约束条件和热载荷，确定载荷步。由式（16）得到磨削接触弧长a′=0.668 2 mm，磨削热流量加载时间 t=a′ /vw=0.003 4 s，在磨削接触弧长上分5个载荷步，每个载荷步时间为0.000 68 s。由式（18）得干磨时热量分配系数Rw=0.886。由式（19）得磨削热流量 q=2.214 6×107W/m2。C点的磨削温度场分布云图如图6所示。由图可知，磨削齿面C点的瞬态最高温度为297.926 ℃，处于磨削点接触弧中心区域。

图6 磨削齿面C点的温度场分布云图Fig. 6 Distribution cloud chart of grinding temperature field of point C of tooth surface

3.2 磨削残余应力有限元分析

为使磨削残余应力的有限元仿真高效和精确，采用力热耦合间接分析法，即先分析温度场，再将温度场结果作为条件载荷来施加，通过力热耦合分析应力场。主要包括两个过程：第一个过程是通过施加热对流和热流密度，得到磨削瞬态温度场，然后经热/结构转换，通过后处理导入磨削瞬态温度场的结果，施加磨削力，得到在磨应力分布；第二个过程是磨削瞬态温度冷却，通过热/结构耦合后，卸去所有载荷，初始应力为导入的在磨应力，求解磨削残余应力。

当磨削面齿轮的材料和加工条件（设备、砂轮、磨削方式等）一定时，对面齿轮表层残余应力影响较大的为磨削用量和冷却条件，故本研究中冷却采用水基磨削液。

1）磨削深度

当 vw=1 m/min，vs=20.6 m/s时，磨削深度 ap分别取 0.01, 0.03, 0.05 mm，选取齿面上磨削点 A 处节点 5885 以及点 A 处附近沿齿厚方向的 13 264, 12 548,6625节点，经有限元仿真得到磨削残余应力分布如图7所示。由图可知，齿面上为残余压应力，齿里层为残余拉应力；ap取值越大，齿面残余应力增大显著。这是由于ap值较大时，磨削力和磨削热流量较大，使得力在工件接触处作用的时间增加，导致磨削温度增高，残余应力增加显著。

图7 不同ap下残余应力仿真值分布Fig. 7 Distribution of simulated residual stress values under different ap

2）砂轮速度

当 vw=1 m/min，ap=0.02 mm 时，砂轮速度 vs分别取 20, 30, 50 m/s，选取点A及其附近的同样 4 个节点，经仿真得到残余应力分布如图8所示。由图可知，随vs的增大，齿面磨削残余应力增大明显。这是由于vs增大时，磨削热流量增大，磨削温度较高，引起热应力增大，从而导致残余应力增加明显。

图8 不同vs下残余应力仿真值分布Fig. 8 Distribution of simulated residual stress values under different vs

3）展成速度

当ap=0.02 mm，vs=20 m/s时，展成速度vw分别取 1, 3, 8 m/min，选取点A及其附近的同样 4 个节点，仿真得到的磨削残余应力分布如图9所示。由图可知，随着vw的增大，齿面残余应力增幅减小。这说明在vw增大时，磨削力增大，但磨削热量分配系数Rw减小，导致磨削热流量增加不多，载荷作用时间减小，进而使磨削温度降低，导致齿面残余应力增幅减小。

图9 不同vw下残余应力仿真值分布Fig. 9 Distribution of simulated residual stress values under different vw

另外，通过力热耦合有限元分析，采用水基磨削液等湿磨时比干磨的磨削残余应力明显减小。这是因为湿磨时，滑动摩擦系数减小，导致切向磨削分力Ft稍有减小，热量分配系数Rw和磨削热流量q显著减少，磨削温度下降，由力热耦合引起的应力降低，从而使磨削表层残余应力减小。

4 实验部分

4.1 实验方法与条件

磨削表层残余应力测量实验采用X射线衍射法。其基本原理是先测量衍射线位移，即残余应变，然后根据胡克定律将应变转换成残余应力。

实验条件采用与磨削残余应力有限元仿真时相同的磨削条件及齿坯参数，实验仪器采用日本理学转靶X射线衍射仪D/max 2550（18 kW），如图10所示。实验前，将磨出的面齿轮用线切割切出一个齿样，用酒精擦拭齿面，干净后，将齿样固定在衍射仪工作台上。实验时，使用Cu靶辐射源，X射线波长λ为 0.154 06 mm，管流为 300 mA，管压为 40 kV，倾斜角ψ依次取值 0°, 10°, 20°, 30°，扫描角度为131°～142°。

图10 转靶X射线衍射仪D/max 2550Fig. 10 Target X-ray diffraction instrument D/max 2500

4.2 实验结果与分析

实验中，面齿轮磨削用量如下：ap=0.02 mm，vs=30.5 m/s，vw=1 m/min。齿面 上点A及其附近的 4个节点的残余应力实测值与仿真值的对比分析如表3和图11所示。

图11 面齿轮磨削残余应力的实测值与仿真值对比曲线Fig. 11 Contrast curve of measured values and simulated ones of grinding residual stress of face gear

表3 面齿轮磨削残余应力实测值与仿真值的对比分析Table 3 Contrast analysis of measured values and simulated ones of residual stress of face gear

由表3和图11可以看出，当距离磨削点深度为0 μm时即齿面位置，实测值与仿真值的相对误差最大，为17.8%，造成这种情况的原因主要有两方面：一是仿真分析时有一定的条件假设和简化处理，从而使仿真值与实测值有差别；二是测量本身的误差，主要是X射线衍射法的倾斜角选择和透射深度有限等会造成一定误差。但从数据分析看，较小的相对误差在控制范围内，说明利用力热耦合进行有限元仿真分析的研究有效。

5 结论

1）研究了产生面齿轮残余应力的影响因素和机理，根据碟形砂轮磨削面齿轮的加工方法和Gleason接触原理，分析了接触椭圆的长短轴，利用经验公式计算了磨削力，采用矩形分布的移动线热源求解磨削热流量。

2）根据面齿轮磨削单齿3D有限元模型，采用小步距移动法模拟磨削载荷的移动，对磨削温度场进行有限元仿真，仿真结果表明磨削瞬态最高温度位于磨削接触弧中心区域。采用力热耦合间接法仿真分析磨削表层残余应力，得磨削齿面上为残余压应力，齿面里层为残余拉应力。磨削用量和冷却条件对残余应力的影响呈现一定的规律，磨削深度ap和砂轮速度vs对磨削残余应力的影响较大，随ap和vs的增大，齿面残余应力增加显著；但随展成速度vw的增大，齿面残余应力增幅减小；湿磨时比干磨的磨削残余应力明显降低。

3）采用X射线衍射法实验，对面齿轮磨削表层残余应力的实测值与仿真值进行了对比分析。实测值与仿真值之间的相对误差最大值为17.8%，说明采用力热耦合的有限元分析有较好的精度。本研究为提高面齿轮磨削质量提供了行之有效的方法。