啮合刚度和径向支承刚度对复合行星轮系均载的影响比较

张海波 杨 超

周 贤1 刘克非1

蔡 颂3 明兴祖3

1. 湖北文理学院

机械工程学院

湖北 襄阳 441053

2. 清研新能源汽车工程中心（襄阳）有限公司

技术研发部

湖北 襄阳 441100

3. 湖南工业大学

机械工程学院

湖南 株洲 412007

0 引言

复合行星轮系广泛应用于包装机械设备中。相对于简单行星轮系，复合行星轮系自身构件多，制造与装配精度要求较高，其动态特性更容易受到内部激励的干扰，尤其是来自周转轮系内部的时变啮合刚度激励以及构件径向支撑刚度激励，刚度幅值取值的合理性直接关系到复合行星轮系功率分流性能。当前针对周转轮系均载性能的研究，多采用单因素分析模型分析单个激励变化对均载的影响，忽略了不同类型的激励因素同时变化对均载的综合影响。A. Kahraman等[1]分析了啮合刚度变化对2KH行星轮系均载系数的影响；A. N. Montestruc[2]研究了行星轮支撑刚度对简单行星轮系载荷分配性能的影响。以上文献表明：1）尽管已有文献记录了刚度激励对周转轮系均载的影响，然而所研究对象并未涉及复合行星轮系；2）针对均载的研究方法普遍采用单因素分析法，缺乏了解轮系在多变量同时变化下的均载行为，有必要建立均载分析的多因素分析模型。

本文在比较啮合刚度幅值和不同构件支撑刚度幅值对均载影响效果的基础上，推导并建立含行星轮平移的拉维娜式复合行星轮系集中参数动力学模型；采用数值法求解运动方程和均载系数；结合田口实验法，设计控制变量和直交序列；通过信噪比分析和方差分析，调查轮系在不同类型刚度激励同时变化下的均载性能。

1 动力学建模

为研究不同类型的刚度激励对均载性能的综合影响，本文以拉维娜式复合行星齿轮传动系统为研究对象，第二类拉格朗日方程为理论依据，推导并建立了含行星轮平移振动的复合行星轮系平移-扭转动力学模型。该动力学模型的建立参考并拓展了D. R.Kiracofe等[3]的广义复合行星轮系动力学模型以及巫世晶等[4]的不含行星轮平移的复合行星轮系动力学模型，旨在体现行星轮的径向支撑刚度对轮系平移振动的影响，以便将径向支撑刚度的对象按照中心构件和行星轮加以区分。所建立的拉维娜式复合行星轮系动力学模型如图1[4]所示。

图1 复合行星轮系平移-扭转动力学模型Fig. 1 translation and rotation dynamic model of compound planetary gear set

图1 所示的动力学关系中：中心轮s1作为轮系转速的输入端，与行星轮an（n为均布行星轮的数目）啮合形成啮合副。行星轮an和bn共同依附在行星架c上，并组成行星轮-行星轮啮合副。行星轮bn是具有两种齿数和的长行星轮，在齿数端与内齿圈r啮合，形成啮合副，在齿数端与轮系负载输出端的中心轮s2啮合，形成啮合副。沿啮合线方向上，由时变啮合刚度 kj（j=s1, an、s2, bn、an,bn、r,bn）、传递误差ej以及啮合阻尼cj，共同组成连接各啮合齿轮的弹簧阻尼单元。该动力学模型内所有构件的平移振动 (xi, yi)（i=s1、s2、an、bn、c）都是在旋转坐标系xOy下测量得到的，该坐标系依附于行星架c上，正方向指向第一个行星轮a1的旋转中心，并以ωc的角速度同行星架一起旋转。

该动力学模型内所有构件的扭转振动θi（i=s1、s2、an、bn、c）是在绝对坐标系XOY下测量得到的。为了平衡动力学模型内部各参数值之间的数量级，引入位移标称尺度bw以及时间标称尺度bt对轮系内部各参数进行无量纲化处理。依据第二类拉格朗日方程以及牛顿运动定律，系统无量纲化处理后的各构件运动方程如下：

中心轮s1的运动方程

ψj为旋转坐标系 xOy下，x轴方向与啮合副Pj啮合线的夹角；

θi为构件i 在绝对坐标系XOY下的扭转角位移；

mi（i=s1、s2、c、r、a、b）为构件的质量；

ri为各个齿轮的基圆半径；

mce为包含行星轮an和bn的行星架等效质量；

Jm（m= s1、s2、ce、r、a、b）为转动惯量，假定所有均匀布置的行星轮的质量以及转动惯量相同，其中Jce是包含行星轮an和bn的行星架的当量转动惯量，

式（7）中rc,a、rc,b分别为行星轮 an与 bn旋转中心到行星架c旋转中心的距离；

kj fjsinψj（j=s1, an、s2, bn、an, bn、r, bn）是不同啮合副的啮合力向绝对坐标系XOY的X轴投影，其中fj描述存在于啮合副Pj内的齿侧间隙对实际啮入深度的影响，并采用经典的分段函数定义，

式（8）中，δj为啮合副Pj的理论相对啮合位移，bj为齿侧间隙大小（视为恒定）。

各个啮合副的啮合刚度幅值与齿侧间隙函数的乘积即为各个啮合副的啮合力。根据式式（1）～（6）中对中心构件的支撑反力和行星轮的支撑反力的描述，中心构件和行星轮的支撑反力Fi可以描述为：

当i=s1、s2、c、r时

当i=an、bn时

式（9）～（10）中ki为构件i处的径向支撑刚度。

由于行星轮在自转的同时，会随行星架做绕原点O的平面旋转运动，因此在描述行星轮支撑弹簧的位移变形时，会考虑行星架c的振动位移，如式（10）所示。

2 田口实验

为研究啮合刚度和径向支撑刚度对轮系载荷分配性能的综合影响，在已有的复合行星轮系动力学模型的基础上，首先建立复合轮系均载性能的多因素分析模型。田口实验法旨在量化和分析多个变量共同作用下的输出性能，且不受模型算法的制约，是进行均载性能多因素分析最合适的理论方法之一。为探索不同类型的刚度激励对均载的综合影响，本研究将田口实验理论与复合行星轮系的动力学模型相结合，以输入和输出的中心轮的均载系数为分析目标，所有啮合副的啮合刚度幅值、中心构件的径向支撑刚度幅值以及行星轮的径向支撑刚度幅值为控制变量。根据L18(33)直角序列配置不同控制变量的水平取值，并引入复合轮系动力学模型计算相应的均载系数。采用三维云图、信噪比分析和方差分析，横向对比各控制变量对均载系数的影响，找出影响均载性能的最重要控制变量，以及对应的水平。

2.1 均载系数的定义和计算

采用龙哥库塔数值法求解复合行星轮系的常微分运动方程组（1）～（6），得到各啮合副随时间变化的啮合力fj，用来定义均载系数Bm，以衡量中心轮载荷分配性能优劣。

由啮合副Pj的时变啮合力fj，经式（11）计算得到中心轮i在任意时刻下的均载系数Bj(t)，然后取一段时间内的均载系数的最大值Bm，作为衡量该中心轮载荷分配性能优劣的均载系数。这样定义均载系数与之前文献[1-2]中定义不同，主要是为了体现轮系载荷分配的性能的实时性。这种均载系数定义的可行性，将在后续的结果分析中通过文献对比的方式加以论证。本文的分析目标是中心轮s1和s2的均载系数

2.2 控制变量和直交序列

根据田口实验理论，为衡量啮合刚度和支撑刚度对复合轮系均载性能的影响效果，设计控制变量水平的数目和取值（见表1），使控制变量的不同取值能够对轮系的均载性能产生显著变化。据文献[1-2]的结果分析，啮合刚度幅值以及径向支撑刚度幅值的变化范围取2×1010～8×1010N/m，周转轮系的动态特性发生显著的变化。

表1 控制变量和相应水平Table 1 Control parameters and their levels 1010 N/m

表1中，3组控制变量同属于刚度激励的范畴，其取值的数量级和对轮系动力学模型的作用机理相近，适合用来比较不同的激励对均载的作用效果。将各控制变量的水平按照L18直交序列的规则进行分布，并按照实验编号的顺序依次引入复合行星轮系的运动方程（1）～（6）中，计算输入中心轮s1的均载系数和输出中心轮s2的均载系数，以及相应的信噪比，其结果如表2所示。

表2 L18直交序列和实验结果Table 2 Results of experiments and L18 orthogonal table

3 结果分析

3.1 信噪比分析

田口实验法采用丢失函数衡量理论值与真实值的误差，这类丢失函数可以进一步的理解为信噪比（S/N）[6]。通常有3种衡量分析质量的信噪比模型，“lower-the-better”“the higher-the-better” 和“the nominal-the-best”[7]。基于信噪比值，对于每一个控制变量进行信噪比分析。为了使系统的均载性能最优化，即均载系数降到最低，故采用“lower-the-better”信噪比模型进行计算，其计算法则如式（13）所示。

控制变量的不同水平所对应的平均信噪比，按照文献[8]的方法计算，结果如表3所示。由表3可知，每一种控制变量（A、B、C）都有较大的信噪比水平值，这表明控制变量取该水平值对啮合副的均载性能较好[8]。为了使输入中心轮s1和输出中心轮s2的均载性能最好，可以使各个控制变量取第一个水平，即所有刚度激励的幅值越小，均载性能越好。

表3 控制变量各水平的平均值信噪比Table 3 Average S/N response table

为了更好地了解每个控制变量对均载的影响，掌握均载随控制变量的变化趋势，绘制出均载系数的要因效果图，如图2所示。

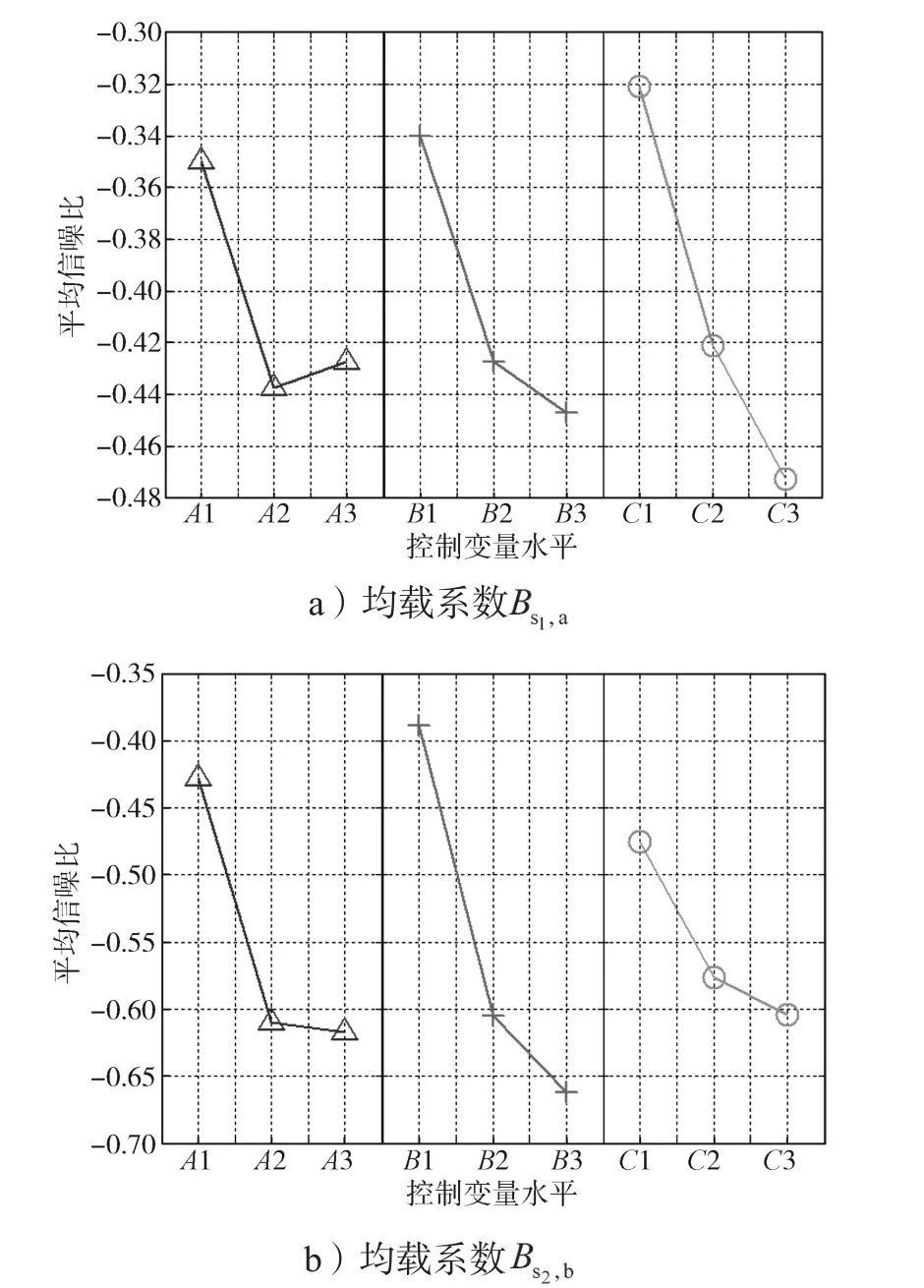
图2 均载系数的要因效果图Fig. 2 The main factor effect diagram of load sharing coefficient

由图2可知：随着啮合刚度水平值的增加（A1～A3），均载系数的平均信噪比由下降到趋于平稳，表明啮合刚度幅值的增加会降低轮系的均载性能，但增大到一定幅值（5×1010N/m）后，对均载的影响可以忽略；随着中心轮s1和s2以及行星轮的支撑刚度增加，均载系数的平均信噪比减小，均载系数增大，这表明构件支撑刚度幅值的增加不利于提升轮系均载性能。除此之外，通过对比3种控制变量平均信噪比的波动幅值发现，控制变量C的变化能引起均载系数的较大变化；控制变量B的变化能引起均载系数的较大波动。

3.2 方差分析

方差分析是一种数理统计方法，主要用于在设计过程中分析多因素变量之间的相互作用关系。本文分析内部激励和外部激励对均载影响的贡献度，采取95%的置信区间。F检测能够根据其指定的置信度，找出每一个影响因子对结果的贡献度；每一个控制变量对均载系数影响的贡献率取决于F测试的结果。方差分析结果如表4所示。

表4 方差分析结果Table 4 Results of analysis of variance

由表4可知，控制变量A、B、C对均载系数的贡献率分别是18.96%、26.86%、49.61%，对均载系数影响最大的控制变量是行星轮的支撑刚度。相比于啮合刚度幅值（控制变量A的贡献率为27.45%）和行星轮支撑刚度幅值（控制变量C的贡献率为11.09%），中心轮s1和s2的支撑刚度对均载系数产生了较大的影响（控制变量B的贡献率为49.09%）。

由信噪比分析和方差分析的结果可知，在3个控制变量中，相比于所有啮合副的啮合刚度幅值，中心轮s1和s2的支撑刚度幅值和行星轮的支撑刚度幅值对轮系均载的影响较大。行星轮的an和bn的支撑刚度（贡献率49.61%）是影响均载系数的最关键因素，中心轮s1和s2的支撑刚度是决定输出中心轮s2的载荷分配性能的最关键因素（贡献率49.09%），啮合刚度幅值的变化对均载的影响要小很多。产生这种现象的主要原因在于啮合刚度幅值的变化并不针对某个功率传递线路上的作用力，而是针对所有啮合副，因此并未对功率分流性能产生较大影响；而降低构件的支撑刚度，相当于对传递载荷的轮系构件起到构件浮动的效果，增大构件的浮动量可以明显改善系统的均载特性[8]，与相关文献的记载一致。这就验证了本文所建立的动力学模型的正确性，以及所定义的均载系数的可行性。

然而，方差分析的结果仍未能给出决定复合行星轮系均载性能的最关键激励。为更清晰地比较控制变量对均载的作用效果，需要研究2个控制变量同时变化时，均载系数的变化规律，如图3所示。

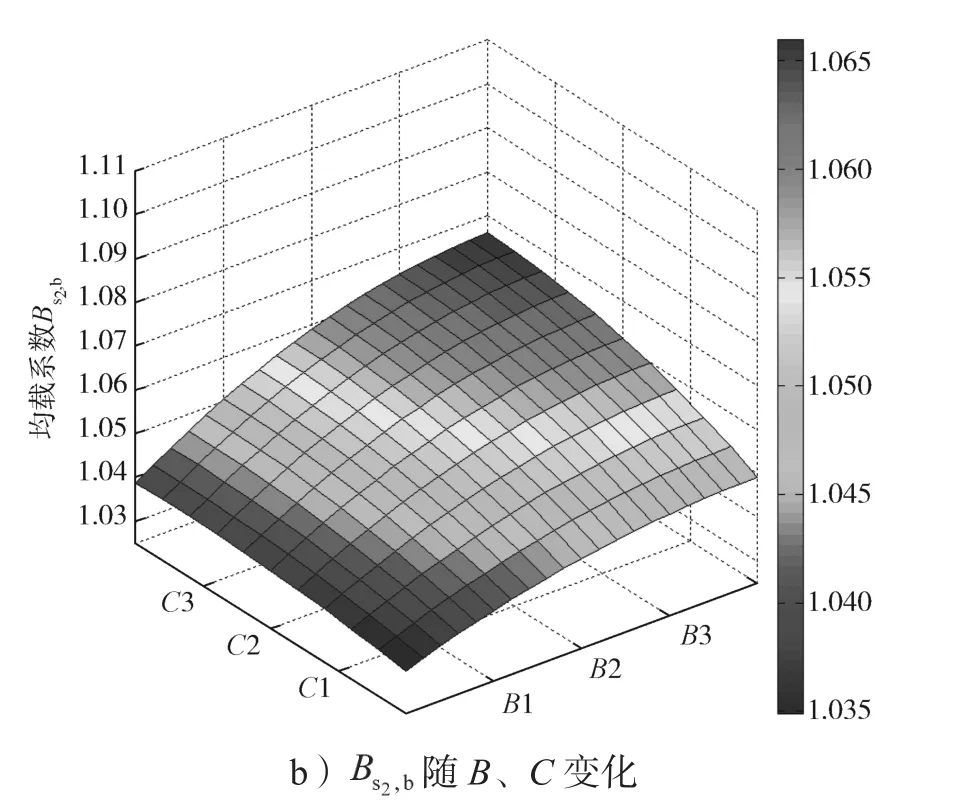
图3 均载系数随2个控制变量的变化云图Fig. 3 The changing cloud diagram of load sharing coefficient with two control variables

由图3可知：随着3个控制变量（A、B、C）坐标值的增加，均载系数和，在局部和整体上都呈上升的趋势，这说明轮系的均载性能会随着啮合刚度以及支撑刚度幅值的增加而降低，这与之前3.1节的结论吻合。相对于不同的控制变量，均载系数的上升梯度各不相同，说明不同控制变量对轮系均载性能的影响程度存在显著差异；在相同的激励配置下，的值和变化梯度大于，表明输出中心轮s2的载荷分配性能更容易受到来自刚度激励的影响，而依据方差分析的结果，控制变量B（中心轮s1和s2的径向支撑刚度幅值）是决定均载系数的最关键因素。

4 结论

综上所述，可得以下结论：

1）啮合刚度幅值的增加会降低轮系的均载性能，但是当增大到5×1010N/m后再继续增加，基本不影响轮系的均载性能；增大中心轮s1和s2的支撑刚度幅值，会降低轮系的均载性能。

2）在激励变化幅度相同的情况下，与输入中心轮s1相比，输出中心轮s2的均载系数变化更加剧烈，因此采用来衡量本复合轮系均载性能的指标。

3）田口实验与方差分析的结果表明，中心轮s1和s2的支撑刚度是决定复合轮系均载性能最重要的刚度激励，其次是行星轮的支撑刚度和所有啮合副的啮合刚度。

4）本文所建立的复合行星轮系多因素分析模型，可以用来研究轮系的动态特征在不同类型激励因素作用下的变化规律，定量比较各激励对动态指标的影响权值，找出决定动态指标的最关键因素。