基于ASSD-MOMEDA-FWEO相结合的滚动轴承故障诊断

唐贵基，丁 傲,，王晓龙，张 晔

(1.华北电力大学机械工程系，河北 保定 071003；2.国网吉林省电力有限公司长春供电公司，吉林 长春 130021)

0 引言

滚动轴承作为旋转机械中的重要组成部分，支撑着整个设备的安全、可靠运行[1]。因其常常处于高温重载的恶劣工作环境之中，易出现表面损伤。轴承损伤会引发整个机械系统异动，造成设备停机，威胁人身安全。轴承的早期故障信号中冲击成分微弱，而实际运行中背景噪声广泛存在，且信号在传输中会被衰减，所以采集到的信号信噪比低，故障特征提取困难。在准确识别轴承故障类型方面，从原始振动信号中提取微弱故障特征信息一直是轴承故障诊断领域的热点[2]。

目前，经验模态分解、局部均值分解、固有时间尺度分解等频带划分信号处理算法，难以精细分析故障信号高频区域，且存在虚假分量、曲线失真等问题；共振稀疏分解、经验小波变换、变分模态分解等非递归式信号处理算法，分解效果受复杂的参数设置制约。2014年，Bonizzi等[3]提出奇异谱分解(singular spectrum decomposition，SSD)。该方法通过重新定义轨迹矩阵来增强信号的振荡分量：根据信号特征自适应选取轨道矩阵嵌入维数，对轨迹矩阵主成分进行奇异值分解及特征重组，将信号分割为由高频至低频的若干奇异谱分量(singular spectrum component，SSC)。SSD算法为非平稳非线性机械故障信号处理提供了新思路，目前已有学者对其进行研究。文献[4]将SSD算法与一维卷积神经网络(1 dimension convolutional neural network,1DCNN)算法相结合，诊断恒速工况下滚动轴承故障。文献[5]将SSD算法应用于齿轮箱复合故障诊断中。文献[6]将SSD算法与奇异值分解相结合，用于齿轮故障特征提取。文献[7]将SSD算法用于风电机组驱动系统多通道故障诊断。

然而，SSD算法需人为设置奇异谱分量个数K。若K值过小，信号分解不充分；若K值过大，会出现虚假分量。针对该问题，本文提出了自适应奇异谱分解(adaptive singular spectrum decomposition，ASSD)。ASSD采用合成峭度与斯皮尔曼等级相关系数(Spearman rank correlation coefficient,SRCC)作为联合判据，实现奇异谱分量个数K的自适应确定。

滚动轴承故障信号周期性冲击提取可视为源信号与信道解卷积的过程。Wiggins提出最小熵解卷积(minimum entropy deconvolution，MED)算法。但MED算法倾向于单点脉冲而非周期性脉冲的提取。此后，McDonald提出了最大相关峭度解卷积(maximum correlate kurtosis deconvolution，MCKD)算法。相较MED算法而言，MCKD算法增加了局部有限脉冲数。2017年，McDonald进一步提出了多点最优最小熵反褶积(multipoint optimal minimum entropy deconvolution adjusted，MOMEDA)算法，以D-范数最大为目标，根据预先估计的故障频率构建目标向量。与MED算法和MCKD算法相比，MOMEDA算法在对周期性冲击信号特征提取方面的优势更为明显[8]。

2014年，O’Tooley提出频率加权能量算子(frequency weighted energy operator，FWEO)算法，利用信号的谐波特性，通过计算信号导数的包络，得到信号的瞬时能量估计。与希尔伯特变换和传统能量算子相比，FWEO算法的计算复杂性低，具有更好的抗干扰特性[9]。

鉴于上述分析，针对强噪声背景下的滚动轴承故障诊断问题，本文提出1种ASSD-MOMEDA-FWEO相结合的方法：利用ASSD算法对原始信号进行预处理，从中筛选出信噪比较高的最佳奇异谱分量；利用MOMEDA算法和FWEO算法作为后处理策略，进一步放大故障特征，实现滚动轴承微弱故障的准确判定。

1 基本原理介绍

1.1 SSD算法

SSD作为一种新型信号处理方法，能将非平稳非线性信号从高频至低频依次分解为一系列奇异谱分量和残余分量的线性叠加。具体分解过程如下。

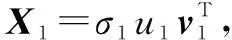
为更好地估计主峰带宽Δf，利用基于3个高斯函数混合的谱模型拟合功率谱密度轮廓，即：

(1)

式中：Ai为第i个高斯函数的幅值；ui为位置；σi为宽度；θ=[Aσ]T为参数向量且满足A=[A1A2A3]和σ=[σ1σ2σ3]。

(2)

当比重小于给定阈值时，则终止迭代。否则，将残余分量作为原始信号重复迭代过程，直至满足停止条件。最终获得K个SSC分量。原始信号可表示为如下形式：

(3)

1.2 MOMEDA算法

MOMEDA算法是在MED算法的基础上开发的。滤波后的实际信号yn为：

(4)

(5)

MOMEDA算法利用目标向量和D-范数重新定义了多点D范数(multi D-norm，MDN)指标：

(6)

将最小熵解卷积问题变为求解多点D范数最大化问题：

(7)

式中：t为确定冲击成分的位置和权重的目标向量。

对式(7)求解，可得：

(8)

取其特解作为一组最优滤波器：

(9)

将式(9)代入式(4)，得到原始冲击信号为：

(10)

1.3 FWEO算法

FWEO算法的基本原理如下：

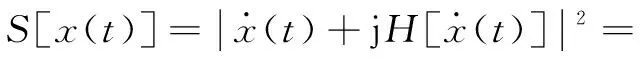
(11)

式中：S()为信号的复包络；H()为希尔伯特变换；φ[x(t)]为频率加权能量算子。

振动信号的调幅-调频信号的表达式为：

x(t)=Acos(ωt+φ)

(12)

根据式(12)可知：

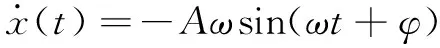
(13)

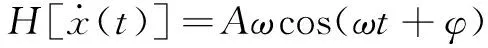
(14)

将式(13)、式(14)代入式(11)，可得：

φ[x(t)]=[Aωsin(ωt+φ)]2+

[Aωcos(ωt+φ)]2=A2ω2

(15)

2 自适应奇异谱分解方法

2.1 合成峭度

轴承发生故障时，故障表面与其他元件发生周期性接触。此时，振动信号中故障成分具有冲击性和循环平稳性双重特性。时域峭度对冲击性敏感，忽略了循环平稳性，而包络谱峭度可评价信号的循环平稳性。本文采用包络谱峭度和时域峭度构成得到的合成峭度指标[10]。其定义如下：

KE=KES·Kku

(16)

(17)

式中：KE为合成峭度；Kku为峭度；KES为包络幅值峭度；SE(j)为采样点j的信号包络谱；p为包络谱的采样点数。

2.2 斯皮尔曼等级相关系数

SRCC是用于评价2个变量之间相关性的1种非参数、无分布的秩统计度量方法[11]，将样本转换成等级，无需考察样本规模及总体分布特性，具有快捷、稳健的特点。首先，把数列x={x1，x2，…，xn}按升序或降序排列，得到排序数列a={a1，a2，…，an}，将x内各元素xi在数列a中的位置记为ri，称其为元素xi的秩次，从而得到秩次数列r。将另一数列y={y1，y2，…，yn}按同样方式排列，得到排序数列b={b1，b2，…，bn}，继而得到y对应的秩次数列s。将数列r和s内每个元素对应地相减，得到秩次差数列d={d1，d2，…，dn}。则SRCC计算表达式如下：

(18)

式中：ρ为SRCC值；n为数列点数，对应采样点数。

式(18)中，分子为2个序列的误差和，反映2个变量之间的差异；分母为与序列长度相关的1个常数。

2.3 具体实现流程

通过研究发现，SSD算法需人为设置奇异谱分量个数K。若K设置得过小，信号未能分解完全，蕴含敏感特征的分量无法被分离，故障信息将被掩盖；若K设置得过大，则易出现虚假分量，同时运算量加大。针对该问题，本文提出1种自适应奇异谱分解方法，采用合成峭度与SRCC作为联合判据，可实现奇异谱分量个数K的自适应确定。具体过程如下。

首先，初始化分解数量K=2，应用SSD将原始信号分解为若干个SSC分量。计算各SSC分量与原始信号的SRCC，提取最小值，记为ρm1。将ρm1作为停止迭代条件，即判断ρm1是否小于0.1。若小于0.1，即认为通过SSD算法分解产生了与原信号不相关的分量，视为原始信号被过度分解，则输出(K-1)为最佳奇异谱分量个数。

其次，计算各SSC分量的合成峭度，按合成峭度最大原则从各奇异谱分量中剥离出包含敏感特征信息的最佳奇异谱分量SSC-M。计算SSC-M分量与其余各分解分量的SRCC值，提取最大值，记为ρm2。将ρm2作为第二层停止迭代条件，即判断ρm2是否大于0.1。若大于0.1，则认为SSD分解后的信号中已产生与SSC-M相关的分量，视为原始信号被过度分解，则输出(K-1)为最佳奇异谱分量个数。

若ρm1大于0.1且ρm2小于0.1，则K=K+1。重复上述过程，最终可自适应地得到SSD的最佳奇异谱分量个数。奇异谱分量个数自适应选取流程如图1所示。

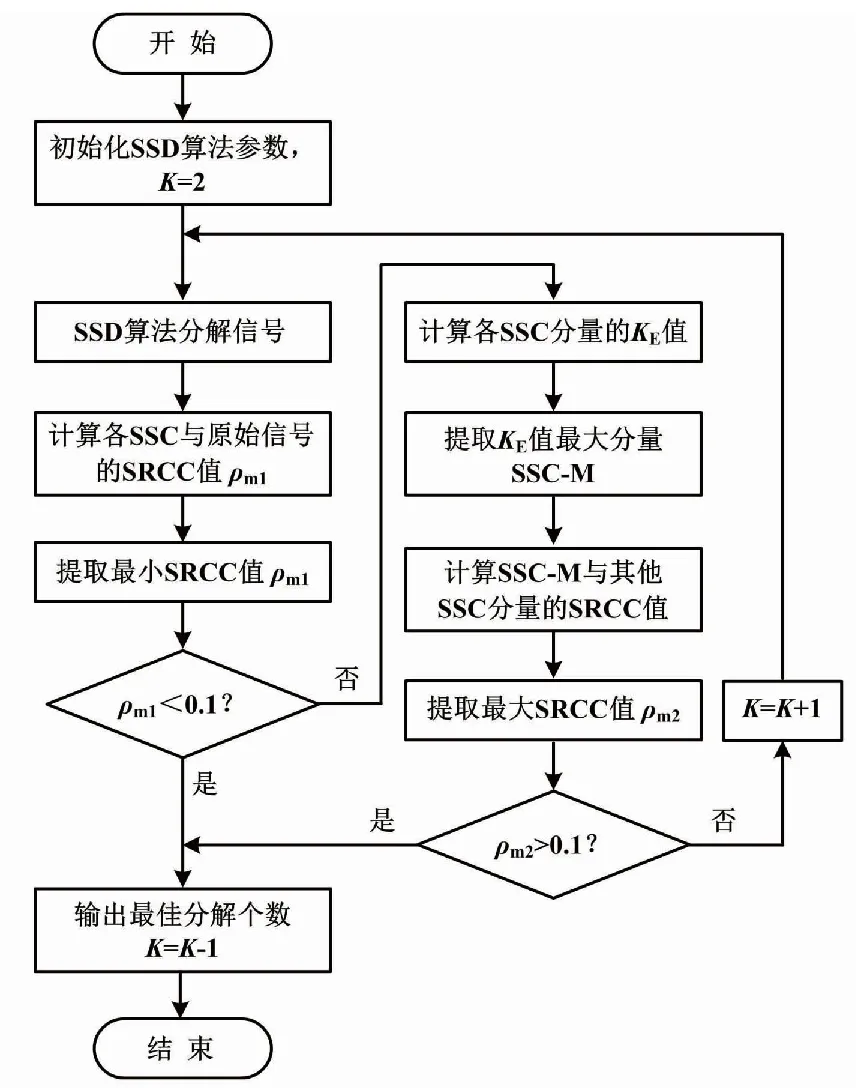
图1 奇异谱分量个数自适应选取流程

3 故障特征提取

基于ASSD-MOMEDA-FWEO的轴承微弱故障特征提取流程如图2所示。

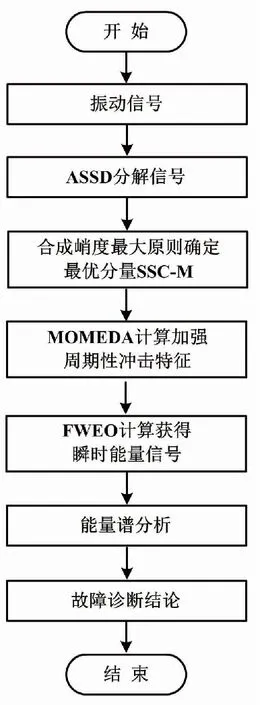
图2 故障特征提取流程

故障特征提取流程具体步骤如下。

①采用ASSD分解原始信号，得到一系列SSC分量。

②按合成峭度最大原则，从ASSD处理结果中筛选出蕴含丰富特征信息的最佳奇异谱分量。

③利用MOMEDA算法对最佳奇异谱分量进行解卷积处理，实现微弱故障特征信息的进一步强化。

④执行FWEO运算，计算所得解卷积信号的瞬时能量并进行傅里叶变换，得到其瞬时能量谱。

⑤从瞬时能量谱中识别峰值明显的频率成分，与理论故障特征频率进行对比，最终判定轴承运行状态。

4 仿真数据分析

为评估本文所提ASSD-MOMEDA-FWEO方法的故障特征辨识能力，采用以下模型[12]对强噪声背景下的滚动轴承内圈故障进行模拟。其中，采样频率为12 kHz。

(19)

式中：s(t)为轴承故障周期性冲击信号；T为故障周期，取0.006 3 s，则故障频率为159.7 Hz;A0为冲击信号幅值，取1；B为衰减系数，取800；fr为转频，取29.5 Hz；fn为局部缺陷冲击所激发的谐振频率，取3 500 Hz；u(t)为单位阶跃函数；n(t)为高斯白噪声，添加噪声后的仿真信号信噪比为-14.8 dB。

仿真信号时域波形及包络谱如图3所示。由图3可知，内圈故障特征频率及其倍频均淹没在强噪声中，表明传统包络方法对该故障仿真信号特征提取失效。

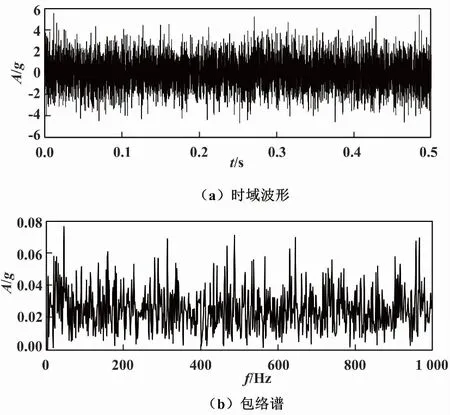
图3 仿真信号时域波形及包络谱

根据ASSD算法实现流程，当K为2～3时，ρm1均大于0.1，且ρm2均小于0.1，因此继续分解；当K=4时，ρm1为0.075 1，小于0.1，因此停止分解，输出最佳奇异谱分量个数为3。

本文算法仿真信号处理结果如图4所示。

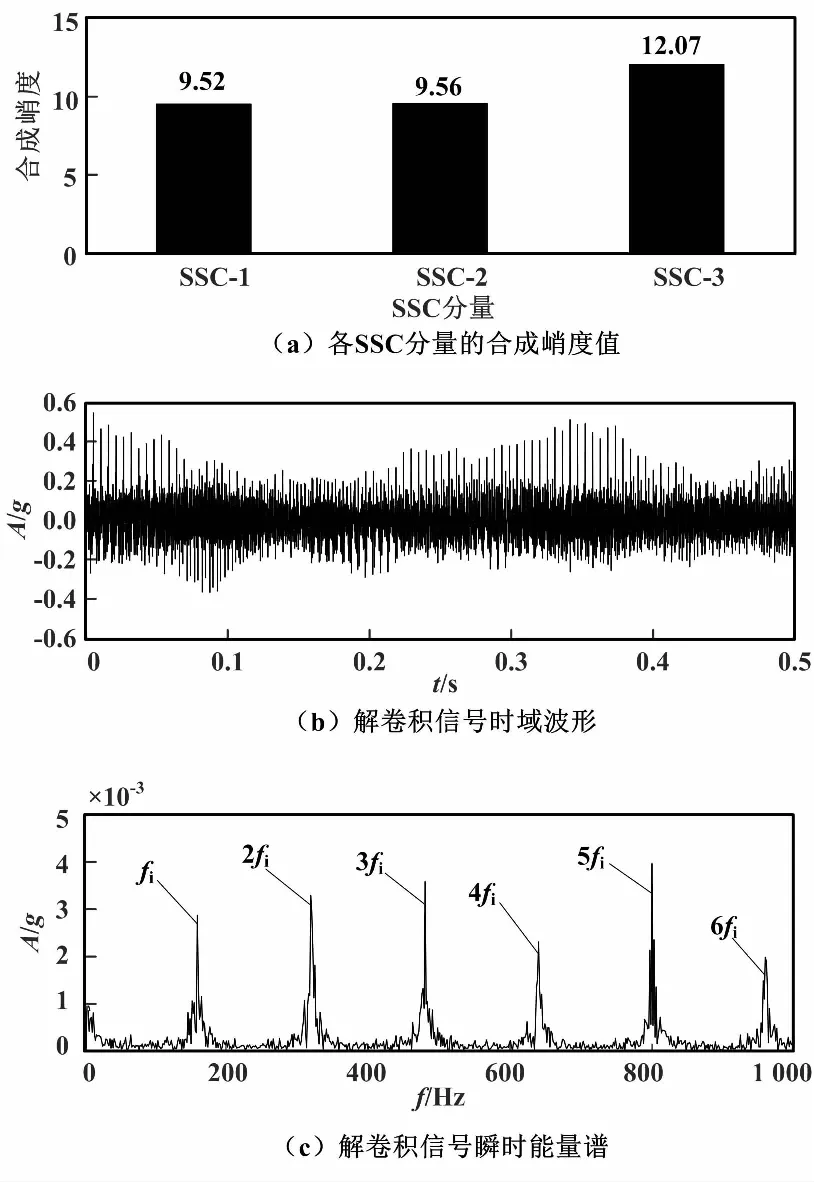
图4 本文算法仿真信号处理结果

原始仿真信号经ASSD处理后，得到3个分量，计算各SSC分量的合成峭度值如图4(a)所示。其中，SSC-3分量合成峭度值最大，将其作为最优分量。对SSC-3分量进行MOMEDA处理后的解卷积信号时域波形如图4(b)所示，周期性脉冲成分得以加强，通过FWEO进一步追踪解卷积信号的瞬时能量，并计算得到解卷积信号瞬时能量谱如图4(c)所示。其中，故障特征频率基频～6倍频成分均清晰可辨。

EMD算法仿真信号处理结果如图5所示。

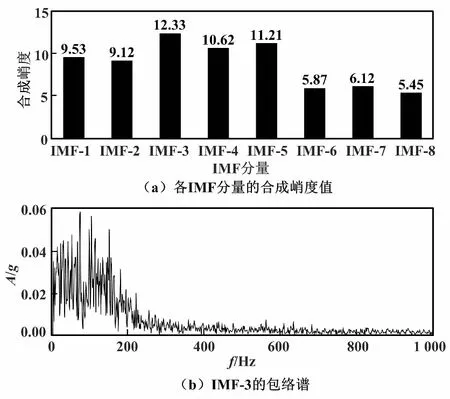
图5 EMD算法仿真信号处理结果

为验证本文方法在强噪声环境下故障信息剥离及周期性冲击特征增强的优势，采用经验模态分解(empirical mode decomposition,EMD)方法进行对比研究。仿真信号经过EMD处理后得到8个IMF分量，计算各IMF分量的合成峭度值，如图5(a)所示。其中，IMF-3分量的合成峭度值最大，因此将IMF-3作为最优分量。图5(b)为IMF-3的包络谱，无法提取出故障特征频率。

5 试验数据分析

为进一步探究本文方法在实际工况下的有效性，采用美国凯斯西储大学轴承数据中心的试验数据进行分析。滚动轴承故障模拟试验台包括电机、扭矩传感器、功率计和控制元件4大部分。驱动端轴承型号为SKF6205，轴承节径为39.04 mm，滚动体直径为7.94 mm，滚动体为9个，接触角为0°。试验轴承故障通过电火花在内、外圈植入，故障特征频率计算表达式为：

(20)

(21)

5.1 外圈故障信号分析

外圈故障试验信号时域波形与包络谱如图6所示。

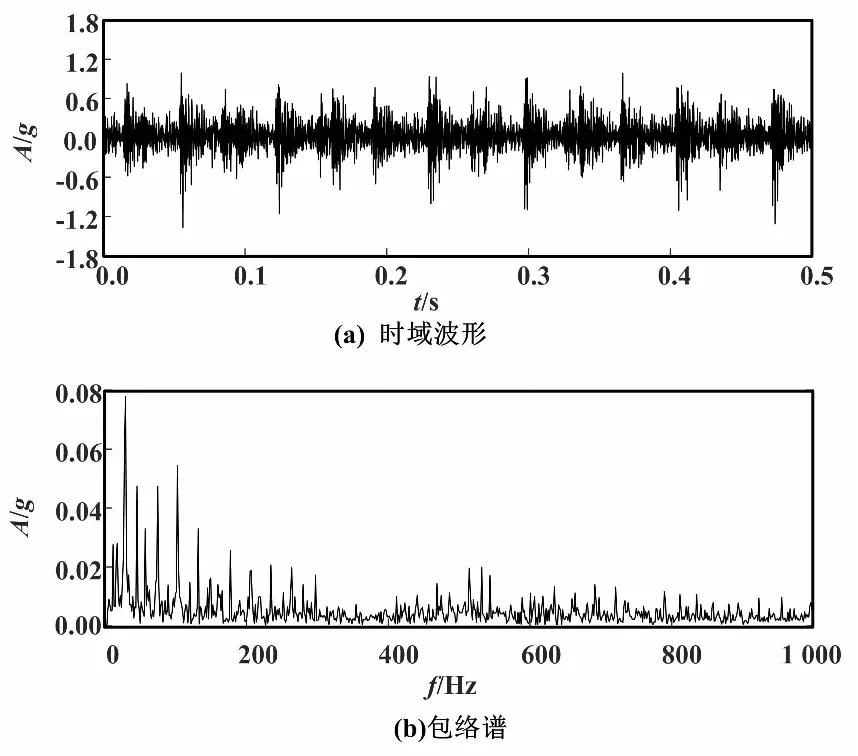
图6 外圈故障试验信号时域波形与包络谱

选取电机驱动端处轴承外圈点蚀直径为0.533 4 mm的故障数据进行分析：试验采样频率为12 kHz，电机转速为1 718 r/min，转频fr=28.63 Hz。根据式(20)计算出外圈理论故障特征频率f0=102.6 Hz。由图6可知，外圈故障特征频率基频可被识别，但谱图中无关干扰频率成分过多，并且特征频率的倍频均无法识别。整体来看，传统包络谱分析方法诊断效果不佳。

根据ASSD算法实现流程，当K为2、3时，ρm1均大于0.1，且ρm2均小于0.1，继续分解；当K=4时，ρm1为0.245 3，大于0.1，但ρm2为0.162 4，大于0.1，停止分解。因此，可确定最佳奇异谱分量个数为3。

本文算法外圈故障信号处理结果如图7所示。外圈故障试验信号经过ASSD处理得到3个分量。经计算，得到各SSC分量的合成峭度值如图7(a)所示，选择合成峭度最大的SSC-2为最优分量。对SSC-2分量进行MOMEDA解卷积处理，解卷积信号时域波形如图7(b)所示。其周期性冲击成分得以明显加强。进一步执行FWEO获得解卷积信号的瞬时能量，通过频域变换得到的解卷积信号瞬时能量谱，如图7(c)所示。外圈故障特征频率的基频～9倍频成分均清晰呈现，分析效果与图6(b)相比显著提升。

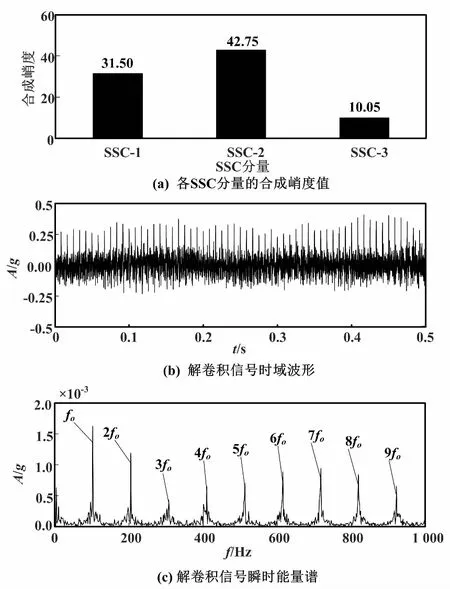
图7 本文算法外圈故障信号处理结果

5.2 内圈故障信号分析

内圈故障试验信号时域波形与包络谱如图8所示。

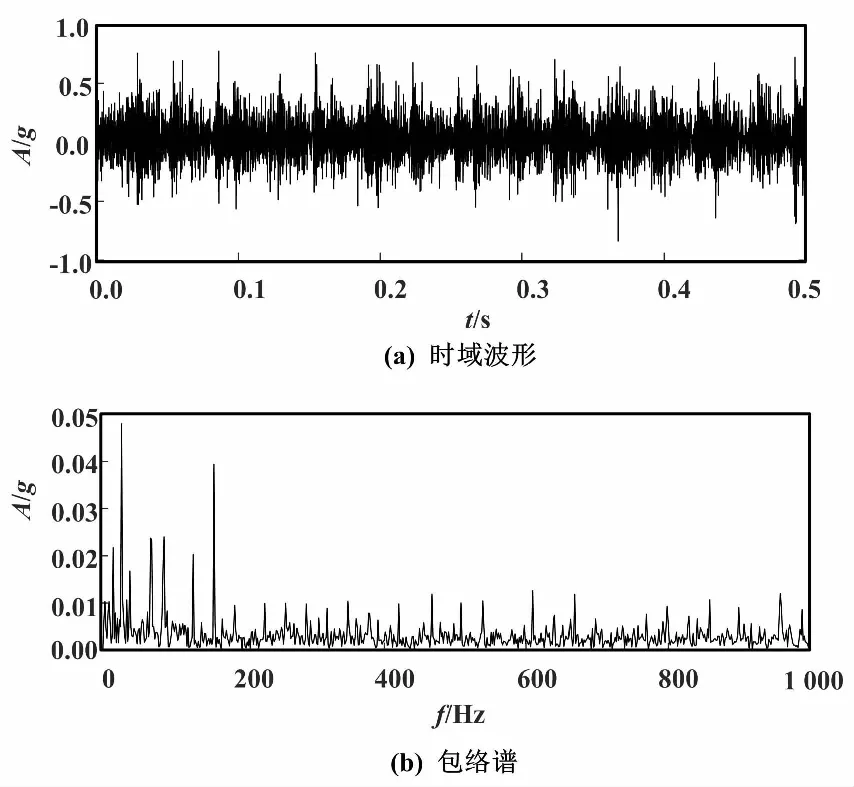
图8 内圈故障试验信号时域波形与包络谱

选取电机驱动端处轴承点蚀直径为0.533 4 mm的内圈故障数据，电机转速为1 772 r/min，转频fr=29.53 Hz，根据式(21)计算得到内圈理论故障特征频率fi=159.9 Hz。图8所示的谱图中仅可识别出内圈故障特征频率的基频成分，其倍频成分均无法辨识，分析效果存在很大提升空间。

利用ASSD算法对该信号进行处理。当K为2～4时，ρm1均大于0.1，且ρm2均小于0.1，因此继续分解；当K=5时，ρm1为0.109 6，大于0.1，但ρm2为0.269 0，大于0.1，停止分解。因此，可确定最佳奇异谱分量个数为4。

本文算法内圈故障信号处理结果如图9所示。

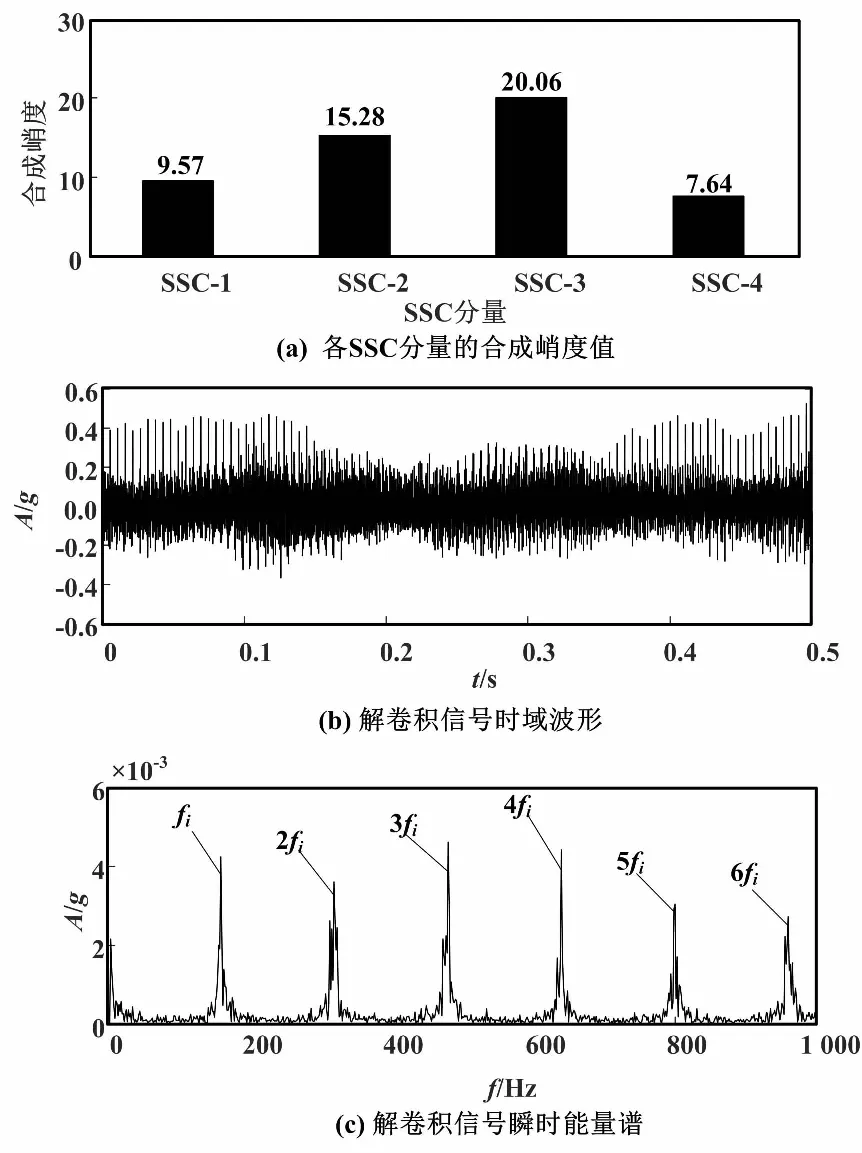
图9 本文算法内圈故障信号处理结果

内圈故障试验信号经过分解处理得到4个SSC分量，各SSC分量的合成峭度值如图9(a)所示。其中，SSC-3合成峭度值最大。因此，将SSC-3作为最优分量作进一步解卷积处理，所得解卷积信号时域波形如图9(b)所示，最终所得解卷积信号瞬时能量谱如图9(c)所示。其中，内圈故障特征频率基频及其倍频成分均被有效提取出来，据此可实现轴承状态准确判定。

6 结论

针对轴承微弱损伤难以准确识别的问题，本文提出了基于ASSD-MOMEDA-FWEO的滚动轴承故障诊断方法，并通过仿真及试验信号进行验证，总结如下。

①采用合成峭度及斯皮尔曼等级相关系数，可自适应确定SSD的奇异谱分量个数，实现原始信号的合理分解。通过合成峭度指标可直接从ASSD分解结果中筛选出包含丰富故障信息的最优分量，有利于后续分析处理进程。

②MOMEDA算法能够有效增强被噪声淹没的周期性冲击成分。将其与FWEO算法进行融合，作为后处理策略，可在强背景噪声干扰下进一步强化、放大微弱故障特征，有助于实现轴承故障的精确诊断。