关于混合图H-秩的一个注记

朱佳敏，李双东，2

（1．安徽大学 数学科学学院，安徽 合肥 230601；2．安徽大学江淮学院，安徽 合肥 230031）

1 预备知识

引理1.1

（1）如果

v

不在

G

的任何圈上，则（2）如果

v

在

G

的一个圈上，则

c

(

G

-

v

)≤

c

(

G

)-1；（3）如果

G

中包含顶点相交的圈，则存在位于相交圈上的顶点

v

，满足

c

(

G

-

v

)≤

c

(

G

)-2；（4）如果

G

中的圈两两不交，则

c

(

G

)等于

G

中圈的个数。

引理1.2

引理1.3

引理1.4

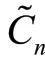
定义1.5

设

G

是含悬挂点的简单图，将

G

中的悬挂点及其邻点一起删除的操作称为 -

δ

变换。设

G

是圈互不相交的简单图。对

G

连续实施

δ

-变换，直到得到的子图不含悬挂点，称该子图是

G

的一个重要子图。把

G

中的每个圈都收缩成一个新的顶点，所得不含圈的图记作

T

，所有由圈收缩所得顶点构成的集合记作

W

。将

G

中所有的圈和与这些圈上顶点相关联的边删除，所得不含圈的图记作[

T

]。

引理1.6

引理1.7

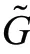
定理1.8

定理1.9

（1）

G

中任意两个圈均没有公共顶点；

（3）

m

(

T

)=

m

([

T

])，即存在

T

的一个最大匹配

M

，使得

M

不覆盖

W

中的点。

引理1.10

注：由上述引理可知，存在H-秩为2

m

(

G

)- 2

c

(

G

), 2

m

(

G

)- 2

c

(

G

)+ 2, 2

m

(

G

)+

c

(

G

)的单圈混合图，不存在H-秩为2

m

(

G

)- 2

c

(

G

)+1的单圈混合图。

2 主要结果

对于图

G

的悬挂点，如果其邻点不在

G

的圈上，则称该悬挂点是类型1的；否则，称该悬挂点是类型2的。

引理2.1

（1）如果

u

是类型1的，则

（2）如果

u

是类型2的，则

证明

（2）如果悬挂点

u

是类型2的，则由引理1.1（2），

由引理1.6，

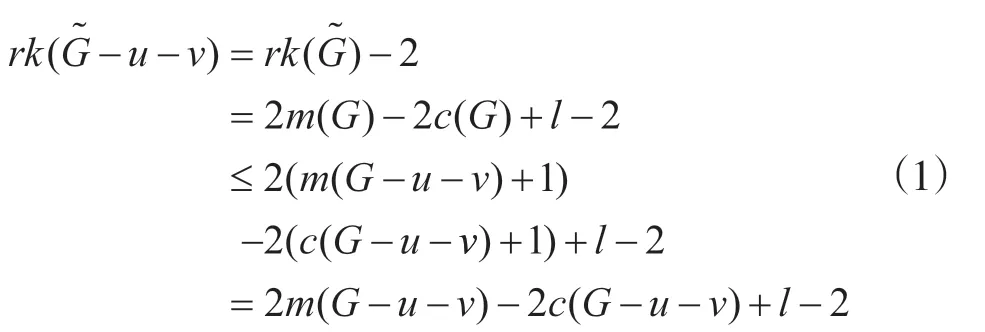
（1）式与定理1.9矛盾，命题得证。

满足()

cG

k

= 的连通简单图称为k-圈图。设

G

是-

k

圈图，

G

不含悬挂点的k-圈子图称为

G

的基。习惯上，2-圈图也称为双圈图。不难发现，双圈图有两种类型的基：

D

(

p

, ℓ,

q

)和

θ

(

r

,

s

,

t

)，如图1所示。设

C

和

C

是两个顶点不相交的圈，路

P

=

v

v

…

v

，

u

∈

V

(

C

)，

v

∈

V

(

C

)。

D

(

p

, ℓ,

q

)是分别将 和

v

粘合成同一个顶点，

v

和

v

粘合成同一个顶点所得的图。

θ

(

r

,

s

,

t

)是将三条内部不相交的路

P

，

P

和

P

的起点和终点分别粘合所得的图。同样不难发现，3-圈图有8种不同类型的基，记作

T

,...,

T

，如图2所示。

图1 双圈图的基

图2 3-圈图的基

例2.2

引理2.3

情形1

子情形1.2 c()≥3

如果在

G

的圈上存在一点

x

，满足

x

∉

V

(

G

[

C

,

C

])，则

G

-

x

包含两个顶点相交的圈

C

和

C

，不满足定理1.9的条件（1）。否则，

G

中的每个圈都是

G

[

C

,

C

]的子图。这意味着

G

[

C

,

C

]包含3-圈图的基

T

(

j

= 5,…, 8)（见图2）作为子图。因而，在

G

的圈上一定存在一个顶点

x

，使得

G

x

- 中有两个顶点相交的圈，不满足定理1.9的条件（1），该情形得证。

情形2

情形3

易见，

E

(

T

)≠∅；否则

G

是由顶点互不相交的圈和孤立点构成，

m

(

T

=

m

([

T

])=0，矛盾。进一步地，可以断言：

T

的每个最大匹配至少覆盖一个悬挂点。否则，

T

的直径路中一定包含一条

M

-增广路，与引理1.7矛盾。注意到，

G

不含悬挂点，则

T

的悬挂点在

G

中对应一个悬挂圈，记其中一个悬挂圈为

C

，记

C

上度为3的顶点为

v

。

子情形3.1

子情形3.2

定理2.4

证明

（2）式与（3）式矛盾，因 此 - 2

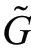
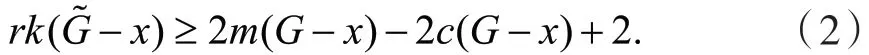
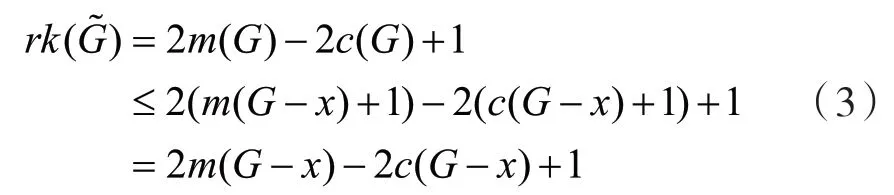
c

(

G

)+1，命题得证。

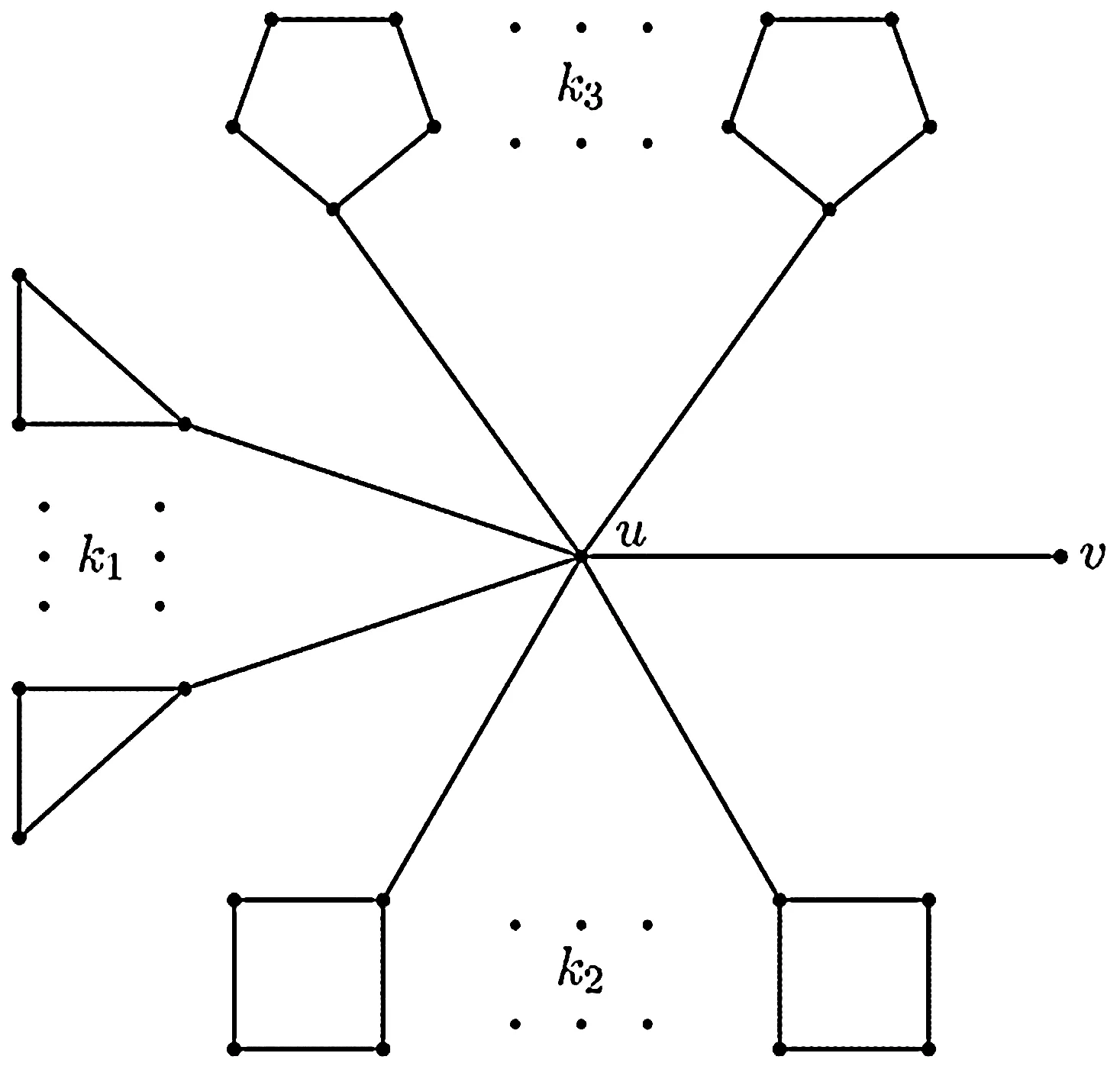
图3

定理2.5

因为

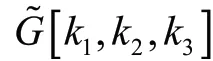
k

,

k

,

k

是非负整数，令

k

=

k

+

k

+

k

，，

l

= 3

k

+2

k

，则

l

可以取[ 0,3

k

]中除1之外的任意整数，命题得证。