基于声发射技术的早龄期扰动对混凝土力学性能影响分析

张长江，徐佰顺，赵志蒙，倪天蒙，刘 斌

(1.内蒙古大学交通学院，呼和浩特 010070；2.内蒙古自治区桥梁检测与维修加固工程技术研究中心，呼和浩特 010070)

0 引 言

桥梁是交通基础设施的关键枢纽，由于恶劣的工作环境以及不断增加的交通量，大部分桥梁性能都会有一定程度的下降，危桥的数量正逐年增多，需要及时补强加固。桥梁加固一般采用封闭道路施工，这会对流量大的路段造成很大交通压力[1]。若在开放交通条件下进行桥梁加固，车辆与桥梁耦合作用产生的扰动将会对新浇筑混凝土产生一定的影响，因此研究早龄期扰动对混凝土的影响具有重要意义。

混凝土作为桥梁的主要建筑材料，其性能不仅取决于原材料和结构形式，更取决于施工质量[2]。研究[4-5]表明，混凝土砂浆-骨料界面过渡区孔隙率和渗透性高于砂浆基体，而弹性模量和强度却低于砂浆基体[3]，由于骨料强度较大，因此混凝土强度主要由界面过渡区的强度决定。混凝土在终凝前，水泥浆体部分硬化，初步形成内聚力，但此时界面强度较低，内部黏聚结构未完全形成，对外界振动较为敏感[6]，因此混凝土终凝前应避免受到振动，以免对混凝土内部结构造成损坏[7]。潘慧敏等[8-10]发现凝结中期扰动对混凝土损伤较大，临近终凝时混凝土抗扰性提高；何欢等[11]发现不同扰动参数对混凝土性能影响不同，并且扰动大多通过改变混凝土内部孔隙比例进而影响混凝土力学性能；Kwan等[12]研究发现振幅大于3 mm时，混凝土内部裂纹宽度较大。声发射(acoustic emission，AE)作为一种新型无损检测技术被广泛应用于混凝土材料动态损伤的研究中[13]，通过声发射传感器可以识别和定位材料中由任何应力源引起的微观和宏观裂纹[14]，根据不同的声发射参数(如幅值、能量、上升时间等)可以表征混凝土内部的损伤情况[15-17]。

现有研究中关于早龄期扰动对混凝土力学性能的影响研究较少，且大多以宏观力学性能作为评价指标，缺乏不同凝结时间和扰动机制对混凝土强度和损伤程度影响的具体研究。本文在上述研究的基础上，采用室内振动台提供扰动，在凝结初期和中期分别选择3种扰动机制进行试验，以抗压强度作为混凝土力学性能的评价指标，并利用声发射对扰动后混凝土的损伤机理进行分析，通过不同的声发射参数表征混凝土损伤劣化程度，为早龄期受扰动混凝土的性能研究提供重要依据。

1 实 验

1.1 原材料和配合比

混凝土强度等级为C40，胶凝材料采用P·O 42.5普通硅酸盐水泥，其性能指标如表1所示。细集料采用本地沙场生产的河沙，粒径范围为0.15～4.75 mm，粗集料采用4.75～9.5 mm、9.5～13.2 mm、13.2～16 mm、16～19 mm、19～26.5 mm五档机械破碎的玄武岩碎石，其质量比为0.30 ∶0.19 ∶0.12 ∶0.12 ∶0.27，骨料使用前进行严格的筛分、清洗和烘干，骨料物理力学性能见表2、表3。混凝土水灰比为0.43，为了确保混凝土的和易性，混凝土的坍落度控制在(180±20)mm范围内，混凝土材料用量如表4所示。

表1 水泥物理力学性能Table 1 Physical and mechanical properties of cement

表2 细集料物理力学性能Table 2 Physical and mechanical properties of fine aggregate

表3 粗集料物理力学性能Table 3 Physical and mechanical properties of coarse aggregate

表4 混凝土材料用量Table 4 Concrete material consumption

1.2 试验方案

试件尺寸为150 mm×150 mm×150 mm，为测试扰动后混凝土试件的力学性能，配合比设计完成后，先测试混凝土的凝结时间。混凝土凝结时间测定参照《普通混凝土拌合物性能试验方法标准》(GB/T 50080—2016)实施，根据单位面积贯入阻力3.5 MPa和28.0 MPa,将混凝土的凝结时间分为凝结初期、凝结中期及凝结后期三个阶段，试验测得新浇筑混凝土初凝时间和终凝时间分别为7.5 h和9.5 h，因此混凝土加水搅拌后0～7.5 h为凝结初期，7.5～9.5 h为凝结中期，9.5～24.0 h为凝结后期。

混凝土拌制完成后，将混凝土按四分法取料浇筑试件，浇筑过程中利用捣棒进行插捣，确保试件密实。由于本试验主要影响因素为扰动参数，因此试件浇筑完成后不进行振动台振捣。已有研究[6-7]表明，新浇筑混凝土在终凝前受到扰动对其性能影响最大，因此本试验的扰动时间为凝结初期及凝结中期。桥梁固有振动频率约为4 Hz，标准振动幅度为1～3 mm[18]，考虑到不同交通量条件下车桥耦合振动频率和幅度会有所变化，因此制作7组试件，每组制作3个平行试件。第一组为基准组，不进行扰动，记为0-0；其他六组试件分别选择凝结初期及凝结中期进行扰动，扰动机制为2 Hz、3 mm，4 Hz、3 mm和4 Hz、5 mm，分别记为C2-3、C4-3、C4-5及2-3、4-3、4-5。扰动试验采用加拿大Quanser公司生产的Hexapod六自由度振动台作为振动源，最大荷载为100 kg，振动频率为0～10 Hz，振动幅度为0～10 mm。振动台振动时通过自制模具将试件与振动台刚性连接(见图1)。混凝土试件扰动时间为浇筑后0～9.5 h，试件扰动完成后，从振动台取下并置于标准养护环境(温度(20±2)℃，湿度≥95%)中养护28 d(见图2)。

图1 六自由度振动台Fig.1 Six degrees of freedom shaking table

图2 试件养护Fig.2 Specimens curing diagram

声发射试验与加载试验同时进行，确保数据时间相对应。单轴压缩试验采用TYA-2000电液式混凝土压力试验机，最大荷载2 000 kN。试验开始前，先将试件表面和压力机上下承台表面擦拭干净，随后将试件放置承压板正中心，仪器开动后，控制加载速率为2 kN/s,匀速加载，直至试件破坏。声发射试验采用美国PAC公司生产的Micro II Express八通道声发射系统和DT15I-AST纵波传感器，传感器尺寸为OD 30 mm×H 30 mm,其中 OD为传感器外径，H为高度。门槛值为35 dB，前置放大增益为40 dB，模拟滤波器范围为100～400 kHz，采用其中8个通道进行信息采集。传感器与试件间涂抹真空润滑脂作为耦合剂，并使用夹具将传感器固定在试件表面，确保传感器与试件表面接触良好。试验开始前进行断铅试验，检验传感器及相应系统是否正常工作。声发射试验装置及传感器布置分别如图3、图4所示。

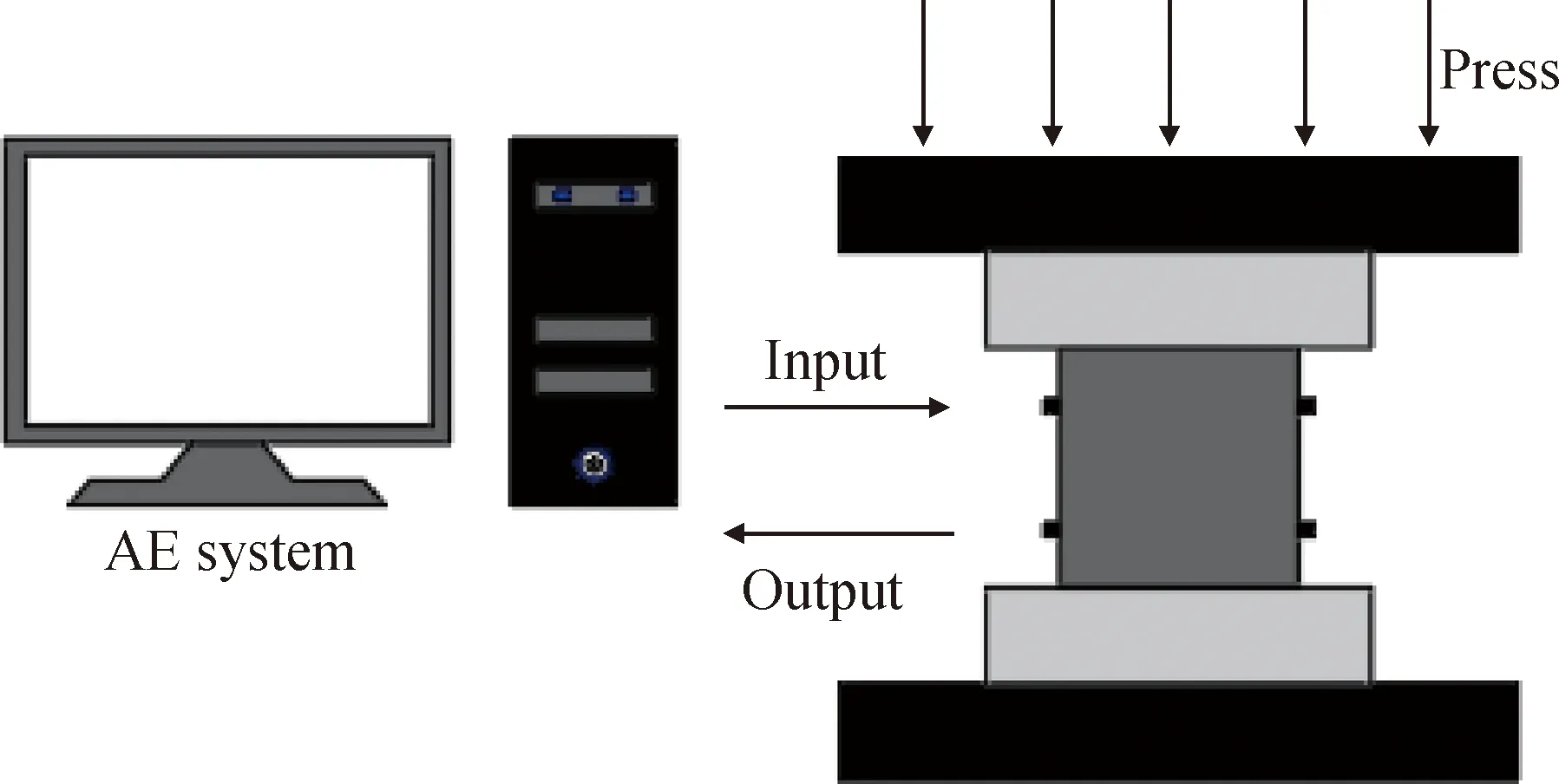
图3 声发射试验装置示意图Fig.3 Schematic diagram of AE test device

图4 声发射传感器布置示意图(单位:mm)Fig.4 AE sensor arrangement diagram (unit:mm)

2 结果与讨论

2.1 抗压强度分析

通过抗压强度试验，得到凝结初期及凝结中期受扰动不同试验组的抗压强度，并通过式(1)计算强度变化率，具体数值见表5。

表5 混凝土抗压强度Table 5 Compressive strength of concrete

(1)

式中：D为强度变化率；fi为各组抗压强度；f0为基准组抗压强度。

图5为强度随频率、幅度变化规律，由图5及表5可知，扰动机制相同时，凝结初期受扰动混凝土的抗压强度增大，而凝结中期受扰动混凝土的抗压强度减小。其中试件0-0强度为45.2 MPa；凝结初期受扰动试件C2-3、C4-3、C4-5强度分别为47.9 MPa、51.0 MPa、49.6 MPa，强度变化率分别为6.0%、12.8%及9.7%；而凝结中期受扰动试件2-3、4-3、4-5强度分别为42.9 MPa、42.0 MPa、40.2 MPa，强度变化率分别为-5.1%、-7.1%及-11.1%。

图5(a)中，扰动幅度为3 mm，扰动频率由2 Hz增加至4 Hz时:凝结初期受扰后试件强度随频率增大而增大，其强度由47.9 MPa增加至51.0 MPa，强度增大6.5%；凝结中期受扰动试件强度随频率增大而减小，其强度由42.9 MPa下降至42.0 MPa，强度减小2.1%。图5(b)中，扰动频率为4 Hz，振动幅度由3 mm增加至5 mm时:试件凝结初期受扰动强度由51.0 MPa减小至49.6 MPa，强度下降3.4%；而凝结中期受扰动强度由42.0 MPa下降至40.2 MPa，强度下降4.3%。

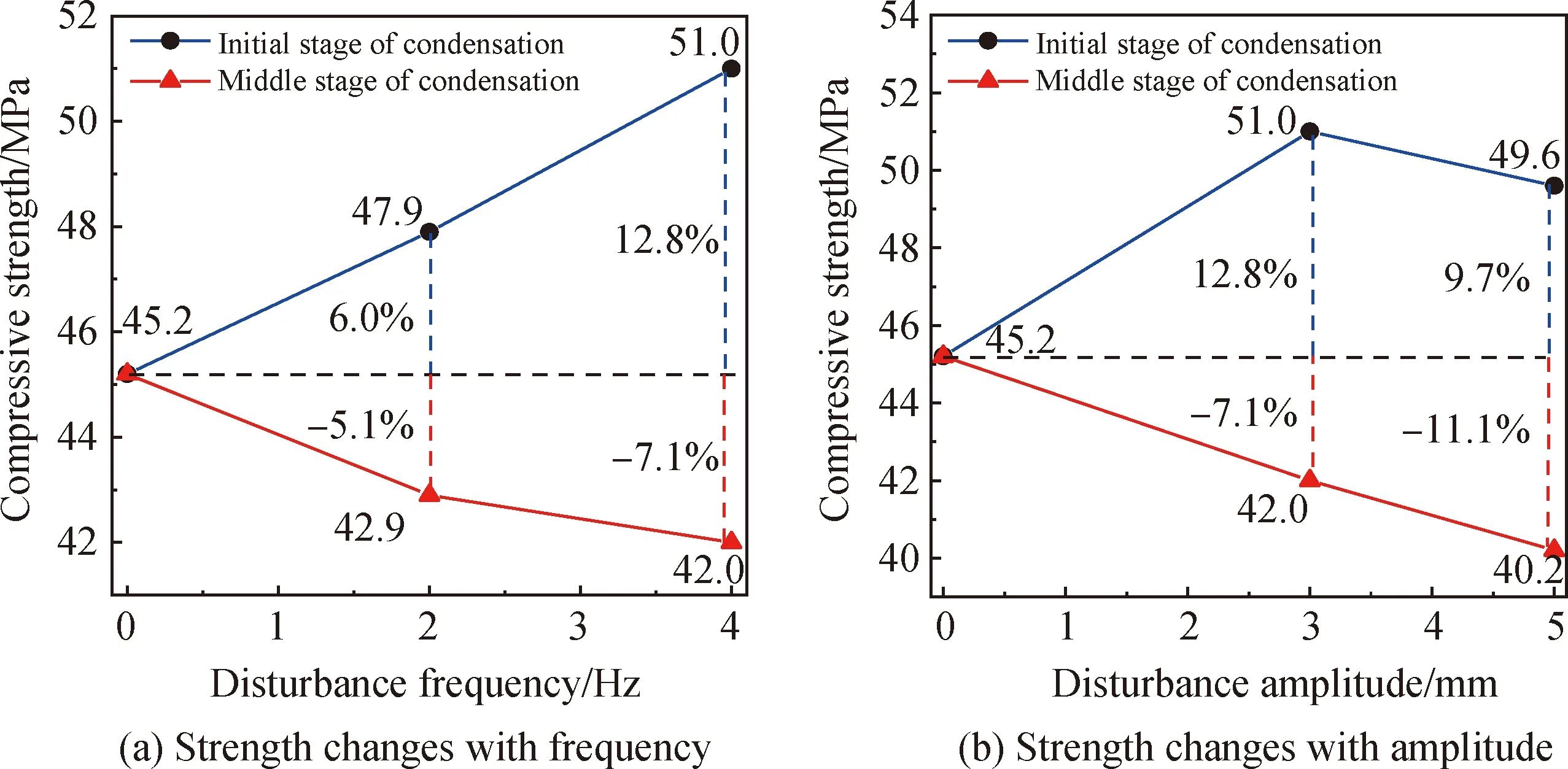
图5 强度随频率、幅度变化规律Fig.5 Variation of strength with frequency and amplitude

上述试验结果表明，早龄期受扰动混凝土强度变化率均大于5%，表明早龄期受扰动对混凝土抗压强度存在较大影响。混凝土密实度、内部细观损伤等因素对混凝土强度影响较大[19]。在扰动频率为0～4 Hz,扰动幅度为3～5 mm时，凝结初期受扰动试件抗压强度增大，且扰动频率增大，试件强度增大，扰动幅度增大，试件强度减小，这是因为混凝土此阶段尚处于流动状态，自愈性较强，扰动对混凝土造成的损伤可以自行恢复，振动频率增大会促进砂浆填充骨料空隙，导致混凝土密实度增大，因此混凝土的强度增大，而振幅增大后骨料与砂浆密度不同，导致材料之间的黏聚力不足以抵抗粗集料下沉，致使粗骨料与砂浆分离，出现离析现象，因此混凝土强度降低；凝结中期受扰动试件抗压强度减小，且扰动频率、幅度越大，试件强度值越小，这是因为凝结中期混凝土已基本失去自愈性，此时扰动会破坏材料内部的初始黏聚结构，骨料与砂浆间的黏聚力降低，因此频率、幅度增加均会导致混凝土强度降低。

2.2 能量-b值分析

声发射参数波形图如图6所示，图中t为时间，v为传感器输出电压。其中：电压门槛值(threshold voltage)可用于选择性拒绝某些声发射信号，只有信号幅值超过电压门槛值时，系统才会记录该信号；幅值(amplitude)指声发射信号波形的最大振幅值，可用于声发射信号的声源鉴别；上升时间(rise time)指信号超过门槛值至最大幅值所经历的时间，可用于噪音鉴别；持续时间(duration time)指信号首次越过门槛值至最后下降至门槛值所经历的时间；声发射能量(acoustic emission energy)指声发射信号波形包络图下面积，反映了信号强度，可用于鉴别信号源的活动特性。

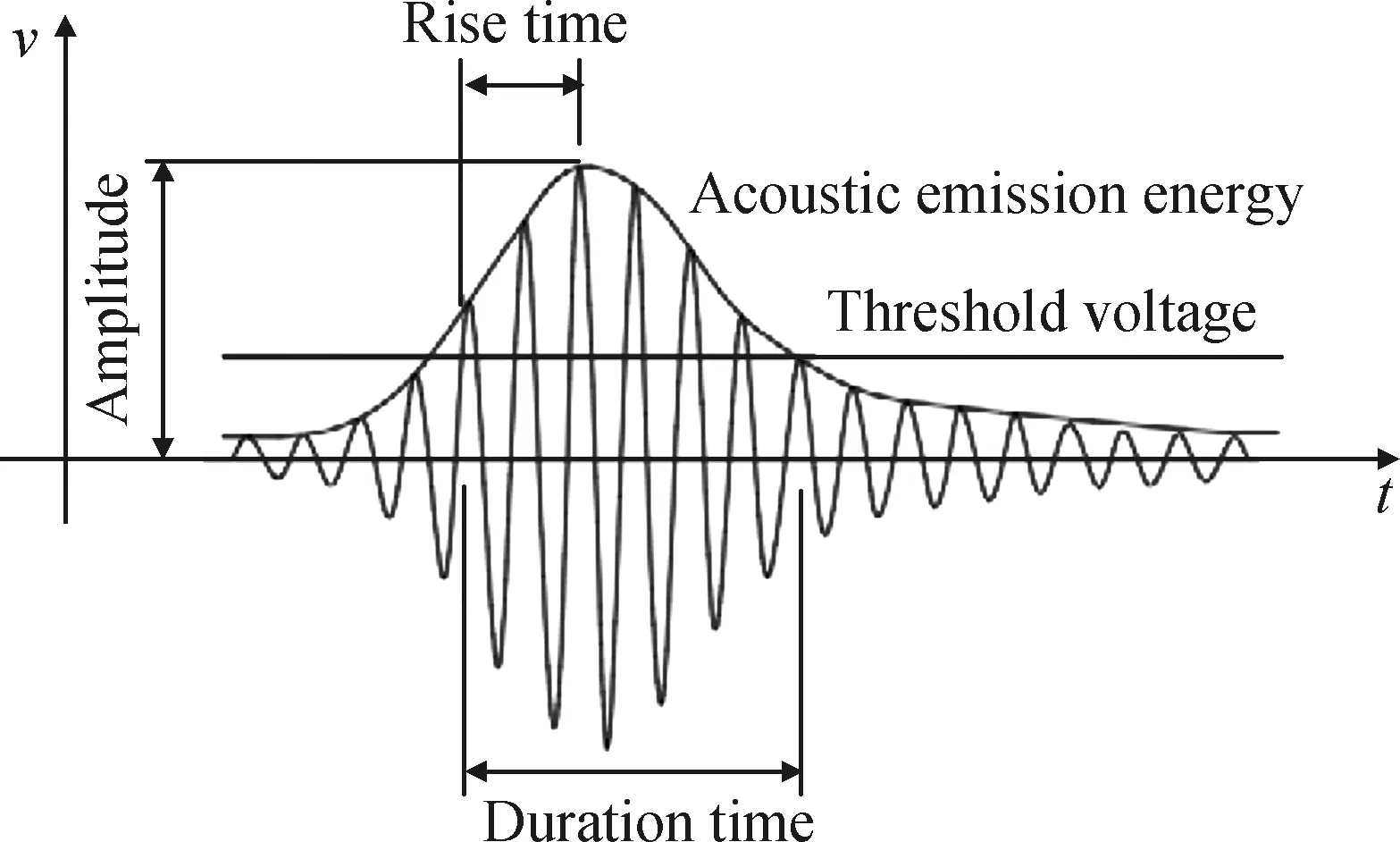
图6 声发射波形参数Fig.6 AE waveform parameters

混凝土材料的组成、性能、配合比等因素导致砂浆与骨料之间的界面存在较多的微裂缝。混凝土破坏主要是由砂浆与骨料黏结面的裂纹扩展引起的，混凝土试件受压过程中，由于砂浆和集料的弹性模量存在差异，在外力作用下，砂浆与骨料变形不一致导致黏结面产生微裂纹，同时砂浆和骨料材料本身在荷载作用下也会产生裂缝。微裂纹的产生、压密和贯通都会释放出弹性应变能。

混凝土断裂可通过声发射幅值分布进行分析。混凝土b值分析方法起源于地震学领域，用于检测地震震级。由于混凝土开裂时产生的弹性波与地震波的性质相似，因此可以通过b值分析法监测单轴受压时混凝土内部材料的开裂情况[20]，其函数表达式为

(2)

式中：AdB代表声发射信号的幅值，dB；a为沿lgN轴的截距；N为声发射事件点的数量;b为拟合曲线斜率。

本文选择计算方法简单且方便的最小二乘法计算b值，每组数据选取1 000个声发射事件，并以100个事件进行取样计算，从而得到b值随应力的变化规律。

由式(2)可知，b值与声发射信号幅值AdB成反比，微裂纹产生时，声发射信号幅值较低，b值较高；而宏观裂纹产生时，声发射信号幅值较高，b值较低，因此可以通过b值变化趋势判断加载过程中混凝土内部微观和宏观裂纹的变化。图7为试件加载过程中声发射b值和能量随应力的变化趋势，图中应力均为相对应力，即各时刻应力σ与峰值应力σmax的比值。

图7中，混凝土试件声发射能量和b值曲线变化规律与混凝土材料的损伤发展密切相关，可将混凝土试件加载过程大致分为三个阶段：弹性压密阶段、稳定发展阶段和塑性破坏阶段。弹性压密阶段声发射能量的释放主要是由于初始加载时试件与承压板的摩擦作用及压力作用下试件内部原始空洞变形，因此声发射能量曲线上升较快，此阶段为微裂纹产生阶段，声发射信号幅值较低，b值曲线整体呈上升趋势；稳定发展阶段，微裂纹产生较少，原有裂纹平稳发展且未相互连通，此阶段能量释放较少，b值较低且曲线较为平缓；进入塑性破坏阶段后，骨料与砂浆结合面处微裂纹快速发展并相互连通，贯穿骨料并延伸至试件表面产生宏观裂缝，此时可以观察到声发射能量释放迅速增大，b值曲线大幅下降，且随着荷载增加，伴有轻微响声，内部裂纹扩展至表面，试件即将达到峰值荷载。

分析图7可知，不同凝结时间进行扰动对混凝土试件产生的影响不同。试件0-0累计声发射能量为42 026 dB·μs；凝结初期扰动后，试件累计声发射能量增大，其中试件C2-3、C4-3、C4-5破坏时累计声发射能量分别为48 640 dB·μs、72 405 dB·μs、55 841 dB·μs；凝结中期扰动后，试件累计声发射能量减小，其中试件2-3、4-3、4-5累计声发射能量分别为38 080 dB·μs、32 737 dB·μs、29 437 dB·μs。扰动幅度为3 mm，振动频率由2 Hz增加至4 Hz时，凝结初期振动试件累积能量增大，而凝结中期扰动试件相反；振动频率为4 Hz，振动幅度由3 mm增加至5 mm时，凝结初期和中期扰动试件规律相同，均表现为累积能量减小，这说明凝结初期扰动后，频率增大，试件内部初始微裂纹较少，振幅增大后，初始微裂纹数量增多，但仍小于基准试件；凝结中期扰动后，试件初始微裂纹数量增多，且扰动频率和幅度越大，试件初始微裂纹数量越多。

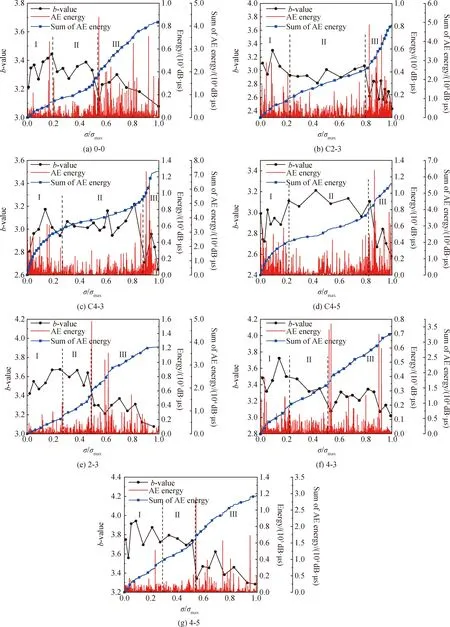
图7 能量-b值曲线Fig.7 Energy-b-value curves

出现这种现象是因为:凝结初期试件扰动后，内部结构致密，原生微裂纹减少，出现微裂纹时产生的声发射信号幅值较大，裂纹产生、扩展及事件破坏产生声发射能量较多，因此试件破坏时累计能量值较高，其中试件C4-3累积声发射能量最大，说明试件C4-3初始损伤最小；凝结中期扰动后，试件内部原生裂纹较多，出现微裂纹时产生的声发射信号幅值较小，内部裂纹产生和试件破坏产生声发射能量减少，累积能量值较低，其中试件4-5累积声发射能量最小，说明试件初始损伤最大。

2.3 参数关联分析

声发射参数的关联分析是将任意两个声发射特征参数联系起来做关联图，关联图的横纵坐标分别代表不同的参数，图上的每一个数据点则表示一个声发射事件。通常选择RA-AF关联分析来分析混凝土的破坏形态，其中RA定义为上升时间与振幅之比，即RA=risetime/amplitude (μs/dB)，AF为平均频率(average frequency)，其定义为振铃计数与持续时间的比值，即AF=counts/duration (kHz)。已有研究表明，剪切破坏和拉伸破坏条件下的RA、AF值存在较大差异:破坏形态为拉伸破坏时，上升时间较短，相关的AF值会更高，RA值较低；而破坏形态为剪切破坏时，由于上升时间和持续时间较长，而平均频率较低，因此RA值较高，而AF值较低[21]。然而，由于两个参数之间的坐标比例并没有清晰的界定标准，无法对试件的裂纹类型进行清晰的划分，因此本文采用一种基于高斯混合模型的概率统计方法，对声发射数据分布特性进行分析，将混凝土在加载过程中的声发射源划分成两类较为显著的群集：剪切和拉伸[22]。

高斯混合模型聚类算法的基本思想就是用多个高斯概率密度分布来精确地量化样本数据，从而使样本数据点处于该种分布下的最大似然概率达到最大值。根据模型数目的不同可以将高斯模型分为单高斯模型和高斯混合模型，单高斯模型即数目为1的高斯混合模型，数据呈正态分布，其概率密度函数[23]如下：

(3)

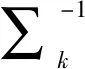
高斯混合模型是由单高斯模型衍化而来的，可以看作是单高斯模型的加权平均和，其概率密度函数p(xi)为：

(4)

式中:s为模型混合数；ωk为权重系数；pk(xi)、N(x;μk;∑k)为第i、k个单一高斯密度函数。

为了计算出最优参数θ，使概率密度值J(θ)达到最大，混合模型的聚类参数估计通常选择最大似然估计法，计算方法如下：

θ=[ωi,μi,∑i],i=1,2,…,n

(5)

(6)

式中：ωi与ωk为权重系数，其和为1；μi和μk是期望。

图8为根据式(3)～(6)计算得到的不同损伤阶段混凝土试件RA-AF关联图，用以判断不同扰动条件下混凝土的破坏形态，图中(1)、(2)、(3)三个阶段分别与前文加载过程的三个阶段相对应，整个加载过程中声发射事件数值如表6所示。

表6 声发射事件点数Table 6 Acoustic emission event points

由图8可知，混凝土试件在不同加载阶段均表现出相同的特征，即拉伸裂缝事件点数较多而剪切裂缝事件点数较少，这说明试件破坏过程以拉伸裂缝为主。此处拉伸裂缝主要是外荷载作用下试件横向膨胀导致微裂纹萌生所产生的事件点，而剪切裂缝指试件加载过程中宏观裂缝相互摩擦产生的事件点。弹性压密阶段，试件声发射事件点大部分为拉伸破坏事件点，说明此阶段混凝土损伤主要为拉伸裂缝；稳定发展阶段，剪切裂缝事件点数量增多，说明此时剪切破坏与拉伸破坏同时产生，但试件损伤仍以拉伸裂缝为主，此时混凝土试件部分微裂纹小范围内相互连通，但并未形成宏观裂缝；进入塑性破坏阶段时，剪切裂缝事件点迅速增多，剪切裂缝事件点多集中在此阶段，此时试件内部微裂纹开始相互贯通，产生宏观裂缝。

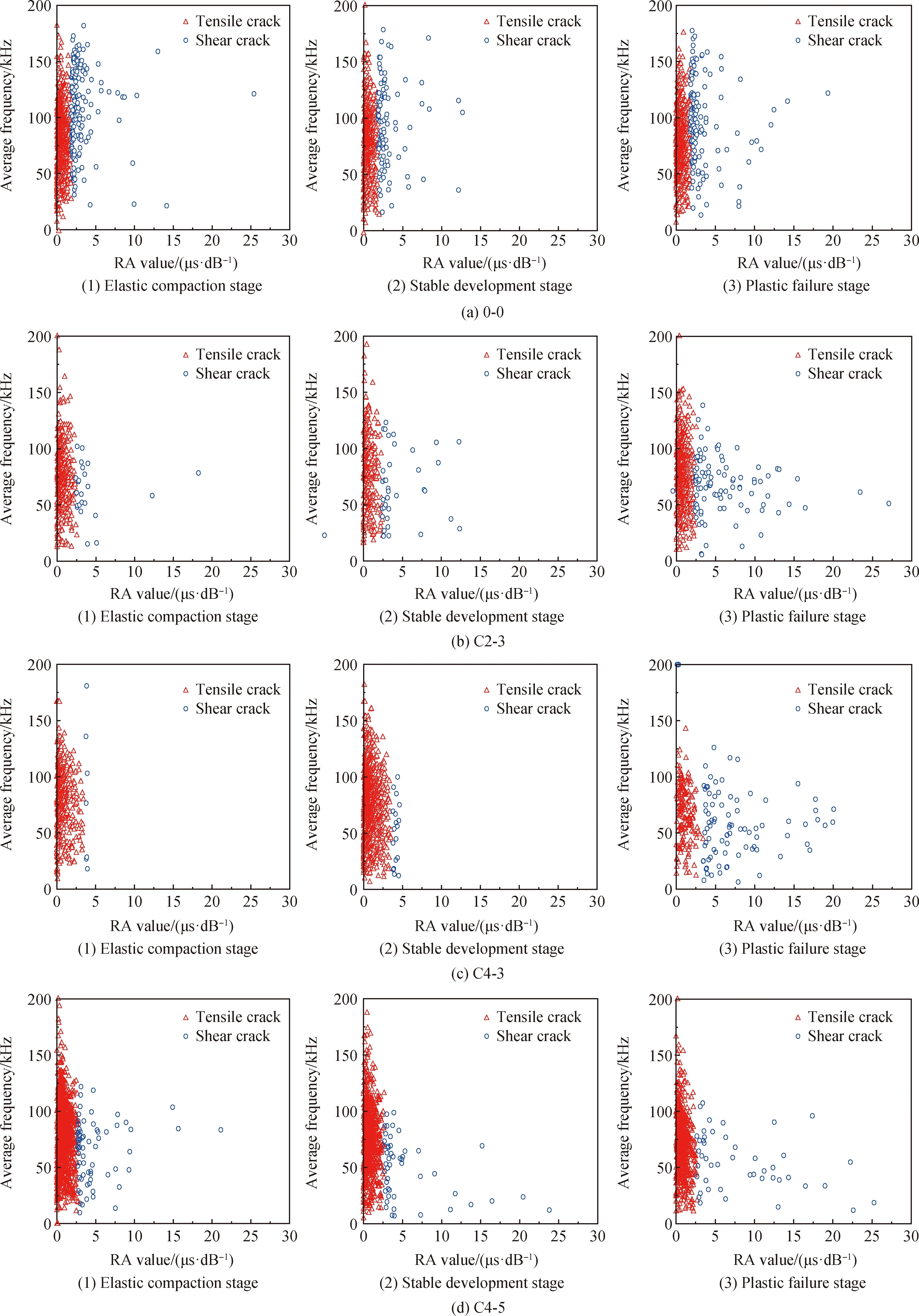
图8 RA-AF关联分析Fig.8 RA-AF correlation diagrams

表6中，振动幅度为3 mm，频率由2 Hz增加至4 Hz时:凝结初期受扰动剪切裂缝事件点数由163减少至114，剪切裂缝所占比率下降3.5个百分点；凝结中期受扰动，试件剪切裂缝事件点数由374增加至559，剪切裂缝所占比率上升6.5个百分点。扰动频率为4 Hz，幅度由3 mm增加至5 mm时，凝结初期、中期受扰动试件规律一致，均表现为剪切裂缝事件点数增大，其中：凝结初期受扰动后剪切裂缝事件点数由114增加至169，剪切裂缝所占比率上升1.4个百分点；凝结中期受扰动，剪切裂缝事件点数由559减少至531，但剪切裂缝所占比率上升5.3个百分点。这说明早龄期扰动对混凝土破坏形态影响较小，试件受扰动后破坏过程仍以拉伸裂缝为主，但对剪切裂缝所占比率影响较大，结合声发射b值及能量分析可知，不同扰动机制下试件初始微裂纹数量不同，初始微裂纹越多，砂浆-骨料界面过渡区强度越低，加载过程中产生宏观裂纹越多，因此试件破坏时剪切裂缝所占比率越大。

2.4 信号强度分析

信号强度分析是对声发射信号的深层次分析，通过参数历史指标HI(historic index)和严重值(severity value)Sr来确定混凝土结构构件的损伤程度[24]。其中历史指标是评估试件加载过程中信号强度变化的指标，计算公式如下：

(7)

式中:M为t时刻的事件数；Soi为原始AE数据中第i个事件的信号强度；K为与试件有关的经验因数。混凝土构件中K值的选取：(a)K=0，M≤50；(b)K=M-30,51≤M≤200;(c)K=0.85M,201≤M≤500;(d)K=M-75,M≥501。

严重值Sr指t时刻内50个最大信号强度的均值，计算公式如下：

(8)

式中：Som为原始AE数据中第m大的信号强度值；R为与材料有关的常数，其选取与M值相关(R=0，M<50；R=50，M≥50)。

历史指标HI和严重值Sr随相对应力的变化如图9所示。

图9 HI和Sr分析图Fig.9 Analysis diagrams of HI and Sr

通过图9(a)、9(b)可以发现，随着荷载增加，Sr曲线的最大值不断增大，说明试件在加载过程中损伤度不断增加，混凝土试件HI每出现一个峰值，与之对应的Sr曲线在该时刻会出现突变，其余时刻曲线较为平缓，说明HI图像的峰值与声发射信号强度相对应，HI值越大，信号强度越大。凝结初期受扰动，试件破坏时Sr减小，而凝结中期受扰动，试件破坏时Sr增大、其中试件0-0的Sr为6.097，试件C2-3、C4-3、C4-5的Sr分别为5.953、5.864、5.920，而试件2-3、4-3、4-5的Sr分别为6.120、6.176、6.256。

事件点的Sr和HI值越大，说明此时试件越接近破坏状态，因此可根据声发射能量-b值分析所划分阶段中每个阶段HI值最大时的声发射信号，找出对应的Sr，并以HI为横坐标，相应的Sr值为纵坐标，绘制信号强度分析图，将信号强度图划分为3个区域，每个区域代表不同的声发射信号严重程度(见图10)。图中区域Ⅰ对应加载过程中的弹性压密阶段，此时HI和Sr值较小，损伤比较轻微；区域Ⅱ对应加载过程中的稳定发展阶段，此时HI和Sr值有所增加，但增幅较小，无较大的损伤产生；区域Ⅲ对应加载过程中的塑性破坏阶段，此阶段HI和Sr值均较大，且事件点均集中在顶部区域，此时声发射信号的损伤源十分严重。因此，较高的Sr值和HI值对应的事件点均位于信号强度图的右上部区域，说明此时损伤较为严重，根据图10顶部区域声发射信号的分布情况，发现试件4-5损伤最严重，而试件C4-3损伤最轻微，规律与前文分析相一致。

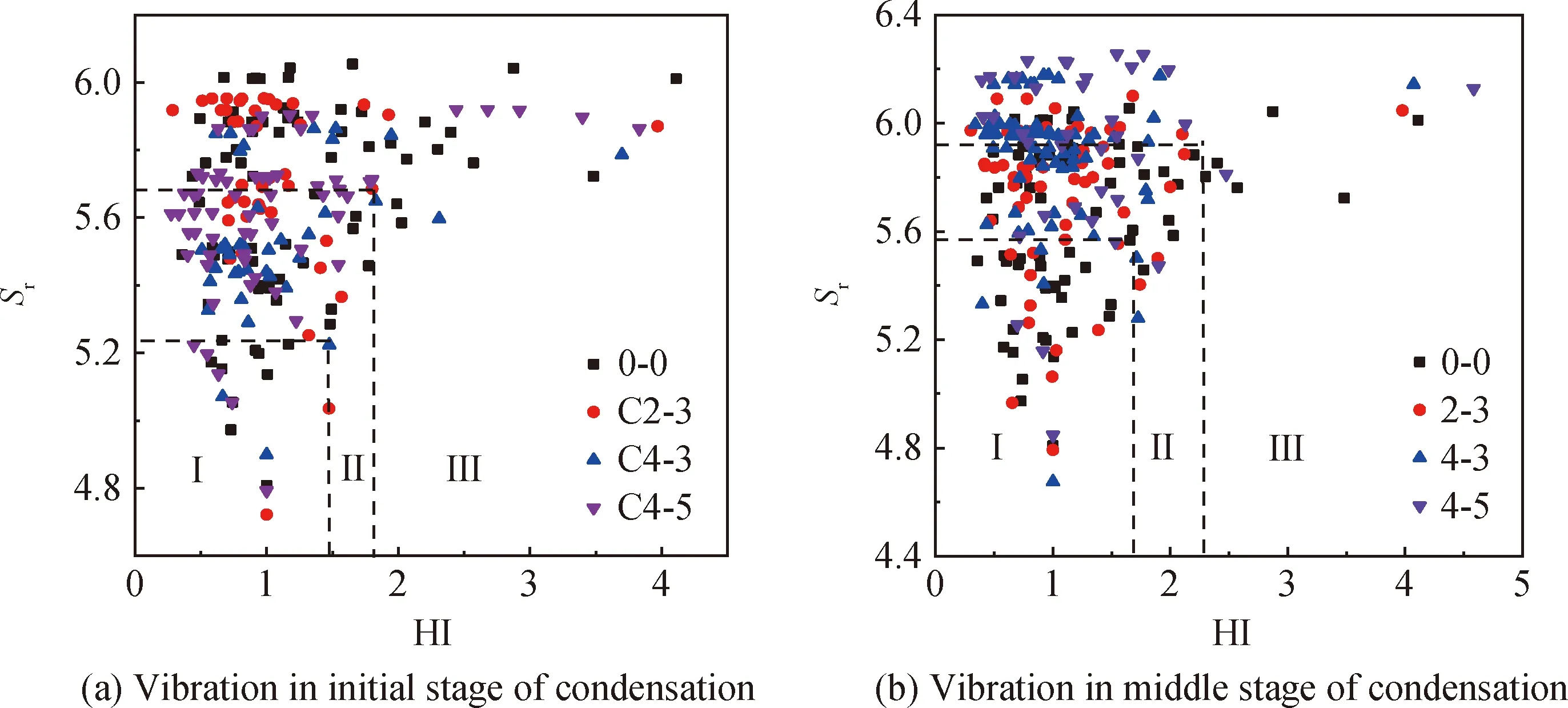
图10 信号强度分析图Fig.10 Analysis diagrams of signal strength

3 结 论

(1)混凝土凝结初期(0～7.5 h)受扰动：扰动频率增大，混凝土抗压强度增大；扰动幅度增大，混凝土抗压强度减小。凝结中期(7.5～9.5 h)受扰动，扰动频率和幅度增大，混凝土抗压强度减小，说明此阶段混凝土抗扰性较差。

(2)通过声发射能量和b值分析将试件损伤过程分为弹性压密阶段、稳定发展阶段、塑性破坏阶段。凝结初期受扰动，扰动频率增大，试件损伤减小，幅度增大，试件损伤增大；凝结中期受扰动，振动频率和幅度增大，试件初始微裂纹增多，损伤越大。

(3)通过高斯混合模型将试件加载过程中的事件点分为剪切破坏和拉伸破坏，发现混凝土试件加载过程以拉伸破坏为主。凝结初期受扰动，振动频率增大，剪切裂缝事件点数所占比率减少，幅度增大，剪切破坏事件点数所占比率增多；凝结中期受扰动，扰动频率和幅度增大，剪切裂缝事件点数所占比率增大。

(4)通过历史指标和严重值分析混凝土试件声发射信号强度，评估试件的损伤：凝结初期受扰动，频率越大，试件损伤越小，幅度越大，试件损伤越大；而凝结中期受扰动，频率和幅度越大，试件损伤越大。