资源受限的飞机总装脉动生产线节拍转换调度建模

陆志强，王浩宇

（同济大学机械与能源工程学院，上海201804）

飞机总装脉动生产线因其产线平稳、生产柔性高，已经广泛应用于大型飞机的装配过程［1］。在飞机总装脉动生产线的生产过程中，装配线被划分为多个资源共享的装配单元，总装过程被拆分为多个作业子集分配到各装配单元上，每个作业子集包含多个作业，这些作业子集可以视为飞机总装项目的子项目。飞机沿生产线方向依次缓慢通过各单元，同时各单元按照装配计划完成装配作业。在一个装配周期内，多架飞机在多个装配单元上同时进行装配。因此，飞机总装脉动生产线的调度问题可抽象为一类多项目调度问题。此外，当一类飞机装配项目生产结束时，需要对生产线上的各类资源进行调整，以适应新的装配项目。在原项目到新项目的转换过程中，原类型飞机不断完工离开生产线，新类型飞机逐渐进入各装配单元，这种2个项目在装配线上共存的时期，称为项目转换期。由于2个项目的资源需求和节拍时间的差异，原有调度计划可能无法正常实施，致使项目延期，因此需要对项目转换期内的装配计划进行调整，重新分配各装配单元对应的作业子集，调整作业时间，制定新的装配计划以优化转换过程，缩短项目工期。目前针对这类问题的研究较少，实际生产时多采用牺牲生产效率、降低装配线速度的方式适应新项目。

为了研究飞机总装脉动生产线的节拍转换过程，提出了基于项目拆分的资源受限项目节拍转换调度问题（RCPTTSP-PS）。RCPTTSP-PS在理论上是一类具有多项目并行调度、复杂约束并且考虑时空多维度的大规模多项目协同调度问题。目前尚没有对RCPTTSP-PS的直接研究，但是对基础的多项目协同调度问题（RCMPSP）的研究已经十分透彻。学界常见的求解RCMPSP的方法有2种，即Goncalves等［2］提出的组合方法和Kurtulus等［3］提出的独立方法，前者是通过虚任务将多项目连接成单项目后求解，后者是对每个项目给出各自的关键路径进行并行求解。Browning等［4］认为第二种方法更加贴近真实情况，将是多项目问题求解的方向。RCMPSP是一个NP难题［5］，无法使用精确算法求解，因此学界多采用启发式算法和元启发算法进行求解。优先级规则是启发式算法的主流，Browning等［4］对20种主流的优先级规则进行了评价，对于不同的项目特性给出了不同优先级规则使用的建议。Wang等［6］和Kurtulus［7］分别引入了随机作业时长和不同的项目延迟惩罚，并分析了相同的优先级规则在不同环境下的求解质量和鲁棒性。元启发算法相较于启发式算法，求解精度更高，但是迭代时间长，适用于静态项目求解。Kim等［8］提出了一种使用模糊逻辑控制器进行参数调整的混合遗传算法以求解RCMPSP；陈俊杰等［9］提出了以蚁群算法为基础的两阶段算法，对考虑柔性资源的RCMPSP效果显著；陈浩杰等［10］使用超启发式遗传规划算法，对多目标RCMPSP进化出最优的优先级规则。

对RCMPSP的扩展问题——基于项目拆分的资源受限项目调度问题（RCPMSP-PS），由陆志强等［11］首先提出并进行了详细阐述，根据项目拆分的特点，设计了双层迭代算法进行求解。朱宏伟等［12］在RCMPSP-PS的基础上，提出了考虑资源转移时间的RCMPSP-PS问题，通过自适应遗传算法有效避免了不合理的资源转移。宗保氏等［13］在RCMPSP-PS的基础上提出了考虑项目拆分的资源投入调度问题，通过遗传算法进行搜索，以优化项目过程的资源投入。在考虑新项目加入调度方面，Chen等［14］考虑了突发订单对生产线的干扰，并对基础计划利用优先级规则进行实时调整；Yassine等［15］对产品开发过程中具有优先级的项目迭代过程进行了建模分析，并利用遗传算法求解，最终给出了可供管理者使用的决策矩阵。Abrantes等［16］对产品开发过程也进行了研究，重点分析产品开发过程中新项目开始时的人力资源再分配问题，通过跨国企业的人力资源管理模式分析，优化管理流程以快速响应产品开发的动态环境。

综上所述，大多数多项目调度研究只考虑了周期内的并行调度，对于有新项目加入的多项目调度，也仅考虑了各项目独立的情况。RCPTTSP-PS不仅将项目拆分与作业调度同时纳入决策模型，还考虑了转换前后的2个装配项目对于资源、工期和节拍时间的差异，以及2个项目相互影响的复杂情况。现有算法难以求解RCPTTSP-PS，因此对RCPTTSP-PS进行建模与算法研究，有着重要的理论意义。

1 问题描述及数学模型

1.1 问题描述

RCPTTSP-PS以飞机总装脉动生产线的节拍转换过程为实际应用背景。在脉动生产线上，根据实际生产线长度L、飞机长度LA、安全距离SD，装配线被分为N个装配单元，总装项目也被拆分为N个作业子集并分配给各个装配单元。由于新项目的进入和原项目的完工，整个转换过程在时间上被分为多个阶段。如图1所示，飞机沿装配线方向逐步完成装配，转换期前后，装配线上都仅有一种类型飞机，装配线稳定无变动，而转换期内，装配线由2种飞机（G0，G1）的作业子集构成，每过一个周期时间，飞机都会沿装配线方向移动一个装配单元，各装配单元对应的作业子集都会改变。在此过程中每个周期内调度计划均不同，周期内的资源需求和周期时间也均会发生变化。以转换期时长最小化为优化目标，建立数学模型并求解。

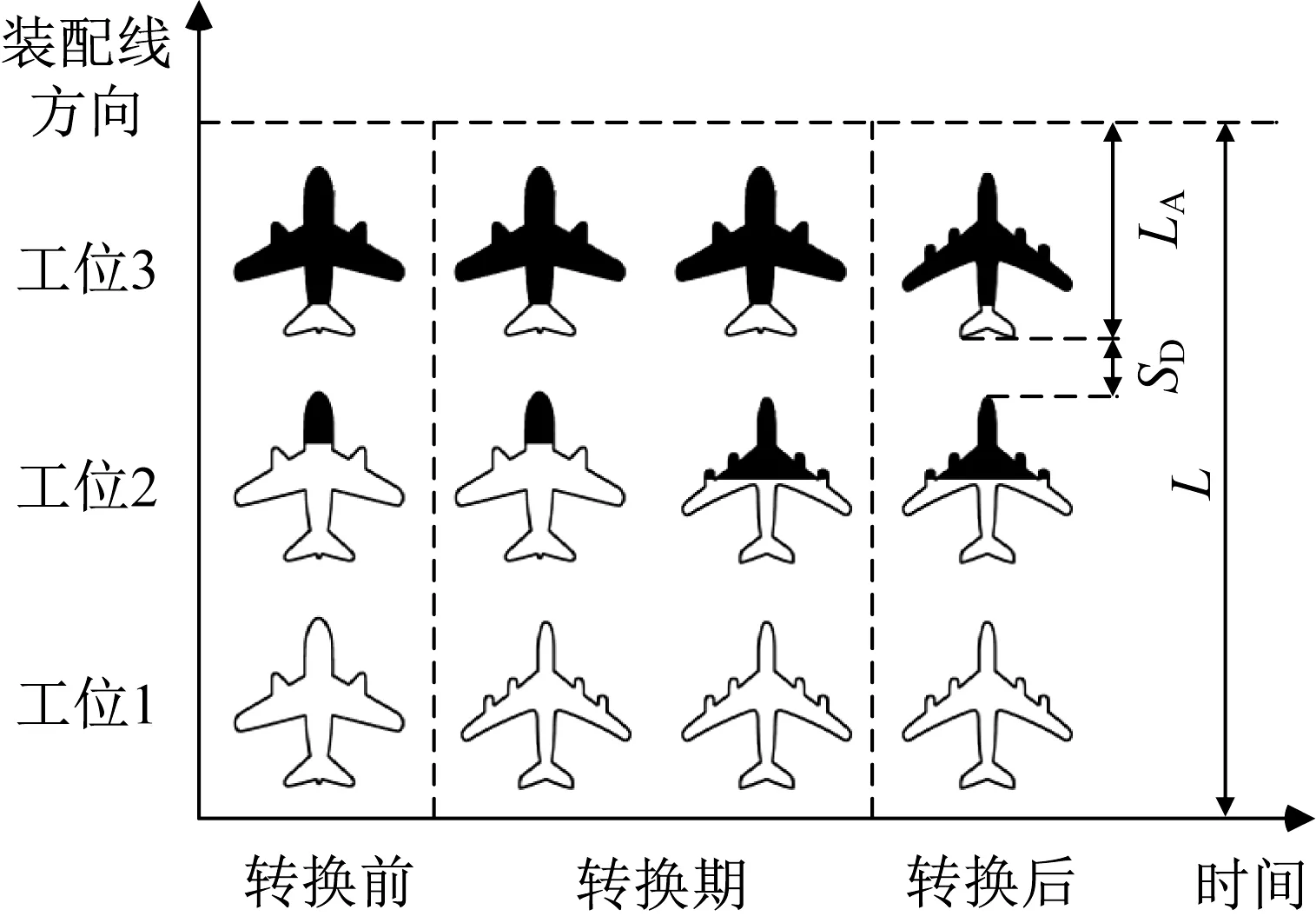
图1 飞机移动装配线转换过程Fig.1 Aircraft moving assembly line transition process

为了描述拆分之后的时序约束关系，给出如下定义：

定义1真实时序约束。对于在初始项目网络中存在时序约束的2个作业，若项目拆分后2个作业仍处于同一个作业子集内，则2个作业间的时序约束仍然存在，称该约束为真实时序约束。

定义2虚拟时序约束。对于在初始项目网络中存在时序约束的2个作业，若项目拆分后2个作业不处于同一个作业子集内，则2个作业间不存在时序约束，仅在拆分时需要考虑，称该约束为虚拟时序约束。

定义3同源作业子集。如果一系列作业子集拆分自同一架飞机的总装项目，就称这一系列作业子集为同源作业子集，也被称为同源子项目。

图2为转换过程中项目的拆分方案以及时序约束关系。其中，数字代表装配作业，实线有向弧代表真实时序约束，虚线有向弧代表虚拟时序约束。在考虑了拆分的飞机装配过程中，不同周期内的同源作业子集间会有虚拟时序约束，同时同源作业子集间可以进行作业的移动以优化拆分方案。在调度时，只有真实时序约束会被考虑；在作业移动时，真实时序约束和虚拟时序约束都需要纳入考虑。

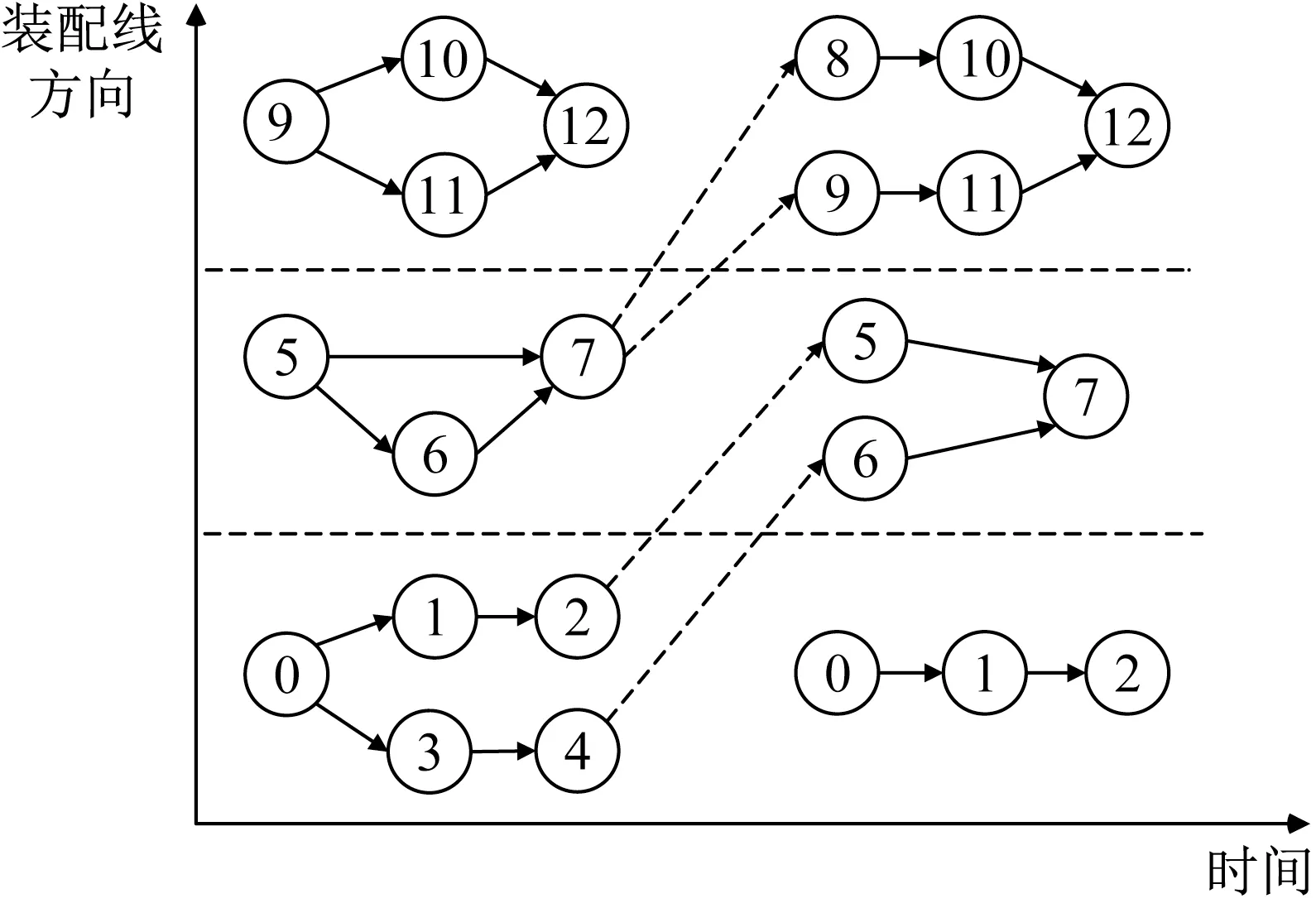
图2 转换过程拆分方式Fig.2 Splitting method in transition process

此外，为了着重研究项目转换，给出如下假设：作业执行不可中断，当前周期内所有作业完工后才能进入下一周期，作业只有一种执行模式。

1.2 数学模型

根据以上问题描述，给出具体参数定义。模型中部分参数如表1所示。

表1 部分参数符号及说明Tab.1 Some parameter symbols and their descriptions

（1）决策变量

xtjmn为0、1变量，若装配周期m时装配单元n上作业j的开始时间为t，则xtjmn=1，否则xtjmn=0。

yjmn为0、1变量，若作业j属于作业子集Smn，则yjmn=1，否则yjmn=0。

zpjmn为0、1变量，表示作业的真实时序约束，若作业p是作业j的紧前作业，并且拆分后在同一个作业子集Smn中，则zpjmn=1，否则zpjmn=0。

（2）目标函数

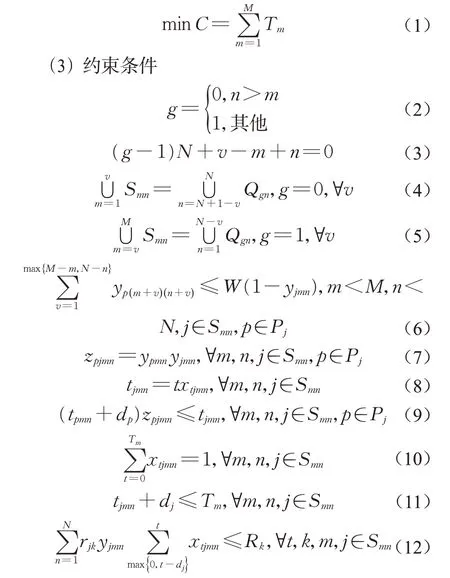
式（1）是目标函数，即要求转换过程的总时间最小。式（2）和式（3）表达了4个参数g、v、m、n之间的关系，如图3所示。图3中，一个圆角矩形表示一个作业子集，该作业子集所属的飞机类型g与项目序号v用于确定作业子集在生产计划中的位置，具有相同g、v的作业子集属于同一飞机，互为同源作业子集，图3中双向箭头表示同源关系。作业子集对应装配周期m与装配单元n，用以确定作业子集的位置，m相同的作业在同一周期内装配，共享线边资源。

图3 作业子集序号关系Fig.3 Relationship between sub-projects’sequence numbers

式（4）和式（5）保证每一组同源作业子集完成了所有需要完成的作业；式（6）表示所有作业的紧前作业不能分配到该作业所在作业子集的后序同源作业子集中；式（7）表示真实时序约束zpjmn与项目拆分决策变量yjmn的关系，当作业与其紧前作业被同时分配到同一个作业子集时，真实时序约束生效；式（8）表示作业开始时间与决策变量xtjmn的关系；式（9）限制作业子集内的优先次序关系，作业必须在其紧前作业完工后才能开始；式（10）表示每个作业只开始一次，并且开始后不能中断；式（11）表示每个作业都要在节拍时间内完成；式（12）表示资源约束，即每个时刻所使用的资源不能超过资源上限。

2 算法框架

针对所研究的问题，采用双层迭代算法。上层使用双重禁忌搜索（DTS）算法对作业拆分方案进行搜索，在作业子集之间进行作业的移动以搜索最优的拆分决策；下层使用基于最小最晚结束时间（MIN LFT）的优先级规则并结合串行调度生成机制进行调度，将每个作业子集的完工时间及资源使用比反馈给上层的双重禁忌搜索算法，通过不断的循环迭代使目标函数最小化。

2.1 双层迭代算法整体步骤

步骤1根据非转换期的项目拆分方案，依照进入装配线的顺序进行项目组合，构造原始拆分方案，并利用最小最晚结束时间优先级规则进行串行调度，求解初始转换期总时长C0，令Cbest=C0。

步骤2设置总迭代次数为E，初始迭代次数e=1。

步骤3计算各作业子集的完工时长Cmn，利用概率密度函数ψ(m，n，i)计算作业移动的起终点项目的选取概率，其中i表示同源作业子集之间的距离。

步骤4判断是否有满足特赦条件的起终点的选取概率，如果有，转步骤6。

步骤5采用偏移随机抽样（RBRS）算法和相对禁忌表确定作业移动的起终点项目序号。

步骤6利用作业选取规则选取移动作业。

步骤7查询移动后的项目关键链是否在绝对禁忌表中，若在则重新选取移动作业。如果所有作业移动后的项目关键链均在绝对禁忌表中，就转步骤5重新选择起终点对。

步骤8采用最小最晚结束时间优先级规则对各周期内的拆分方案进行串行调度，计算每个周期的完工时间Tm、各周期内资源利用率fkm以及当前迭代的转换期总时长Ce，若Ce＜Cbest，则Cbest=Ce。

步骤9将起终点对加入相对禁忌表。

步骤10对移动后的拆分方案计算关键路径长度，判断是否要加入绝对禁忌表。

步骤11e=e+1，若e＜E，则转步骤3。

步骤12输出Cbest。

2.2 基于双重禁忌搜索算法的作业移动

提出了一种双重禁忌搜索算法，加入了相对禁忌表和绝对禁忌表来处理不同的禁忌情况。相对禁忌表即为常规禁忌搜索算法中的禁忌表，可持续更替。绝对禁忌表则存储无法达到历史最优的解的特征，在搜索过程中不断增加。相比传统元启发算法，该算法通过绝对禁忌表增加约束，缩减解集的搜索空间，利用相对禁忌表和启发式规则来控制解的搜索方向，两者相结合进行最优解的搜索。

2.2.1 作业起终点项目的选择

首先计算出当前每个作业子集Smn的完工时间Cmn，通过Cmn计算起点与终点的权重比ρmn。ρmn的计算式如下所示：

由于不同的作业子集间可能拥有同一个项目的继承关系，因此仅有同源作业子集间可以进行作业移动。同源作业子集有如下性质：

性质1对于一系列同源作业子集Smn，根据式（1），有m、n之差为常数。定义Smn的同源作业子集为S(m+i)(n+i)，i∈Z，i≠0。

在性质1的基础上引入i作为作业移动起终点作业子集在其整装项目中的序号差，以确保选取的起终点作业子集为同源作业子集。设概率密度函数

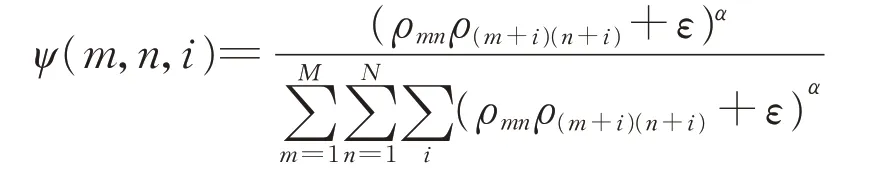
式中：ε＞0为参数，用于保证ρmn=0的项目也有一定概率被选择；α为用于控制过程随机性的参数。ψ(m，n，i)的值决定作业子集Smn被选中起点并移动i个单位的概率。因同源作业子集间存在虚拟时序约束，因此每次移动时仅移动一个单位，i=±1，表示作业移动的方向与距离。

2.2.2 相对禁忌框架设计

（1）相对禁忌表

使用相对禁忌表的目的是跳出局部最优，避免搜索选入循环。本研究中相对禁忌表记录的是记录之前若干次移动所选取的起终点作业子集序号Smn、S(m+i)(n+i)。

（2）相对禁忌长度

禁忌对象为起终点作业子集序号，禁忌对象的总数相对较少。如图4所示，N=3时可选取的起终点对仅有4对，N=4时有12对，N=5时有24对。拆分数量对于可移动的起终点影响很大，因此禁忌长度LTabu的选取也很关键。本研究中取LTabu=

图4 不同拆分数量下转换期Fig.4 Transition process of different splitting numbers

N-2。

（3）特赦规则

对于完工时间最长的起点Smn，若其可移动的终点S(m+i)(n+i)的完工时间为（m+i)周期内的最小值，且m和(m+i)周期内的资源利用率分别为全周期内最高和最低时，对Smn、S(m+i)(n+i)特赦。选取Smn、S(m+i)(n+i)为调整的起终点。若存在多个可特赦起终点项目对，则随机选取一对起终点。

2.2.3 作业选取

定义4作业移动。对一个作业j∈Smn，将其从Smn移动至S(m+1)(n+1)，称为作业右移；将其从Smn移动至S(m-1)(n-1)，称为作业左移。

定义5松弛约束。作业j与作业q在移动前存在真实时序约束，在移动后真实时序约束转化为虚拟时序约束，称为松弛约束。

定义6绑定约束。作业j与作业q在移动前存在虚拟时序约束，在移动后虚拟时序约束转化为真实时序约束，称为绑定约束。

作业移动过程如图5所示。当目标作业移动时，目标作业与起点作业子集的其他作业松弛约束，真实时序约束变少，因此作业子集的关键链长度变短，对应作业子集工期变短；目标作业与终点作业子集的其他作业绑定约束，真实时序约束增加，因此作业子集的关键链长度变长，对应作业子集工期变长。

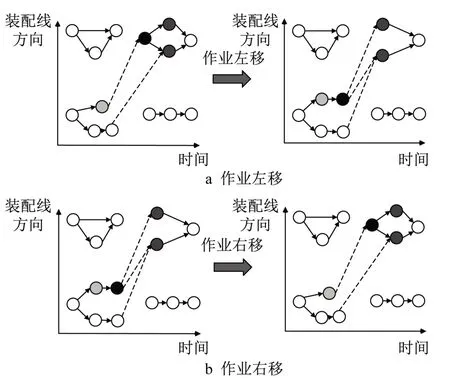
图5 作业左（右）移分析Fig.5 Analysis of job moving left(right)

作业移动的具体作业选取与时序约束的改变如下：

（1）当作业左移时，只有无真实紧前时序约束的作业j可以被选中，参数γ1j表示目标作业在移动前的真实紧后作业约束数量，参数γ2j表示目标作业在移动后的真实紧前作业约束数量，Δγj=γ1j-γ2j。

（2）当作业右移时，只有无真实紧后时序约束的作业j可以被选中，参数γ1j表示目标作业在移动前的真实紧前作业约束数量，参数γ2j表示目标作业在移动后的真实紧后作业约束数量，Δγj=γ1j-γ2j。

此外，作业是在项目转换期内不同周期间进行作业移动，起点周期内调度作业减少，资源约束松弛，对应周期的整体工期变小；终点周期内的调度作业增多，资源约束收紧，对应周期的整体工期变大。因此，在选择了作业移动的起终点后，将结合真实时序约束与资源约束2个方面来选取作业进行移动。作业选取的权重参数δj=Δγj/J+uj，其中Δγj/J表示解绑的时序约束数量与总作业数的比值，uj=rj1(1-f1m)+…+rjK(1-fKm)为资源评估函数，其具体含义为作业j在周期m内使用的资源与周期m所使用的全部资源的比值周期m资源k的使用率。δj将作业j移动的真实时序约束变化与资源变化同时纳入考虑，默认选取δj最大的作业进行移动。当存在δj相同的作业时，添加补充规则：作业左移时，选取序号最小的作业；作业右移时，选取序号最大的作业。

2.2.4 绝对禁忌规则

（1）绝对禁忌表

绝对禁忌表的目的是筛选所有不可能成为最优解的可行解的特征，以此来减少解的搜索空间。本研究中，绝对禁忌表的禁忌对象为拆分方案的关键链。每次移动后，需计算移动后拆分方案的关键链，若关键链长度大于历史最优解Cbest时，将该关键链包含进绝对禁忌表中。绝对禁忌表有如下性质：

性质2包含绝对禁忌表中关键链的拆分方案均不是最优解。

证明绝对禁忌表中的关键链所对应的解不是唯一的，所有包括这条关键链的项目拆分方案，其完工时间均大于关键链长度。又因为关键链的时长大于历史最优解Cbest，因此拆分方案完工时间C＞Cbest无法成为历史最优解。

因为绝对禁忌表的性质2，绝对禁忌表不受限于禁忌长度，所以绝对禁忌表不会解除禁忌。

（2）绝对禁忌规则

当作业移动后，若移动后产生的新拆分方案中包含绝对禁忌表中的关键链，则新方案不被接受，返回作业选取步骤顺次按权重δj选取下一个可移动作业。如果所有移动方案均在绝对禁忌表中，就跳过本次移动，选取新的项目调整起终点。

3 数值实验

3.1 实例验证

为了验证算法和模型的可行性，选用PSPLIB提供的算例作为某工厂所装配的飞机项目G0、G1，使用Python3.7.0编程实现算法。数据测试平台选用i5-4210U处理器，2.39 GHz主频，8 G内存。项目G0、G1各包括30个作业及2个虚拟作业，4种完成项目所需的可更新资源，具体数据如表2所示。某工厂需要将飞机移动生产线从G0转换至G1，计算转换的总工期并使得总时间最小化。采用所提出的模型及算法，对于G0、G1确定的拆分数量N=3，算法参数设定α=1，ε=1，LTabu=1，E=100。

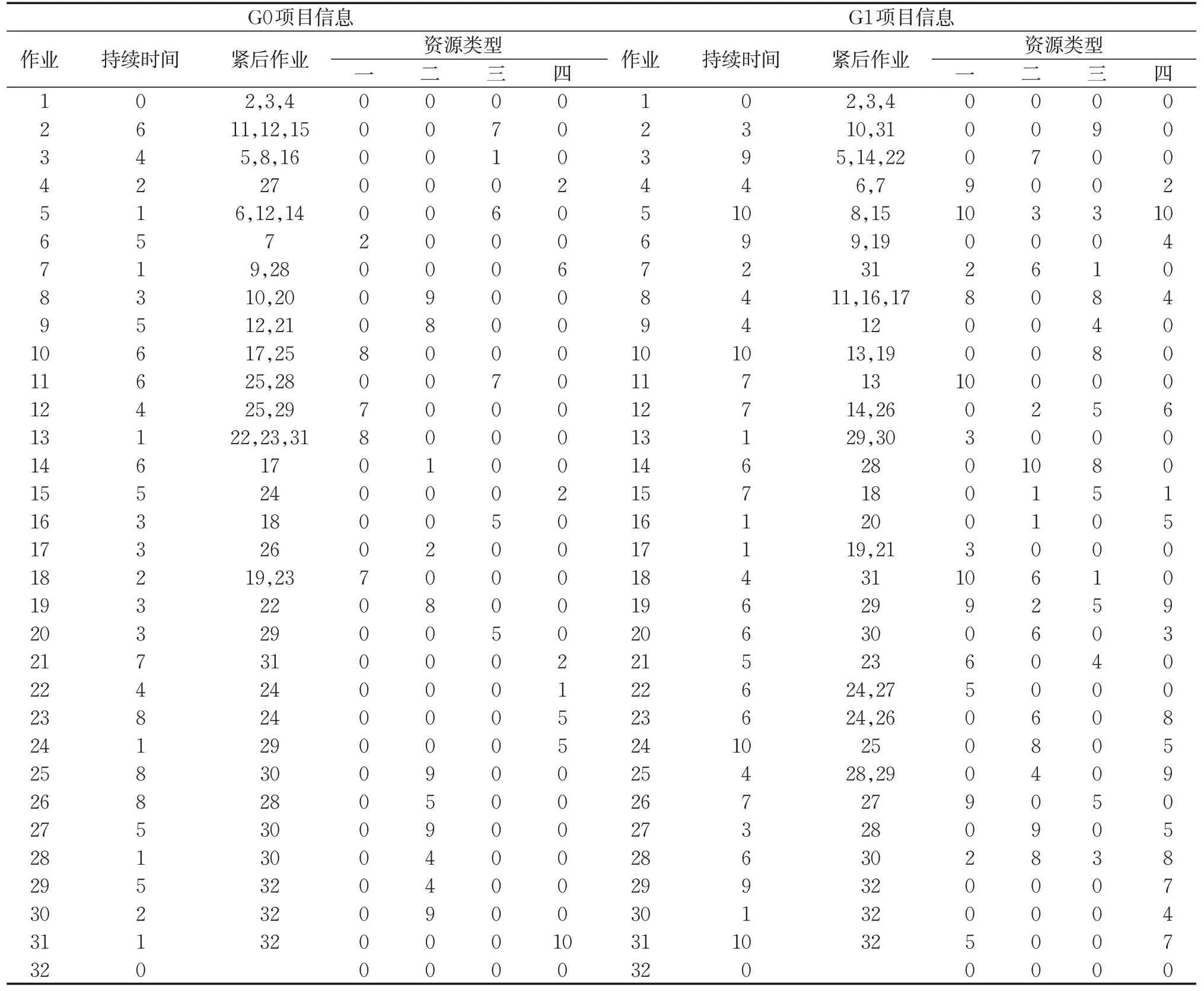
表2 项目数据Tab.2 Project data

为了进一步验证本研究模型和算法的可行性，以同样的转换过程，与不进行重拆分的调度方案初始解进行对比。给定各类资源上限均为15，初始解的具体拆分方案如表3所示，本研究算法优化的重拆分方案如表4所示，2种拆分方案的对比结果如表5所示。可以看出，采用本研究方案的项目时长显著小于不经过调整的方案。在实际生产中，使用本研究方案在转换过程中进行变节拍生产，可以提高生产线的生产效率。

表3 初始拆分方案Tab.3 Initial splitting plan

表4 转换期拆分方案Tab.4 Transition splitting plan

表5 转换期节拍时间对比Tab.5 Cycle time comparison during transition period

3.2 算法分析

选取参数ε=1以确保ψ(m，n，i)不为零，初始拆分方案依文献［10］进行计算，因为初始拆分方案已经是项目的最优解，所以取迭代次数E=100，N=5，LTabu=3。对控制移动方向的随机参数α进行敏感性分析，选取标准算例库中的3种作业规模J30、J60、J90的各40个项目进实验。3种算例下，比较差值百分比的均值图6是参数α的敏感性分析。可以看出，当α=1时值最小，所以实验时取α=1。

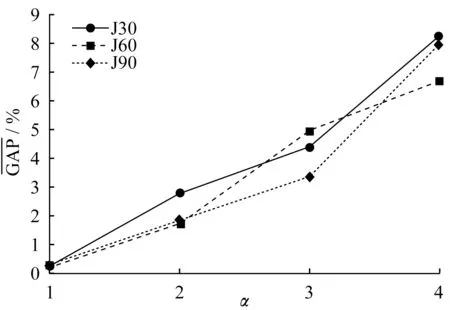
图6 α对调度结果的影响Fig.6 Effect ofαon scheduling results

3.3 算法比较

由图4分析可知，计算规模随着拆分数量的增加呈幂函数增长，常规的精确算法难以求解，故选取已有的项目拆分问题启发式算法［10］结合项目节拍转换过程，将遗传算法与本研究算法进行对比。引用标准算例库PSPLIB中的3种作业规模J30、J60、J90，在N=3，4，5的情况下，分别随机选取5对项目进行项目转换，参数设定α=1，E=100，LTabu=N-2。

表6～8列出了3种规模下3种拆分数目结果的对比。GAPGA与GAPBASE的计算式分别如下所示：

式中：C为转换期总时长；GA表示遗传算法，BASE表示初始拆分方案，DTS表示本研究方案。表6～8中，t为求解时间。对于GA，取迭代次数100，初始种群数10，交叉概率0.8，变异概率0.2，对作业所属项目进行编码。

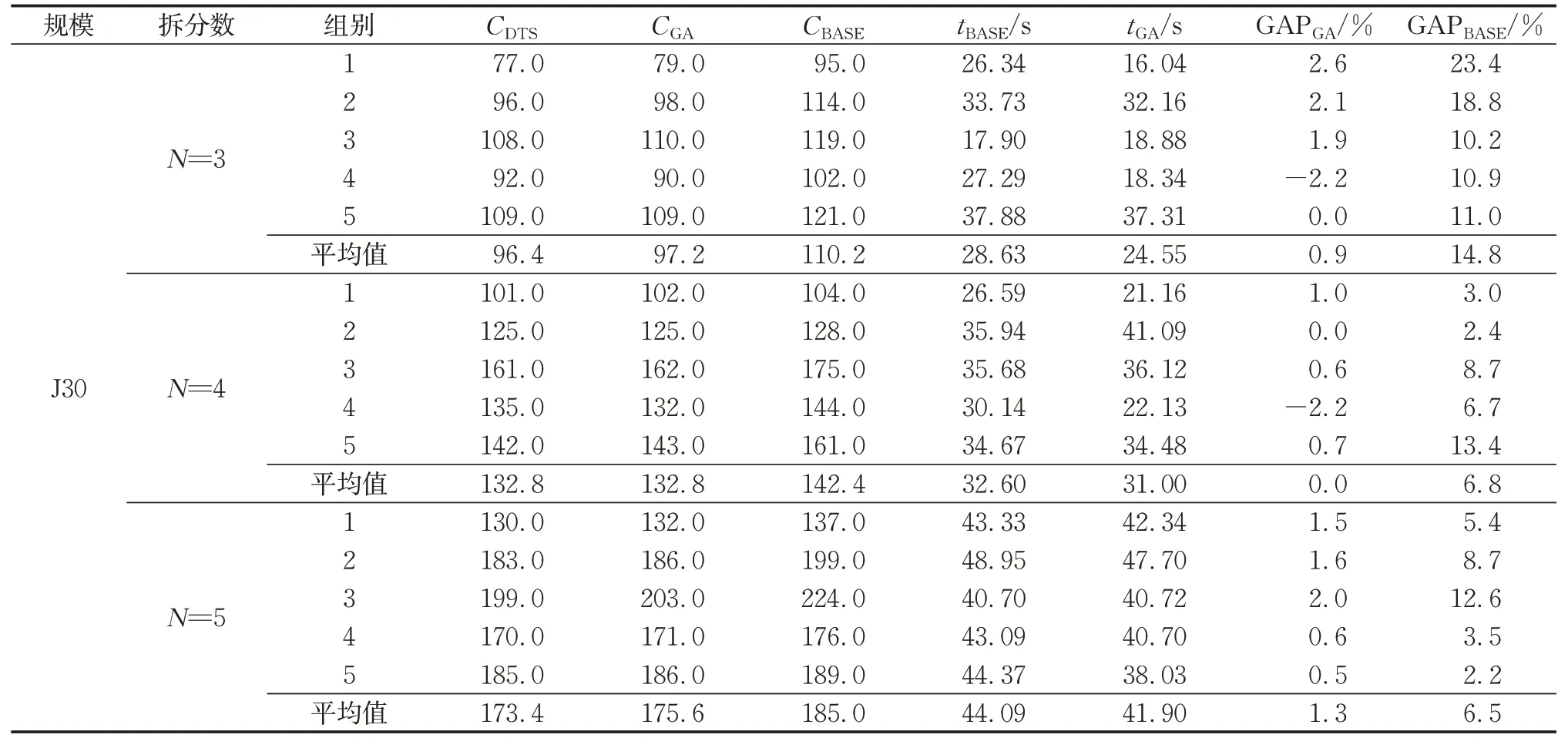
表6 J30规模数值结果Tab.6 Numerical results of J30

表7 J60规模数值结果Tab.7 Numerical results of J60

通过表6～8可以得出，在求解小中大3种规模的算例时，本研究算法平均质量均优于对比算法GA，但对于部分项目，如J30、N=4、第4组项目时，本研究算法的求解效果不如对比算法。与对比算法差别较小的原因可能是两者均在初始拆分方案的基础上进行进一步搜索，因此搜索的方向相似。从整体上看，本研究算法与对比算法之间的GAP稳定在3%以内，并且平均求解质量优于GA约1%，这是由于双重禁忌搜索限制了搜索空间，提高了搜索质量。从与初始拆分方案的GAP值上来看，本研究算法对于初始拆分方案的优化程度平均在10%左右，但是不同的项目间波动较大，最高值可达23.4%，最低值仅有1.1%，这是由于本研究算法是在已有的项目拆分方案上进行进一步优化，可优化区间主要来自于转换的两项目间的差异。对于相似的2个项目，初始拆分方案是类似的，在转换期间对资源的需求和节拍时间的要求都相似，因此优化的空间有限。对于差异性较大的项目，本研究算法的优化空间更大。在不同规模的算例下，拆分数并未对优化结果产生显著的影响，但是从约束角度分析，随着拆分数增大，被松弛的真实时序约束增多，作业调度的自由度就更高。当拆分数与作业数相等时，该问题将退化为一个没有时序约束的项目调度问题。因此，随着拆分数的增大，每个周期的节拍时间有减小的趋势。在算法的运算速度方面，随着项目规模和拆分数的增加，本研究算法和GA的求解时间都在增大。在项目规模较小时，GA的求解时间略小于本研究算法，但是当项目的规模数达到J60和J90时，本研究算法的求解时间显著小于对比算法，这说明本研究算法对大规模项目的适应性较好，而对于小规模算法求解速度较差。

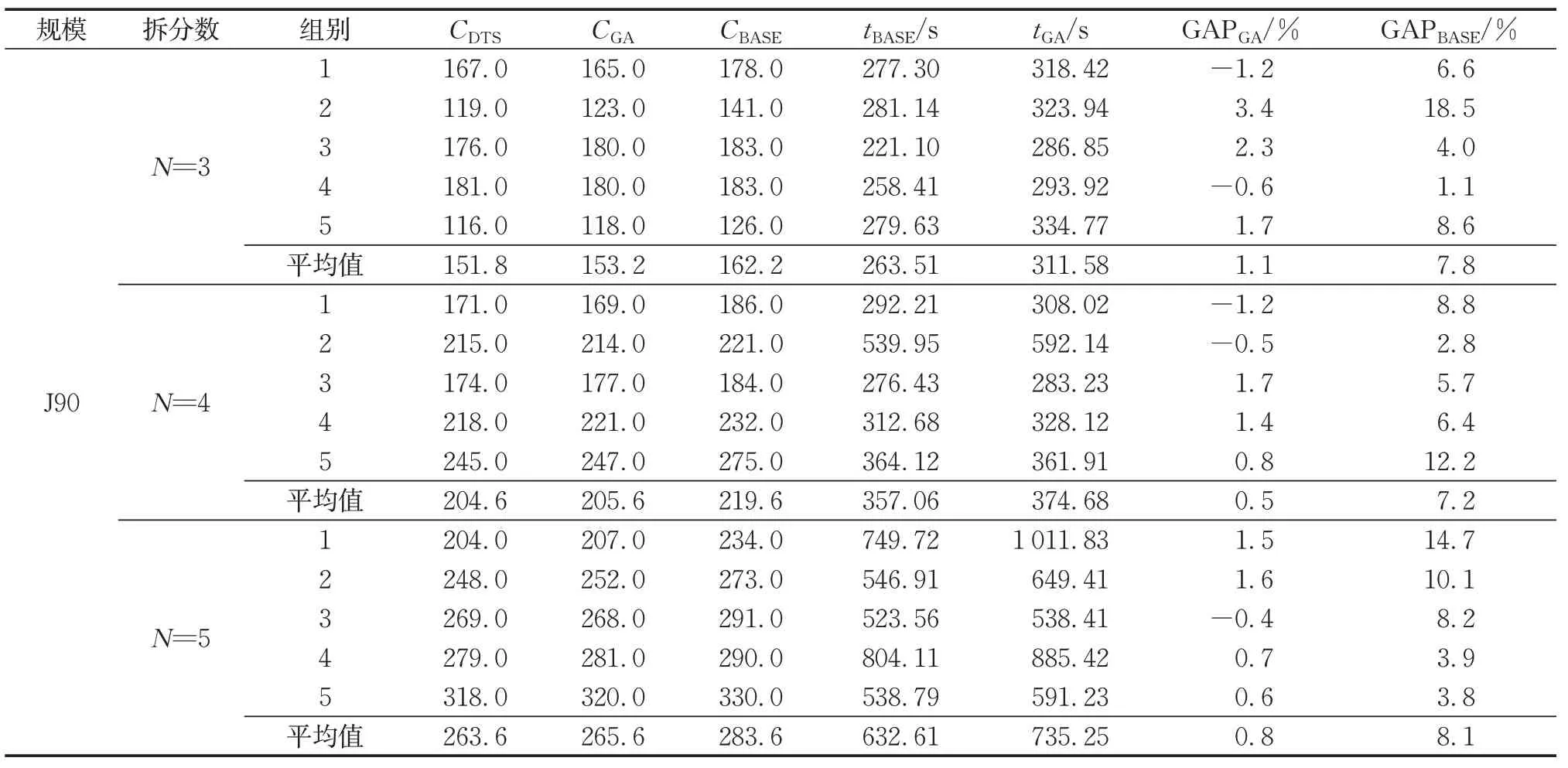
表8 J90规模数值结果Tab.8 Numerical results of J90

4 结语

以RCPTTSP-PS为研究对象，建立了离散时间下的数学模型，提出了双重禁忌搜索算法，并结合双层迭代算法对问题进行求解。在项目转换阶段，考虑了项目移动对起终点项目的共同影响，提出了起终点选取函数以及作业选取权重函数。同时，为了限制搜索空间，提出了相对禁忌规则和绝对禁忌规则，有助于避免算法陷入局部最优，并利用绝对禁忌规则限制搜索空间，提高了搜索速度。在数值实验中，本研究算法的求解质量略优于对比算法，与对比算法的GAP值在1%左右。在求解速度方面，本研究算法在大规模项目的求解速度明显优于对比算法。因此，本研究算法对于飞机脉动生产线这类大规模项目调度问题具有良好的效果。同时，相较于初始拆分方案，本研究算法对于转换期时长的优化程度在1.1%～23.4%之间，与初始拆分方案的GAP值方差较大，这是由不同项目网络之间的差异引起的。在未来的研究中，可以对RCPTTSP-PS中不同项目的关联性进行进一步研究，有助于提高生产线节拍转换过程的时间优化，对于生产线上的实际应用也有一定帮助。