具有径向基网络加速度反馈的磁浮列车悬浮系统滑模控制
陈 琛,徐俊起,林国斌,荣立军,孙友刚
(1.同济大学道路与交通工程教育部重点实验室,上海201804;2.同济大学国家磁浮交通工程技术研究中心,上海201804;3.同济大学交通运输工程学院,上海201804)
磁浮列车的无接触运行能够有效降低维护成本,具有低噪音下高速运行的可行性。悬浮系统是磁浮列车的重要组成部分,其在很小的可调间隔内的稳定性控制是磁浮领域最经典、最具挑战性的内容之一[1-4]。
由于线性控制的局限性,因此磁耦合引起的车-轨共振对磁浮列车的运行稳定性有很大影响。另外,如果在复杂扰动(负载不规则变化扰动、轨道梁挠度变形以及F型轨接缝造成的不平顺扰动)下悬浮间隙控制响应不及时或无法自适应收敛就会导致列车悬浮失稳。为了有效提高悬浮稳定性,抑制磁耦合振动,有必要结合列车悬浮系统的动态性能,研究一种更可靠的含有振动抑制功能的悬浮控制算法[5-7]。Wai等[8-9]针对具有非负输入的线性磁浮列车磁轨系统设计了一个具有强鲁棒性的模糊神经网络控制(RFNNC)方案,并在不确定因素存在的情况下保证被控系统的稳定性。刘丽丽等[10]针对悬浮系统非线性和迟滞性的特点,提出一种模糊比例-积分-微分(PID)控制算法来降低数学模型的精确性,并且通过模糊推理实现参数调整,从而提高系统的自适应能力。王军晓等[11]针对复杂扰动下的磁浮球系统提出了一种基于等价输入干扰滑模观测器的模型预测控制(MPC+EIDSMO)方法,实现对期望悬浮间隙跟踪的快速性和准确性。Chen等[12]基于柔性轨道简支梁和单电磁铁最小悬浮单元设计了滑模自适应状态反馈控制器,并通过仿真和试验与PID控制器和滑模控制器进行对比来说明算法的优越性。Zhang等[13]针对不同时滞环境下的磁浮系统进行了研究,采用多尺度法计算了Hopf分岔的正规型,并通过数值仿真来验证理论分析的正确性。Su等[14]基于模糊理论对有界且小可调区间的悬浮间隙进行了自适应控制,验证了所提出算法在有界扰动下的抗干扰能力。王辉等[15]对柔性轨道下的悬浮状态变量进行研究,并且采用状态预测的方式解决控制性能下降的问题,但是该方法的参数学习能力较弱,无法基于扰动的变化进行自适应调整。
现有的悬浮控制算法在设计过程中没有考虑不规则激励等时变动态扰动,缺乏根据列车振动情况进行的加速度自适应补偿,这就产生了振动激励叠加的情况下悬浮稳定性降低的问题。针对悬浮运行过程中时变激励下的振动抑制问题,提出了一种加速度补偿算法。首先,基于指数趋近律为最小悬浮单元设计了滑模控制(SMBC)算法,并根据稳定性分析确定了具体参数;然后,基于径向基函数(RBF)神经网络的权值自学习功能设计加速度补偿模块,对当前振动采样值进行判断,并进行控制补偿,构造MBC-AFC(acceleration feedback compensation)算法。最后,在单点悬浮试验台上对所提出控制算法进行了验证。
1 悬浮系统建模
磁浮列车通常有多个悬浮点来提供悬浮力。由于悬浮底盘的结构解耦,单点悬浮系统可以作为磁浮列车整体悬浮系统的基本单元[4],因此对单点悬浮系统的讨论更具有普遍性。简化后的最小单元悬浮控制模型如图1所示。其中,zref为期望悬浮间隙,zE为电磁铁垂向振动位移(在不考虑轨道变形时可视为悬浮间隙),Δz1=zE-zref为悬浮间隙误差,FL为悬浮力,mE为电磁铁质量,mD为可变负载质量,L为轨道梁跨度,R为电磁铁绕组电阻,C为电磁铁绕组电感,ic为控制电流[16]。
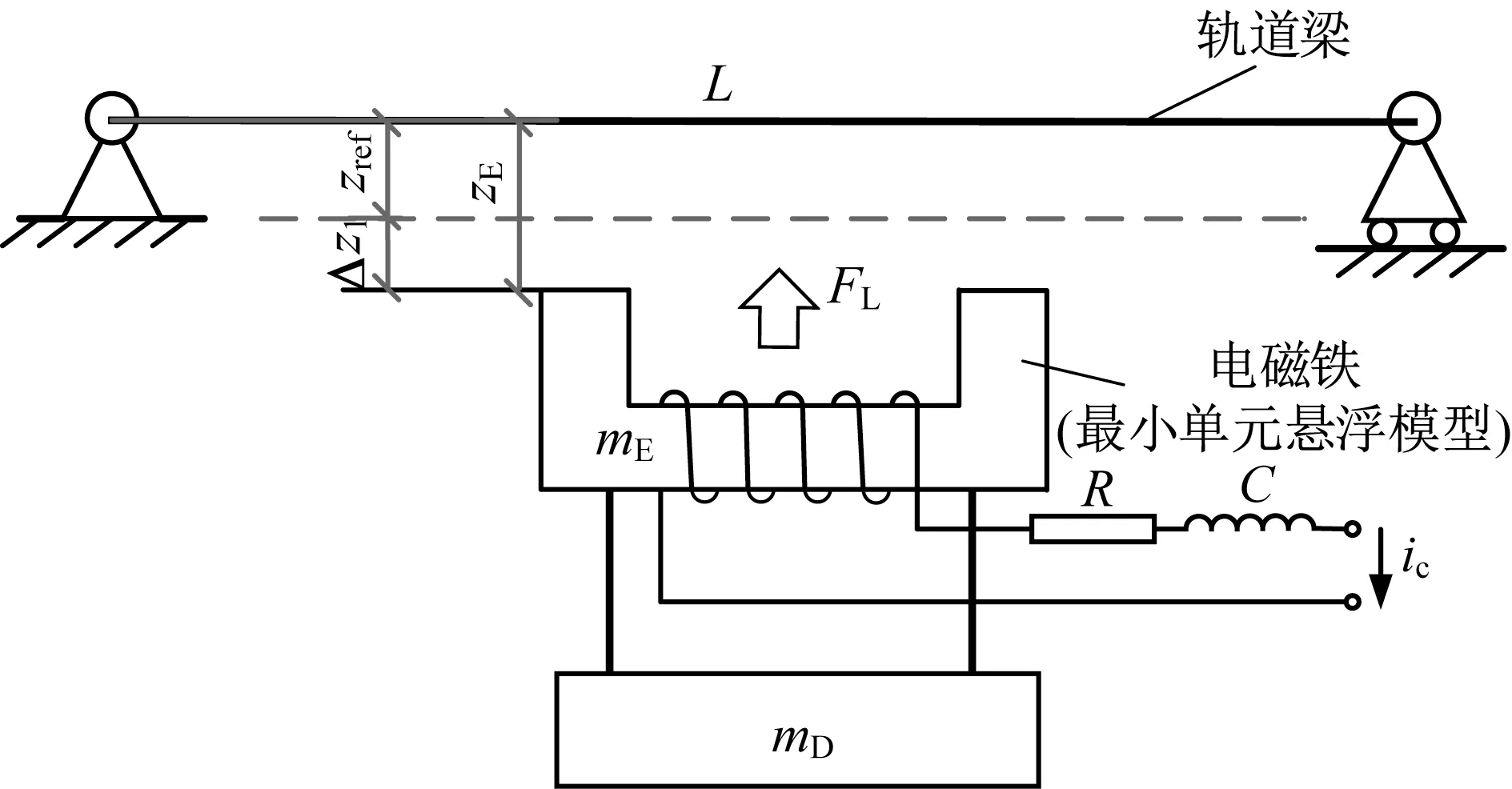
图1 悬浮控制模型Fig.1 Levitation control model
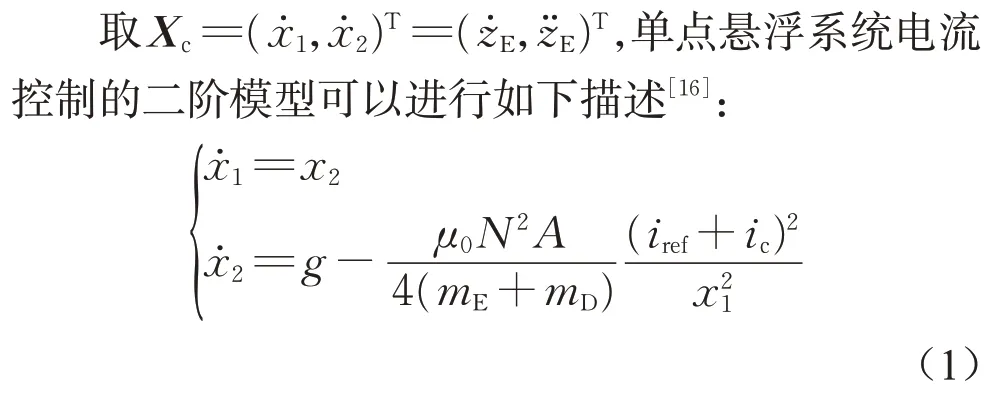
式中:x1为悬浮间隙对应的状态变量;x2为悬浮间隙变化速度对应的状态变量;μ0为真空磁导率;g为重力加速度;N为电磁铁线圈匝数;A为电磁铁磁极面积;iref为平衡点位置期望电流。根据式(1)可以看出,系统控制电流ic和输出悬浮间隙x1具有二阶耦合关系,因此系统具有较强的非线性。车-桥耦合系统参数如表1所示。
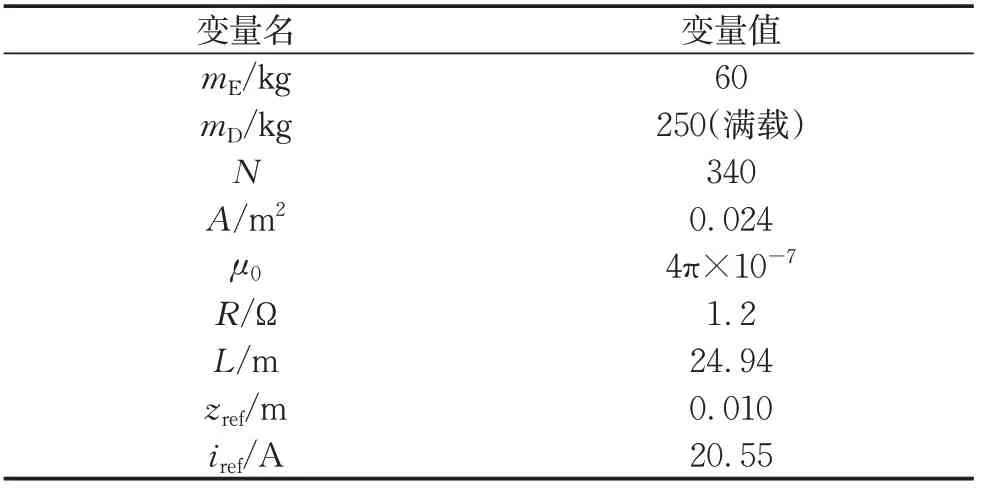
表1 悬浮系统模型参数Tab.1 Parameters of suspension system model

式中:Δz1、Δz˙1分别为悬浮间隙误差与误差变化速度。
2 基于指数趋近律实时反馈的非线性控制律
2.1 PID控制局限性说明
PID控制算法具有性能可靠、原理简单、稳定性好等优点,在悬浮模型等非线性系统中得到了广泛的应用。根据文献[15-16]对悬架控制算法的研究,采用Nyquist准则和根轨迹法确定PID控制算法的参数,其中Kp=14 000,Ki=500,Kd=800。悬浮性能如图2所示。
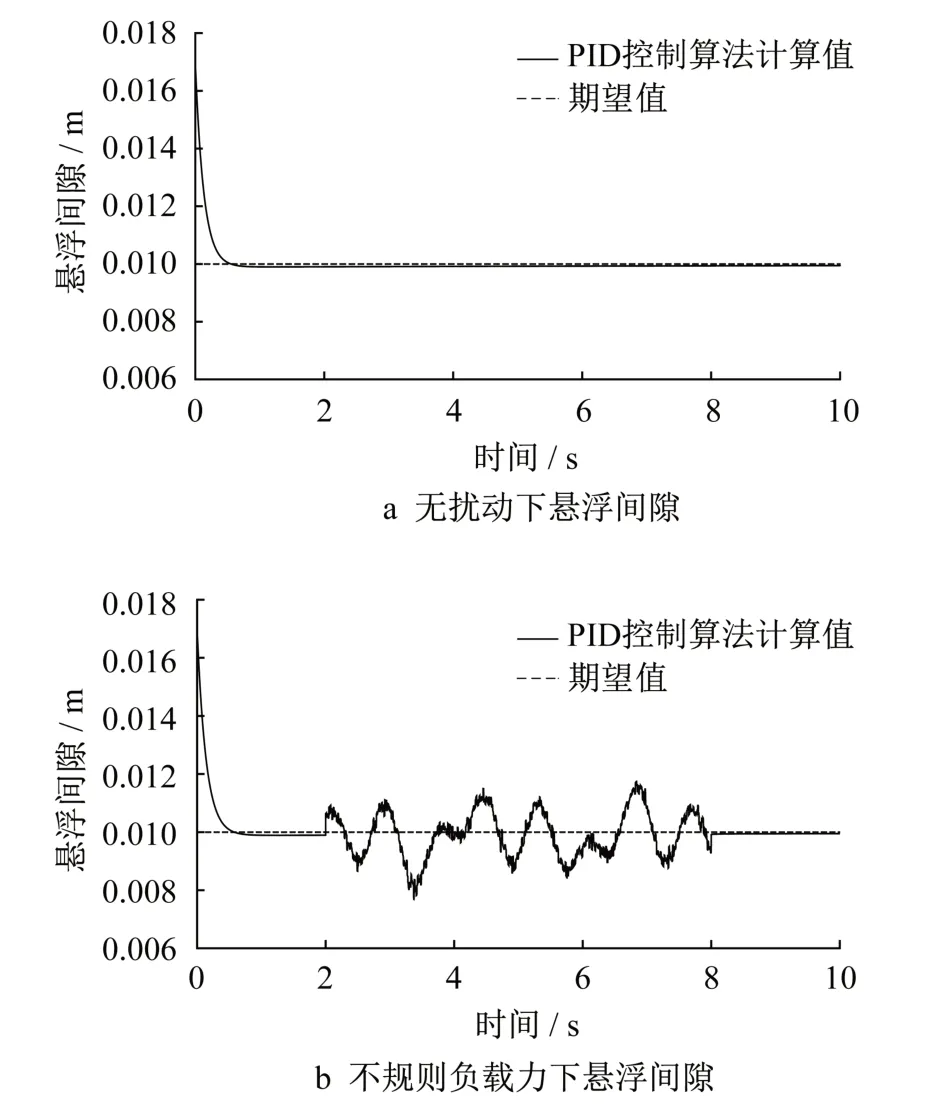
图2 基于PID控制的仿真结果Fig.2 Simulation results based on PID control
列车运行不可避免地受到外界因素的干扰,如车厢内乘客移动引起的荷载变化和轨道梁间连接处的不平顺等。由图2b可以看出,在不规则负载力的作用下,悬浮间隙发生较大波动,因此研究扰动下的动态悬浮过程对提高系统的稳定性和抗干扰能力具有重要意义。
2.2 基于指数趋近律的滑模控制器
为了得到基于指数逼近律的滑模控制律,定义Lyapunov函数V=(1/2)s2,其中s为跟踪误差函数。指数逼近律定义如下所示:

为了保证快速到达滑动面,同时消除抖振现象,在式(3)中可适当增大k,减小ε[12]。
结合如图1所示悬浮模型,令e=Δz1,跟踪误差函数s可以被定义为

式中:c为收敛速率的影响因子。式(7)的导数与式(3)等价,代入式(1)可以得到
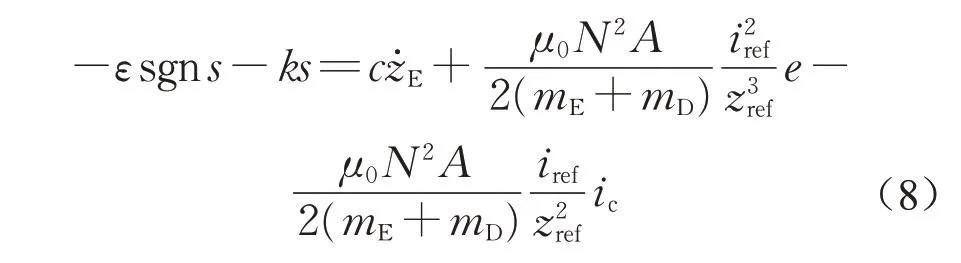
加入平衡点电流iref,并通过进一步求解控制量得到基于指数逼近律的滑模控制律的控制电流,如下所示:
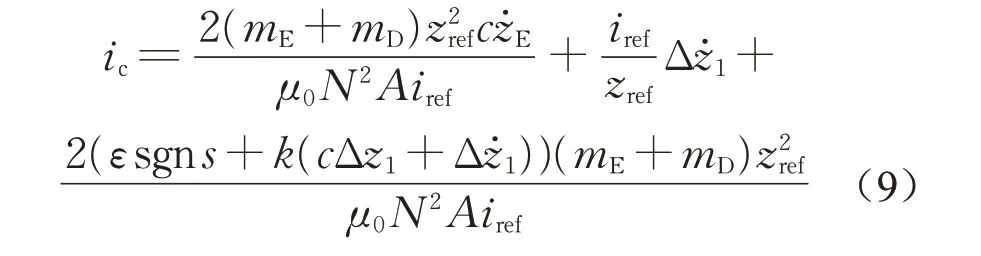
2.3 稳定性分析
对于悬浮系统,当控制量(控制电流)或扰动(不规则性/负载)发生变化并超过某一临界值时,系统的稳定性会发生突变。然而,式(9)中给出的控制律没有考虑参数摄动所引起的不稳定现象。为了抑制不平顺或荷载引起的竖向振动,对式(9)中给出的控制律进行稳定性分析,进一步得到了控制参数的可取范围。
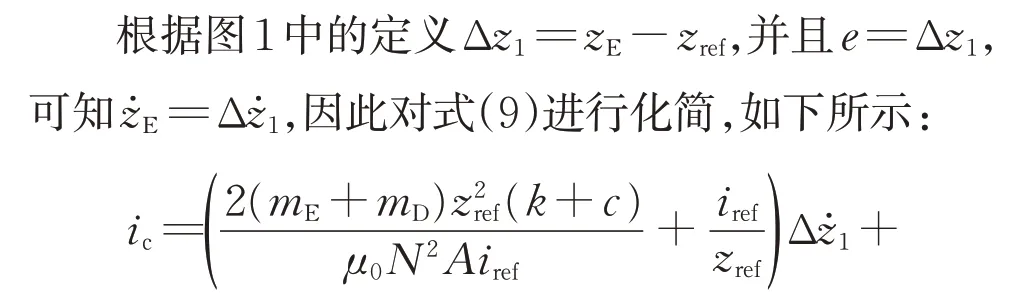
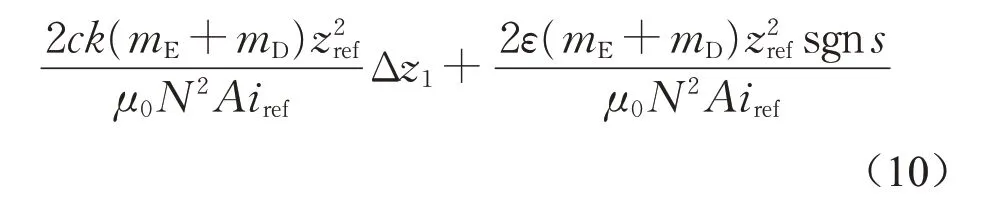
将式(10)代入式(2),可得
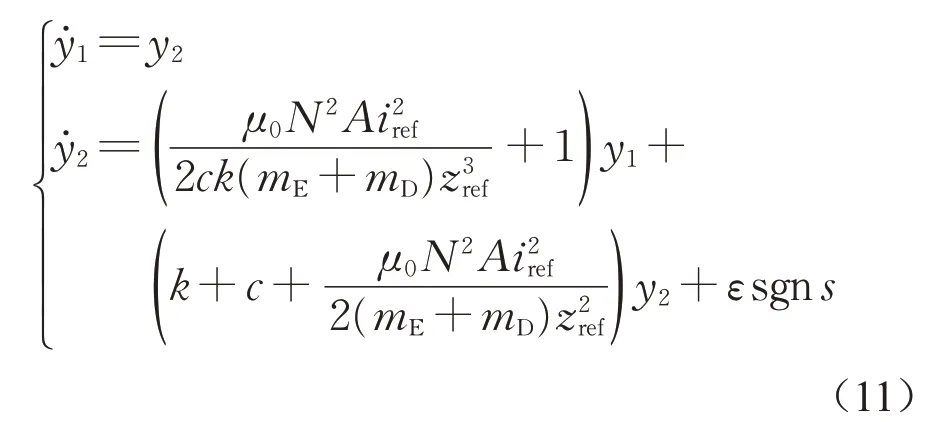
可得对应的特征矩阵,如下所示:

进一步计算可得特征方程,如下所示:
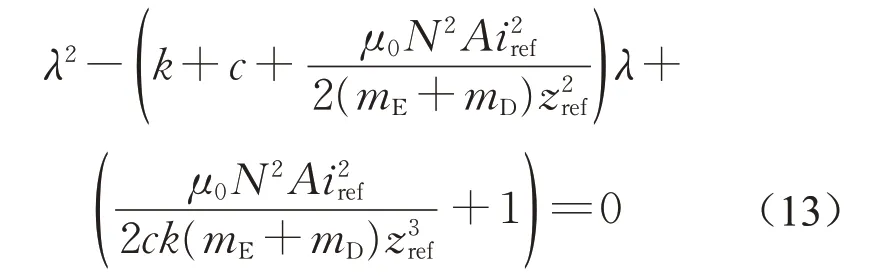
根据Routh-Hurwitz判据可知,为了满足式(12)所示特征方程的根均具有负实部,控制参数需要满足以下边界条件:
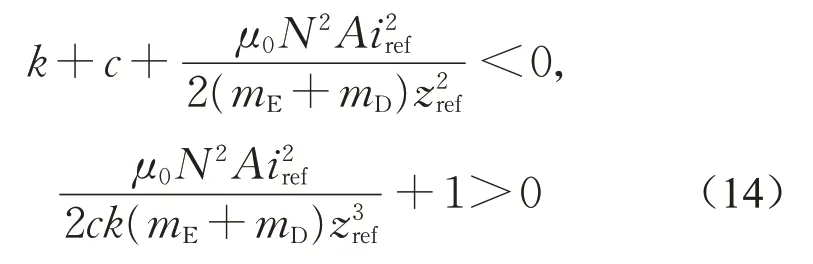
在空载工况下(mD=0)对式(13)进行求解并得到特征根,代入如表1所示参数,得到
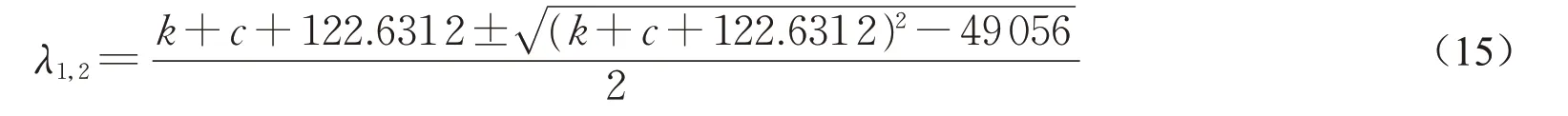
式(14)确保特征根具有负实部,通过对k和c的取值确定约束条件,即k+c<-122.631 2。虚部的求解必然满足这一约束条件,因此求解结果如图3所示。
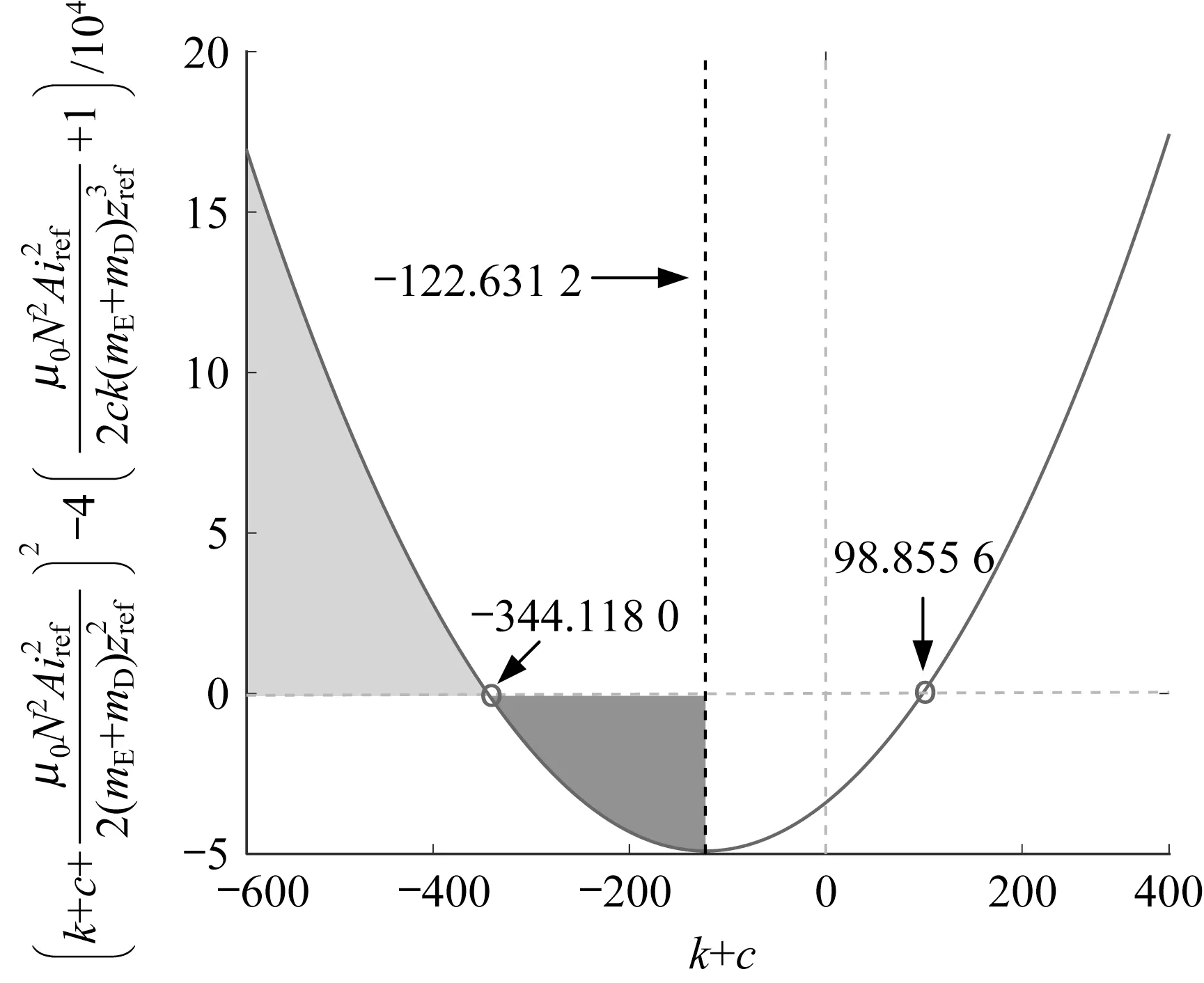
图3 特征根求解结果(空载)Fig.3 Solution results of characteristic root(no loading)
结合式(14),根据Routh-Hurwitz判据的相关结论可以看出,当k+c<-344.118 0时,系统必定具有负实部,并且不存在虚部;当-344.118 0<k+c<-112.631 2时,特征根存在虚部。设特征根λ=α±iβ,此时可将控制系统看作存在阻尼的线弹性问题。α的负数特性表征了系统具有渐进稳定性,β表示系统振动快慢程度。
当k+c=-122.631 2时,系统实部为零,此时平衡点的稳定性将发生变化。然而,根据k+c的取值(特征根具有负实部恒成立),平衡点保持稳定,表明此时所定义的控制参数范围满足稳定性条件。
β在-344.118 0<k+c<-122.631 2区间内的变化范围如图4所示。由图4可知,当k+c=-344.118 0时,虚部为零。此时,能够在最大程度上抑制电磁铁振动。
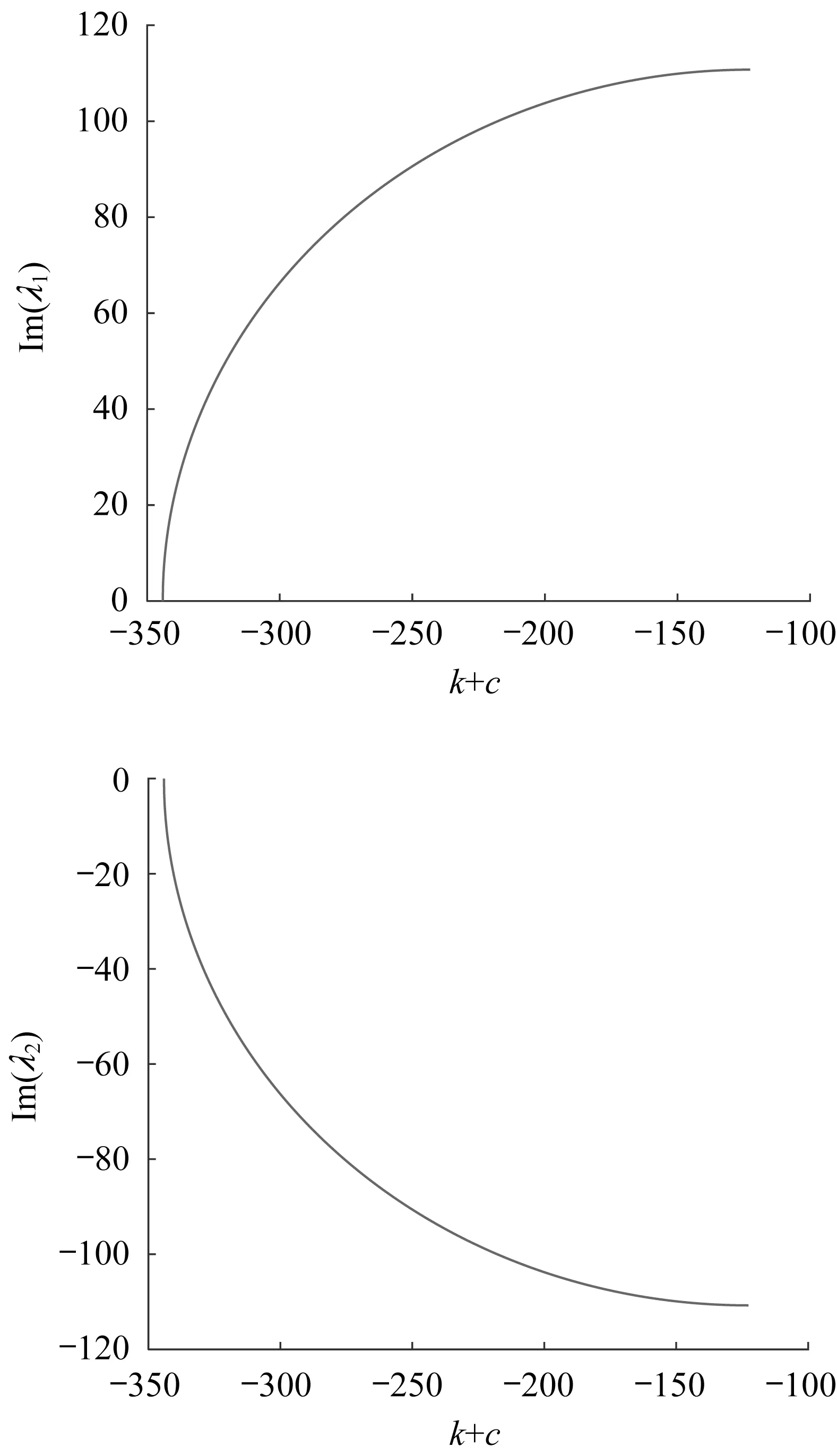
图4 特征根虚部变化规律(空载)Fig.4 Variation of imaginary part of characteristic root(no loading)
在满载工况下(mD=250 kg)进行如式(15)所示的相同计算,得到

为保证特征多项式各项系数大于零,一定满足k+c<-23.735 1。满载工况下特征根求解结果如图5所示。

图5 特征根求解结果(满载)Fig.5 Solution results of characteristic root(full loading)
同理,当k+c<-121.192 6时,系统必定具有负实部,并且不存在虚部。当-121.192 6<k+c<-23.735 1时,特征根存在虚部。虚部β的值越小,说明振动抑制能力越强。β的变化情况如图6所示。
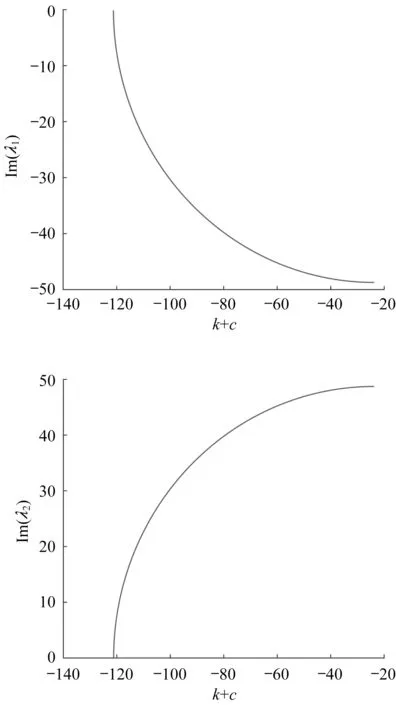
图6 特征根虚部变化规律(满载)Fig.6 Variation of imaginary part of characteristic root(full loading)
2.4 实时加速度补偿优化
根据式(10),控制电流ic所需的主要反馈变量为悬浮间隙和振动加速度。y2可通过对反馈变量进行求导或积分获得。然而,根据以往的工程经验,加速度是描述振动最直接的变量,因此有必要对加速度进行反馈。在采集电磁铁的振动加速度后,还可以根据加速度计算y2。
图7为上海临港中低速磁浮试验线实际试验中,电磁铁(车辆)在60 km·h-1速度下的垂向振动加速度。试验结果表明,列车运行到跨中时,由于轨道梁(桥)的挠曲变形,电磁铁的垂向振动加速度峰值达到1.24 m·s-2,振动最为显著。整个试验过程中,特别当列车在跨中时,加速度需要进一步调整。结合动力学分析,基于加速度反馈的振动(加速度)抑制可以有效提高悬架系统的稳定性。
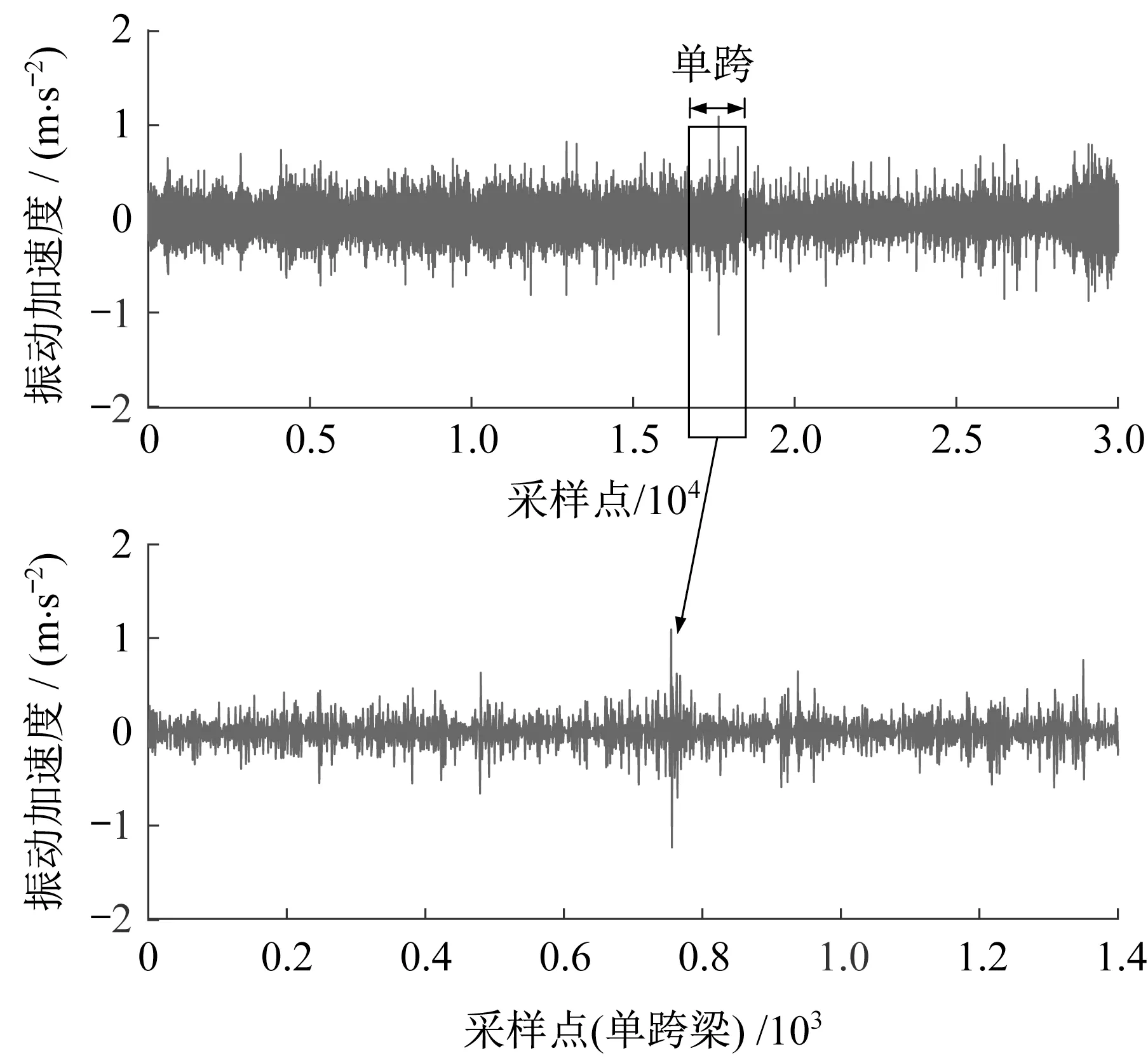
图7 60 km h-1时电磁铁振动Fig.7 Vibration of electromagnet at the speed of 60 km h-1
在此基础上,首先提出了最简单的加速度反馈比例抑振电流is,计算式如下所示。

式中:ksv为加速度反馈增益。
结合式(10)所示滑模控制算法,可以得到所需的具有神经网络加速度反馈的滑模控制算法的控制电流ics,表达式如下所示:
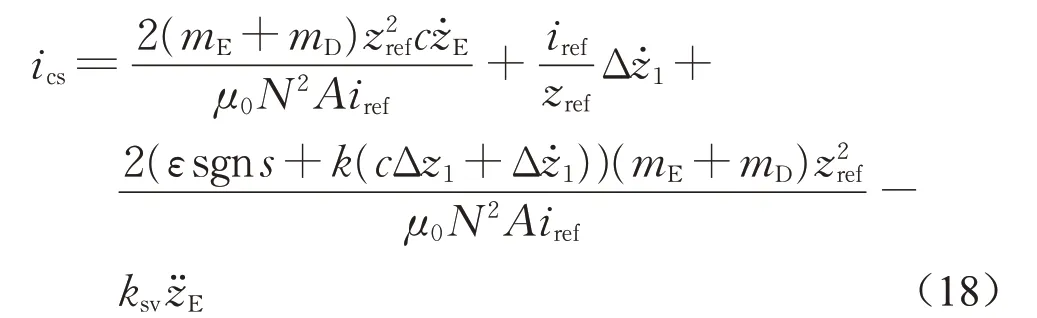
然而,在振动频率过高时式(17)所示控制算法可能出现调整不及时引起的共振问题。另外,这种加速度反馈方法没有学习能力,不能适应多扰动、复杂工况下的悬浮运行。因此,结合径向基函数神经网络进行深度学习来抑制振动。在将轨道视为刚体的前提下采集电磁铁振动变量z¨Eb作为网络输入,控制电流isN作为网络输出,采用1-5-1网络,如图8a所示。将(l-1)时刻的控制电流以及(l-1)时刻和(l-2)时刻的振动加速度作为网络输入,采用如图8b所示的网络进行辨识,得到的网络输出为l时刻的电磁铁振动变量z¨Eb。图8中,q和pi(i=1,2,3)分别为RBFC(radial basis function control)模块和RBFI(radial basis function identification)模块的输入层神经元,hj和wj、bj和vj(j=1~5)分别为RBFC模块和RBFI模块的隐含层神经元及其对应的网络权值,l为离散时间变量。
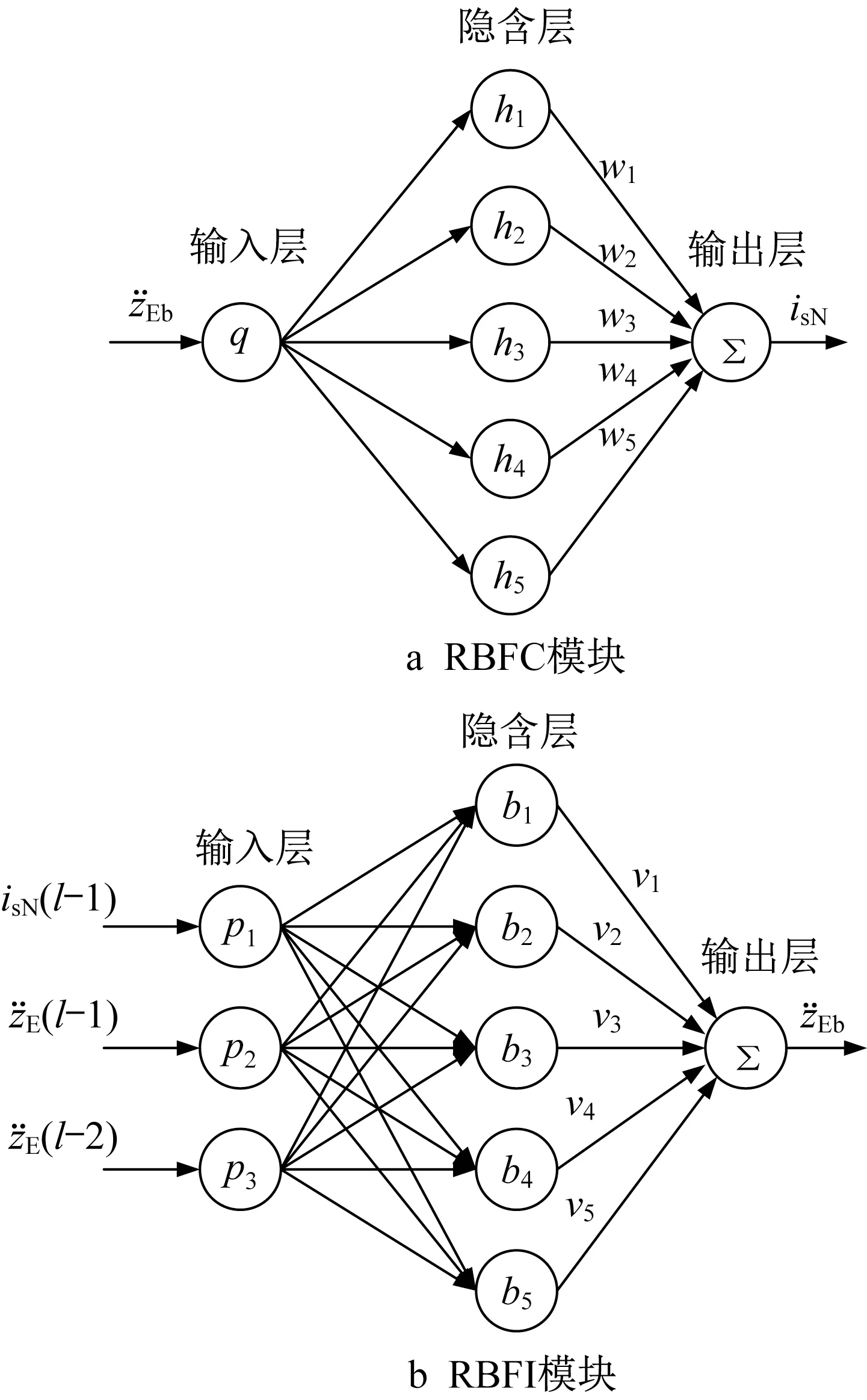
图8 RBF神经网络结构Fig.8 Structure of RBF neural network
图9为基于RBF神经网络的深度学习控制框图。结合如式(2)所示悬浮系统,分别设计了RBFC模块(用于控制)和RBFI模块(用于学习),使系统在复杂的多扰动条件下能够学习并逼近振动期望值(0)从而抑制振动。RBFC模块的输入为电磁铁振动的偏差e¨E。由于理想情况下预期振动为零,因此e¨E=z¨Eb。隐含层的输出用非线性激活函数hj表示,如下所示:
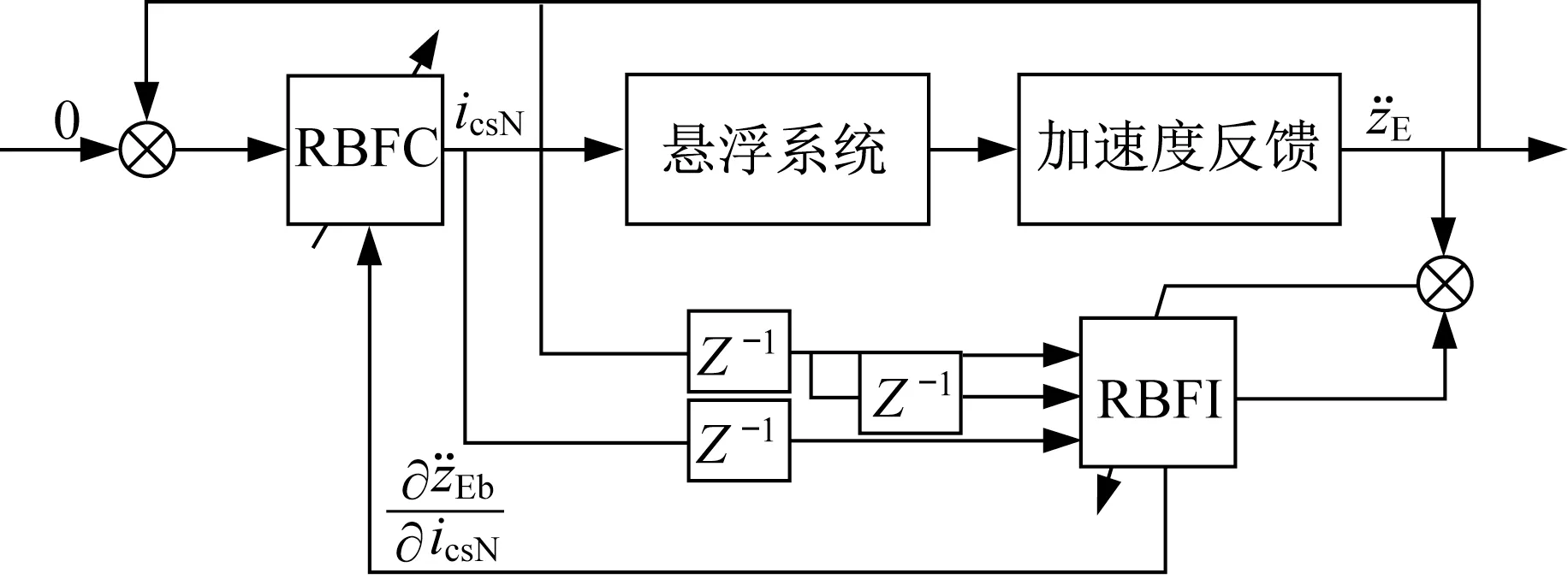
图9 基于RBF神经网络的自适应深度学习振动控制结构Fig.9 Self-adaptive deep-learning vibration control structure based on RBF neural network
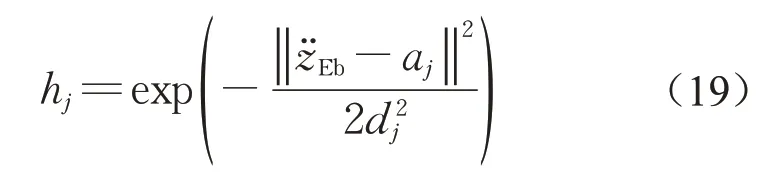
式中:aj为隐含层第j个神经元高斯基函数的中心;dj为隐含层第j个神经元高斯基函数的宽度。
网络的输出抑振电流isN与算法修正后的总控制电流icsN为
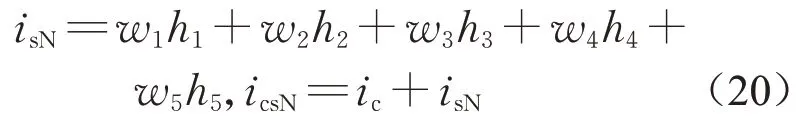
由于控制的目的是使电磁铁在复杂工况下的振动趋于零,因此将性能指标设为网络权值采用梯度下降法进行调整和学习,如下所示:

与所定义的RBFI模块相对应的网络如图8b所示。网络输入对应输出v4b4+v5b5。

式中:ηv为RBFI模块的学习率;αv为RBFI模块的动量因子。由此网络输出电磁铁振动的辨识结果。
3 数值仿真分析
在Matlab/Simulink环境下,基于如式(2)所示的悬浮模型对具有神经网络加速度反馈的滑模控制算法进行验证。
系统参数如表1所示。SMBC-AFC算法中涉及的控制参数可分为2类:一类是SMBC算法中的c和k,另一类是AFC算法(RBF网络)的学习率ηw、ηv和动量因子αw、αv。
根据上述稳定性求解,基于调试经验通过试凑法获得控制参数k=-350,c=0.6,并且定义RBF神经网络参数ηw=0.6,ηv=0.6,αw=0.05,αv=0.05。静态悬浮仿真结果如图10所示。

图10 静态悬浮仿真结果Fig.10 Simulation results of static levitation
在静浮工况下,所提出控制算法(SMBC、SMBC-AFC)和传统PID控制算法均能达到较好的控制效果,0.5 s左右可以达到稳定悬浮状态,并且在较小超调量的同时保证较小的稳态误差。此外,控制电流的响应速度和幅值均在可接受的范围内,与理论计算值基本一致。
列车运行时,负载扰动导致的电磁铁振动使得传感器向控制系统传递的加速度信号发生高频变化,从而影响悬浮间隙,如图11所示。因此,车辆、轨道梁和控制系统构成一个自激振动系统。为了保证悬架的稳定性,采用如式(20)和式(10)所示的控制律进行控制,并且基于RBF神经网络学习权重wj(l)和vj(l)抑制振动。
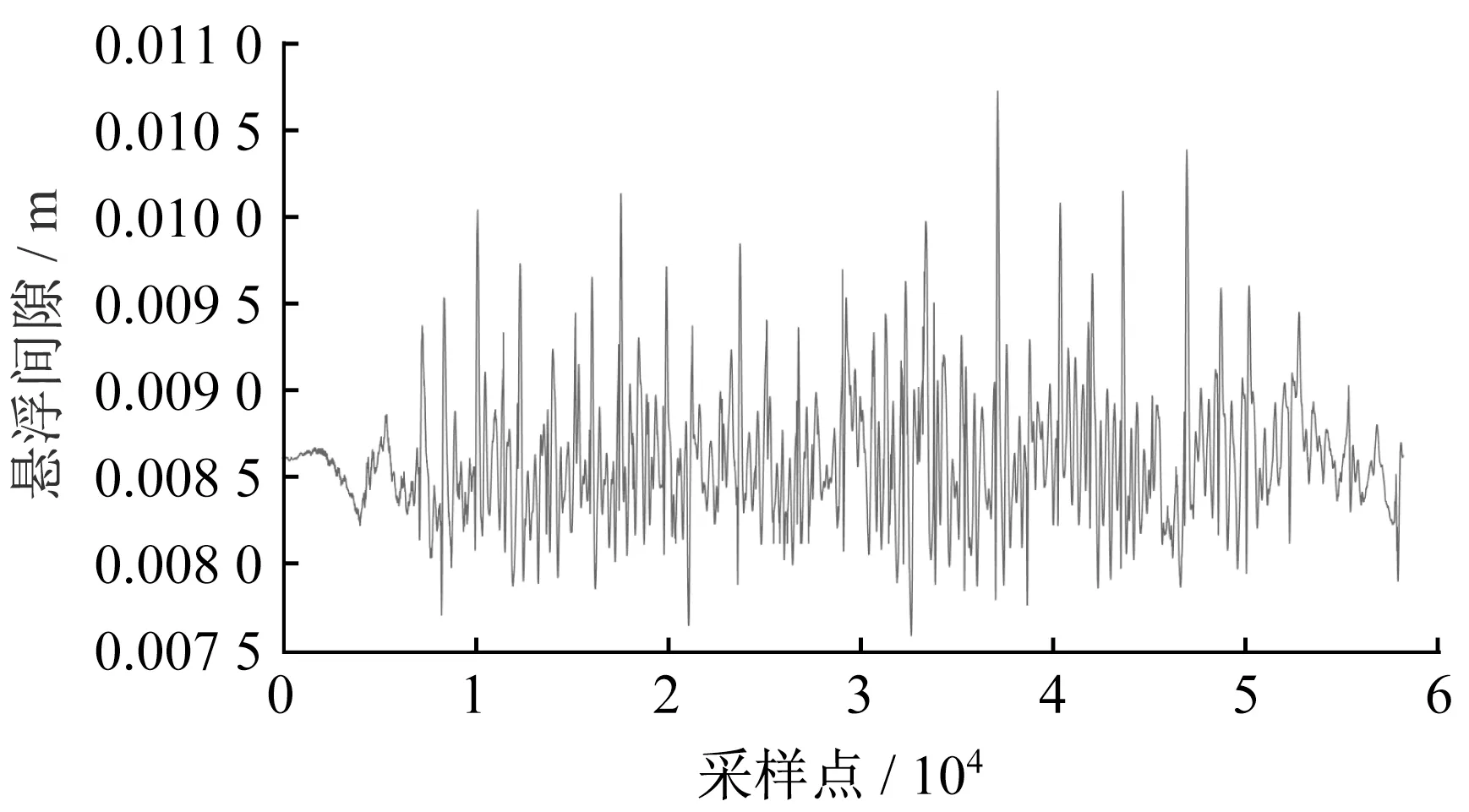
图11 上海临港中低速磁浮试验车运行中的悬浮间隙Fig.11 Suspension gap of Shanghai Lingang medium-low speed maglev test train in operation
由图10可知,系统在0.5 s内稳定悬浮,当时间为3~8 s时,在反馈过程中对系统的输出加速度分别施加幅值为±0.1g、±0.2g、±0.3g的连续随机激励,验证算法的有效性。
不同振动扰动力的控制结果如图12所示。时间t小于3 s时,随机扰动未被激活,垂向悬浮间隙稳定在0.01 m,控制电流维持在20.55 A。当t∈[3,13)s时,在随机扰动激活状态下进行仿真分析。当t∈[3,8)s(SMBC算法控制)时,向电磁铁输入频率为50 Hz的随机加速度扰动,随着扰动幅值的增大,悬浮间隙也逐渐增大。当随机扰动幅值为±0.3g时,电流为33 A,对电流影响较大,不利于悬浮稳定。当t∈[8,13)s(SMBC-AFC算法控制)时,输出悬浮间隙在相同扰动下的稳定性得到显著提高,最大偏差为1.43 mm。
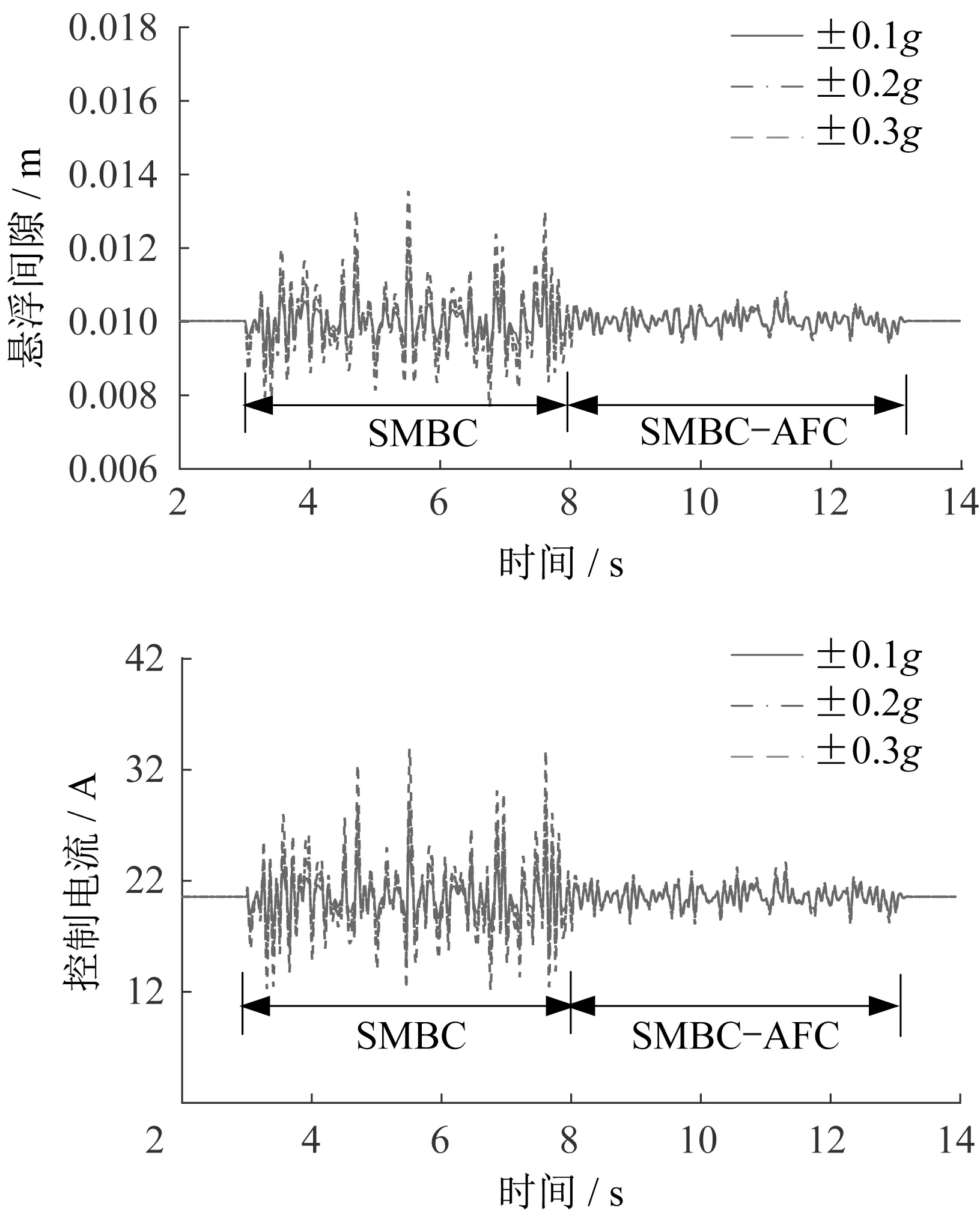
图12 不同振动扰动下的悬浮控制结果Fig.12 Suspension control results under different vibration disturbances
4 试验验证
4.1 试验设计与实施
基于单点悬浮试验台验证所提出控制算法的实际性能。硬件包括电磁铁、负载、固定横梁、dSPACE平台等。悬浮系统由输入/输出(I/O)接口电路、信号传输电路、悬浮控制电路和斩波电路组成。
控制逻辑采用基于现场可编程逻辑门阵列(FPGA)的Verilog语言编写,悬浮控制逻辑如图13所示。在Simulink平台编写控制算法,并基于dSPACE仿真系统实现实时控制。单点悬浮试验台控制结构框图如图14所示。
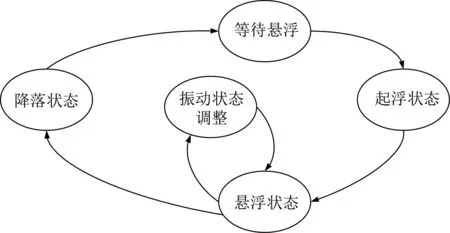
图13 悬浮控制逻辑结构Fig.13 Levitation control logic structure
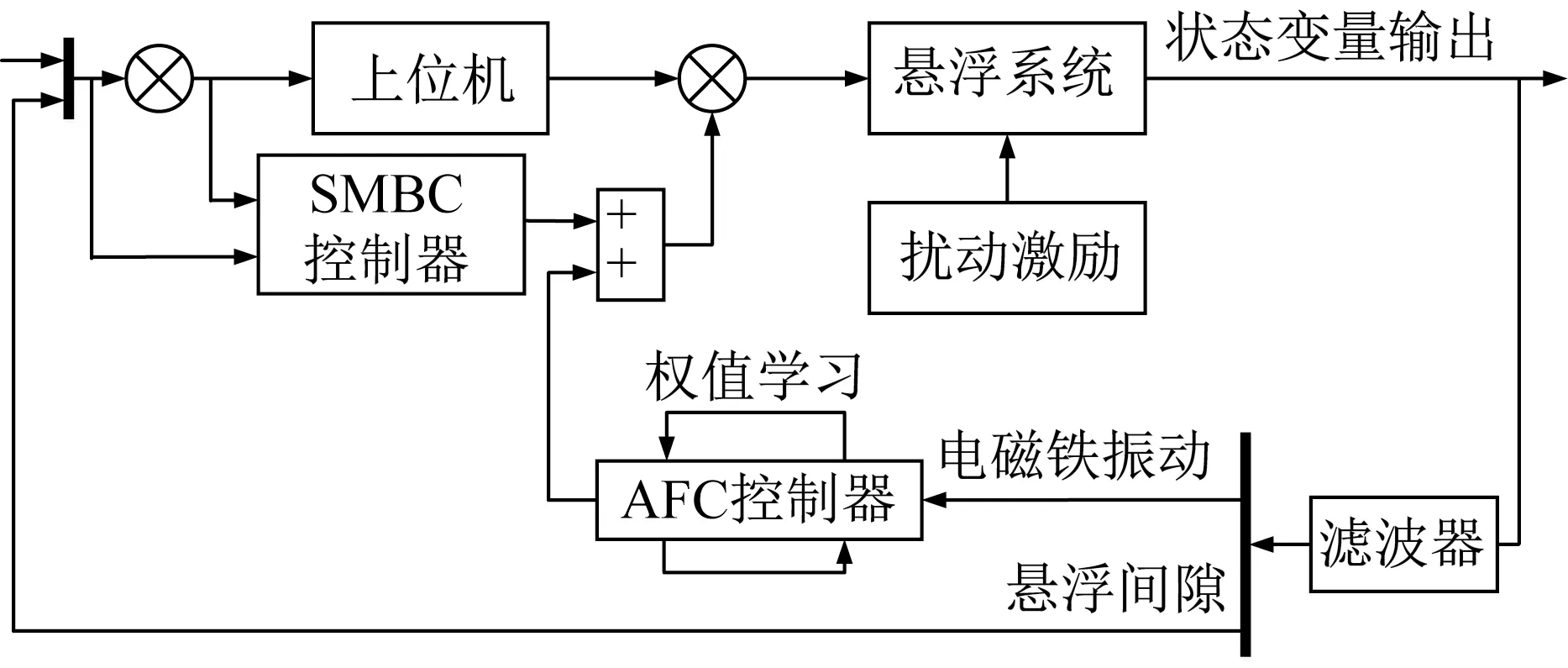
图14 单点悬浮试验台控制系统结构框图Fig.14 Block diagram of control system structure for single-point suspension test platform
4.2 结果分析
基于单点悬浮试验台的静态悬浮初步试验结果如图15所示。
如图15a、b所示,在静态悬浮过程中,3种控制算法都能达到很好的控制效果,响应速度快,静态误差小。所提出的SMBC算法和SMBC-AFC算法可以进一步加快响应速度,减小超调。稳定悬挂后,悬浮间隙为10.015 mm。所提出的算法能够降低大电流的影响(PID算法控制下的峰值电流为24.14 A,SMBC和SMBCAFC算法控制下的峰值电流为20.71 A),比PID控制算法更能保证系统的安全性。
电磁铁的振动加速度如图15c所示。在不进行悬浮操作时(t<2 s),由于系统已通电,在电磁线圈影响下,加速度传感器接收到的振动信号有电磁干扰,在悬浮稳定时(t>2.3 s),接收到的信号同样受到电磁干扰影响。此时,传输给控制算法的信号可能会导致悬架间隙跟踪不准确等问题。从图15c的比较可以看出,所提出的算法不仅可以有效地降低电磁铁在浮动过程中的加速度峰值,还可以滤除电磁干扰(因为本试验是静态悬浮,不需要抑制电磁振动),从而提高悬浮间隙跟踪的精度。
由于列车的悬浮过程处于静态悬浮阶段,因此假设动态扰动忽略不计。在进一步研究动态扰动对系统的影响时,只对稳定悬浮后的部分进行分析。
如图15所示,模拟时间t设定为12 s,当t=2 s时,按下悬浮指令,当t=4 s时,系统将达到稳定悬浮状态(为保证试验的准确性,预留2 s作为悬浮间隙的动态调整时间),因此只分析t∈[4,12]s的输出。
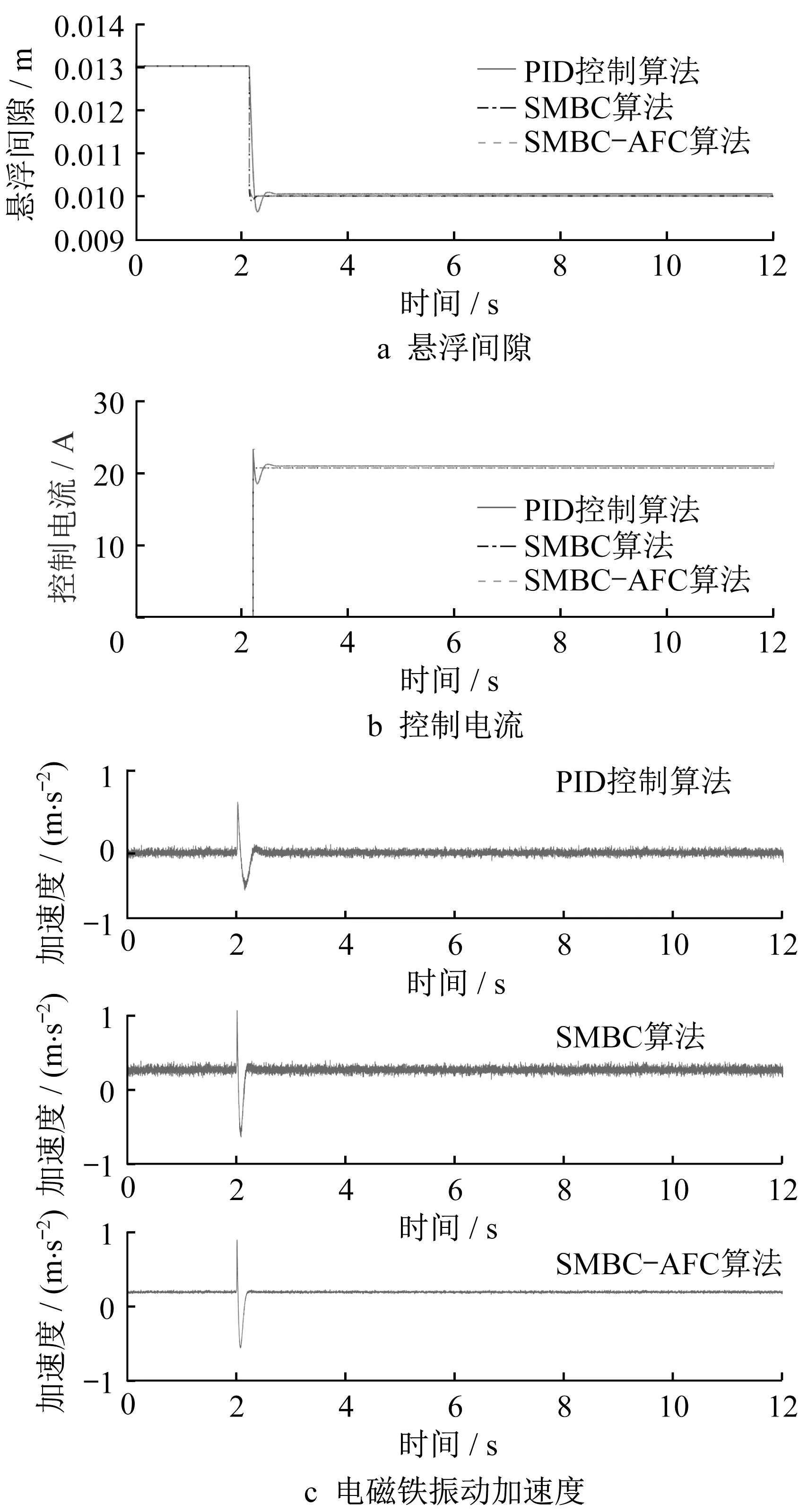
图15 不同算法下的悬浮控制结果Fig.15 Suspension control results under different algorithms
悬浮稳定后,在5 s<t<9 s时输入正弦扰动(扰动频率5 Hz,幅值±2 mm),试验结果如图16所示。
由图16b可以看出,当在5 s施加扰动时,PID算法控制下的悬浮间隙经过多次被动调整后无法收敛。在扰动激发过程结束前(7.45 s)被迫降落,试验过程结束。此时,电流和加速度趋于零。这说明系统在处于大扰动环境下PID控制算法的鲁棒性较弱。为了说明所提出算法的有效性,在相同条件下进行了试验,结果如图16a所示。当5 s<t<9 s时,产生小范围内等幅振动。虽然存在一个极限环,但是当扰动结束时,系统迅速收敛到悬架位置,电磁铁振动得到有效抑制。此外,结合图16a可以看出,带加速度反馈的SMBC-AFC算法比SMBC算法具有更强的鲁棒性。
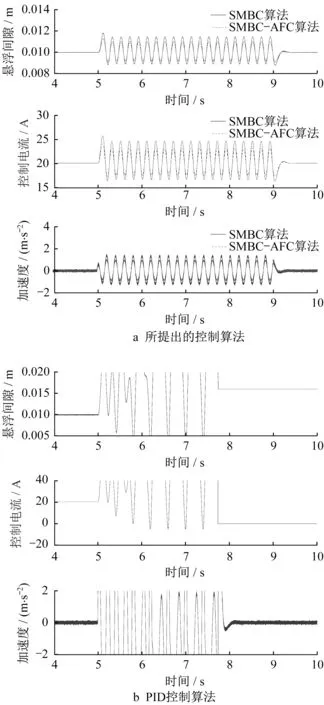
图16 扰动环境下试验结果Fig.16 Experimental results in disturbed environment
5 结语
针对动态悬浮过程中外部振动激励问题,以电流控制最小悬浮单元为基础,提出了一种带加速度补偿的滑模控制算法。基于指数趋近律设计相关滑模控制算法,并通过稳定性分析确定滑模参数可调范围。此外,针对RBF神经网络的自学习功能,提出了AFC算法作为SMBC算法的补充,并对控制系统的几种典型工况进行试验分析,验证其有效性。结果表明,SMBC-AFC算法可提高系统在复杂条件下的鲁棒性,大大减少系统的抖振现象,同时降低浮充初期电流峰值,提高了设备的安全性。然而,当SMBC算法应用于其他非线性系统时,需要根据实际模型进行稳定性分析,从而确定控制参数。另外,需要结合模型阶数和神经元个数来确定AFC算法的网络结构。

