考虑涡流效应的端部悬浮系统建模与控制器优化设计

翟明达，龙志强，李晓龙，丁菁芳，张 博

（国防科技大学智能科学学院，湖南长沙410073）

中低速磁浮列车作为一种新型轨道交通制式，具有运行安全、噪声低，线路适应性强，建设和维护成本低，舒适度高等众多优势［1-2］。近年来中低速磁浮列车受到国内外众多城市的关注和青睐，发展前景十分广阔，长沙磁浮快线、北京磁浮S1线已经安全载客运营多年，清远磁浮线、凤凰磁浮线即将开通运营［3］。随着国内外多条商业运营线路的开通，人们开始认识到中低速磁浮列车作为新型轨道交通制式的技术优势，磁浮列车也成为轨道交通领域技术研究和发展的热点和焦点［4］。然而，中低速磁浮列车高速运行时，端部悬浮电磁铁受涡流效应影响明显，气隙磁通密度分布发生显著改变，悬浮间隙波动也随之加剧。涡流效应给端部悬浮系统带来的不确定性提升了悬浮控制的难度，导致端部悬浮单元的悬浮性能明显低于其他悬浮单元。Ohsaki等［5］以日本HSST（high speed surface transport）型磁浮列车为研究对象，对轨道中的涡流进行了数值计算，Yamamura等［6］分析了涡流效应作用下的气隙磁场和悬浮力，但是这些研究都集中在涡流效应的数值计算与影响分析，缺乏从悬浮控制角度去分析涡流效应带来的模型不确定性，也没有给出动态运行条件下端部悬浮电磁铁的鲁棒性和抗干扰能力下降的解决办法。

为了克服涡流效应对端部悬浮系统的不利影响，首先对涡流效应的原理进行分析，采用Maxwell软件建立与实际系统比例相同的有限元模型并对悬浮电磁场进行数值仿真，解析端部涡流效应对悬浮电磁力的影响。结合列车运行过程中悬浮系统的动态特性，建立考虑涡流效应的端部悬浮系统模型，并依据模型特性设计标称控制器。针对列车高速运行时端部悬浮系统的鲁棒性和抗干扰能力下降问题，提出一种不改变现有标称控制器结构的参数优化算法，通过动态调整控制参数，实现对现有标称控制器的动态调整与优化设计。

1 中低速磁浮列车悬浮系统结构与工作原理

中低速磁浮列车车辆总体结构分为上下2层，以车厢为主的上层结构与轮轨列车车辆基本相同，以悬浮架以及悬浮系统为主的下层结构与轮轨列车车辆完全不同。车厢与悬浮架之间通过空气弹簧相连。1节完整的中低速磁浮列车车辆由5个悬浮架构成，每个悬浮架共有4个悬浮单元。每个悬浮单元为一套完整的悬浮控制系统，由悬浮电磁铁、悬浮控制器以及悬浮传感器组成，其中悬浮电磁铁为整个系统的被控对象。中低速磁浮列车总体结构如图1所示。

图1 中低速磁浮列车总体结构Fig.1 Overall structure of medium-low speed maglev train

众所周知，同性磁极相互排斥，异性磁极相互相吸，中低速磁浮列车悬浮系统就是利用悬浮电磁铁与导轨间的相互吸引实现磁浮列车的稳定悬浮。中低速磁浮列车车厢底部共有20组悬浮电磁铁，悬浮电磁铁通电后产生可控电磁场，从而产生向上的电磁力。悬浮控制器通过动态调整悬浮电磁铁中电流大小，使其产生的电磁力与列车负载实现动态平衡。悬浮传感器安装在悬浮电磁铁上，实时检测悬浮电磁铁与轨道面的距离，并发送量测数据给悬浮控制器。悬浮控制器收到量测数据后与给定值进行比较，计算出对应的控制量并作用于悬浮电磁铁，从而保证悬浮电磁铁始终工作在设定间隙。中低速磁浮列车悬浮系统结构如图2所示。

图2 中低速磁浮列车悬浮系统结构Fig.2 Structure of magnetic levitation system in medium-low speed maglev train

2 涡流效应原理与数值分析

根据法拉第电磁感应定律，当导体相对于磁场运动时或者导体处在变化的磁场中时，导体感应出电动势从而形成涡旋电流，简称涡流。当磁浮列车沿着轨道高速向前运行时，悬浮电磁铁与导轨之间建立的闭合磁场沿着轨道运动，不断形成新的闭合磁场，因此导轨中产生涡流。磁浮列车的导轨为非叠层钢轨，悬浮电磁铁与导轨之间的快速相对运动形成的涡流会阻碍其相对运动。在悬浮电磁铁模块前端，由于磁场处在增强的变化趋势中，涡流效应会产生一个相反的磁场，从而阻止导轨中磁场强度的增大；在悬浮电磁铁模块末端，涡流效应会阻止导轨中磁场强度的减小。

涡流效应发生时F型导轨的磁场方向如图3所示。图3中，虚线箭头所指的方向为悬浮电磁铁气隙磁场的磁感应强度方向，实线箭头所指的方向为涡流效应产生的涡流磁场的磁感应强度方向，悬浮电磁铁气隙磁场方向与涡流磁场方向完全相反。悬浮电磁铁模块前端的涡流效应导致悬浮电磁铁与导轨之间气隙磁通减弱，而末端的涡流效应对气隙磁场影响较弱，因此端部悬浮电磁铁的整体悬浮能力出现下降趋势。

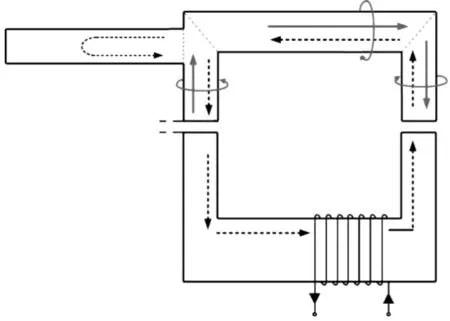
图3 涡流效应原理示意图Fig.3 Schematic diagram of eddy current effect principle

利用有限元法进一步分析涡流效应特性，对悬浮电磁铁的电磁场进行数值仿真。通过Maxwell软件建立与实际系统比例相同的三维有限元模型，参照长沙磁浮快线悬浮电磁铁以及F型导轨的结构、尺寸和参数，对悬浮电磁铁模块的涡流效应进行数值分析。F型导轨、悬浮电磁铁内部铁芯以及外围极板的材料均为Q235B，三维模型如图4所示。

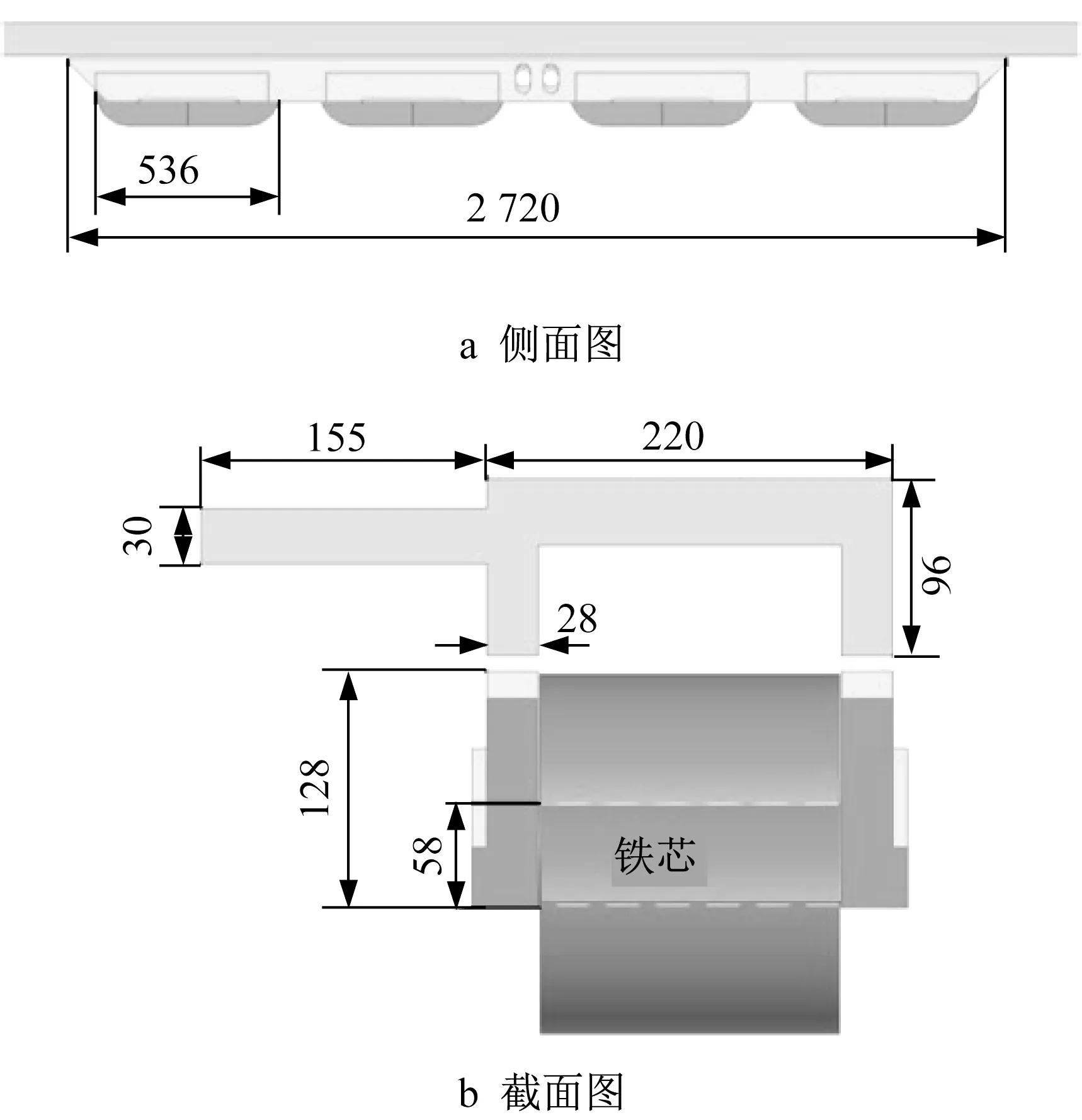
图4 悬浮电磁铁与F型导轨的三维模型（单位：mm）Fig.4 Three-dimensional model of electromagnet and F-type track(unit:mm)

首先，为建立的悬浮电磁铁与F型导轨的三维模型选择求解场、定义边界并建立运动区域；其次，在三维仿真中对建立的模型添加激励、划分网格（见图5），并设置运动的模式、方向、距离和速度［7］。

中低速磁浮列车左右两侧分别有10组悬浮电磁铁，为了研究中低速磁浮列车高速运行时涡流效应对端部悬浮电磁铁与非端部悬浮电磁铁的影响，对不同速度下的悬浮气隙磁场进行计算，如图6所示。结果表明，涡流效应对端部悬浮电磁铁与非端部悬浮电磁铁的影响完全不同，涡流效应只会对沿着运行方向的端部悬浮电磁铁产生剧烈影响，速度越快，气隙磁通下降越明显，对悬浮力的影响也就越大。根据涡流效应原理，沿着导轨运行方向的第一组悬浮电磁铁会迅速磁化导轨，而剩余的9组悬浮电磁铁通过时，磁场变化已经很小，导轨涡流效应的影响也会变弱。

图6 不同速度下端部悬浮电磁铁与非端部悬浮电磁铁的磁通密度Fig.6 Magnetic flux density of front and another electromagnets at different speeds

高速运行中的端部悬浮电磁铁受涡流效应的影响更为明显，气隙磁通密度的分布发生了明显改变，为了保证悬浮电磁铁始终工作在设定悬浮间隙，端部悬浮电磁铁局部极易发生磁场饱和。在涡流效应的作用下，端部悬浮电磁铁为了提供足够的悬浮力，必须提高悬浮电流，从而降低悬浮控制系统的鲁棒性，悬浮间隙波动也变得更为剧烈。

通过对比不同速度下数值结果后发现，涡流效应对端部悬浮电磁铁悬浮力造成的影响主要与列车的速度有关。不同速度下导轨中的涡流密度计算结果如图7所示，速度越快，导轨中形成的涡流密度越大，对悬浮力的影响也越大。

图7 不同速度下轨道涡流密度Fig.7 Eddy current density of the rail at different speeds

3 考虑涡流效应的端部悬浮系统建模与控制器优化设计

为克服涡流效应对端部悬浮系统的不利影响，基于对涡流效应原理以及数值仿真结果的分析，结合列车运行过程中悬浮系统的动态特性，建立考虑涡流效应的端部悬浮系统模型，并依据模型特性设计标称控制器。针对列车高速运行时端部悬浮系统的鲁棒性和抗干扰能力下降问题，提出一种不改变现有标称控制器结构的参数优化算法，通过动态调整控制参数，实现对现有标称控制器的动态调整与优化设计。

3.1 考虑涡流效应的端部悬浮系统建模

为了描述悬浮系统输入量与输出量之间的关系，需要建立相应的数学模型。对于中低速磁浮列车悬浮系统这个复杂的机电系统，在建立系统模型时为了降低微分方程阶次，降低求解难度，往往会忽略很多因素。本研究中也忽略了漏磁和边缘效应，认为磁势全部均匀降落在悬浮间隙上。悬浮系统模型如图8所示。图8中，φ为磁通，u为电压，i为电流，m为悬浮电磁铁等效质量，M为车厢的等效质量，z为悬浮电磁铁的绝对位移。悬浮电磁铁的绝对位移z与悬浮间隙c相等。

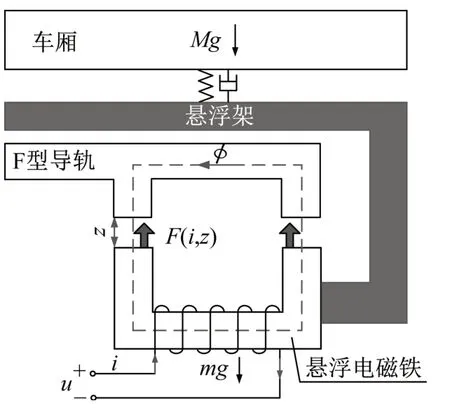
图8 悬浮系统模型Fig.8 Magnetic levitation system model

考虑到列车的实际运行工况，涡流效应直接导致端部悬浮电磁铁的气隙磁场以及悬浮力下降，极大地降低了端部悬浮系统的鲁棒性，以往的建模过程忽略了涡流效应的影响，从而导致端部悬浮电磁铁悬浮间隙波动剧烈，因此端部悬浮系统建模过程中必须要考虑涡流效应的影响。由麦克斯韦方程组得到轨道中涡流密度，如下所示：

式中：J为轨道中涡流密度；E为电场强度；v为运行速度；B为磁感应强度；μ为磁导率；σ为电导率［8］。基于安培环路定理，可以采用分离变量法来求解偏微分方程，进而获取涡流效应下的磁感应强度。磁力线垂直于悬浮电磁铁表面且稳定，设面积为S，真空磁导率为μ0，则电磁力F(i，z)的表达式为

综所述上，涡流效应影响下电磁力的解析表达式为

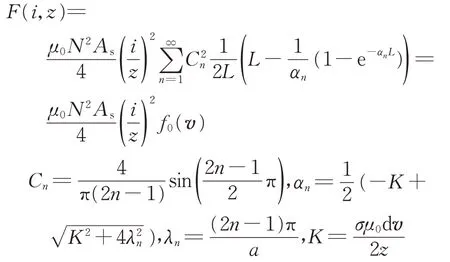
式中：N为线圈的匝数；As为悬浮电磁铁的有效磁极面积；L为电磁铁模块长度；f0(v)为端部涡流效应系数，是一个关于速度的函数；a为磁极宽度。

悬浮电磁铁是一个电感性元件，因此其电压与电流的关系式为

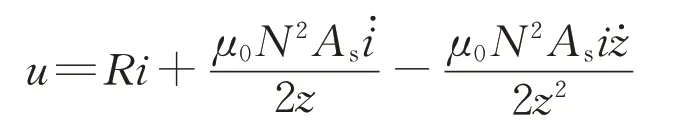
式中：R为悬浮电磁铁电阻。此时，悬浮电磁铁的动力学方程可以表示为

中低速磁浮列车悬浮系统的参数如表1所示。

表1 中低速磁浮列车悬浮系统参数Tab.1 Parameters of magnetic levitation system for medium-low speed maglev train

3.2 悬浮标称控制器的设计

中低速磁浮列车悬浮系统模型中存在平方项等非线性环节，因此悬浮系统是一个典型的非线性系统。通过非线性微分方程组求解来分析悬浮系统性能非常困难，但中低速磁浮列车悬浮系统工作点稳定，工作区间集中在工作点附近，并且不存在本质的非线性环节，因此可以通过线性方法来分析非线性悬浮系统的动态特性。

对于非线性的中低速磁浮列车悬浮系统，整个系统在平衡点处的边界约束条件为

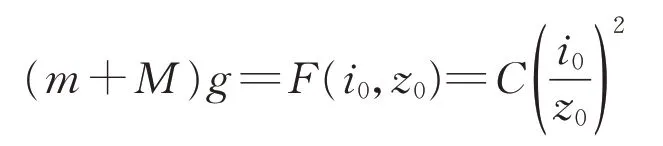
式中：i0为悬浮电磁铁在平衡点处的稳态电流。此时可以得到悬浮系统的线性化模型，如下所示：

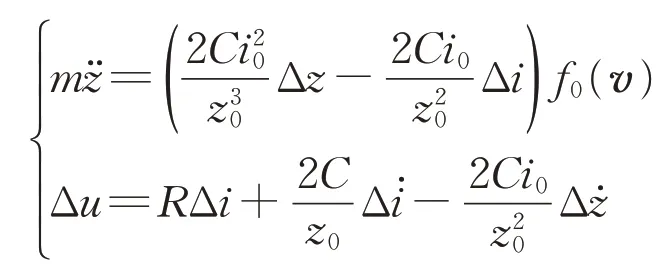
选取状态变量x=(x1，x2，x3)T=(Δz，Δz˙，Δi)T，线性化化后悬浮系统的状态空间表达式为

悬浮系统特征多项式不满足Hurwitz稳定性判据，依据Hartman-Grobman定理，悬浮系统是不稳定的。进一步分析系统的可控性，悬浮系统的可控性矩阵秩为3，因此悬浮系统完全可控。

为了使悬浮系统能够工作在期望状态，需要设计相应的控制律。在工业和交通控制领域，比例-积分-微分（PID）控制算法是最成熟也是应用最为广泛的控制算法。基于串级控制的思想，悬浮控制算法通常分为2个部分，即内环为电流环，外环为位置环［9-10］。当悬浮电磁铁工作在平衡位置时，其电感只在极小范围内变化，此时悬浮电磁铁的电感可以认为是一个常量。因此，在工作点附近，悬浮电磁铁电压和电流的变化关系表示为

对式（1）进行拉氏变换，传递函数

式中：s为频域。悬浮电磁铁电压和电流的传递函数表明，悬浮电磁铁是一个典型的惯性环节，输出电流的响应速度严重滞后于输入电压的变化速度。悬浮电磁铁响应时间太长，无法满足悬浮控制系统的响应速度要求，为此在悬浮控制算法的设计中引入了电流负反馈，如图9所示。图9中，kc1为前置放大倍数，kc2为负反馈系数。

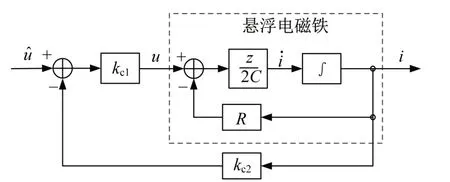
图9 电流负反馈动态结构Fig.9 Current negative feedback dynamic structure

引入电流反馈前的输入电压，则直接作用于悬浮电磁铁上的电压

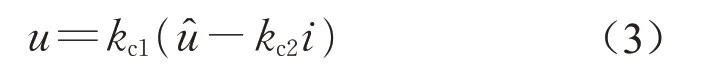
当输入电压为单位阶跃信号时，引入电流环后的响应曲线如图10所示。

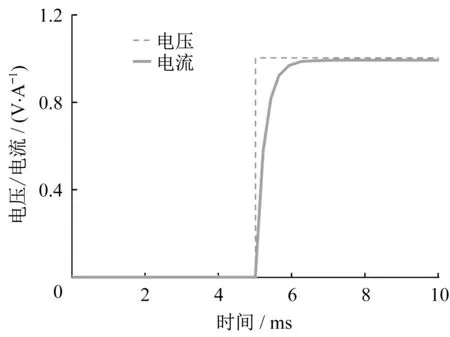
图10 悬浮电磁铁的阶跃响应曲线Fig.10 Step response curve of the electromagnet

引入电流负反馈后，输出电流能够快速跟踪输入电压的变化，同时在悬浮系统的频带内，电压与电流的比例系数近似等于1。悬浮系统的阶次由3阶降为2阶。电流环设计完成后，位置环的设计采用PID控制算法，计算式如下所示：

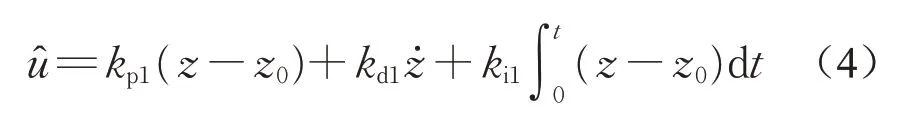
式中：kp1为比例系数增益；kd1为微分系数增益；ki1为积分系数增益。此时，悬浮系统的最终控制律可以表示为

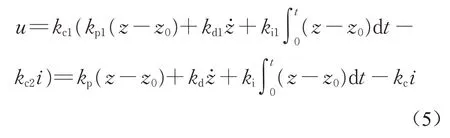
式中：kp为标称控制器的比例反馈系数；kd为标称控制器的微分反馈系数；ki为标称控制器的积分反馈系数；kc为标称控制器的电流反馈系数。

标称控制器设计完成后，为了评估其性能，利用Simulink搭建非线性悬浮系统模型并且进行动态仿真。中低速磁浮列车悬浮系统控制框图如图11所示。

图11 悬浮控制系统框图Fig.11 Block diagram of magnetic levitation control system

悬浮电磁铁的初始间隙为25 mm，目标间隙设定为10 mm。当悬浮系统收到起浮命令时，悬浮电磁铁的动态响应如图12所示。悬浮电磁铁在标称控制器作用下最终稳定在设定间隙，在整个起浮过程中，悬浮电磁铁在标称控制器作用下状态稳定且可控。

图12 悬浮电磁铁的悬浮间隙Fig.12 Suspension gap of the electromagnet

3.3 悬浮控制器的优化设计

为了应对列车实际运行过程中的各种工况、路况条件，中低速磁浮列车悬浮系统的控制问题研究也要考虑系统的鲁棒性以及适应能力［11-13］，因此对悬浮控制系统的精度、响应速度以及应对外界扰动的抗干扰能力都提出了更高要求。尤其对于端部悬浮电磁铁，在涡流响应的作用下表现出鲁棒性差、抗干扰能力弱的特性。为了提高端部悬浮电磁铁的鲁棒性，在不改变现有标称控制器结构的基础上进一步优化设计。

在标称控制器电流环的设计中，电流负反馈的作用是提高系统的响应速度，使得输出电流能够快速跟踪输入电压。然而，电流负反馈存在的同时也抑制了电压的快速增加。当悬浮电磁铁受到方向向下的干扰力时，为了增大电磁力，悬浮电磁铁的电流将从初始时的i1增大到i2（i2＞i1），此时电流负反馈通道产生的控制量将由-kci1缩小为-kci2。悬浮控制系统的控制目标是通过增加控制电压来加大电磁力，此时电流负反馈的存在不利于悬浮电磁铁抵御外界干扰。

为提高悬浮系统抵御外界干扰的能力，快速增加控制电压来加大电磁力，标称控制器的电流环就需要重新优化设计。既能提高电流响应的速度，保障输出电流能够快速跟踪输入电压，又要在系统受到干扰时快速增加电压来增大电磁力。基于上述分析，重新设计电流负反馈系数。电流反馈系数可以通过悬浮间隙的波动情况进行动态调节，计算式如下所示：

式中：kcopt为优化后的电流反馈系数；pc为可调因子。

优化后的悬浮控制器电流反馈系数能够在列车受到干扰偏离平衡位置时，通过主动减小电流负反馈系数来加快电压增加的速度。为保障悬浮系统的响应速度，电流反馈系数必须控制在一定范围之上，因此优化后悬浮控制器的电流反馈系数kcopt被设定为

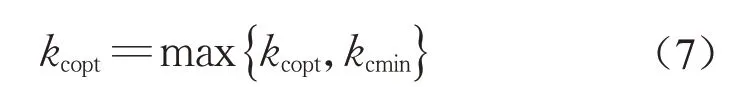
式中：kcmin为满足悬浮系统响应速度要求的最小反馈系数。

标称控制器位置环的设计中，系统的控制目标是在确保悬浮系统稳定的基础上尽最大可能提高系统的抗干扰能力。通过增大比例反馈系数kp来增加系统刚度，改善系统的鲁棒性，但是比例反馈系数增大到一定程度会直接导致系统失稳。因此，标称控制器位置环中的比例反馈系数就需要重新优化设计，在参数的选取时要综合各方面的要求，计算式如下所示：

式中：kpopt为优化后的比例反馈系数；pp为可调因子。

当悬浮系统工作在平衡点附近时，比例反馈系数保持不变。当悬浮系统偏离平衡点时，为提高系统的抗干扰能力，通过增大比例反馈系数来增加悬浮系统刚度。

综上所述，优化后的控制律为

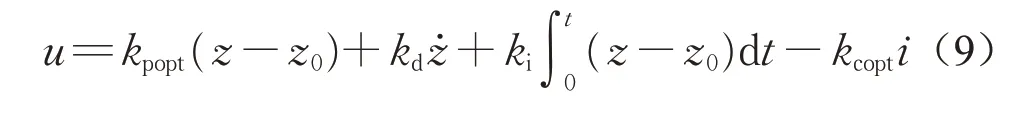
4 仿真验证与试验

为检验悬浮系统的抗干扰能力，对中低速磁浮列车悬浮系统在外力扰动下的动态响应进行仿真。当悬浮系统处在正常悬浮状态时，对悬浮系统施加扰动，15 s时受到方向向下的5 kN阶跃干扰力，持续3 s，悬浮系统的悬浮间隙波动如图13所示。

为进一步检验悬浮系统的抗干扰能力，当悬浮系统处在正常悬浮状态时，对悬浮系统的悬浮间隙测量通道施加幅值为1.5 mm的阶跃干扰，持续时间为2 s，此时悬浮系统的悬浮间隙如图14所示。

由图13和图14可知，悬浮系统在受到扰动干扰时，悬浮间隙都会出现一定波动，但是采用标称控制器的悬浮系统波动更为剧烈，这是因为当列车受到干扰偏离平衡位置时，优化后的控制器能够通过主动调整控制系数来抵御外界扰动影响，悬浮系统的鲁棒性和抗干扰能力得到了显著提升。

为了克服涡流效应对高速运行过程中端部悬浮电磁铁的不利影响，将优化后的控制器应用于长沙磁浮快线，检验实际运行过程中悬浮系统的抗干扰能力。在长沙磁浮快线正线开展高速运行测试，通过车载CAN（controller area network）总线收集并记录了端部悬浮电磁铁运行过程中的悬浮间隙，如图15所示。

图15 端部悬浮电磁铁的悬浮间隙与速度Fig.15 Suspension gap and speed of front electromagnet

试验测试结果表明，在整个速度区间内悬浮间隙波动均在合理范围。即使在高速区间，在涡流效应的不利影响下，通过动态调整控制参数，端部悬浮系统在优化后的控制器调节下也能表现出良好的鲁棒性和抗干扰能力。

5 结语

为了克服涡流效应的不利影响，首先分析和讨论了涡流效应原理，通过Maxwell软件建立了与实际系统比例相同的有限元模型并对端部悬浮电磁铁的电磁场进行了数值仿真。结果表明，高速运行过程中的端部悬浮电磁铁受涡流效应影响，气隙磁通密度的分布发生了明显改变，严重影响了悬浮电磁力的生成。因此，建立了考虑涡流效应的端部悬浮系统模型，并依据模型特性设计了标称控制器。在不改变现有标称控制器结构的基础上，实现了对现有标称控制器的动态调整与参数优化，提高了悬浮系统鲁棒性和抗干扰能力。优化后的控制器已成功应用于长沙磁浮快线，实际运行数据表明端部悬浮电磁铁的鲁棒性和抗干扰能力得到了显著提升。