基于向量式有限元法的磁浮列车磁力耦合系统建模与数值分析
孙友刚,徐俊起,王素梅,袁 野,倪一清
(1.同济大学铁道与城市轨道交通研究院,上海201804;2.同济大学国家磁浮交通工程技术研究中心,上海201804;3.香港理工大学国家轨道交通电气化与自动化工程技术研究中心香港分中心,香港999077;4.江苏大学电气信息工程学院,江苏镇江212036)
电磁悬浮(EMS)型磁浮列车是一种新型轨道交通工具,具有无接触、无摩擦、噪声低、易维护等优点[1-3]。近年来,我国磁浮交通尤其是低速磁浮交通得到迅猛发展,但在大规模商业化前,磁浮交通技术仍存在诸多亟待解决的问题,如磁浮控制系统可靠性、磁浮车辆的承载力、车-轨耦合作用机理等[4-5]。其中,磁浮列车的车-轨耦合模型如何更加准确地反映磁浮交通的特征和机理,一直困扰着磁浮技术专家和工程师。磁浮交通的轨道梁多为高架结构,目前大部分磁浮车-轨耦合建模方法要么忽略或简化非线性项,电磁力线性化后类似弹簧阻尼器(失去本质特征),要么只建立在轨道梁某个位置的静态悬浮(不能反映列车速度影响)。因此,亟需研究由可控电磁力无接触耦合的车-轨动力学机理,建立反映不同速度下车辆和轨道垂向运行动态特性的计算模型。
在早期磁浮列车动态特性研究中,将磁浮列车简化为轨道上的一个移动力[6]或者移动质量[7],但是这样的模型无法反映车辆的动力学行为。翟婉明等[8]和赵春发等[9]同时考虑车辆系统和轨道系统,提出了用弹簧阻尼器替代多电磁铁磁浮的车-轨耦合模型。然而,将电磁力简化为弹簧阻尼器虽然提高了计算效率,但是不能完全反映电磁力的非线性特征。Yau[10]考虑比例-积分(PI)控制器下的非线性电磁力,将磁浮列车简化为一系列考虑二系悬挂系统的二自由振子模型,其中轨道被简化为单跨的欧拉梁。每个振子间没有任何连接,并且不能研究车辆的点头等运动状态。Han等[11]提出了一种基于多体动力学的磁浮车辆动力学模型,该模型考虑了分段开关轨道的灵活性。利用所建立的分析模型,进行了中低速下悬浮稳定性和安全性的仿真研究。Han等[12]基于多体动力学开发了EMS型磁浮列车系统集成模型,分析了列车沿曲线运行时侧风的影响和横向阻尼器的影响。Zhang等[13]设计了低动力作用下的新型中低速磁浮列车悬浮架,并进行了动力学数值仿真验证。对于电磁力控制环节仿真,采用了简化的线性磁力控制模型。Sun等[14]建立了EMS型磁浮列车的车-轨耦合动力学模型,研究了车-轨耦合共振的发生机理,但是未考虑动态跑车过程。近些年,学者们[15-16]利用成熟的商业有限元软件进行轨道建模,再联合其他软件模块组成联合仿真模型,大大提高了精确度,但是大量的网格和多个软件成本增大了计算负担和花费,并且无法提供数学模型给控制器设计使用。
综上,EMS型磁浮列车系统的车-轨动力学耦合机理和模型研究已取得较大进展,但是对不同速度和电磁力非线性共同作用下的动态跑车过程仍然研究不足。就磁浮车辆行驶在桥梁上的运动而言,涉及到2个子系统的相互耦合问题,而且这种耦合行为会随着时间的变化而改变。简化的模型不能完全反映耦合特性,而传统有限元在分析磁浮列车车-桥的动力耦合行为时计算又非常耗时。向量式有限元法是以向量式力学为基础的新型有限元计算方法。该方法通过数值计算的方式来准确预测和分析结构的真实运动行为,还可以用来分析大变形、大变位、断裂、多体运动等复杂行为。采用点值描述的方式,将连续结构体以一组有限的质点来描述,每个质点可以独立且并行计算,故该方法可以用来分析多个运动变形体的相互作用。基于此,将向量式有限元法作为一种更加简单高效的计算方法进行磁浮列车车-桥耦合作用分析。
针对上述问题,首先推导出磁浮列车的磁力耦合模型,其中高架轨道模型采用向量式有限元法。然后,以梁的跨中位移、梁端转角、振动加速度以及悬浮间隙偏差为重要指标,对不同车速下的磁浮列车动态通过轨道梁的过程进行仿真分析。最后,利用上海临港中低速磁浮基地的全尺寸试验样车,对该建模方法的准确性和有效性进行初步验证。
1 磁浮列车磁力耦合模型
以向量式有限元法进行车-桥动力学分析时,可采用点值描述法将车辆和桥梁用一组质点表示,每个质点均满足牛顿第二定律。作用在车辆上的外力以及作用在桥梁上的外力为悬浮力的作用力和反作用力,施加在桥梁上每个质点的内力可以由梁单元的逆向运动得到。
如图1所示,一节磁浮列车以匀速v行驶在简支梁上。车体由1个车厢、5个悬浮架组成。每个悬浮架有2个电磁铁模块(左右各1个),每个模块由4个电磁铁线圈构成。左右模块相同位置的每2个电磁铁线圈的电磁力简化为一个集中悬浮力。为了用向量式有限元法模拟车-桥系统,对于车辆模型采用多体车辆有限元模型,对于桥梁采用向量式有限元梁单元模拟。在建模前,作出如下合理假设:①只考虑二维的车-桥模型,忽略磁浮车辆的纵向运动(纵向为垂直于重力和轨道中心线的竖直平面方向);②桥梁采用欧拉-伯努利梁来表示,桥梁的截面均匀。将桥梁离散成一组有质量的点,点与点之间用无质量的单元连接。
1.1 车体运动方程
在如图1所示的车-桥模型中,Fij(i=1,…,5,j=1,…,4)为电磁铁产生的悬浮力,mc为车厢质量,mbi(i=1,…,5)为悬浮架质量,zbi为每个悬浮架质心垂向位移,θbi为每个悬浮架转动角度,zc为车厢质心垂向位移,θc为车厢转动角度,lm为2个悬浮架中心距离,lb为悬浮架质心与空气弹簧的距离,ln(n=1,…,10)为车厢质心到每个空气弹簧的距离,cc为空气弹簧阻尼,kc为空气弹簧刚度,Jc为车厢转动惯量,Jbi为悬浮架转动惯量。由上述模型可以得到车体的运动方程,如下所示:

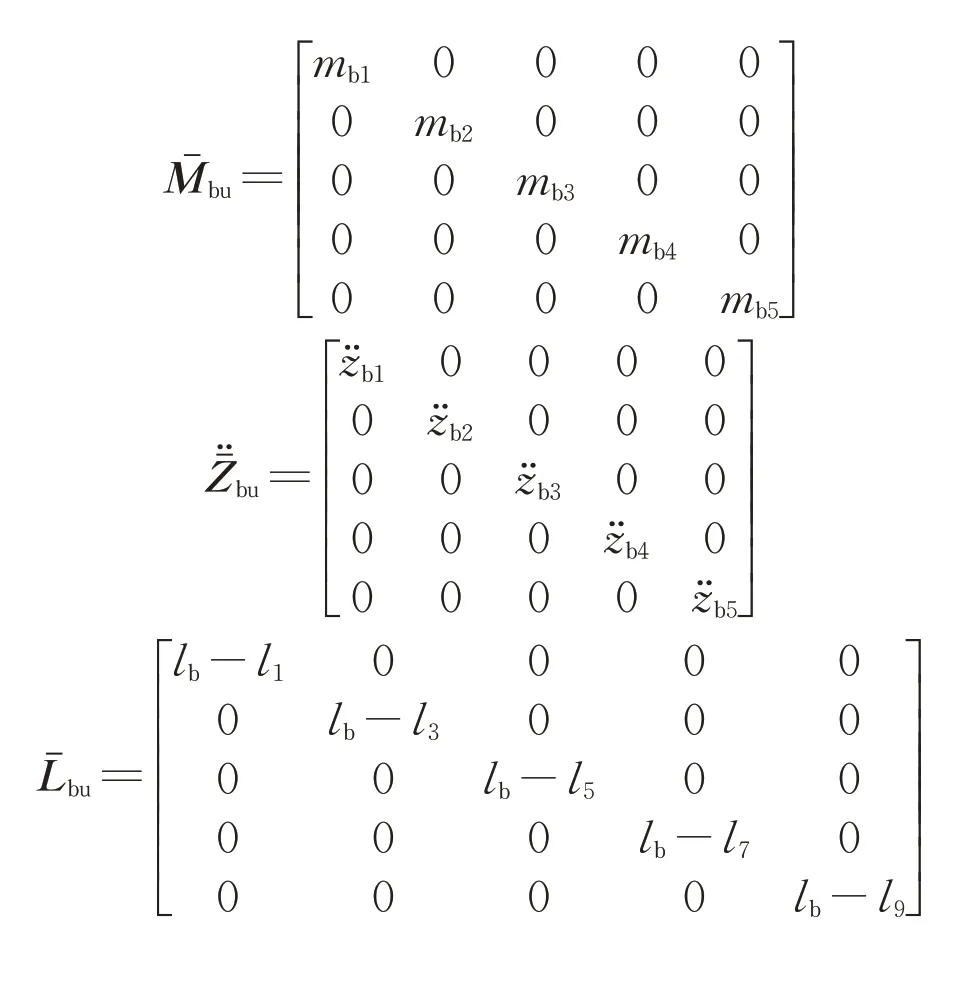
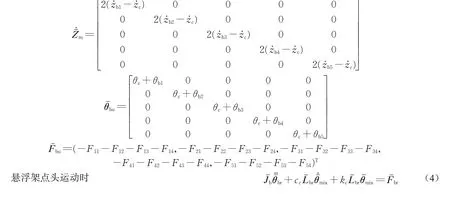
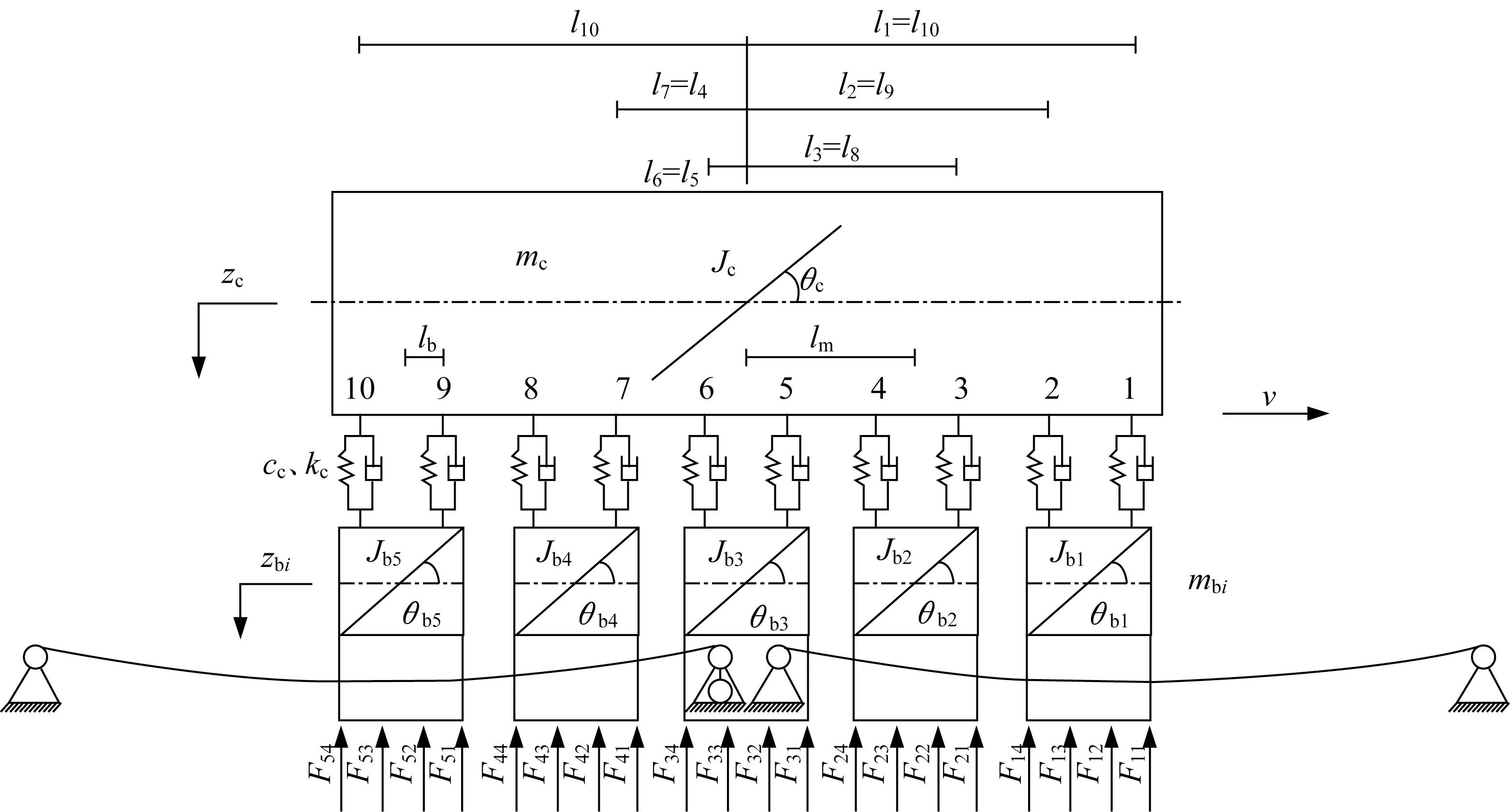
图1 磁浮列车通过多跨简支梁Fig.1 Maglev train passing through multi-span simply supported beam

1.2 可控电磁力模型
对于磁浮列车的悬浮控制,采用双环控制,并取得了成功应用[17]。因为斩波器的成功应用,所以这里只设计电流环。采用经典的比例-微分(PD)控制器,悬浮力F计算式如下所示:
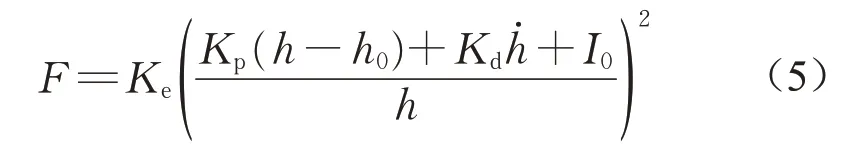
式中:Ke为电磁力常数;Kp为比例项系数;Kd为微分项系数;h为实时悬浮间隙;h0为理想悬浮间隙;I0为平衡电流。
1.3 轨道梁运动方程
对轨道梁作以下假设:
(1)轨道梁看作是无限长的欧拉-伯努利梁。
(2)轨道扣件与桥梁之间采用刚性阻尼连接,如图2所示。

图2 轨-桥计算简图Fig.2 Schematic diagram of rail-bridge calculation
轨道和桥梁模型均采用向量式点值描述,每个点满足牛顿第二定律,而作用在轨道和桥梁上的每个质点的内力可以采用向量式梁单元求得。依据向量式理论,桥梁可采用一组质点进行模拟,相邻质点之间采用向量式梁单元连接,每个质点均满足牛顿第二定律,即:

对于作用在桥梁质点上的内力,可采用向量式梁单元理论中的逆向运动进行求解。向量式有限元法的梁理论是采用点值描述的方法来描述梁受力后其位置的变化,以途径单元将梁的变形简化成每个途径单元内的小变形,这样梁的内力就可采用材料力学的公式来计算;为了得到节点位移中连接单元的纯变形,可将当前时刻梁的构型(1t-2t)做一个虚拟的逆向运动(1d-2d),如图3所示。此逆向运动包括逆向平动位移(-u1)和逆向转动位移-θ。通过梁的虚拟逆向运动,将刚体运动从全位移中分离,以便得到梁的纯变形,即
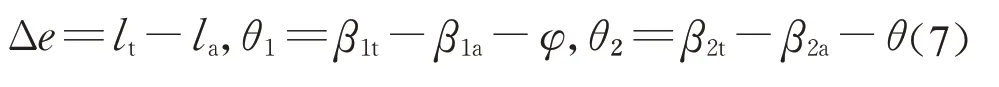

图3 梁单元的逆向运动Fig.3 Reverse motion of beam element
式中:Δe、θ1、θ2分别为轴向纯变形、梁单元节点1和2的纯转动位移;lt和la分别为梁单元的当前时刻(1t-2t)和初始时刻(1a-2a)的单元长度;(β1t,β2t)和(β1a,β2a)分别为节点1和2在当前时刻和初始时刻的转动位移。
在得到梁单元的节点变形后,可采用一组内插函数来计算梁单元上任一点的变形,此插值函数即变形函数。在求得梁单元上每一点的变形后,根据节点内力平衡和节点变形所产生的虚功与梁单元的变形虚功相等的条件,即可求得梁单元的内力。
轨道梁上列车范围内的外力P仅包括轨道与悬浮架之间的悬浮力,即:

式中:F悬为悬浮力。可以利用中心差分法求解车辆和桥梁的微分方程[18-19],表达式如下所示:

式中:a0和a1为阻尼因子;C1=a0h+2和C2=a0h-2分别为与阻尼因子a0有关的阻尼系数;Xα,-1、Xα,0、Xα,n、Xα,n-1和Xα,n+1分别是-1时刻、初始时刻、n时刻、(n-1)时刻和(n+1)时刻的位移矩阵;Fα,0,ext和Fα,n,ext分别是初始时刻和n时刻的外力矩阵;Fα,0,int、Fα,n-1,int和Fα,n,int分别是初始时刻、(n-1)时刻和n时刻的内力矩阵。
2 数值仿真与分析
根据所提出的磁浮列车磁力耦合模型,通过数值仿真来研究该方法的有效性和相关规律。工况为一节磁浮列车分别以60 km·h-1、80 km·h-1和100 km·h-1的速度通过五跨的简支轨道梁。每跨轨道梁之间有简支梁跨端结构缝。磁浮系统相关仿真参数的取值如表1和表2所示。

表1 欧拉-伯努利梁参数Tab.1 Parameters of Euler-Bernolli beam
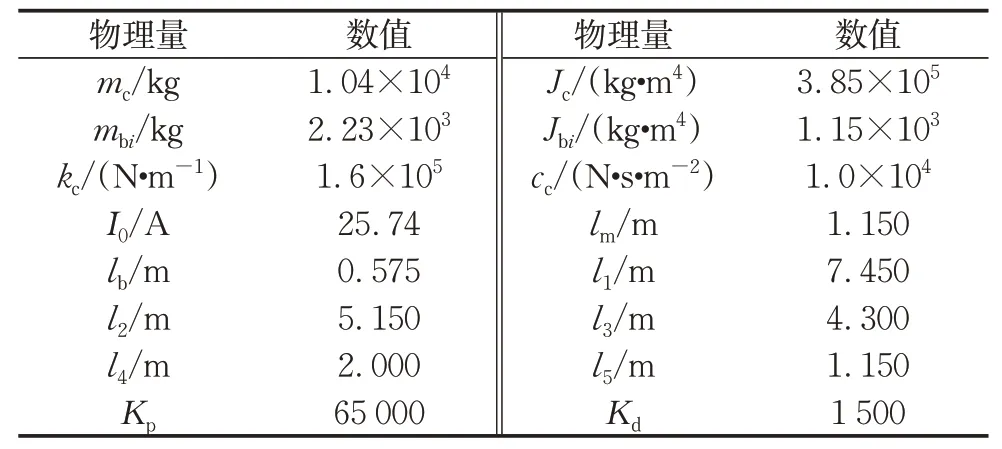
表2 磁浮车辆参数Tab.2 Parameters of maglev vehicle
对60、80、100 km·h-1车速下的磁浮列车动态通过轨道梁的过程进行仿真,梁的跨中垂向位移、梁端转角、梁的中点垂向加速度、车厢垂向加速度、悬浮间隙偏差和电磁力的仿真结果如图4~9所示。
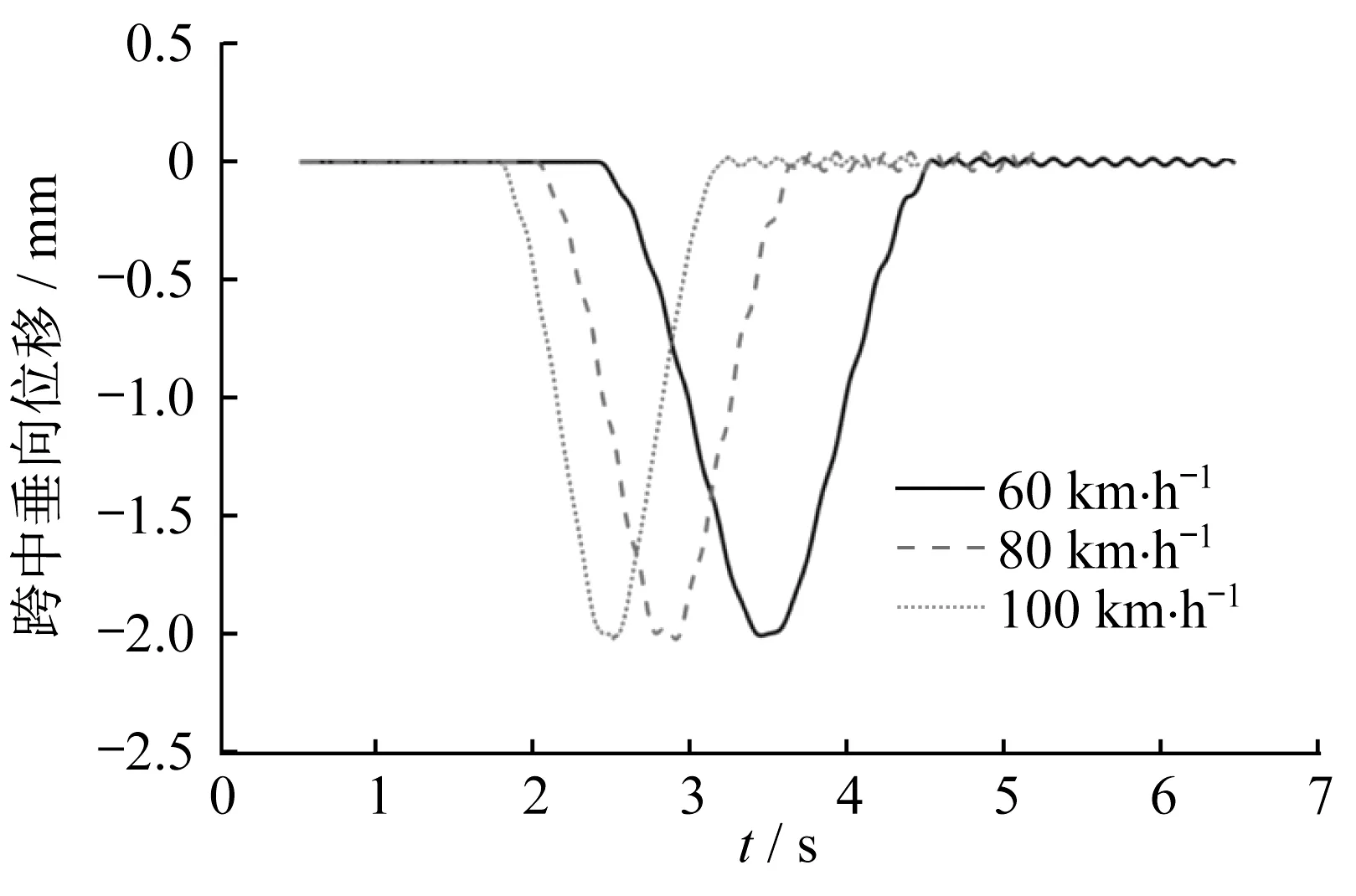
图4 第3根轨道梁的跨中垂向位移Fig.4 Mid-span vertical displacement of the third track beam
从图4~9可以看出,60、80、100 km·h-1车速下,梁的跨中垂向位移分别为2.012、2.014、2.015 mm,而梁端转角分别为0.268 4‰、0.269 4‰和0.274 1‰。图8、9的周期波动是由车辆通过多跨简支梁时产生的,尖峰跳跃是由梁端边界条件产生的。由图4~9可以看出,在低速下轨道梁跨中垂向位移、梁端转角和车厢垂向加速度随速度变化的趋势并不明显,而轨道梁中点垂向加速度、悬浮间隙偏差以及电磁力的振动响应有随速度增大而增加的趋势。
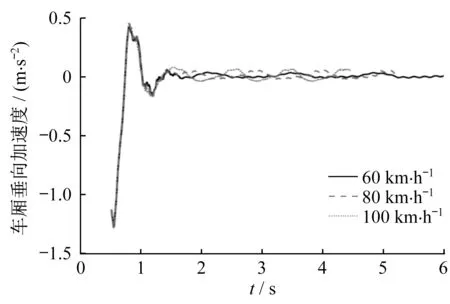
图7 车厢垂向加速度Fig.7 Vertical acceleration of the carriage

图8 悬浮间隙变化Fig.8 Change of airgap
3 试验验证
在同济大学国家磁浮交通工程技术研究中心的上海临港磁浮试验基地进行相关试验,对模型有效性进行初步验证。如图10a所示,上海临港中低速磁浮试验列车为五悬浮架结构[20]。每个悬浮架系统主要由悬浮架、空簧、悬浮电磁铁和悬浮控制器组成。控制算法在悬浮控制器内编程实现,可由上位机实时采集悬浮间隙和悬浮电流,在车厢里可以布置加速度传感器。如图10b所示,在磁浮轨道梁的中点位置布置传感器(压电式加速度传感器、激光位移传感器、拉线式位移传感器、光纤光栅应变传感器),采样频率为5 000 Hz。磁浮列车分别以20、40、60 km·h-1的速度通过高架轨道梁,并通过电压式数据采集仪以及光纤光栅数据解调仪采集相关试验数据。
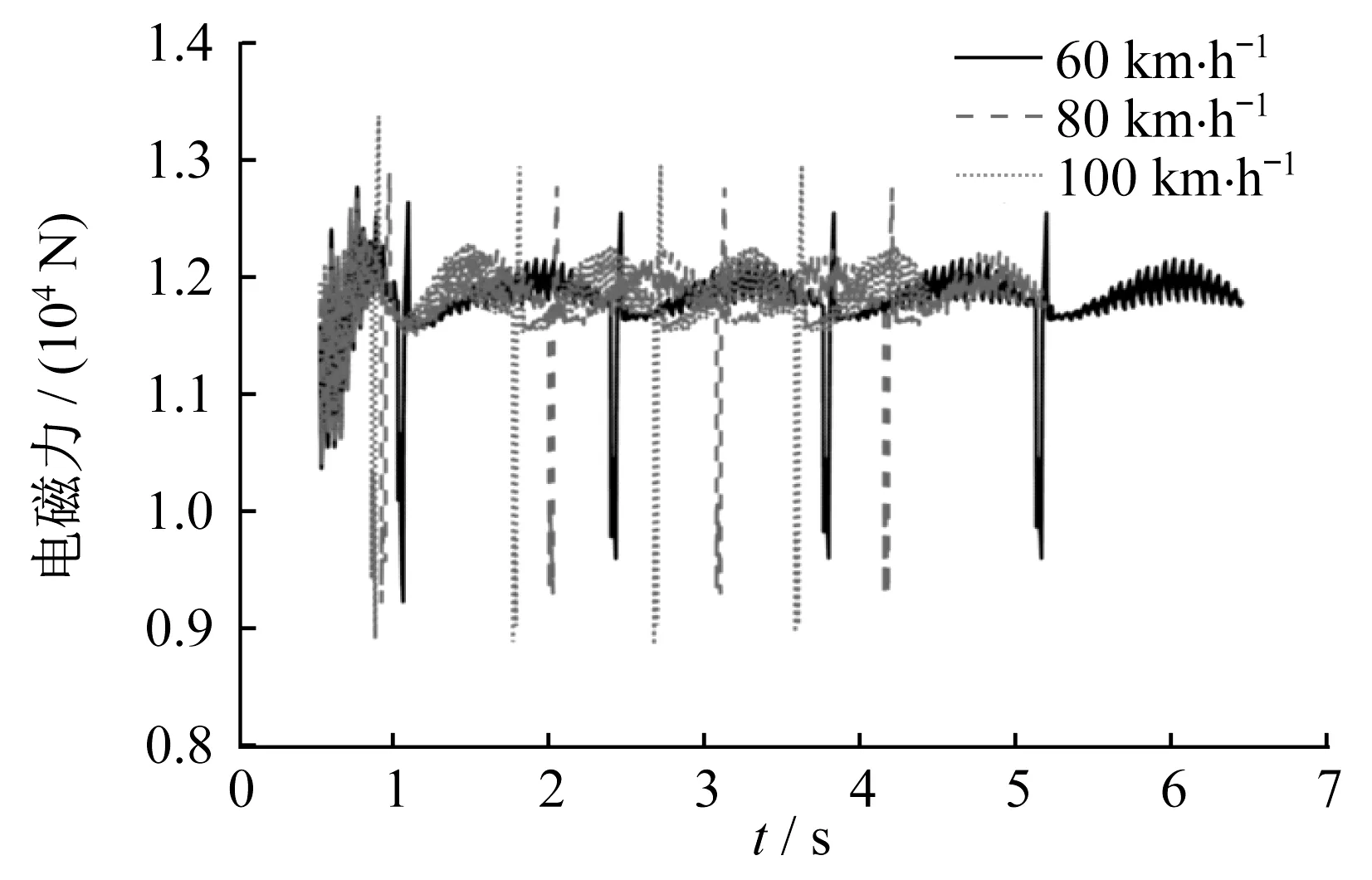
图9 电磁力变化Fig.9 Change of electromagnetic force

图10 试验现场布置Fig.10 Test on site
选取工况为:磁浮列车以60 km·h-1的速度通过轨道梁时的实测数据作对比分析。轨道梁跨中垂向位移实测值和仿真值的对比如图11所示。
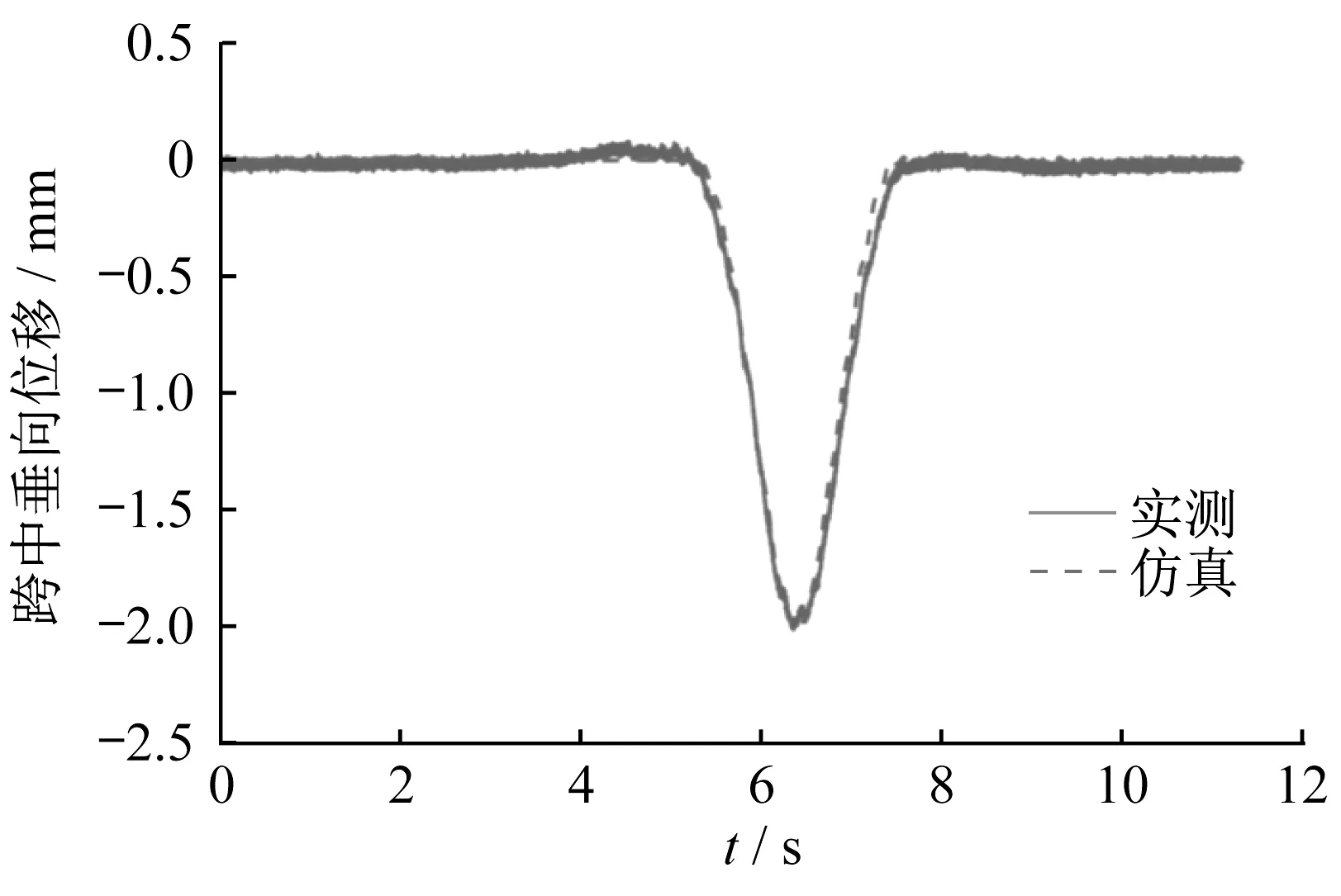
图11 跨中垂向位移的实测值和仿真值对比Fig.11 Comparison of mid-span displacement between measured data and simulation data
实测的最大跨中位移为2.013 mm,仿真的最大跨中位移为2.011 mm。实测数据和仿真数据的曲线重合度较高。平均电流、悬浮间隙和轨道梁振动一阶频率如表3所示。通过数据对比,初步验证了所提出的向量式有限元磁浮列车磁力耦合系统建模方法的有效性。
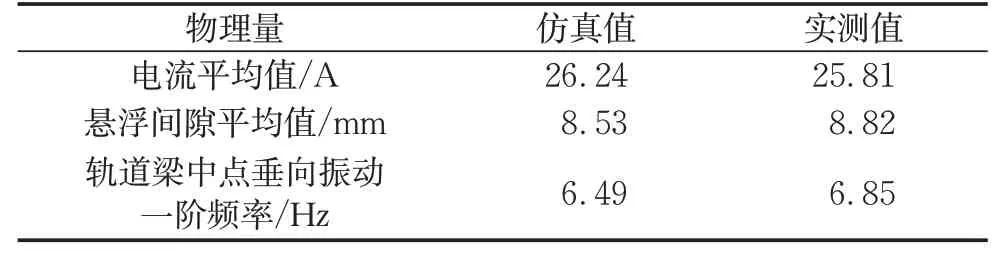
表3 各物理量实测数据和仿真数据对比(60 km·h-1)Tab.3 Comparison of various physical quantities between measured data and simulation data(60 km·h-1)
4 结语
提出了一种基于向量式有限元法的磁力耦合计算模型。分别对60、80、100 km·h-1车速下的磁浮列车动态通过轨道梁的过程进行仿真,获得了梁的跨中垂向位移、梁端转角、轨道梁中点垂向加速度、车厢垂向加速度、悬浮间隙偏差和电磁力的仿真结果。可以看出,轨道梁中点垂向加速度、悬浮间隙偏差以及电磁力对速度的敏感性高于轨道梁跨中垂向位移、梁端转角和车厢垂向加速度。因此,在控制器设计时可考虑引入轨道垂向加速度作为状态反馈,为中低速磁浮的提速设计新的控制算法。最后,在同济大学国家磁浮交通工程技术研究中心的上海临港磁浮试验基地进行整车试验,验证了所提出的基于向量式有限元法的磁浮列车磁力耦合模型的有效性。

