中低速磁浮车辆与U型梁耦合振动响应
梁 潇,向湘林,彭也也,赵春发
(1.湖南磁浮技术研究中心有限公司,湖南长沙410021;2.西南交通大学牵引动力国家重点实验室,四川成都610031)
国内外中低速磁浮交通中大量采用了高架线路,磁浮轨道梁多以混凝土箱梁为主,尚未见U型磁浮轨道梁的应用研究。U型梁较箱梁具有许多优点,如建筑结构高度低、景观适应性好、线路维护及旅客紧急疏散方便等,近年来在我国城市轨道交通中得到较多应用,如上海地铁8号线、南京地铁2号线、重庆轨道交通1号线、青岛地铁13号线、深圳地铁6号线等,目前我国在建的凤凰磁浮旅游线将在国际上首次使用U型磁浮轨道梁。然而,U型梁的截面利用率低,抗扭刚度小,在列车荷载作用下U型梁结构存在剪力滞效应,底板同时承受扭转、剪切和双向弯曲作用,故U型梁的振动和应力应变分布较传统箱梁复杂;进一步考虑到主动控制的悬浮力明显区别于轮轨接触力,这使得磁浮车辆与U型梁的动力相互作用机制及规律与轮轨系统有较大差别。因此,很有必要开展磁浮车辆与U型梁耦合振动的仿真分析,从而为U型磁浮轨道梁的工程设计提供理论指导。
常导磁浮列车技术研究起始于20世纪70年代,国内外随之开展了磁浮车-桥耦合动力学研究[1-3]。早期研究中将磁浮车辆和桥梁进行相当大的简化处理,基本不考虑主动悬浮控制系统和桥梁细致结构,主要为系统方案设计提供依据;后期日本、中国和韩国为开发常导磁浮交通实用化技术,更细致、更全面地开展了磁浮车-桥耦合动力学研究。赵春发等[4-5]、时瑾等[6-7]结合上海高速磁浮示范线工程,建立高速磁浮车辆-轨道梁耦合动力学模型,考虑主动悬浮控制和轨道不平顺激扰,分析了磁浮车辆和轨道梁动力作用机制及主要参数的影响规律。Yang等[8]将轨道梁简化为伯努利-欧拉梁,考虑地基-土壤的相互作用,分析了高速磁浮车辆运行于高架桥上的动力学性能。翟婉明等[2]和赵春发等[3]分析了电磁悬浮的力学特性,研究了中低速及高速磁浮列车通过高架桥梁和曲线线路时的动力学性能。Ju等[9]以韩国仁川机场磁浮线为对象,建立了磁浮车辆动力学模型和包含桥墩、桩基和土壤的桥梁有限元模型,开展了磁浮列车-桥梁-桩基-土壤动力相互作用分析。Min等[10]建立了包含5个状态反馈控制的中低速磁浮车辆动力学模型,将轨道梁考虑为垂向、横向和扭转方向上相互独立的伯努利-欧拉梁模型,研究了磁浮车-桥耦合共振条件和轨道不平顺对车-桥耦合振动响应的影响。李小珍等[11]、耿杰等[12]和王党雄等[13]结合长沙磁浮快线工程,开展了磁浮列车-桥梁耦合振动的数值模拟和试验研究,分析了F型轨对系统动力学响应的影响。Zhang等[14]建立了十自由度高速磁浮车辆垂向动力学模型,以及包含功能件、弹性支座和简支变连续连接件的轨道梁有限元模型,基于实测轨道梁固有频率校正了轨道梁模型参数,采用了增量迭代法求解车-桥耦合振动响应,并将仿真结果与上海高速磁浮运营线和试验线的实测结果进行了对比分析,验证了所提出的磁浮车-桥耦合动力学建模与求解方法的有效性。Xu等[15]提出了一种高速磁浮车辆与曲梁动力相互作用模型及其数值分析方法,研究了曲线半径、缓和曲线长度、超高角对磁浮车辆曲线通过性能的影响。为了更精确地模拟磁浮车-桥耦合振动响应,李倩等[16]开发了基于Simpack和Ansys软件的磁浮交通系统分布式协同仿真平台,在磁浮车辆系统多学科建模以及轨道和桥梁结构精细化有限元建模的基础上,实现了磁浮车-轨-桥系统动力学耦合计算;利用该平台,任晓博等[17]、张宇生[18]分别开展了中低速磁浮车-轨-桥系统和车-岔系统耦合振动分析,数值模拟再现了低速运行条件下磁浮车-轨耦合振动剧烈的现象。综上,学者们提出了繁简不一的磁浮车-桥耦合动力学模型,建立了更细致的悬浮架、轨道及桥梁结构的动力学模型,准确模拟“磁-轨”动力相互作用以支撑磁浮交通系统精准化设计与评估是当前的主要趋势。
近年来我国在轮轨交通U型梁动力性能方面也开展了较多的研究,这些工作可为磁浮交通U型梁的研究与开发提供参考。吴亮秦等[19]计算了不同编组列车和行车速度条件下U型梁的位移动力系数、道床板局部应力动力系数和列车过桥平稳性等,结果表明梁端道床板与腹板相交处横向负弯矩变化幅值较大,易发生疲劳损伤而顶面开裂,建议采用总体和局部应力动力系数进行桥梁结构承载力设计。王彬力等[20-21]结合重庆市轨道交通1号线工程,开展了U型梁动力性能的数值分析与试验研究,对U型梁引起的环境振动进行了评价。汪振国等[22]采用Simpack软件建立了地铁车辆动力学模型,采用了模态叠加法求解U型梁和箱梁振动响应,比较了2类轨道梁的动力学响应,并指出U型梁的横向振动不容忽视,尤其应注意U型梁翼缘与腹板的振动。张景峰等[23]采用了显式动力有限元软件建立列车-U型梁碰撞模型,对碰撞全过程进行了仿真分析,将计算结果与相关规范报告进行了对比,最后分析了U型梁的碰撞损伤模式。李奇等[24]提出一种车-轨-桥高频耦合振动分析的功率流方法及模型,对比不同轨-桥模型对U型梁和箱梁振动功率的影响,并指出U型梁桥面板的剪切效应对桥梁振动功率计算结果的影响很大,采用Mindlin板模型可获得良好的计算精度与效率。罗锟等[25]针对城市轨道交通中U型梁引起的振动噪声问题,建立了U型梁-调谐质量阻尼器(TMD)耦合振动模型,分析了移动集中力作用下TMD对U型梁低频振动的实际控制效果。以上研究表明,U型梁和箱梁的动力性能有较大的差别,其中U型梁翼缘和腹板的局部振动较大,并存在结构振动噪声问题,这意味着对U型梁的动力学分析有必要建立更精细的模型。
针对凤凰磁浮旅游线的简支U型轨道梁,利用Simpack软件建立考虑比例-积分-微分(PID)悬浮控制的2节编组磁浮列车动力学模型,采用Ansys软件建立轨道结构和U型梁梁体的有限元模型,并开展轨道及梁体结构的模态分析。利用自主开发的磁浮车-桥系统动力学耦合计算器,计算20~100 km·h-1行车速度范围内磁浮车-桥系统的动力学响应,重点分析100 km·h-1速度工况下磁浮车辆、轨道和U型梁梁体的动力学响应特征,以及车-轨-桥系统动力学响应随行车速度的变化规律。依据现有轮轨铁路和磁浮交通的相关技术规范,综合评估中低速磁浮车辆与U型梁的动力性能,以期为U型磁浮轨道梁的设计与工程应用提供理论指导。
1 中低速磁浮车辆系统动力学模型
1.1 车辆模型
以凤凰项目中低速磁浮列车为参考对象建立车辆动力学模型,如图1所示。磁浮车辆由车体、二系空气弹簧悬挂系统、悬浮架、悬浮电磁铁、迫导向机构、牵引与制动装置以及各种辅助设备组成。每车配备5个悬浮架,悬浮架主要由左右2个悬浮模块和2对防侧滚梁组成。悬浮模块是车辆悬浮、导向和牵引的基本单元,由托臂、箱梁、悬浮电磁铁、直线电机定子等部件构成。安装于悬浮模块端部的防侧滚梁约束模块的侧滚运动,允许左右模块有其他方向上的相对运动。空气弹簧位于悬浮模块的两端,每个悬浮架装配4个空气弹簧,空气弹簧上端与车厢底部的支承台连接,其中左右侧第2个和第5个支承台与车厢底部固结,其他位置支承台与车厢之间安装直线轴承,允许两者之间横向滑动。每节车辆的第1个和第2个悬浮架、第4个和第5个悬浮架之间安装迫导向机构,该机构由前后2个T型臂、2根钢缆及横向拉杆组成,形成一个平行四边形连杆机构(见图2),能够迫使前后悬浮模块跟随曲线轨道运行。

图1 凤凰项目中低速磁浮列车示意图Fig.1 Schematic diagram of medium-low speed maglev train in Fenghuang project
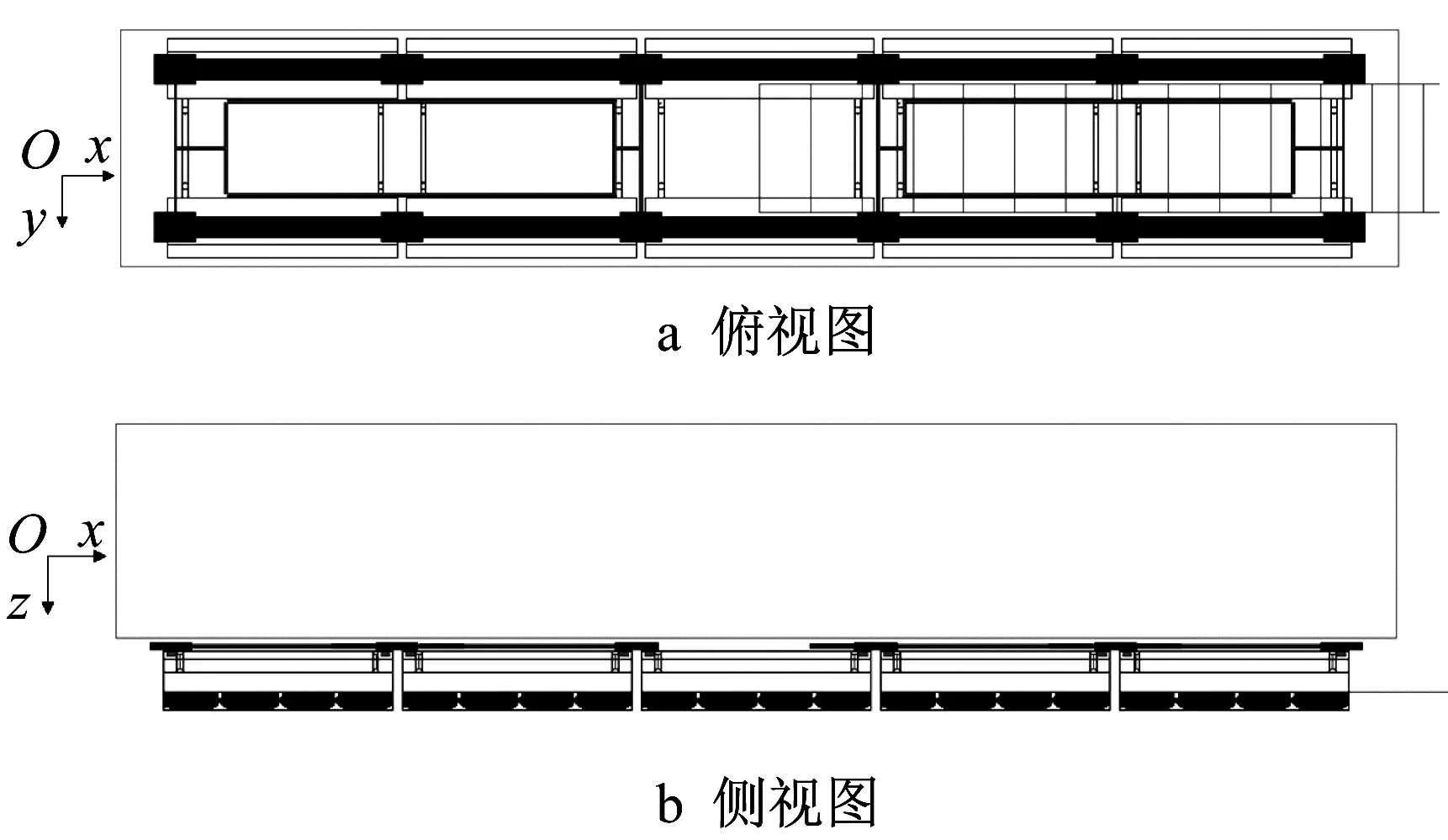
图2 中低速磁浮车辆动力学模型Fig.2 Dynamic model of medium-low speed maglev vehicle
在明晰中低速磁浮车辆各部件运动关系的基础上,将车体、悬浮模块、防侧滚梁等部件视为刚性体,二系空气弹簧悬挂系统模拟为线性弹簧阻尼器,车体和悬浮模块均考虑6个运动自由度。防侧滚梁与悬浮模块铰接,仅考虑其绕z轴的转动自由度;左、右两片防侧滚梁之间通过2个吊杆连接,只考虑吊杆绕x轴的转动自由度。将迫导向机构T形臂、横向拉杆和钢索均考虑为杆单元,相互之间通过铰单元相连,仅考虑绕z轴的转动自由度。牵引拉杆两端分别与支承台和牵引支座铰接,考虑其6个方向上的运动自由度。最终,采用Simpack软件建立了如图2所示的中低速磁浮车辆动力学模型,每节车辆共有181个刚体运动自由度。为了使U型梁能够满跨承受车辆悬浮荷载,进一步建立了2节编组的磁浮列车动力学模型。表1列出了磁浮车辆动力学模型的主要参数。

表1 中低速磁浮车辆动力学模型主要参数Tab.1 Main parameters of dynamic model of medium-low speed maglev vehicle
1.2 主动控制的电磁悬浮模型
中低速常导磁浮车辆利用U型电磁铁与F型导轨之间的电磁吸力提供支承力,导向力来自于U型电磁铁的横向回复力。假定电磁铁的悬浮和导向间隙均匀,不考虑磁泄露和磁饱和,电磁悬浮力Fz和导向力Fy的计算式为
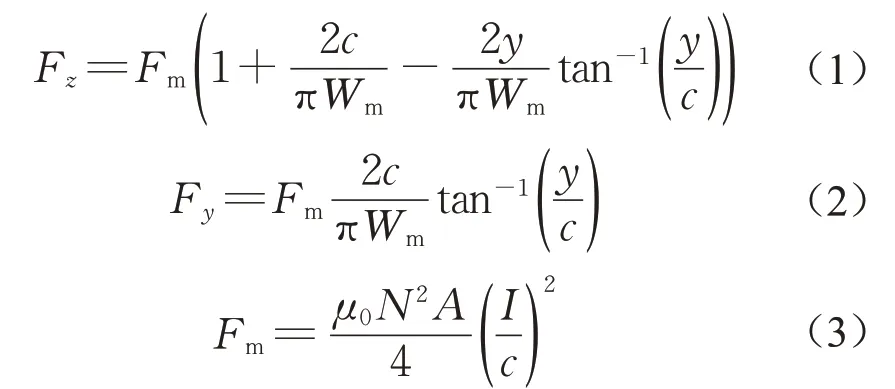
式中:c为悬浮间隙;y为电磁铁与导轨之间的横向偏移量;Wm为有效磁极宽度;A为磁极面积;I为线圈电流;N为线圈匝数;μ0为空气磁导率。
常导磁浮车辆一般采用位置环+电流环的双环控制器实时调节电磁铁电流,从而实现车辆的稳定悬浮。电流环使得线圈电流快速跟踪电压,对电磁悬浮系统动态响应的影响很小,因此磁浮车辆动力学仿真中只需考虑位置环。采用实际工程中使用的PID悬浮控制算法,电磁铁电流的控制律为
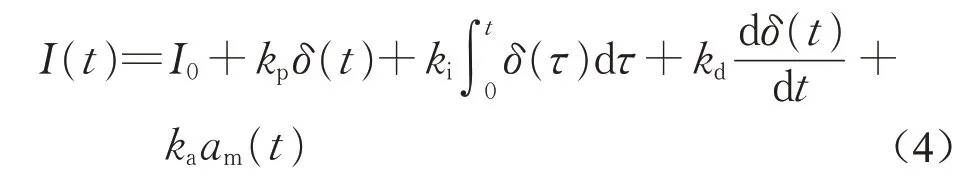
式中:δ(t)为悬浮间隙偏差;kp、ki和kd分别为悬浮间隙偏差的比例系数、积分系数和微分系数;ka为电磁铁加速度反馈系数;am(t)为电磁铁加速度;I0为电磁铁额定电流。将式(4)计算得到的电流值代入式(1)和式(2),就可以得到主动控制的电磁悬浮力和导向力。
采用Matlab/Simulink软件建立电磁悬浮控制系统模型,并生成Simpack软件可调用的MatSim文件,每节磁浮车辆共有20个悬浮控制器。
1.3 磁浮轨道不平顺模型
轨道不平顺是磁浮车-桥耦合振动的主要外部激励,目前国际上尚无成熟的中低速磁浮轨道不平顺谱。张耿等[26]基于唐山中低速磁浮试验线的实测不平顺数据,给出了轨道高低不平顺和轨向不平顺功率谱的拟合公式,并与美国和德国轨道谱进行了比较,结果表明在3~20 m波长范围内磁浮轨道不平顺谱与德国高速低干扰谱较为接近。然而,唐山中低速磁浮轨道不平顺谱的实测样本偏少,最大有效波长仅为20 m,还不能满足磁浮车辆动力学仿真需求,因此本研究中基于德国高速低干扰谱生成磁浮轨道不平顺样本。图3给出了反演得到的轨道高低不平顺空间样本,不平顺波长范围为0.5~50.0 m,不平顺幅值不超过4 mm。
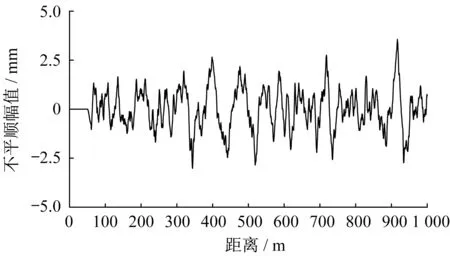
图3 轨道高低不平顺空间样本Fig.3 Spatial sample of vertical track irregularity
2 轨道和U型梁结构有限元模型
2.1 轨道和U型梁建模
凤凰项目中简支U型梁的标准跨度为25 m,梁高为1.7 m,一般部位板厚为26 cm,梁端支座范围内底板局部加厚至40 cm,U型梁跨中截面如图4所示。对于U型梁,主梁采用C55混凝土,在工厂内预制;现场浇筑承轨台,轨道结构与承轨台通过扣件相连。
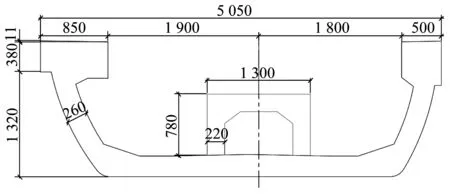
图4 U型梁跨中断面示意图(单位:mm)Fig.4 Schematic diagram of mid-span cross section of U-type girder(unit:mm)
使用Solidworks软件建立轨道和U型梁结构的三维几何模型,然后采用Hypermesh软件进行网格划分,在Ansys软件中选用Shell 181板壳单元,最终建立如图5所示的轨道和U型梁结构有限元模型。F型导轨和H型轨枕间的连接采用cp单元进行模拟,轨枕和承轨台间扣件系统模拟为弹簧单元。图5还标出了下文中轨道和梁体动力学响应的观测点,分别在跨中处左侧腹板中心、底板中心和右侧腹板中心(U2、U4和U5),在右侧F型轨外腿底部设置观测点F6,在轨枕顶面中心处设置观测点H2。表2列出了轨道和U型梁结构的材料参数。
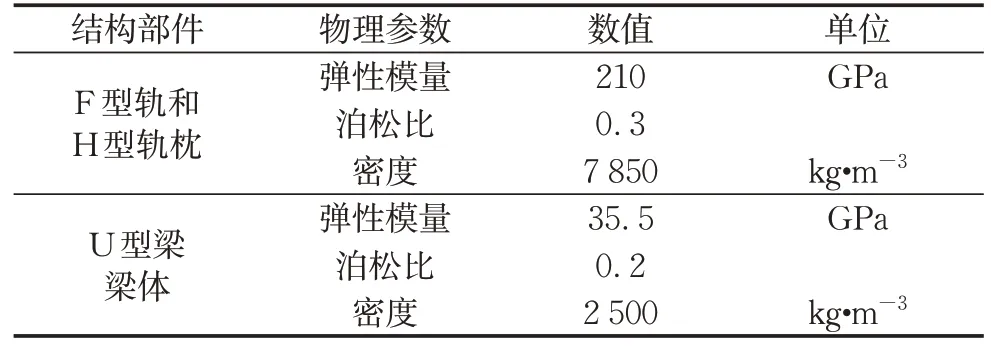
表2 轨道和U型梁结构材料参数Tab.2 Material parameters of track and U-type girder structure
图5仅给出了1跨U型梁有限元模型,下文中在磁浮车-桥耦合动力学仿真计算时,实际建立了3跨U型梁的精细化有限元模型,并在精细化U型梁模型的前、后各建立了2跨梁单元有限元模型,故共有7跨轨道梁参与车-桥耦合动力学仿真计算,从而在第4跨梁上可以获得更为稳定的车-桥耦合动力学响应。
2.2 轨道和U型梁结构模态分析
图6给出了轨道和U型梁结构的前8阶模态振型。第1阶振型为竖弯模态,自振频率为5.57 Hz,满足我国《中低速磁浮交通设计规范》(CJJ/T 262―2017)[27]规定的简支轨道梁竖向频率限值要求(f1≥64/L=2.56 Hz);第2阶振型为横弯模态,频率为6.60 Hz;第3阶振型为二阶竖弯伴随扭转模态,频率为16.43 Hz;由于U型梁为开口槽形梁,第4~8阶模态中包含了明显的腹板扭转和呼吸模态。
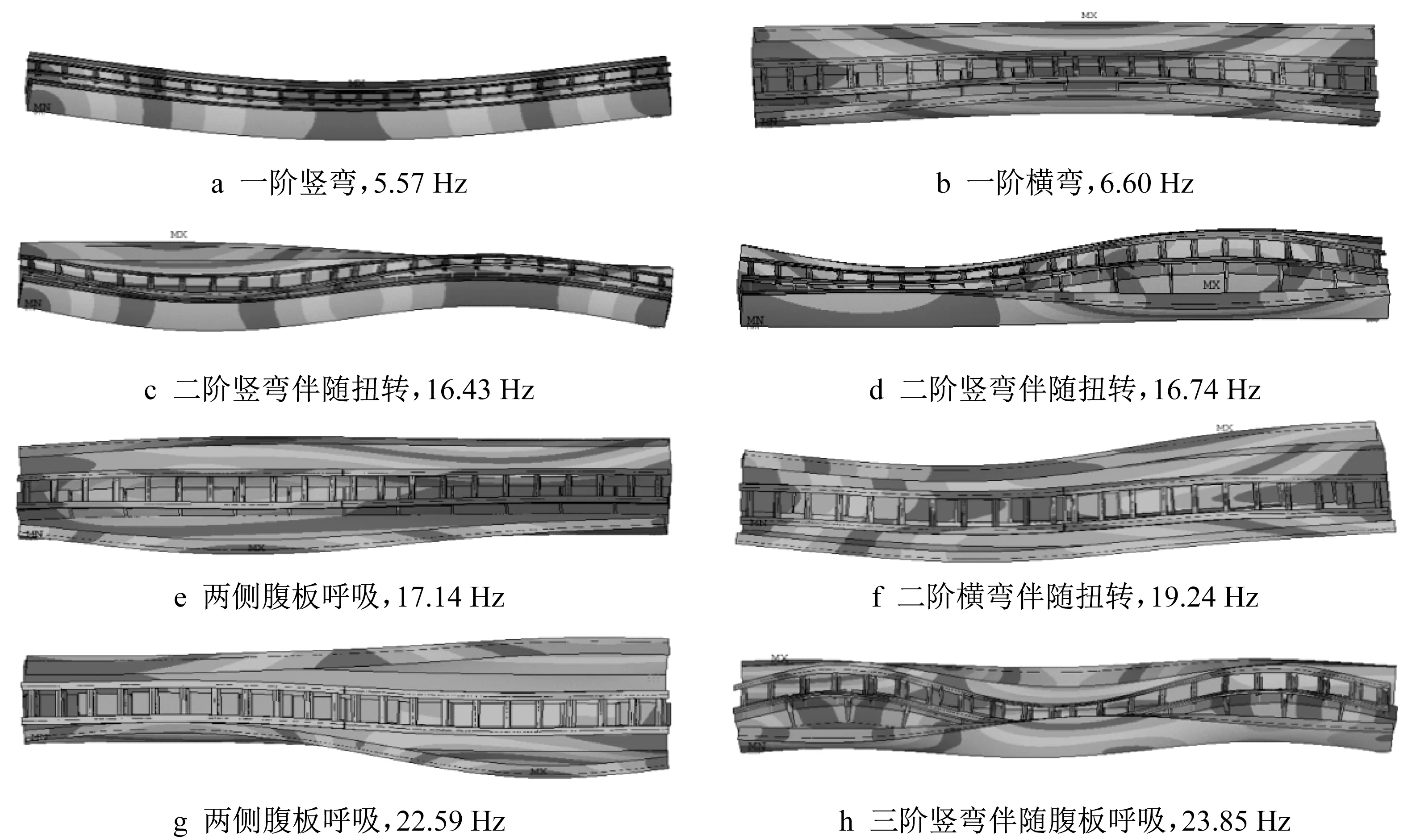
图6 轨道和U型梁结构的模态振型Fig.6 Modal shapes of track and U-type girder structure
图7给出了轨道和U型梁结构的第25阶模态振型,可以发现该振型主要表现为轨排的竖弯模态,模态频率为55.76 Hz。类似的轨排振动模态频率主要分布在40~70 Hz,限于篇幅,不再详细给出。
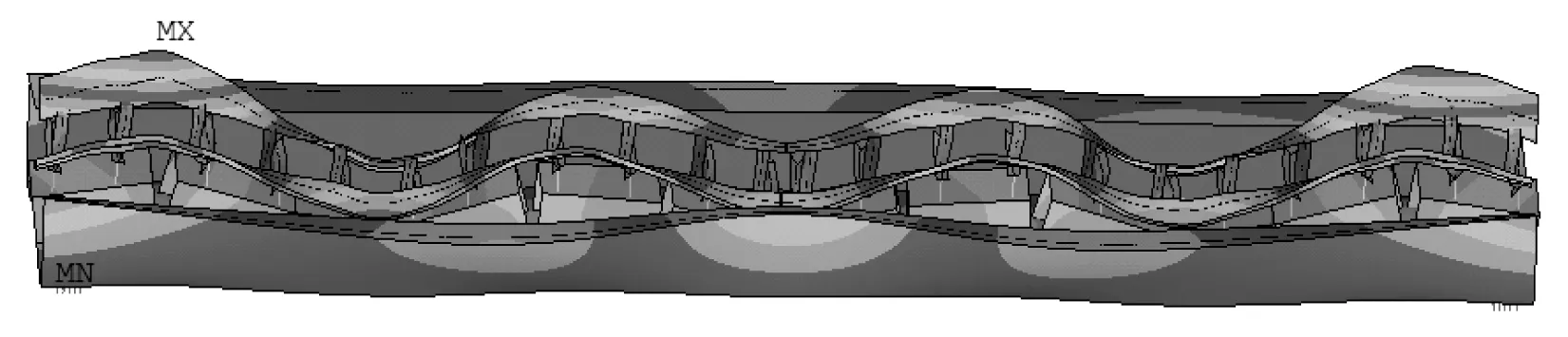
图7 轨道和U型梁结构的第25阶模态振型Fig.7 The 25th-order modal shape of track and Utype girder structure
3 磁浮车-桥耦合振动数值模拟方法
采用西南交通大学赵春发教授课题组开发的磁浮交通系统分布式协同仿真平台[16]实现Simpack磁浮车辆模型与Ansys桥梁有限元模型的step-by-step耦合仿真,分布式协同仿真平台包括2台高性能工作站、Simpack软件平台、Ansys软件平台以及自主开发的接口程序和耦合计算器。Simpack仿真模块和Ansys仿真模块通过接口程序与耦合计算器进行数据交互和耦合计算,耦合器控制分布在不同计算机上任务模块输入输出数据的收发和仿真时序,根据工况中各个任务模块之间的耦合关系和各任务模块的仿真状态,通过通告算法推算出能进行下一步仿真的任务模块,并通过网络通知相应的执行机(Simpack计算器和Ansys计算器)。耦合器与执行机之间的工作流程如图8所示。
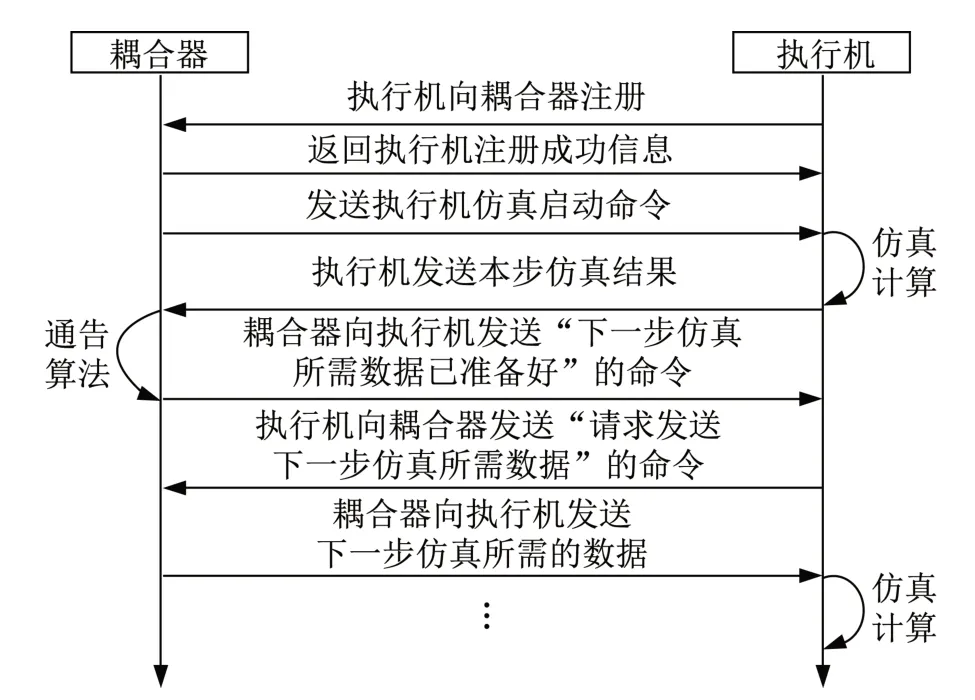
图8 耦合器与执行机的工作流程[16]Fig.8 Working process of coupling calculator andexecuting machines[16]
4 中低速磁浮车辆与U型梁耦合振动响应分析
采用前文建立的2节编组磁浮列车模型和7跨U型梁有限元模型,计算了20~100 km·h-1速度工况下中低速磁浮车-轨-桥系统的动力学响应。首先分析了100 km·h-1速度工况下磁浮车辆、U型梁梁体和轨道结构的动力学响应特征,然后给出了磁浮车辆与U型梁耦合振动响应随行车速度的变化规律。
4.1 速度100 km·h-1时车-轨-桥系统动力学响应
4.1.1 轨道和梁体振动响应
图9为行车速度100 km·h-1工况下第4跨U型梁跨中处梁体、F型轨和轨枕观测点的竖向位移。从图9可以看出,梁体、F型轨和轨枕的竖向位移波形相似,动位移全幅值均约0.70 mm,但最大绝对幅值略有差别。梁体底板U4点处的最大竖向位移为3.00 mm,对应的竖向挠跨比约为1/8 333,远小于我国《中低速磁浮交通设计规范》(CJJ/T 262―2017)[27]规定的简支轨道梁竖向挠跨比限值1/3 800。F型轨外腿F6点和轨枕顶面H2点处的最大竖向位移分别为3.81 mm和3.21 mm。右腹板U5点和梁体底板处的竖向位移接近,大于左腹板U2点约0.30 mm,原因是轨道中心线与底板中心线存在118 mm的偏差。
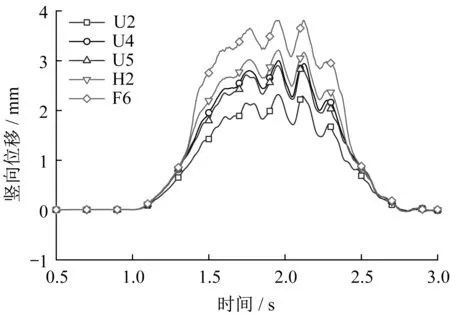
图9 100 km·h-1速度工况下跨中处梁体及轨排结构竖向位移Fig.9 Vertical displacement of girder and track at mid-span with train speed of 100 km·h-1
图10为U型梁底板U4点和F型轨外腿F6点处的竖向加速度响应时程。从图10可以看出,F型轨外腿的竖向加速度响应明显大于U型梁底板,两者的加速度最大值分别为7.69 m·s-2和1.03 m·s-2。图11为F型轨外腿和U型梁底板竖向加速度响应的频谱。频谱分析表明:U型梁底板竖向加速度响应的优势频率集中在30 Hz以内,主要包括5.59 Hz、16.49 Hz和23.48 Hz,分别接近于轨道和U型梁结构的第1~3阶竖弯模态频率;F型轨竖向加速度响应的优势频率分布在40~70 Hz内,其中55.44 Hz的振动表现最显著,该频率与轨道和U型梁结构的第25阶模态频率接近,并且在U型梁底板竖向加速度响应的频谱图中有所表现。

图10 U型梁底板和F型轨外腿的竖向加速度响应(速度为100 km·h-1)Fig.10 Vertical acceleration response at the bottom slab of U-type girder and the outside leg of F-rail(velocity is 100 km·h-1)
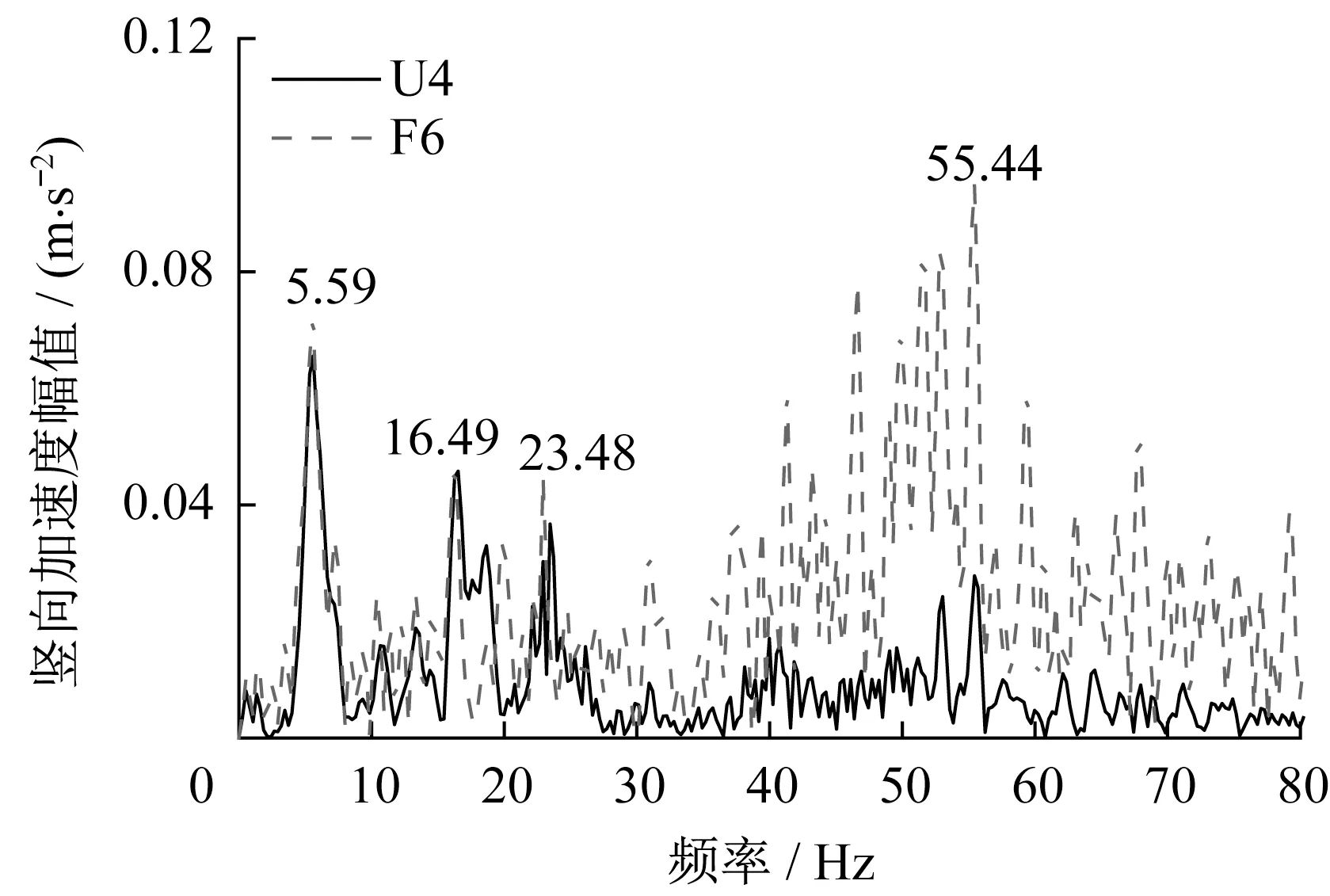
图11 U型梁底板和F型轨外腿的竖向加速度响应频谱(速度为100 km·h-1)Fig.11 Spectrum of vertical acceleration response at the bottom slab of U-type girder and the outside leg of F-rail(velocity is 100 km·h-1)
4.1.2 车辆系统动力学响应
图12分别为行车速度100 km·h-1工况下车体质心竖向加速度和车辆左侧第1个悬浮模块竖向加速度响应时程。结果表明:车体质心竖向加速度最大值不超过0.13 m·s-2,优势主频与车辆二系悬挂频率(约1.0 Hz)接近,磁浮车辆运行非常平稳;悬浮模块的竖向加速度明显大于车体质心加速度,最大值为3.80 m·s-2。从图13可以发现,悬浮模块加速度响应的主频为1.26 Hz,这与车辆二系悬挂频率和车辆通过桥梁的频率(1.11 Hz)接近。悬浮模块加速度响应频谱还包含了10~20 Hz的优势频率成分,与轨道和U型梁结构的第2、第3阶竖弯模态频率以及电磁悬浮系统特征频率相关。
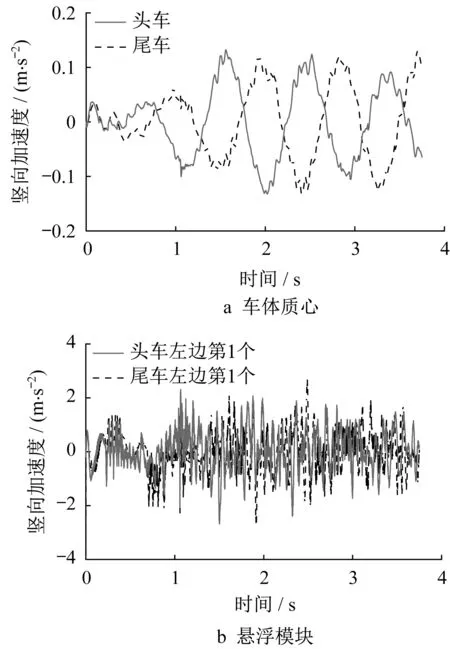
图12 车体质心和悬浮模块竖向加速度响应(速度为100 km·h-1)Fig.12 Vertical acceleration response of carbody centroid and levitation module(velocity is 100 km·h-1)
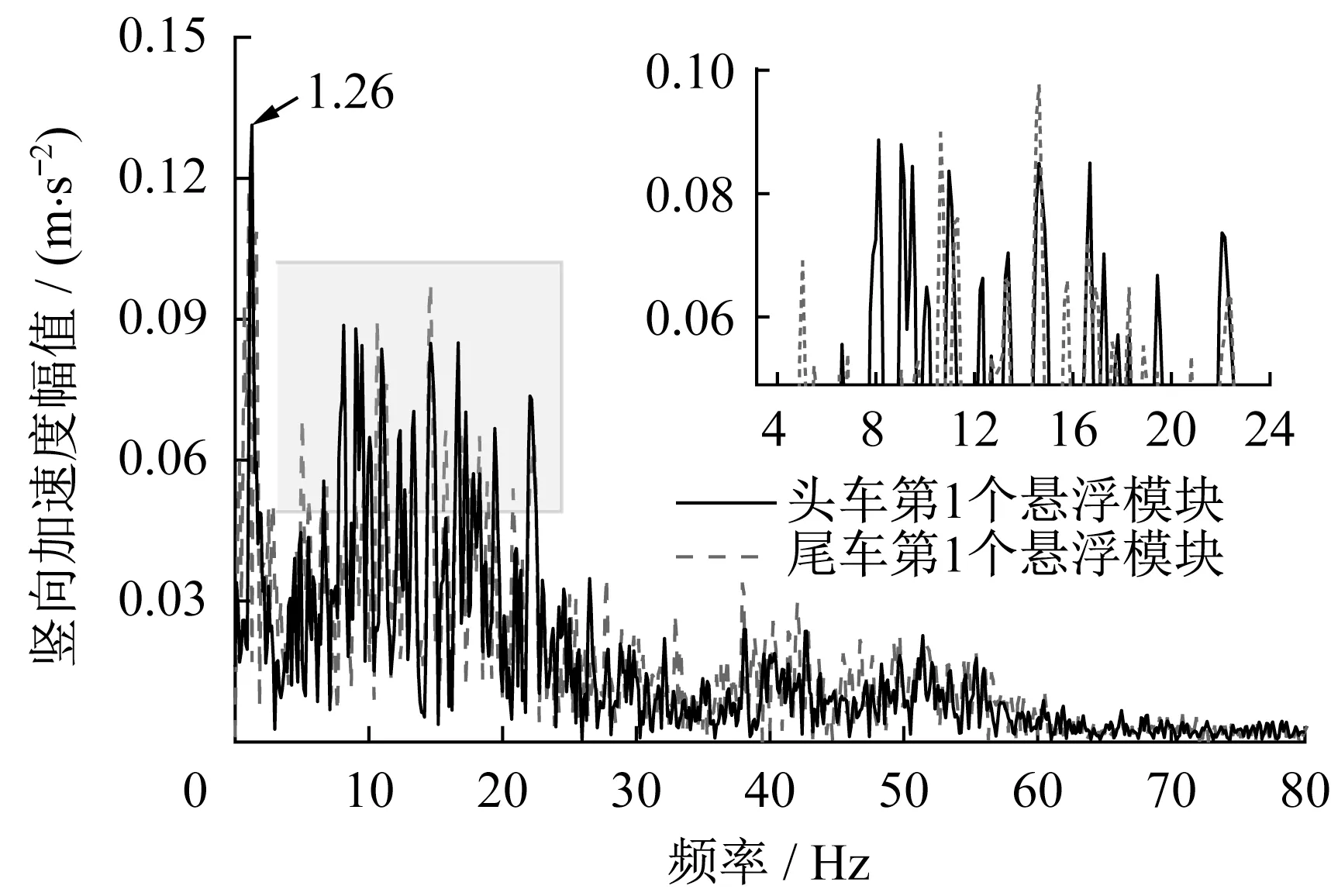
图13 悬浮模块竖向加速度响应频谱(速度为100 km·h-1)Fig.13 Spectrum of vertical acceleration response of levitation module(velocity is 100 km·h-1)
图14为行车速度100 km·h-1工况下车辆左边第1个电磁铁前端的悬浮间隙变化。从图14可以看出,电磁铁悬浮间隙在7.2~8.4 mm之间波动,相对于额定悬浮间隙的最大偏差为0.8 mm,小于允许的悬浮间隙波动限值4.0 mm,说明该速度工况下磁/轨发生碰撞的风险不大。
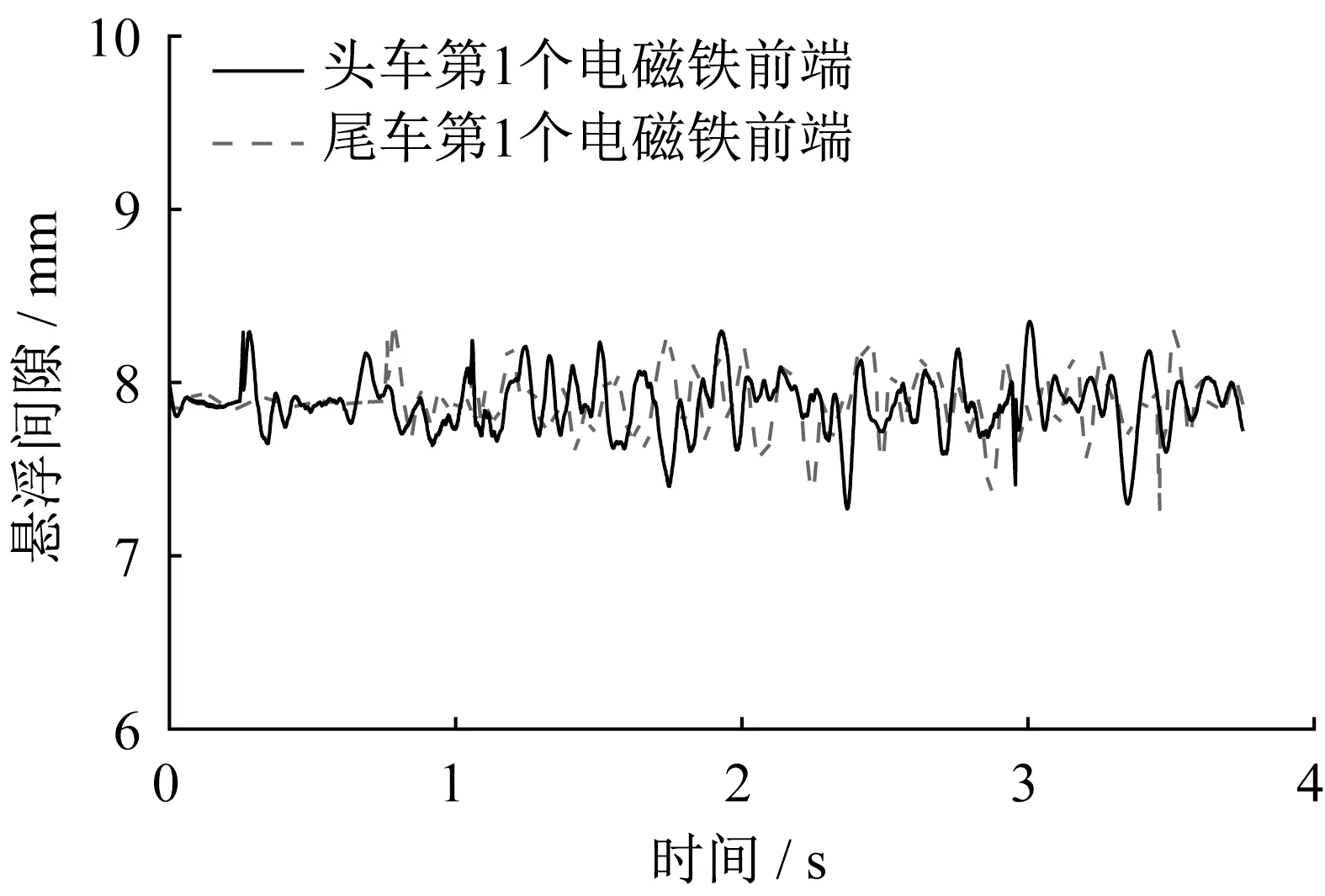
图14 电磁铁悬浮间隙变化(速度为100 km·h-1)Fig.14 Levitation gap variation of electromagnets(velocity is 100 km·h-1)
4.2 车-轨-桥系统动力响应随行车速度的变化
图15为跨中处U型梁底板、F型轨和轨枕的竖向位移幅值随行车速度的变化。可以发现,在20~100 km·h-1速度下,梁体和轨道的竖向位移幅值总体上随速度提高略微增大,均在速度为100 km·h-1时达到最大值,梁体底板的最大竖向位移幅值约为3.0 mm。
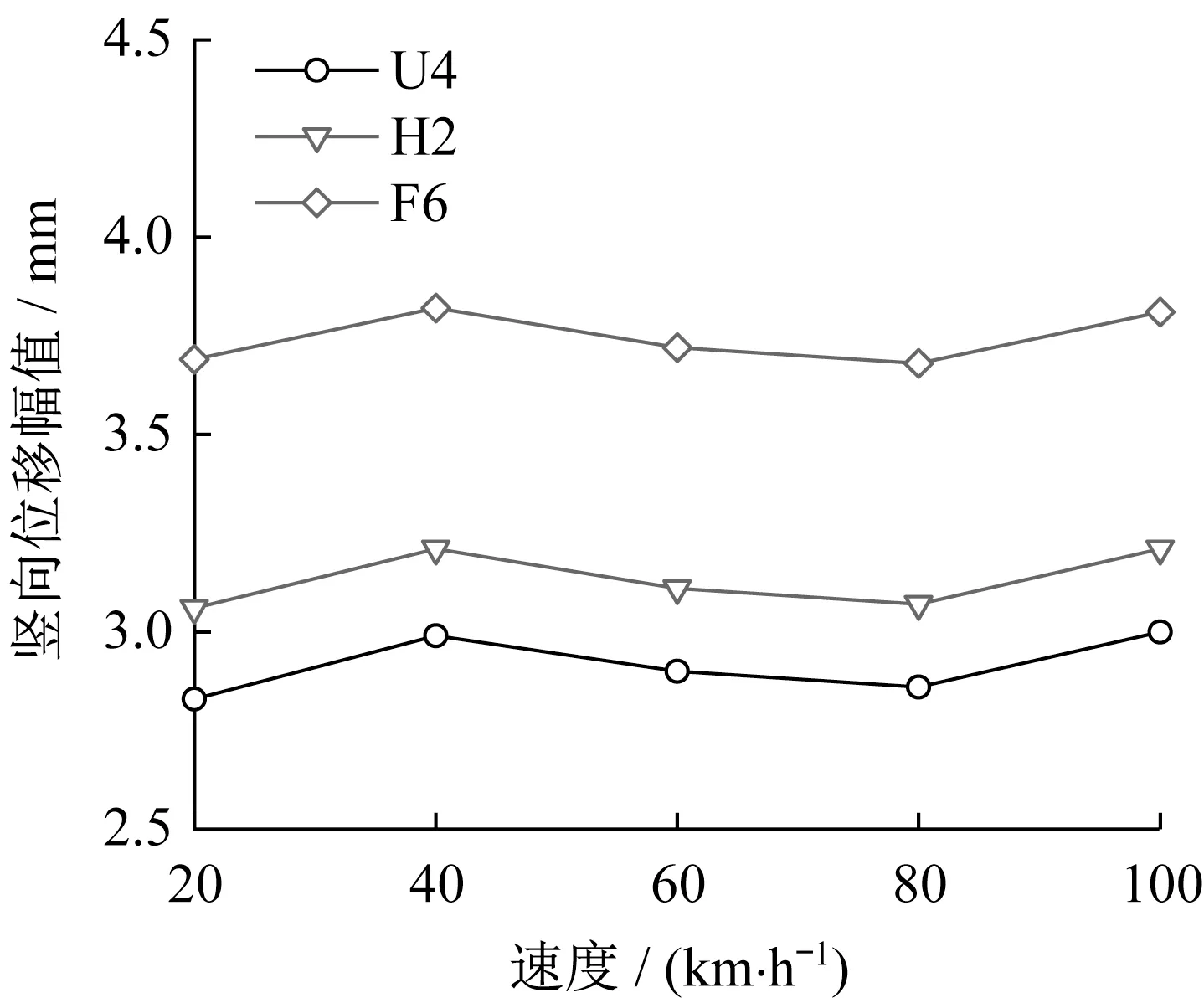
图15 跨中处U型梁和轨道竖向位移幅值与行车速度的关系Fig.15 Relationship between vertical displacement amplitude of U-type girder and track at the mid-span and running speed
图16是梁端处U型梁、F型轨和轨枕的竖向加速度幅值随行车速度的变化。由图16可见:当行车速度低于60 km·h-1时,U型梁、F型轨和轨枕的竖向加速度幅值随行车速度提高而变化很小;速度高于60 km·h-1后,U型梁和轨道的竖向加速度幅值均随行车速度提高而增大,其中F型轨竖向加速度幅值的增速较大。统计结果还表明:跨中处U型梁和轨道的竖向加速度幅值随行车速度的变化趋势与梁端处相似,不再赘述。需要指出的是,梁端处F型轨的竖向加速度幅值最大值达到5g,明显大于跨中处F型轨的竖向加速度幅值,原因是桥梁跨中竖向挠度达到了3.00 mm,这导致梁端处轨面的竖向折角较大。因此,当磁浮车辆以较高速度进出桥梁时将产生明显的竖向冲击,并导致梁端处F型轨的竖向加速度幅值明显增大。
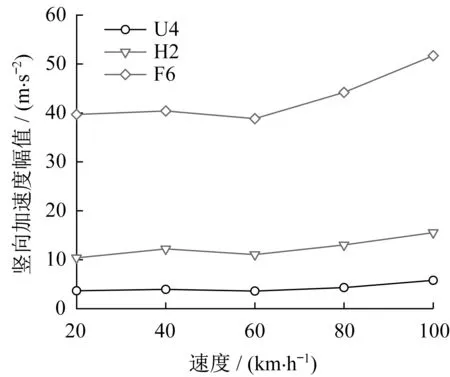
图16 梁端处U型梁和轨道竖向加速度幅值与行车速度的关系Fig.16 Relationship between vertical acceleration amplitude of U-type girder and track at the end and running speed
由于车辆二系悬挂系统具有良好的隔振性能,因此车体的竖向加速度幅值随行车速度的提高变化很小。在20~100 km·h-1速度工况下车体质心的竖向加速度幅值均很小,最大值不超过0.13 m·s-2,故不再细致分析。图17为悬浮模块的竖向加速度幅值随行车速度的变化。当行车速度不超过80 km·h-1时,悬浮模块的竖向加速度幅值随行车速度的变化很小;当行车速度进一步提高到100 km·h-1时,悬浮模块的竖向加速度幅值从约3.0 m·s-2增大到3.8 m·s-2,可能原因是车体发生了共振(车辆通过桥梁的频率接近车辆二系悬挂频率)。
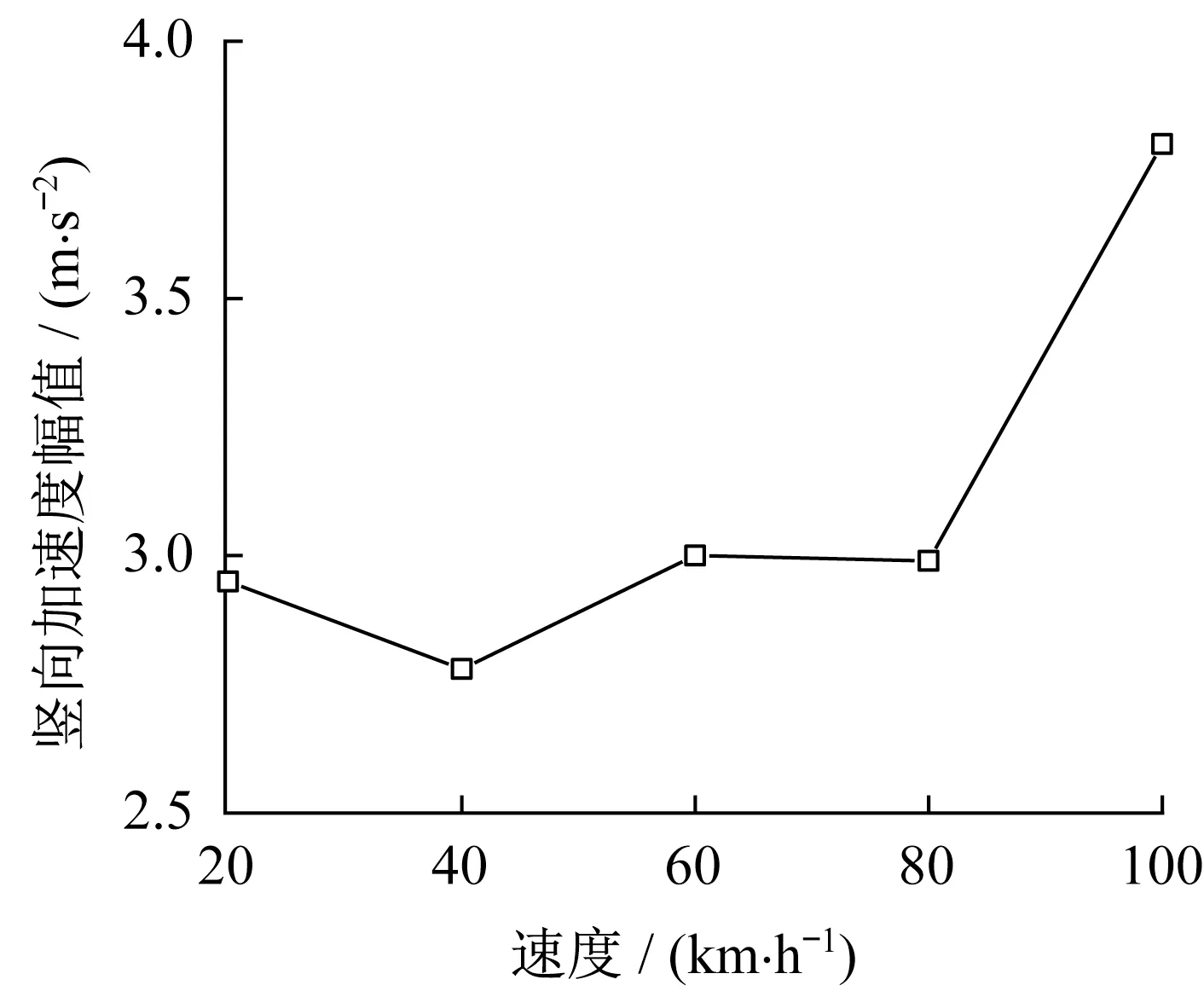
图17 悬浮模块竖向加速度幅值与行车速度的关系Fig.17 Relationship between vertical acceleration amplitude of levitation module and running speed
图18为单个电磁铁(每个悬浮模块包含4个电磁铁)悬浮力波动量随行车速度的变化。从图18可以看出:悬浮力波动量随行车速度增大而增大;速度为100 km·h-1时悬浮力波动量为1.56 kN,约占单个电磁铁额定悬浮力的19.5%,这说明磁/轨动力作用系数不超过1.2。电磁铁悬浮间隙波动量与行车速度的关系与悬浮力相似,速度100 km·h-1时悬浮间隙波动量为1.2 mm,这说明中低速磁浮列车能够在U型梁上安全、平稳地运行。
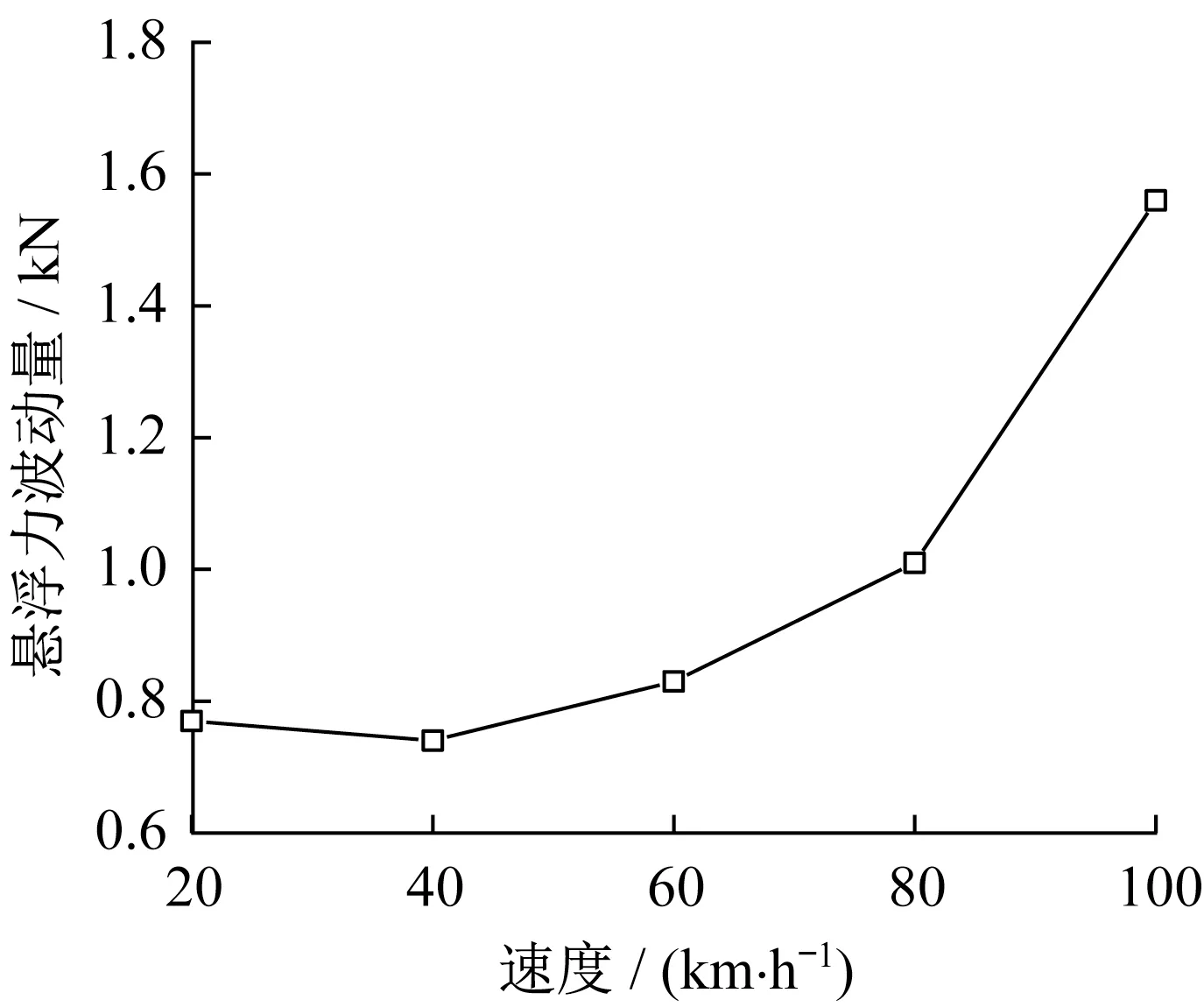
图18 悬浮力波动量与行车速度的关系Fig.18 Relationship between levitation force fluctuation and running speed
5 结论
(1)跨度25 m、梁高1.7 m的U型梁的一阶竖向自振频率为5.57 Hz,满足我国《中低速磁浮交通设计规范》对简支轨道梁频率限值的要求。轨道和U型梁结构的高阶模态伴随腹板扭转和呼吸模态,以及轨排局部振动模态,以轨排振型为主的轨道和U型梁结构的模态频率分布在40~70 Hz之间。
(2)行车速度为100 km·h-1工况下,U型梁的跨中竖向位移为3.00 mm,竖向挠跨比约为1/8 333,远小于《中低速磁浮交通设计规范》规定的挠跨比限值1/3 800;跨中处U型梁底板的竖向加速度最大值为1.03 m·s-2,F型轨的竖向加速度最大值为7.69 m·s-2,总体上U型梁及桥上轨道结构的振动响应不大。梁体竖向加速度响应的主频为5.59 Hz,与轨道和U型梁结构的一阶竖弯模态频率接近;F型轨竖向加速度响应的主频为55.44 Hz,与轨道和U型梁结构的第25阶模态(轨排模态)频率接近。
(3)磁浮车辆以20~100 km·h-1速度通过U型梁时,车体质心竖向加速度随速度提高变化不大,车体竖向加速度幅值很小,最大值不超过0.13 m·s-2;悬浮力波动量和悬浮间隙波动量随速度提高而增大,但绝对值均较小,悬浮间隙的波动量不超过1.0 mm,小于允许的间隙变化限值4.0 mm,中低速磁浮列车能够在U型梁上安全平稳运行。
(4)U型梁跨中竖向挠度和竖向加速度幅值随行车速度提高变化不大,但梁端处F型轨的竖向加速度响应随行车速度提高明显增大,行车速度100 km·h-1时梁端处F型轨的竖向加速度达到5g,这可能会降低梁端处轨道结构的可靠性和耐久性。

