基于影响矩阵法的钢管混凝土拱桥索力优化模型

邓宗仁，何楚韶，刘运思，杜宪武，杨玉平

（1.中铁北京局集团（天津）工程有限公司，天津 300000；2.湖南科技大学 岩土工程稳定控制与健康监测省重点实验室，湖南 湘潭 411201）

0 引言

钢管混凝土拱桥在拱肋中充填混凝土，可充分发挥混凝土的强度及提高其变形性能，同时也可以增强拱桥整体的稳定性。此外，钢管拱肋采用分节吊装拼接而成，能极大地缩短工期，同时也节省了混凝土浇筑模板的费用，使其在跨越50～200 m 的地形障碍时相较其他类型的桥梁具有明显的优越性。

系杆拱桥的施工中，张拉吊杆是十分关键的一环。吊杆的张拉一般分几个批次进行，后期的张拉会对前期的张拉效果产生影响，从而导致部分吊杆的受力不在控制范围内，这就会造成工期后延，成本增加。因此，如何确定合理的张拉力、张拉顺序，减少张拉的次数成为吊杆领域的研究热点。近年来，研究人员对这一领域进行了深入研究，成果颇丰。王祥国等[1]为优化吊杆张拉次数，结合影响矩阵法[2-3]，对吊杆的张拉模型进行了优化，并通过算例验证了模型的可靠性。任亮等[4]采用恒载“零弯矩”法计算拉索索力，并以优化恒载弯矩的分布为目标，对拉索索力进行了优化。何畏等[5]运用Ansys 对上承式拱桥进行了建模，通过调整最大悬臂状态下扣索索力来优化拱圈的应力。徐岳等[6]在影响矩阵法的基础上，结合正装差值迭代法来确定最佳的扣索索力。张治成等[7]以大跨度桥为例，引入最优化计算理论，并结合有限元模拟，有效解决了线性调整中的索力计算问题。胡常福等[8]提出了基于均匀设计影响面结合牛顿迭代的非线性索力优化方法，该方法运行效率较高，可有效减少计算时间，在新型索拱桥的索力优化中具有良好的适用性。傅金龙等[9]比较了几种索力优化方法及其适用性，并结合具体的工程实例进行了验证。

在上述研究的基础上，本文以东海特大系杆拱桥为例，基于影响矩阵法，构建了索力优化模型，以优化吊杆张拉次数为目标、以张拉力为变量，运用有限元分析软件搭建了桥梁模型，并对优化模型进行了可靠性验证，以期为同类工程进行索力优化提供一定的借鉴与参考。

1 优化模型的建立

1.1 影响矩阵法

1）受调向量。其为结构中控制截面上的k个独立元素组成的列向量，这些元素接受调整以达到某种期望的状态，记为

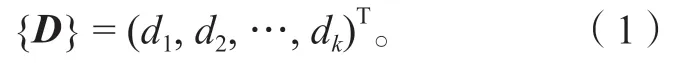
2）调值向量。其由结构中可以进行调整以改变受调向量的n（n＜k）个独立元素组成的列向量组成，记为

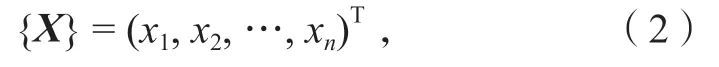
此处施调元素X为吊杆张拉力。

3）影响向量。其为施调向量X中第j个元素发生单位变化时，引起受调向量D的变化向量，记为

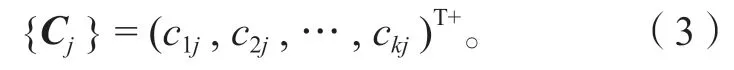
4）影响矩阵。n个施调向量分别发生单位变化，将得到的n个影响向量依次排列形成的矩阵即为影响矩阵，记为

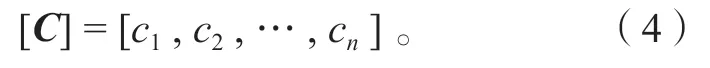
当结构满足线性叠加原理时，有

1.2 吊杆索力计算

目前针对吊杆内力计算的方法主要有如下两种：1）刚性支承连续梁法。按照刚性支承连续梁法确定吊杆内力时，以系梁的竖向变形作为控制目标，在保证成桥线型的状态下对系梁的内力进行优化，其局限之处在于未考虑拱肋的变形情况。2）刚性吊杆法。通过刚性吊杆法计算吊杆的张拉力时，拱肋会在吊杆索力的作用下与吊杆一起产生刚性位移，即吊杆与系梁的连接处将产生竖向挠度，所以这种计算方法也存在一定的局限性。

因刚性支承连续梁法和刚性吊杆法计算吊杆内力均存在一定的局限性，因此，本文拟在赵伟等[10]研究的基础上，结合影响矩阵法，采用刚性吊杆结合自动调索的综合分析索力方法，其具体分析过程如图1所示。

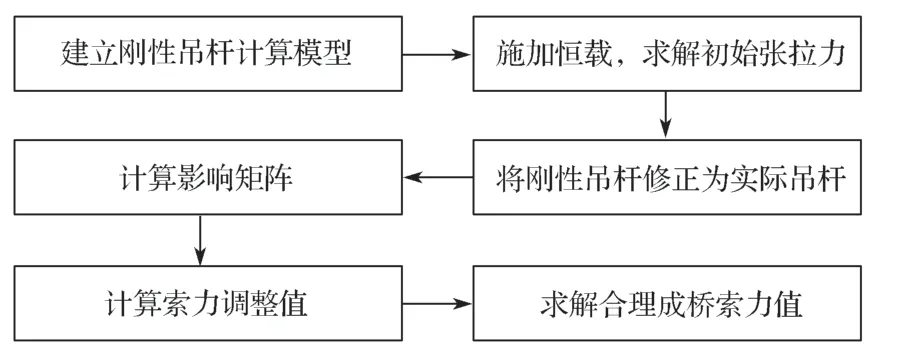
图1 索力计算流程图Fig.1 Cable force calculation flow chart

1.3 吊杆索力优化模型

目前，在施工过程中对索力进行调整的方法主要有影响矩阵法[2-3,11-12]和正装迭代法[13-14]。本文选用影响矩阵法来分析吊杆之间的索力影响关系，吊杆安装上去时处于无应力状态，对其施加初次张拉力，然后采取迭代的方式对索力值进行逐步调整，直至其逼近成桥索力设计值。在调整的过程中，最关键之处在于假定一个合理的初始张拉力，以使得各吊杆处于受力状态[15-16]。

在索力为P0的状态下，对应拱肋的弯矩分布向量为M0，它与期望状态时的拱肋弯矩分布向量M的差值为

此时若存在一组索力调整量ΔP，满足：

则索力调整量为

式中：P为优化后的索力；P0为优化前的索力。

对方程（7）进行求解，可以得到施工张拉索力调整值 ΔP。

索力调整之后，将实测索力与设计索力进行比较，若未达到控制范围内的精度，则在实测索力的基础上进行迭代计算，直至吊杆索力与设计值间的差值满足要求。

此外，为使索力受力处于合理状态，在调整的过程中须满足以下两个条件：

1）索力值必须为正，并且不超过其许用应力的40%；

2）相邻吊杆的索力值差不能过大，要满足索力的均匀性。

条件1）可表示为

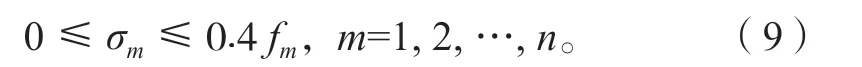
式中：σm为吊杆的应力值；fm为吊杆的设计强度值。

设相邻的吊杆索力值分别为F1、F2、F3，引入索力不均匀系数[4]：

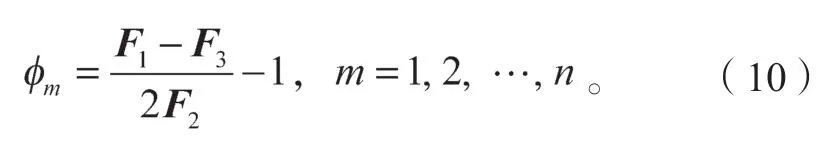
不均匀索力Zm为

对索力的不均匀性约束可表示为下式：

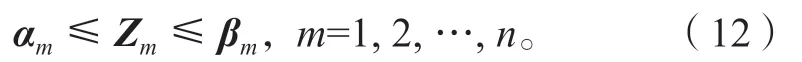
其中，αm和βm分别为不均匀索力的上限和下限,其具体取值可经过试算得到。

2 工程案例

2.1 工程概况

本工程中，主桥布置为（39.55+168.00+39.55）m 三跨连续梁-系杆拱，全长247.1 m。本桥结构体系为刚性梁、刚性拱。采用双吊杆结构，全桥共设18 组吊杆，吊杆顺桥向间距8 m，横桥向间距12 m，采用LZM（K）7-73（Ⅰ）型吊杆系统，PES（FD）低应力防腐索体，高强低松弛镀锌钢丝。上、下拱肋计算跨度分别为170.10,165.75 m，设计矢高分别为45,39 m，上、下钢管拱轴线均采用悬链线，系数分别为1.05,1.40。拱肋采用分段吊装拼接而成，内部填充混凝土。拱脚混凝土分两次现浇，在现浇第一次混凝土前，应将拱肋钢管、加劲钢材等安放到位，拱肋完成后浇筑第二次混凝土。两榀拱肋之间共设9道横撑，横撑均采用空间桁架撑，钢管内部不填混凝土，其内外表面均需做防腐处理。系梁为单箱三室等高箱梁结构。

2.2 桥梁建模

本研究采用有限元软件Midas Civil 建立拱桥的有限元模型。模型共计1 248 个单元，单元之间的连接形式分为一般支承和弹性连接两种，具体的连接方式如表1与图2所示。

表1 模型中各单元的连接方式Table 1 Connection mode of individual unit in the model

图2 桥梁模型各单元连接方式示意图Fig.2 Schematic diagram of the connection mode of individual unit of the bridge model

图2a 表示箱梁节段与节段之间采用弹性连接的方式进行连接，即建模时对两节段连接处的节点施加弹性连接；图2b 表示箱梁与底部的墩台和支架的一般支承连接方式；图2c 表示拱圈与拱圈支架的一般支承连接方式。

箱梁底部支架及拱圈支架布置立面图如图3所示，为简化模型，将箱梁底部的支架与拱圈支架简化为一般支承的连接方式，即对箱梁与底部支架连接处的节点、拱圈与拱圈支架连接处的节点，施加一般支承连接。

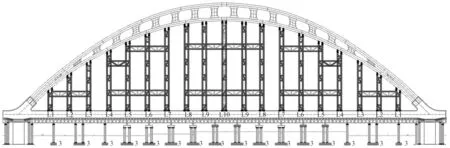
图3 箱梁底部支架及拱圈支架布置立面图Fig.3 Elevation view of bottom bracket with the arch ring bracket layout of box girder

表2为施工阶段的划分，表3为桥梁模型的材料参数，图4为桥梁有限元模型示意图。

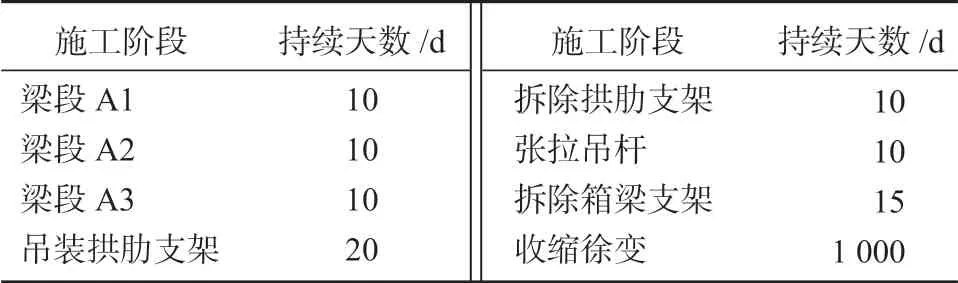
表2 施工阶段划分Table 2 Construction phase division

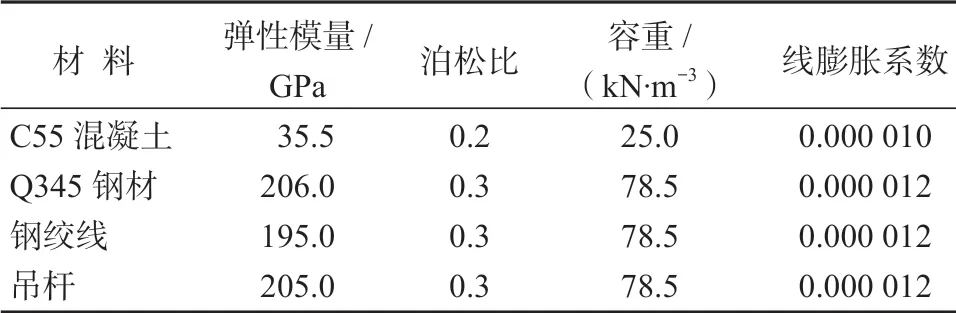
表3 桥梁模型的材料计算参数Table 3 Material calculation parameters of the bridge model

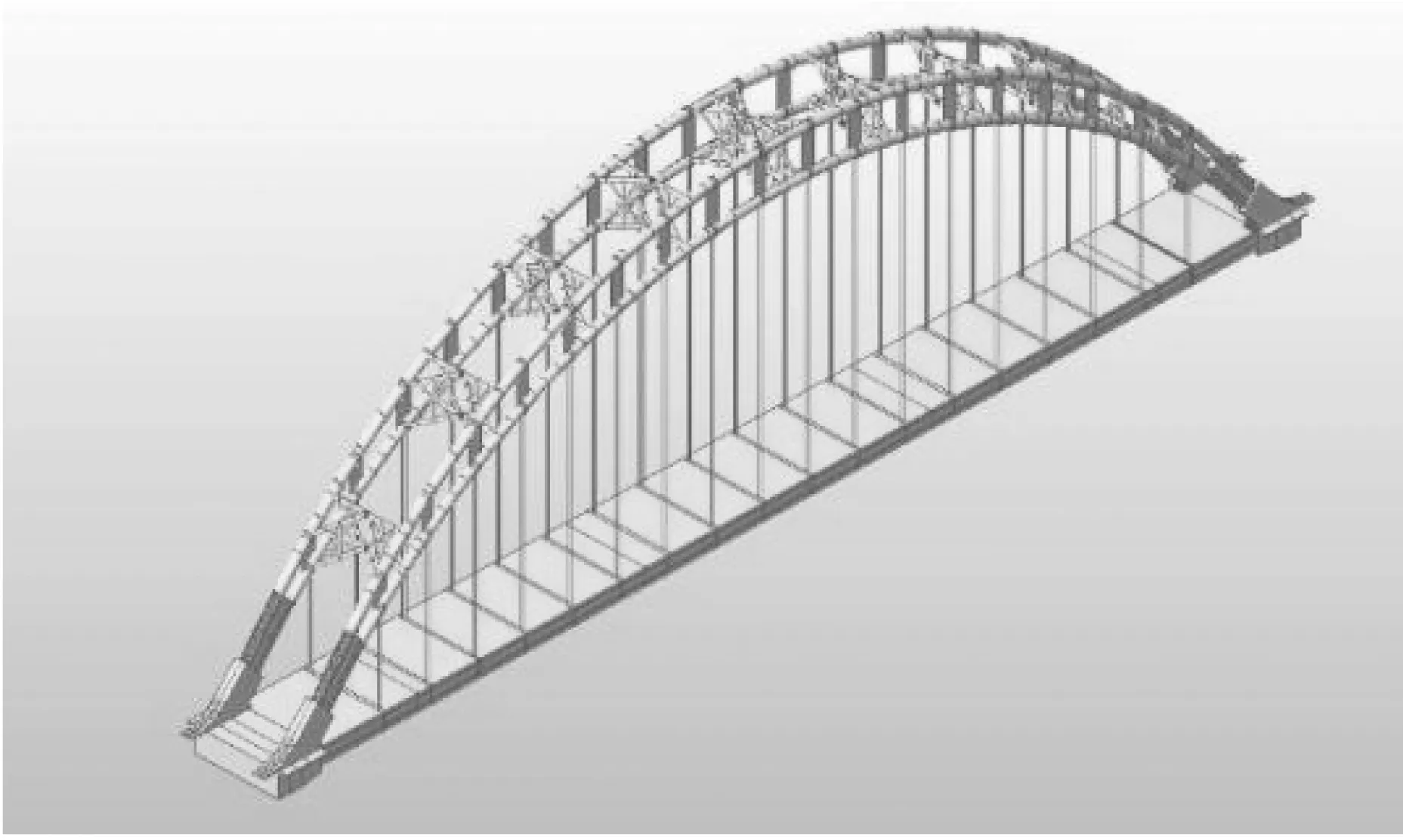
图4 拱桥有限元模型示意图Fig.4 Schematic diagram of arch bridge finite element model

模型荷载情况见表4，荷载组合为：

表4 模型荷载参数Table 4 Model load parameters

q恒×1.2+q活×1.4。

桥梁的施工阶段共分为8 个阶段，首先对系梁进行浇筑，从左至右等分为A1、A2、A3 共3 段进行浇筑；然后，进行拱脚浇筑；其次，进行拱肋的安装，而拱肋安装完成后即进行拱肋支架的拆除；接下来进行吊杆张拉；最后，拆除系梁底部的贝雷梁。

2.3 优化结果

本桥为对称结构，因此只需要取半幅进行研究。首先，基于1.2 节的方法，采用刚性吊杆法计算出吊杆索力值。将吊杆横截面积增大100 倍，同时将其质量减小为原来的1/100，近似为刚性结构，计算得到的吊杆索力值如表5所示。

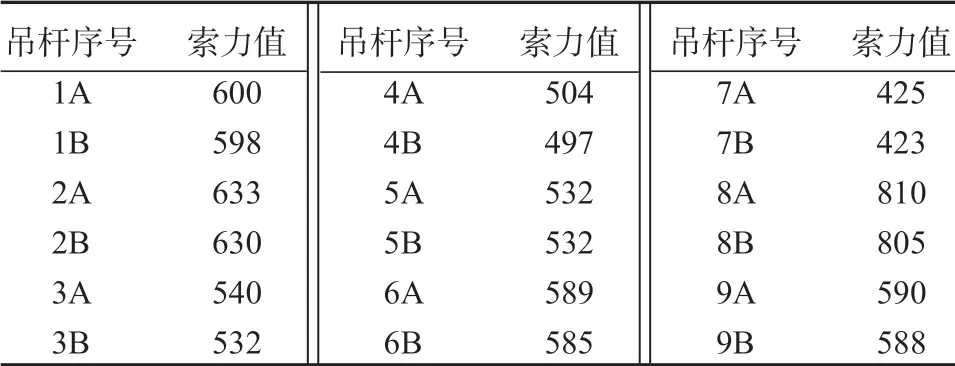
表5 刚性吊杆法计算得到的索力值Table 5 Cable force values by rigid suspender method kN

将表5中的索力值代入有限元模型，可得到成桥状态下的吊杆索力计算值P1，将其与设计索力值P0进行比较，可得到索力调整值：

然后由式（7）来计算施工张拉调整值。将调整后的索力值代入有限元模型，即可得到调整后的成桥索力计算值，如表6所示。

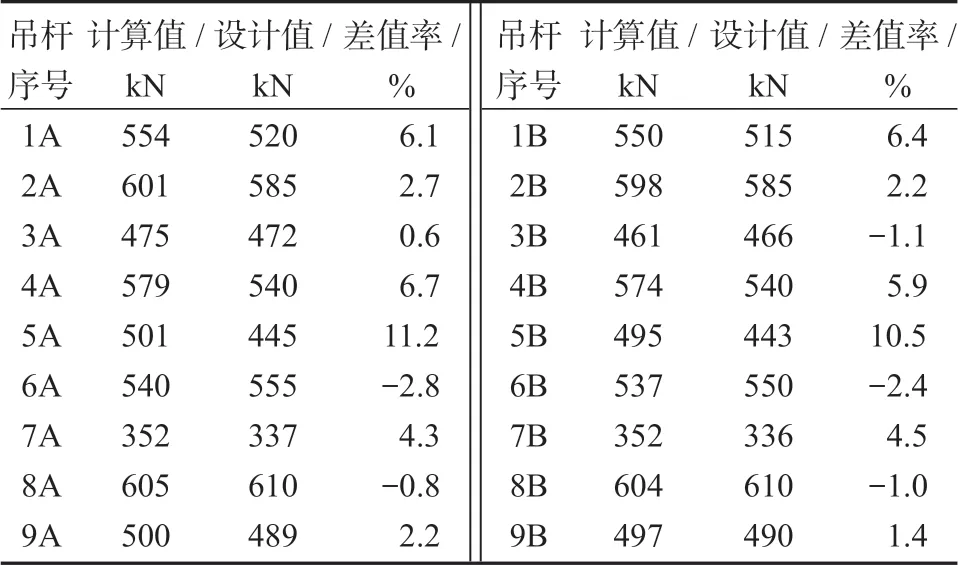
表6 第一次优化后的成桥索力值Table 6 Cable force values of the bridge after the first optimization

从表6中可以发现，成桥索力计算值和设计值差别最大处为5A 和5B，差值率分别为11.2%,10.5%。在实测索力的基础上，进行迭代计算，得到第二次优化的吊杆施工张拉力，如表7所示。

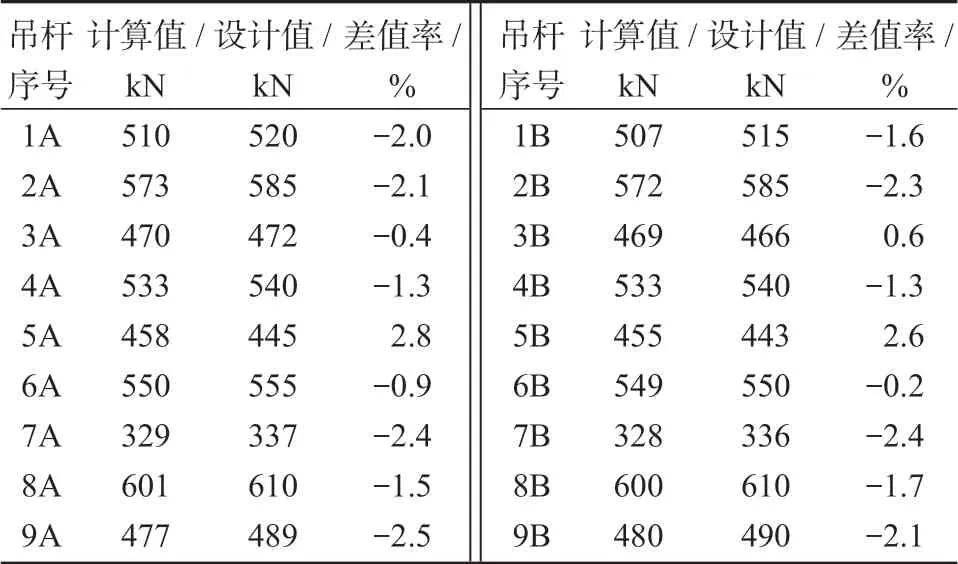
表7 第二次优化后的成桥索力值Table 7 Cable force values of the bridge after the second optimization

图5所示为优化后计算索力与设计索力的差值率。由图可知，经过两次优化后，成桥索力与设计索力的差值率控制在±3%的范围内，满足施工控制要求。

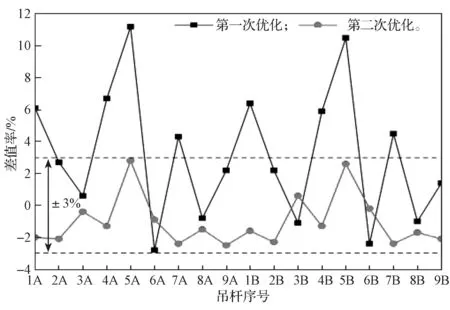
图5 刚性结构吊杆的计算索力与设计索力差值率Fig.5 Difference between the calculated cable force and the design cable force of the rigid structure suspender

本研究同时采用王新征等[14]基于正装迭代法及最小二乘法原理所建立的索力优化模型，对本项目进行索力优化，所得计算索力与设计索力的差值率结果如图6所示。由图6可以发现：在第一次索力优化过程中，造成的最大误差率为13%；在第二次优化过程中，造成的最大误差率为8%，而本文所建立的索力优化模型，经过两次优化后，能将误差率控制在±3%的范围之内。

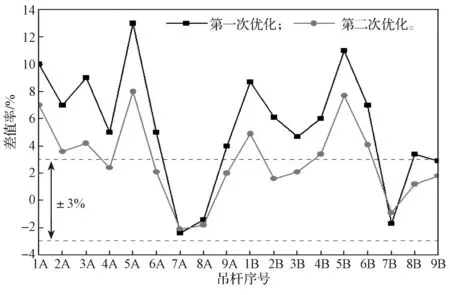
图6 文献[14]中优化模型的计算索力与设计索力差值率Fig.6 Difference between the calculated cable force and the design cable force of the optimized model in literature [14]

通过有限元模型，可得成桥状态下拱桥各部位的变形情况。图7～9 分别为系梁、上拱肋和下拱肋不同位置处的设计挠度值与优化后挠度值变化曲线。

由图7～9不难发现，经过两次优化后，进行张拉的系梁挠度与设计的系梁挠度大致相同，两者差别最大的地方发生在距系梁中心的水平距离48 m 处，差值为6.04%。此外，优化前后上下两榀拱肋的竖向挠度也基本一致，两者差别最大的地方分别发生在距拱肋中心的水平距离48 m 处和52 m 处，差值分别为6.57%,4.80%。

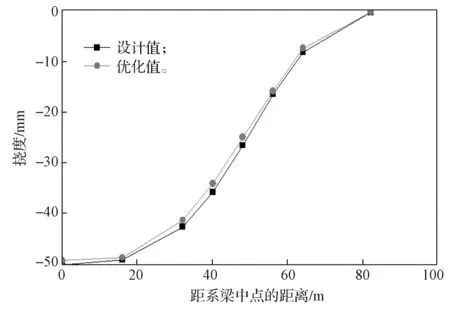
图7 系梁恒载挠度曲线Fig.7 Tie beam dead load deflection curves

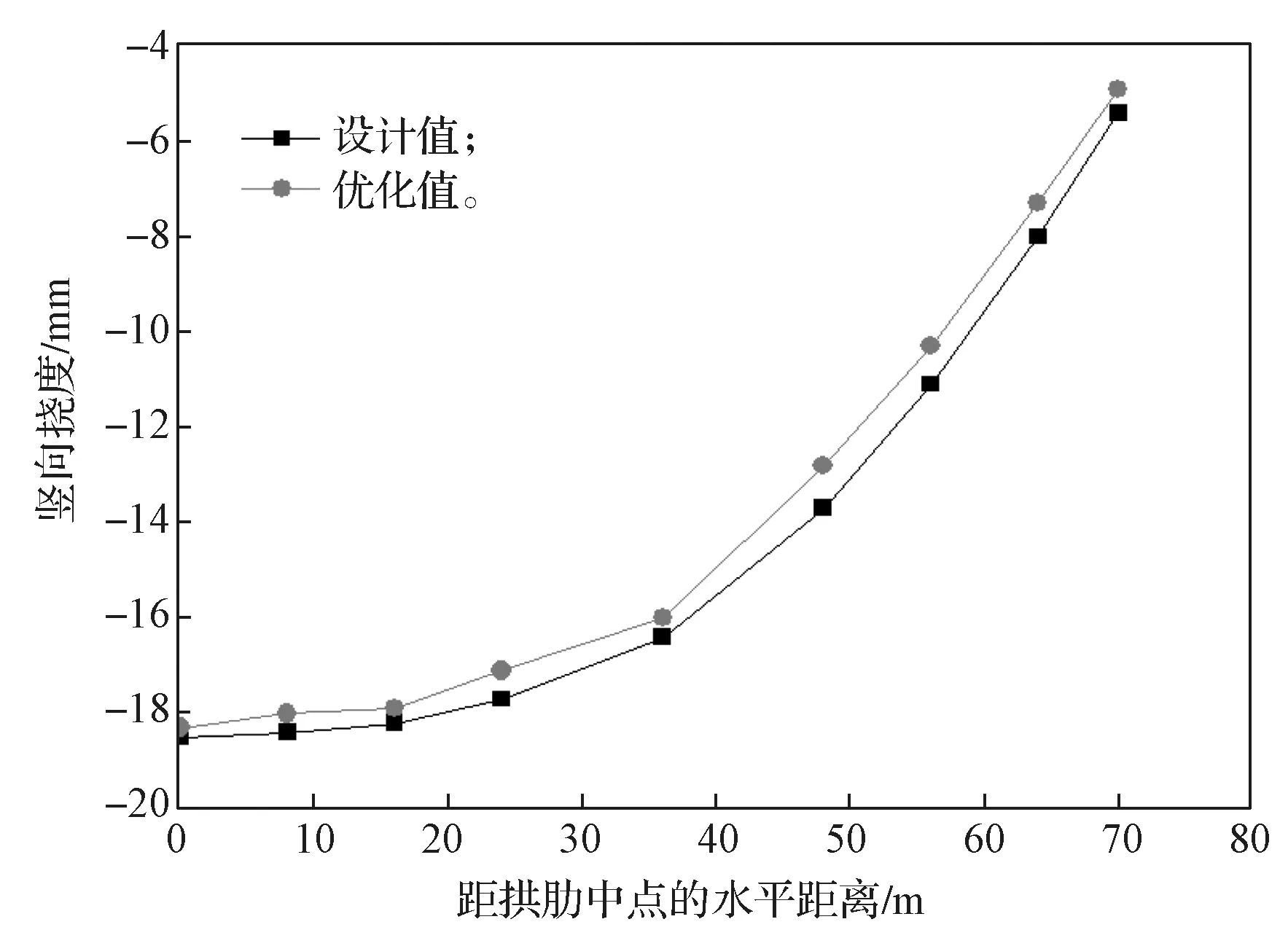
图8 上拱肋恒载挠度曲线Fig.8 Dead load deflection curves of the upper arch rib

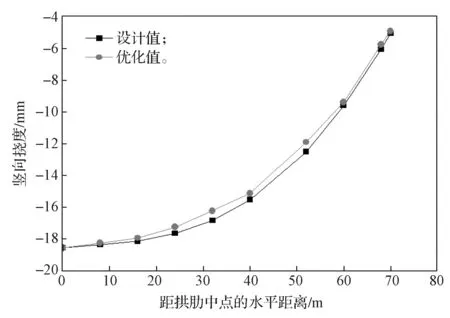
图9 下拱肋恒载挠度曲线Fig.9 Dead load deflection curves of the lower arch rib

3 结论

本文结合东海特大桥系杆拱连续梁，在影响矩阵法的基础上，以优化吊杆张拉次数为目标，建立了吊杆的索力优化模型，同时运用Midas Civil 建立拱桥的有限元模型，对索力优化模型的可靠性进行了验证，研究结果表明：

1）经过两次对施工张拉索力进行调整后，吊杆的成桥索力值与设计索力值的差值控制在±3%的范围之内，满足施工控制要求；

2）成功地将吊杆张拉次数缩减为两次，大大缩短了工期；

3）优化后上下拱圈及系梁的变形量与设计挠度基本相同，差别最大的为6.57%。

此外，本模型在构建的过程中没有将拱肋的轴力纳入约束条件，在接下来的研究中，可以考虑将其作为约束条件，对张拉模型进行完善。