基于颗粒法的物质热传导建模与可视化仿真

陈晓峰，黄刚海，邱泓杰

（1.湖南科技大学 岩土工程稳定控制与健康监测湖南省重点实验室，湖南 湘潭 411201；2.湖南科技大学 土木工程学院，湖南 湘潭 411201；3.中南大学 土木工程学院，湖南 长沙 410075；4.中南大学 资源与安全工程学院，湖南 长沙 410075）

1 研究综述

颗粒材料与人们的日常生活密切相关，如土壤、砂石、粮食等。颗粒材料的热传导研究有着广泛的应用前景。如在核废料地质处置中，深埋地下核废料中的核元素衰变会释放大量热，通过热传导使围岩温度升高，由热应力引起的围岩破裂可能导致核废料泄漏，污染水资源；地热具有清洁、可循环和安全等优点，是较好的可再生能源之一。在地热开采中，将冷水注入热岩，使岩石温度下降，导致岩石发生热破裂，这一问题也涉及岩石热传导。此外，地壳中矿床的形成规律研究、矿床勘探、二氧化碳的地质存储和油气开采等新领域都与颗粒材料热传导联系紧密。因此，对颗粒的热传导研究有着重要的应用价值。

颗粒系统热传导问题研究分为两类，即连续介质传热模型和离散颗粒传热模型。连续介质传热模型将系统的宏观性质及宏观传递过程与微观结构、微观特性相联系，常用的有由I.Nozad 等[1]提出的有效介质法，用各向同性的有效介质代替颗粒系统，将材料的微观结构特性简化得到平均温度分布，其不足之处在于忽略了颗粒系统的高度离散性；相反，基于微观层次用离散模型研究颗粒材料的传热过程不存在此类问题。对于离散颗粒传热模型，S.Yagi等[2]最先提出了离散颗粒传热的概念，认为颗粒之间可通过5 种途径传热。针对各传热途径之间的差异，学者们提出了多种模型及相应的计算表达式。如M.Yovanovich[3]指出，接触面间的导热是颗粒系统传热的主要方式。Sun J.等[4]将两颗粒通过接触面的导热问题近似为两个半无限厚介质间的热传递问题，但作了过多简化。W.L.Vargas 等[5-6]研究发现，在理想情况下，接触面上传递的热量与颗粒间的法向应力存在一定的函数关系，在此基础上发展了热颗粒动力学法（thermal particle dynamics，TPD），但其在计算非固定颗粒时具有局限性。B.Chaudhuri[7]利用离散单元法（discrete element method，DEM），结合TPD，对转鼓中颗粒在转动情况下的传热问题进行了研究。Shi D.L.[8]结合DEM 与计算流体动力学（computational fluid dynamics，CFD），模拟了不同材料、不同颗粒大小情况下回转窑中颗粒的导热问题。Feng Y.T.等[9-10]以两个颗粒间的接触为基本单元，将颗粒体模型化为传热网络，发展了颗粒材料中热传导问题的离散温度单元法（discrete thermal element method，DTEM），并对较大规模的二维颗粒系统导热问题进行了研究，但其计算传热需要引入两个未知量。颗粒法（particle simulation method，PSM）将介质材料离散为一系列通过接触连接在一起的颗粒结合体，可用于求解颗粒材料的热传导问题，已发展了成熟的颗粒法软件PFC（particle flow code）[11]，现已被广泛应用于颗粒材料特性及各类工程问题研究中。

与此同时，国内也有学者开展了关于颗粒热传导方面的研究。刘安源等[12]在分析颗粒碰撞传热机理的基础上建立了一个新的颗粒碰撞传热理论模型，对流化床内床层与壁面的碰撞传热系数进行颗粒层次上的模拟。武锦涛等[13]综合考虑颗粒接触传热的多个过程，提出了颗粒接触传热模型，并结合DEM模拟了移动床中颗粒与加热面间的传热过程。李腊梅等[14]提出了一种全新的非连续介质热传导数值计算方法，并通过自主编制计算程序验证了其正确性。于庆波等[15]采用CFD 软件，对颗粒绕圆管传热现象进行了建模，并验证了模型的正确性。王擎等[16]将离散元方法与颗粒热传导模拟结合，研究了回转干馏炉内颗粒间的传热过程。姬国钊等[17]通过离散元方法分析了回转窑内颗粒的运动和换热过程。

从国内外研究现状看，热传导的研究常采用商业软件模拟，独立开发自主计算程序甚少。而对热传导研究方法而言，离散颗粒模型，因考虑了实际颗粒组成结构，能更好地反映实际过程，受到了更广泛的关注。鉴于热传导研究现状及离散颗粒模型的优点，本论文以颗粒法为传热算法，自主编写C++代码，开发热传导计算程序，对颗粒材料进行热传导建模及可视化仿真分析。

2 颗粒法基本原理

2.1 热传导基本方程

设颗粒系统中任一颗粒为单元i，温度的变化规律满足连续介质热传导方程：

式中：ρi为颗粒密度；Cv为材料比热容；qi为热流密度；qv为单位体积发热率；Ti为颗粒温度。

傅里叶热传导定律定义了热流密度与温度梯度间的关系：

式中：x为热流方向；k为热传导系数。

常用的边界条件分为3 类：

1）Dirichlet 边界，指定边界上的温度值。

2）Neumann 边界，指定边界上的热流密度值。

3）Robin 边界，指定边界上的对流换热系数及边界层温度值。

本研究中将颗粒材料离散为一系列的热存储器和热管道，热量将通过热存储器之间的激活管道进行传递。热管道的有效性与接触有关，如果接触过程中两颗粒单元有重叠则认为连接两颗粒间的热管道有效，热传导接触模型示意图如图1所示。

图1 热传导接触模型示意图Fig.1 Schematic diagram of heat conduction contact model

从图1所示模型可知，热管道连接两个热存储器，热流仅在热管中流动，两热存储器转移的热量即为热管的能量ΔQ，热管有固定的热阻η，将每个热管看成单位长度上热阻为η的一维物体，则有：

式中：ΔT为热管道两端热存储器的温度差；L为热管道的长度。

对颗粒单元i进行分析，可得：

式中：ηi-j与Li-j分别为连接单元i与单元j间热管的热阻与长度。

同理可得：

测量颗粒单元中热传导系数与热管道中的热阻抗系数有如下理论关系式[11]：

式中：p为颗粒材料的孔隙率；V为颗粒的体积。

2.2 热传导数值离散

给定初始条件下的温度，可计算出每个热管的能量变化量，从而热源的温度将改变，变化公式如下：

对式（10）中时间导数向前差分，可得：

式中Δt为时间步长。

2.3 热传导计算流程

基于上述颗粒法基本原理和热传导接触模型，通过所有接触对热传导的累积，可实现整个颗粒系统的热传导。计算流程如图2所示，其中i_step为计算步标识，i_par为颗粒单元标识。每执行一次循环更新一次颗粒单元温度，当达到时间总长时输出结果，计算结束。

图2 热传导计算流程图Fig.2 Calculation flow chart

3 可视化模型建立

热传导的程序架构和软件界面如图3所示。程序主要分为计算内核模块和可视化模块两部分。

图3 热传导程序架构和软件界面Fig.3 Program architecture and software interface

计算内核模块将热传导相关数据和操作封装成一个C++类——CHeatConduction 类，用于执行所有与圆盘颗粒热传导有关的运算。CHeatConduction 类的数据结构如图4所示。

图4 CHeatCondution 类数据结构Fig.4 Data structure of CHeatCondution

由图4可知，该类用小类对象作为其成员变量，主要包括CDisk 类——圆盘类，每个CDisk 类对象表示圆盘颗粒系统中的一个圆盘；其成员变量主要包括圆盘温度和圆盘温度变化量，圆盘中心坐标和半径；圆盘密度和质量以及与该圆盘接触的相邻圆盘数据等。pD 为CheatConduction 类对象数组，存储了圆盘颗粒系统中所有圆盘的数据。

热传导计算主要包含如下操作。

Step 1 执行setInitialTemperature( )函数，设置初始温度；

Step 2 执行searchContactPairs( ) 函数，访问pD 数组，搜索系统中的所有圆盘-圆盘接触对，根据接触对数据求解出与传热有关的变量(如嵌入量等)；在计算中以上步骤只需执行一遍，这是因为本论文中颗粒固定不动，因此颗粒间的接触方式及与传热有关的嵌入量等均保持不变。然后执行单位时步的计算，每一单位时步内的计算分为两步：

Step 1 执行implementCalculation( )函数，求解每一组接触对的温度变化量，更新改变后的圆盘温度值，并将求解结果保存至圆盘数组中；

Step 2 执行updateModelData( )更新颗粒温度。

其中，可视化模块被封装成了另一个C++类——COpenGL 类，该类从Qt 预定义的QOpenGLWidget类和QOpenGLFunctions 类派生，并重写其内嵌虚函数，用于渲染程序界面的可视化视窗。CHeatConduction 类和COpenGL 类通过指针相互访问，COpenGL类可读取CHeatConduction类的数据（如颗粒的温度、位置坐标及颗粒大小等）并将模型实时显示在计算机屏幕上。

4 模型验证与结果分析

通过分析一维薄板、二维对称圆环的热传导特性对其进行正确性验证。本研究算例所用参数如下：热传导系数k=1.6 W/(m·℃)；比热容Cv=0.2 J/(kg·℃)；密度ρ=1 000 kg/m3；初始温度T0=0 ℃。

4.1 一维薄板热传导

一维平面薄板热传导示意图如图5所示。由图5a 可知，平面薄板的长度L=20 m，宽度W=0.2 m。采用100 个圆盘搭建一维薄板热传导模型。模型左右两侧设定不同的常温度边界，分别为T1=100 ℃，T2=0 ℃。

图5 一维薄板热传导模型与变化规律Fig.5 One-dimensional thin plate heat conduction

该薄板在固定温度边界下逐渐达热平衡状态。根据文献[18]在“常温度边界下薄板的瞬态热响应”中的推导，薄板各处的温度T(Z,t)为

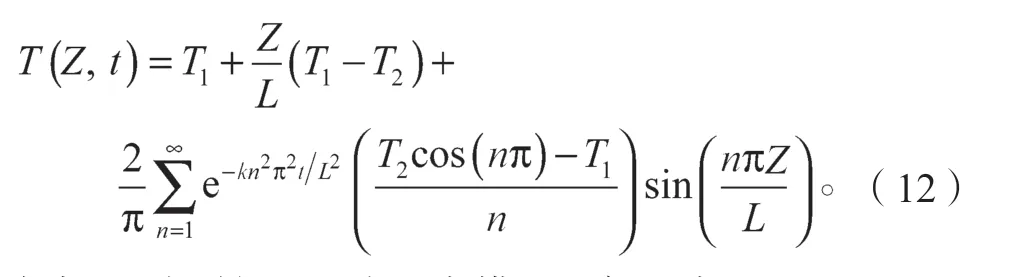
式中：t为时间；Z为距离模型左侧距离。

图5b 展示了自主程序算出的薄板各处温度及对应的解析解，可看出数值解与理论解高度吻合。

4.2 二维对称圆环热传导

二维对称圆环热传导示意图如图6所示。

图6a 可知，圆环的内径Ra=2 m，外径Rb=5 m，该模型由6 596 个半径为0.05 m 的圆盘组成。在模型内、外侧分别设定100 ℃，0 ℃的常温度边界。

由图6a 中的圆环模型，当热流稳定时各处温度T(r)的解析解[18]为

式中r为监测点到圆心的距离。

图6b 为自主程序计算出的圆环各处温度及对应的理论解，从中可以看出数值解与理论解高度吻合。

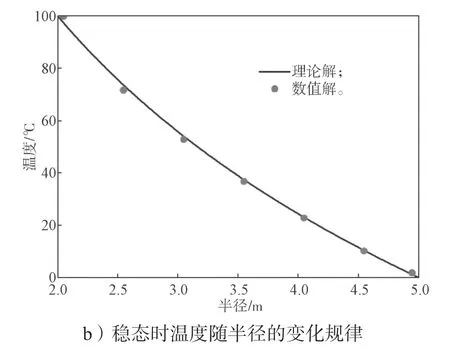
图6 二维对称圆环热传导模型与变化规律Fig.6 Two-dimensional symmetrical ring heat conduction

从以上一维薄板及对称圆环两个算例的结果可以看出：自主程序计算正确，且精度较高。

4.3 影响因素分析

4.3.1 颗粒粒径

图7为粒径不同的两个颗粒模型，在模型左右两侧分别设定100 ℃和0 ℃常温度边界进行热传导模拟。对两个模型分别监测，取监测点的位置为距离模型左侧4,8,16 m 处，所得结果如图8所示。从图8中的曲线图可以看出：颗粒半径对传热的影响非常小，大颗粒模型传热略快，但颗粒系统最终的稳定传热状态不受颗粒粒径的影响。

图7 两种不同粒径的颗粒模型Fig.7 Two particle models with different particle sizes

图8 颗粒粒径对传热的影响Fig.8 Influence of particle size on heat transfer

4.3.2 堆积方式

本研究建立了3 种不同的颗粒堆积模型，如图9所示。在堆积方式不同的3 种颗粒模型左右两侧分别设定100 ℃和0 ℃常温度边界，进行热传导模拟。对3 种模型取不同的位置点分别进行监测，所得结果如图10 所示。从图10 可以看出：堆积方式对传热的影响非常小，方形堆积传热略快，但颗粒系统最终的稳定传热状态不受颗粒堆积方式影响。

图9 3 种堆积方式的颗粒模型Fig.9 Disks model formed by three stacking methods

图10 堆积方式对传热的影响Fig.10 Influence of stacking mode accumulation methods

5 结论

本文讨论了模拟颗粒材料热传导的颗粒法接触模型、接触热交换计算方法及可视化实现算法的基本实施步骤。在此基础上，通过分析一维薄板、二维对称圆环的热传导特性，验证了模型的正确性。然后分析了颗粒粒径、堆积方式对传热的影响，得出如下结论：1）在其他参数一致时，颗粒半径对传热的影响非常小，大颗粒模型传热略快，但颗粒系统最终的稳定传热状态不受颗粒粒径影响；2）颗粒堆积方式对传热的影响较小，方形堆积传热略快，但颗粒系统最终的稳定传热状态不受颗粒堆积方式影响。

以上研究结果表明，所提方法能较好地模拟颗粒的热传导，但本研究也有一定局限性，仅对一维薄板、二维圆环进行了研究，对三维立体颗粒物质的传热还有待进一步研究。