基于数字图像相关和声发射的岩质锁固段破坏试验研究

范 杰，朱 星,*，霍冬冬，胡桔维，刘俊峰

(1.地质灾害防治与地质环境保护国家重点实验室，成都 610059；2.成都理工大学信息科学与技术学院，成都 610059)

大型岩质滑坡是一种具有极强突发性、破坏性和影响范围广的地质灾害，其中大部分大型岩质滑坡的整体稳定性受软弱结构面或剪切带上“锁固段”关键岩体的控制，此类滑坡被称为锁固型滑坡[1-3]。其中，“三段式”滑坡是由前缘蠕滑导致后缘拉裂，引起锁固段剪断破坏的典型锁固段型滑坡类型，是中国西部地区常见的岩质滑坡地质灾害[4-5]。

在“三段式”锁固段型岩质滑坡的研究方面，Huang等[6]通过声发射技术研究了大型岩质滑坡的起动机理，表明岩质滑坡的起动机制主要是受锁固段的控制。唐鹏等[7]通过相似材料建立锁固段滑坡的物理模型，从定性和定量的角度对锁固段的变形破坏进行了研究分析，表明锁固段的破坏是脆性剪切破坏。黄达等[8]对不同岩桥角大小对锁固段的破坏模式及演化规律进行了分析，随着锁固段岩桥角增大，锁固段区域拉应力的影响范围逐渐减小，由全部受拉向全部受压转变。

由于锁固段岩体损伤破裂伴随着能量应力波(微震、声发射)的释放，近年来声发射技术已逐渐应用于室内岩石破裂的机理研究。研究表明声发射参数AF(平均频率)值与RA(上升时间/振幅)值的比值可用作拉伸裂纹与剪切裂纹的破裂模式判识标准[9-11]。但是，对拉伸裂纹与剪切裂纹分界线斜率的定义仍依靠经验或者两者之间的最佳过渡线。为解决分界线不确定问题，甘一雄等[9]通过对比破坏过程中的RA与AF值分布的变化，与矩张量分析结果相互印证，从而获取两者的分界线斜率；Niu等[11]通过核密度估计(kernel density estimation,KDE)函数评估了裂纹分类的充分性；Zhang等[12]对代表性样品中的AE波形数据进行频谱分析，通过AE波形的主频特性，以确定拉伸裂纹和剪切裂纹的比率。分类问题及算法是机器学习的重要应用，其中支持向量机(support vector machine,SVM)是基于统计学的VC(Vapnik-Chervonenkis)维理论与结构风险最小原理的有监督判别分类器[13]，Alireza等[14]使用SVM根据AE参数特征对混凝土中的裂缝进行分类；Kumar等[15]使用高斯混合模型(Gaussian mtxture model,GMM)对收集的声发射(acoustic emission,AE)特征进行聚类后，根据SVM计算的最佳超平面将其分离，确定拉伸和剪切破坏事件的相对数量。就目前研究情况看[6-8]，锁固段破坏失稳研究仍集中在宏观破裂机制上，不能较好地分析锁固段破裂过程中微观、细观等破裂信息，不利于锁固段破裂失稳前兆特征分析和实时预警的实现，传统的岩石破裂模式判识方法[11-12]也具有较强的主观导向性。

为此，对“三段式”锁固段物理模型滑移段进行了单轴压缩试验，模拟潜在滑体的自重作用。采用AE与数字图像相关技术(digital image correlction,DIC)技术获取试验全过程的微破裂事件声发射波形信号和高清数字图像，通过声发射b值统计分析锁固段破裂尺度及阶段规律，利用机器学习的聚类分析微破裂模式并建立分类判据，结合DIC综合查明锁固段变形破坏全过程时空演化规律，以期为岩质滑坡锁固段失稳破坏提供一种科学有效的预警方法。

1 试验研究

1.1 试验方案

试验装备如图1所示，主要包括：WHY-1000微控压力试验机、工业相机、锁固段均质模型、传感器及采集装置。其中，锁固段模型参考文献[8]对“三段式”锁固段滑坡破坏模式研究，尺寸为250 mm×250 mm×150 mm。相似材料，水泥、石灰、砂、水的质量比为5∶1∶13∶4。滑坡模型后缘预制裂隙，锁固段岩桥角为90°，前缘蠕滑段填充有低强度材料石蜡，自然养护30 d，裂隙布置及几何参数如表1所示。

表1 裂隙布置参数Table 1 Fissure layout parameters

加载方式如图2(a)所示，为模拟潜在滑体的重力作用，在后缘拉裂隙以外部分施加荷载，加载速率为80 N/s。声发射探头通过凡士林耦合在锁固段上部(传感器s1)、中部(传感器s2)与下部(传感器s3)，采样频率为1 MHz。同时，试验过程中使用工业相机以75帧/s的速度、2 448×2 048的像素记录下模型破裂的整个过程。图2(b)为试验完成后物理模型的破坏情况。

图2 物理模型Fig.2 Physical model

1.2 研究方法

1.2.1 基于b值分析的变形破坏阶段界定

声发射b值最早源于地震学中地震活动震级和频率的G-R(Gutenberg-Richter)关系[16]，可作为衡量岩石内部小尺度微破裂事件和大尺度微破裂事件的判断指标，被广泛用于岩石破裂前兆的分析和判定[17-19]。研究表明，b值的降低表明以大尺度微破裂事件为主导特征；b值的增大表明以小尺度微破裂事件为主导特征[18]。通过最小二乘法计算b值，其计算公式为[16,20-21]

lgN=a-bM

(1)

M=lgA

(2)

式中：M为单个声发射事件震级；A为单个声发射事件的最大振幅，dB；a为经验常数；N为声发射事件累计次数。

1.2.2声发射特征参数获取及分析

不同的破裂机制以不同形态特征的声发射释放能量，中外部分研究成果[9-12]建立了如图3所示的材料破裂机制判定准则，微破裂所产生声发射信号的RA值增长与AF值降低指示着裂纹从拉伸破坏到剪切破坏的过渡[12]。通过探测和分析声发射事件信号的上升时间、持续时间、最大振幅和计数等特征参数，通过计算RA和AF特征参数来区分拉伸破裂和剪切破裂该特征参数的计算公式为[9]

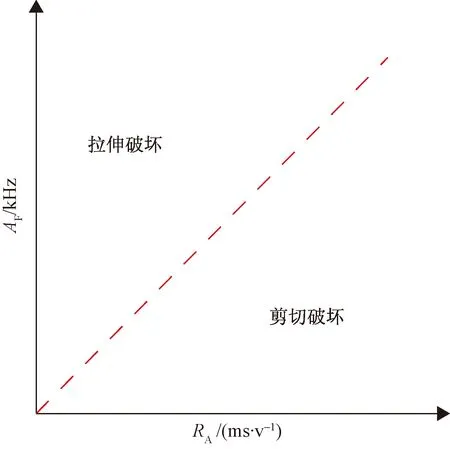
图3 AE参数裂纹分类方法Fig.3 AE parameter crack classification method

(3)

(4)

式中：RT为一次声发射事件中第一次计数到最大振幅的时间；C为一次声发射事件的振铃计数；D为一次声发射事件的持续时间。

1.2.3 基于GMM与SVM的声发射特征非监督分类方法

支持向量机是一个功能强大的监督性机器学习模型算法，由于其良好的泛化性能而被广泛用于模式识别问题[14]。其算法学习策略就是间隔最大化，间隔最大化的目的是增加模型的鲁棒性和泛化能力[22]。如图4所示，在间隔边界以外的地方增加更多实例不会对决策边界产生影响，即完全由间隔边界上的实例所决定，该实例被称为支持向量，支持向量尽可能远离决策边界。假设给定一个特征空间上的训练数据集，可表示为

图4 SVM分类超平面Fig.4 Hyperplane obtained by SVM

T={(X1,Y1),(X2,Y2),…,(Xn,Yn)}

(5)

式(5)中：Xi∈X=Rn；Yi∈Y={+1,-1}；Xi为第i个特征向量；Yi为Xi的类标记，当它为+1时为正例，为-1时为负例。

当训练数据集线性可分时，存在无穷多个分离超平面可将两类数据分开，感知机利用误差分类最小策略求得无穷多个分离超平面，SVM将利用间隔最大化求得唯一的最佳超平面(决策边界)。分离超平面及相应的分类决策函数为

w*x+b=0

(6)

f(x)=sinn(w*x+b)

(7)

式中：w*为法向量；b为截距。

1.2.4 基于数字图像的微应变分析方法

数字图像相关技术(digital image correlation，DIC)是一种依据试样变形前后的两幅数字图像，通过相关计算获取感兴趣区域的变形信息的高精度非接触式的测量方法[23-24]。通过DIC探测及分析锁固段区域的微应变及裂隙发展演化趋势。其基本原理如图5[20]所示，将参考图像划为多个大小相同的子集，随后在变形图像中对变形子集进行跟踪，其计算公式为[25]

(8)

xcuri为变形图像子集的x坐标；xrefi为参考图像子集的x坐标；u为子集中心的水平方向的位移分量；xrc为参考图像的x坐标至变形图像的的x坐标转换；xrefc和yrefc为参考图像子集的中心坐标；ycurj为变形图像子集的Y坐标；Yrc为参考图像的Y坐标至变形图像的的y坐标转换图5 DIC微应变监测原理图[20]Fig.5 Schematic diagram of DIC micro strain monitoring[20]

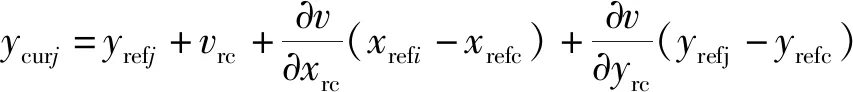
(9)

(10)

式(10)中：P为广义的变形矢量。

2 试验结果

2.1 锁固段破裂失稳声发射特征及演化

2.1.1 基于b值统计的变形破坏过程阶段划分

根据试验过程中声发射数据采集频率，设置单个声发射b值计算样本间隔为10 s。图6(a)所示了锁固段物理模型加载全过程声发射b值统计的演化曲线。结合时间荷载曲线及已有岩石破裂过程分类研究[26]，模型在加载过程中裂隙的萌生、扩展与贯通过程大致可分为以下4个阶段。

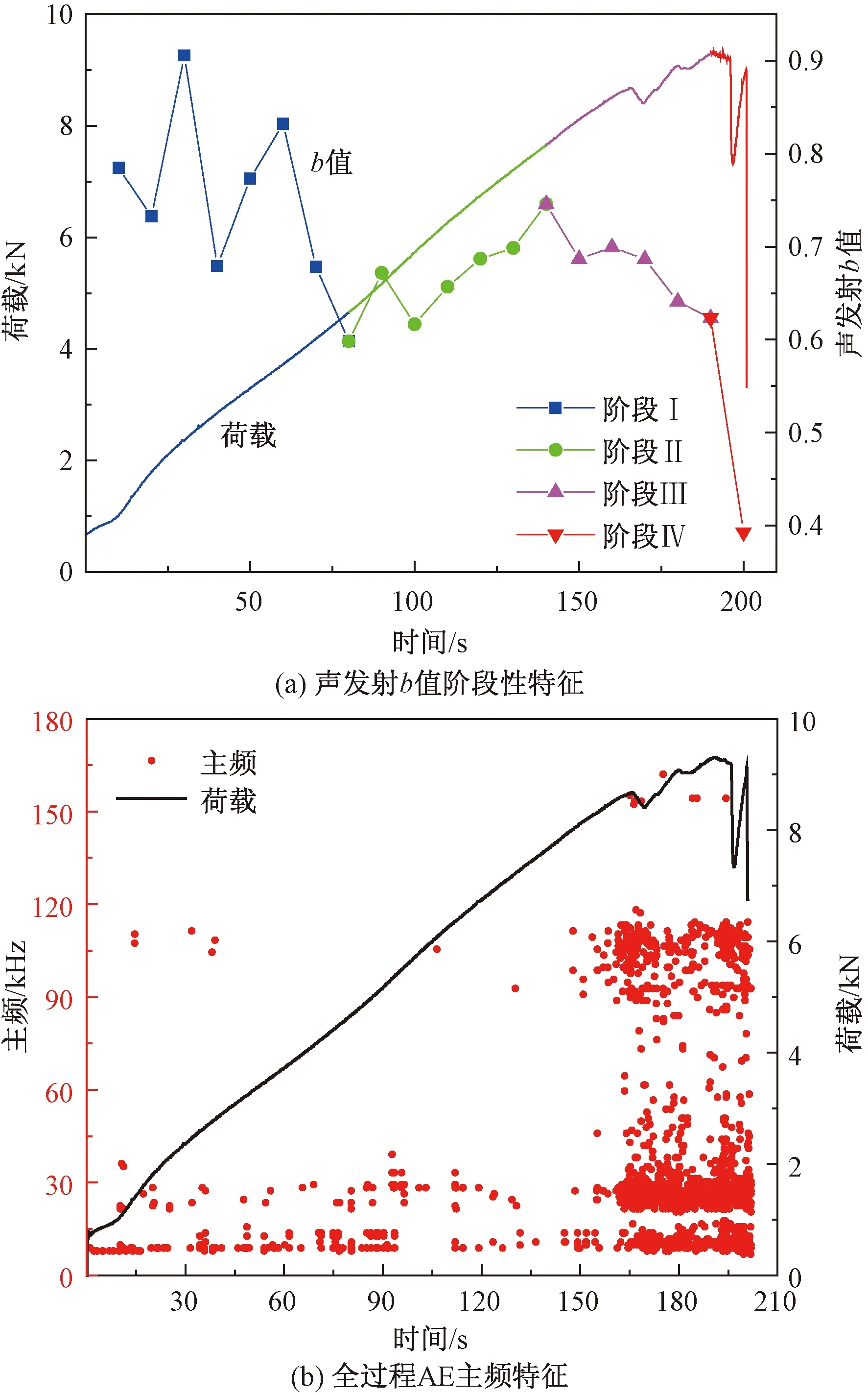
图6 试验过程特征统计分析Fig.6 Statistical analysis of test process characteristics

(1)阶段Ⅰ：微裂隙闭合(0～80 s)。加载初期，产生的声发射事件较少，单个声发射事件能产生较强的影响因子导致b值的浮动较大。锁固段的剪应力缓慢增加，存在与荷载成一定角度的微裂隙闭合，由荷载作用下颗粒之间的相互摩擦造成的。

(2)阶段Ⅱ：微裂纹萌生、发展(80～140 s)。b值呈持续上升，表明锁固段内部小尺度微破裂事件为主导特征，处于弹性变形阶段。

(3)阶段Ⅲ：宏观裂纹萌生、发展(140～190 s)。b值呈连续下降的趋势，在上部荷载剪压作用下锁固段内部大尺度的微破裂事件不断增加，表明由微裂纹为主到少量宏观裂纹为主的过程转变，通过模型加载过程的照相监控，在180 s监测到了明显的宏观裂纹[图7(c)]，与AE监测结果[图6(b)]吻合。

(4)阶段Ⅳ：宏观裂纹贯通、破坏(190～200 s)。b值急剧下降，大尺度微破裂事件急剧增加，锁固段裂隙贯通并失去锁固能力[图7(d)]，能量完全释放。

图7 锁固段裂纹扩展模式阶段性特征Fig.7 Stage characteristics of crack propagation mode in locking section

2.1.2 变形破坏全过程声发射主频特征及演化

通过快速傅里叶变换(fast Fourier transform,FFT)对锁固段物理模型加载全过程声发射信号进行频谱分析，图6(b)为AE主频特征随时间的演化规律，横坐标是时间，纵坐标是荷载与主要频率。研究发现，在锁固段微裂隙闭合阶段(阶段Ⅰ)，裂纹扩展不明显，主频主要分布在0～40 kHz。阶段Ⅱ随着微裂纹萌生、发展，声发射事件越来越密集。阶段Ⅲ、阶段Ⅳ密集出现了100、120、160 kHz的高频声发射信号。

2.1.3 变形破坏全过程声发射幅度特征及演化

图8为锁固段滑坡物理模型加载过程中的AE主频-振幅特性，不同阶段的主频-振幅分布特征差异很大，明显看出图8中有2个或3个主频带。为了分析幅度和主频的分布特征，结合声发射主频时空演化特征[图6(b)]采用一种统计方法[27]将AE信号分为低频带(20～40 kHz)、中频带(40～80 kHz)和高频带(80～180 kHz)3个频带，低于20 kHz为视为试样的自然背景频率，该信号主要由加载装置与模型接触部分的摩擦所产生。

图8 AE频率振幅阶段性分布特征Fig.8 AE frequency amplitude stage distribution characteristics

在加载过程中的阶段Ⅰ、阶段Ⅱ，AE信号主要分布在低频带且振幅较低；阶段Ⅲ AE信号主要分布在低频带和高频带两个主频带；第IV阶段AE信号幅值急剧上升，低频带尤为明显。总体上看低频信号数量多于高频信号的数量，低频信号振幅大于高频信号的振幅。高频信号随着宏观裂纹的萌生、发展开始出现，在阶段IV低频信号的幅值剧烈增长，可作为锁固段临滑失稳的前兆判识依据。

2.2 锁固段变形破坏应变特征及演化

通过工业相机对模型加载全过程锁固段区域的图像进行了密集采集，采用DIC对采集图像进行深入分析。图7为模型在加载过程中从初始状态到最终破坏4个阶段的代表性数字图像及裂纹分布实况(以40、110、180、195 s为例)，模型前缘在荷载的作用下产生蠕变，后缘裂隙增大并在锁固段部分产生应力的集中，引起锁固段两端产生拉裂破坏[图7(c)所示]，随后张拉裂纹的发育产生锁固段的体积膨胀，为旋转剪切破坏产生提供空间条件[图7(d)]。随后，通过DIC分析了模型加载变形破坏全过程的数字图像，获得模型表面精细化的位移、应变演化规律，如图9、图10所示。与图7一致，取40、110、180、195 s为4个阶段代表性特征点。

阶段Ⅰ：由于材料的弹性性能，锁固段位移场显示均匀，最大位移不超过0.03 mm，如图9(a)、图9(e)所示。水平方向的应变场呈无规则的细微变化，蠕滑段出现了较小的竖向应变(力)集中累积，如图10(a)所示。

阶段Ⅱ：锁固段位移场出现明显的分区[图9(b)、图9(f)]，蠕滑段尾端有向上的水平方向应变累积[图10(b)]，在滑移提供的驱动力下微裂纹开始萌生和发展，出现在预制裂隙尖端附近。

阶段Ⅲ：预制裂隙内尖端成核沿近垂直方向形成两条张拉裂隙[图7(c)]，与水平位移场相对应[图9(c)]。在应变场的拉伸裂纹轨迹处观测到应变集中[图10(c)、图10(g)]，对应宏观裂隙的萌生与发展。

图9 基于DIC的锁固段位移场阶段演化特征Fig.9 Phase evolution characteristics of displacement field in locking section based on DIC

阶段Ⅳ：随着荷载的持续增加，锁固段中部出现由左右两侧挤压形成的剪切裂隙，锁固段失稳破坏[图10(d)、图10(h)]与图7(d)相吻合。

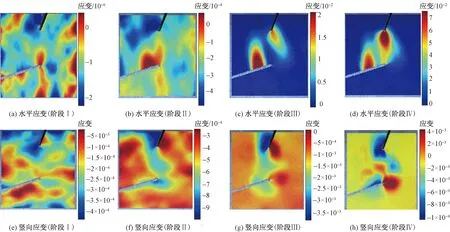
图10 基于DIC的锁固段应变场阶段演化特征Fig.10 Phase evolution characteristics of strain field in locking section based on DIC

DIC技术提供了一种非接触式的测量方法，对锁固段区域的微应变及裂隙发展演化趋势进行直观的识别。通过应变的集中分布，查明微裂纹最初萌生于预制裂隙尖端，并沿近垂直方向扩展，在拉应力的作用下微裂隙发展演化成为宏观拉伸裂纹，锁固段中部在剪压力作用下形成切应力，锁固段贯通破坏意味着锁固能力的最终失效。DIC测量结果与声发射特征演化规律相互印证、吻合。

2.3 破裂模式及动态演化

GMM是一种无监督的学习算法，表示在总体分布中含有k个遵从高斯分布的子分布的概率模型，即观测数据在总体中的概率分布[15]。

图11(a)、图11(c)、图11(e)及图11(g)为声发射特征参数GMM聚类分析结果，将所有声发射事件分为两类，对应模型剪切破裂和拉伸破裂两种模式，每个数据点将获得与该类相对应的唯一标记(标签)。随后，SVM通过使用GMM得到的样本数据以及特征向量来计算分类超平面[图11(b)、图11(d)、图11(f)、图11(h)]，即量化两种破裂模式的分界线。为提高SVM模型的鲁棒性和泛化能力，将数据集分为训练集和测试集，随机挑选样本得20%作为测试集。

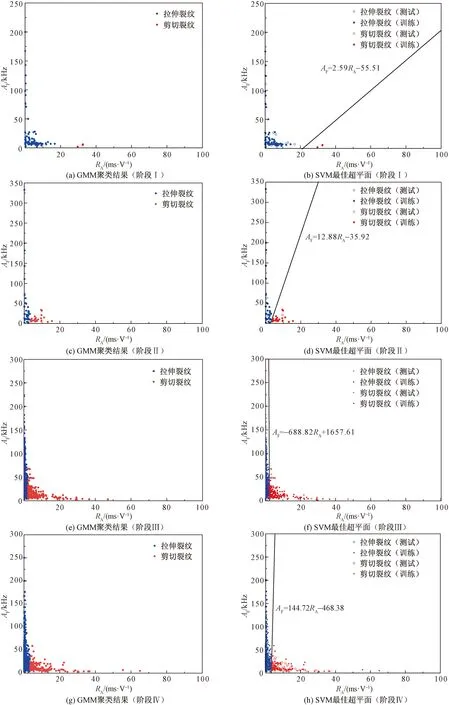
图11 基于GMM的聚类结果及SVM发现的最佳超平面Fig.11 GMM-based clustering results and the best hyperplane discovered by SVM

由分析结果可知，在阶段Ⅰ、阶段ⅡRA值较小(0～30 ms/V)，且主要集中在0～20 ms/V，锁固段内部没有或者少有剪切破裂的出现。由GMM聚类结果可知，阶段Ⅱ剪切裂纹的数量明显多于阶段Ⅰ。阶段Ⅰ中SVM计算的最佳超平面为AF=2.59RA-55.51，斜率小于阶段Ⅱ的12.88，表明剪切破裂事件在前期呈增长趋势。随着加载的进行逐渐出现高RA和低AF值特征的声发射信号，阶段Ⅲ高RA值(20～50 ms/V)声发射数量明显的增加，且剪切裂纹的数量剧烈增长，破裂模式呈现由拉伸破坏到拉伸与剪切的混合破坏的时空演化，由SVM计算的最佳超平面为AF=-688.82RA+1 657.61。阶段Ⅳ出现40～70 ms/V的高RA值的声发射事件，其剪切裂纹与拉伸裂纹声信号数量分布相似。综上，锁固段的破坏过程伴随拉伸破坏与剪切破坏，先以拉伸破裂为主，逐步过渡到剪切破坏为主，并伴随大尺度微破裂事件发生，最终导致锁固段宏观破坏和整体失稳。

3 结论

开展了单轴静力加载条件下“三段式”锁固段破坏模型试验研究。得出如下结论。

(1)锁固段孕育破坏过程的声发射特征具有明显的阶段性。根据声发射b值特征将锁固段破坏分为微裂隙闭合，微裂纹萌生、发展，宏观裂纹萌生、发展，宏观裂纹贯通、破坏4个阶段。

(2)对锁固段微应变的光学测量可以定量查明锁固段破裂损伤的演化规律。基于应变场的演化规律，微裂纹最初萌生于锁固段两端，并沿近垂直方向扩展成核，在滑移提供的驱动力下演化成为宏观拉伸裂纹，最终形成锁固段压剪破坏，可将视为锁固段即将失稳的前兆预警。

(3)建立了基于声发射特征与GMM-SVM机器学习的锁固段滑坡破裂模式分类方法。锁固段的破坏过程伴随拉伸破坏与剪切破坏，拉伸破坏存在破裂的整个过程，而剪切破坏存在加载后期，伴随着高RA值(40～70 ms/v)声发射事件的出现，由大尺度的微破裂事件引起。