具有Lévy飞行和反向学习的增强型人工蜂群算法

李 星，张少平，邵 鹏

(江西农业大学计算机与信息工程学院，南昌 330045)

群体智能的概念源于社会性昆虫的群体行为研究，随着蚁群优化算法和粒子群优化算法的提出，群体智能算法方面的研究开始广受关注。群体智能优化算法是种基于概率的随机搜索进化方法，其主要是模拟昆虫、鱼群、鸟群和兽群的自组织性群体行为，因此也属于生物启发式算法。其中，觅食是群体行为中最为关键的生存行为，也是群体智能算法经常模仿的群体行为之一。在觅食过程中，个体之间以某种方式分享信息，从而能够在短时间内快速得到更多的食物，这种群体行为抽象出的算法称为群体智能算法[1]。

人工蜂群算法(artificial bee colony,ABC)是群体智能算法之一，而且已证明ABC算法的性能与其他基于群体的算法相比具有竞争力[2-4]。ABC算法模拟蜜蜂的觅食行为，该算法设计的最初目的是解决多变量函数优化问题。ABC算法具有收敛速度快、控制参数少、操作简单和易于实现等特点，因此在处理有约束的实际问题上表现出了其优势。近年来，经过不断的研究与延伸，ABC算法的运用也越来越广泛，如图像处理[5]、电力系统[6-7]、数据挖掘[8]、工程应用[9]和组合优化[10]等。然而，该算法也有其自身的局限性，如容易陷入局部最优等。

为了更好地运用ABC算法解决实际问题，众多学者致力于标准算法的优化工作，因此不断有优秀的ABC算法变体涌现出来。就目前而言，改进算法的方法主要体现在初始化种群的改进、搜索策略的优化以及算法的混合等方面。

文献[11]受反向学习(opposition-based learning,OBL)机制的启发，在初始化种群和解的搜索过程中引入OBL，再通过自适应权重策略平衡算法的全局探索和局部开发能力，提出的改进ABC具有很好的收敛速度和优化精度；文献[12]将自适应DE算法与精英OBL相结合，克服了算法后期多样性下降的缺点；文献[13]通过增加全局最优个体信息的利用，达到改善搜索效率的目的，提出了全局最优(global best,Gbest)指导的人工蜂群算法；文献[14]在人工蜂群算法的基本框架下结合新的搜索策略和概率模型，以提高好解的选择概率；文献[15]提出了一种新的具有智能学习策略和湍流算子的ABC算法，不仅提高了向更好的个体学习的机会，还定义了一种新的方向机制克服搜索过程中的振荡现象；文献[16]为使小区等待时间和自动导引车总行驶距离的标准差最小，采用包括基于启发式的初始化、六邻域结构和新的进化策略技术，提出一种有效的离散人工蜂群算法；文献[17]将Lévy飞行结合多目标蜂群算法，以解决无线传感器网络中的部署问题；文献[18]根据Lévy飞行具有短步长和偶尔长步跳跃的特征，向粒子的更新公式引入Lévy飞行策略来提高种群的多样性；文献[19]提出一种能够使用概率因子p动态确定蜂群大小的动态ABC算法，并运用于发电系统中的环境经济调度问题；文献[20]用Boltzmann选择机制取代标准ABC中的轮盘赌策略，提出一种用于优化多变量函数的改进算法；文献[21]将极值优化(extreme optimization,EO)和Boltzmann选择概率引入在前期工作，新提出两个ABC改进版本，并将它们应用于光伏模型的两种参数识别问题；文献[22]结合一种新颖的自适应修改率自适应地平衡ABC算法中的探索和开发过程；文献[23]将几种不同性质的搜索方程与传统ABC算法结合，提出多策略集成的人工蜂群算法；文献[24]通过混合人工蜂群和蚁群优化算法，实现虚拟机在主机间的负载均衡；文献[25]引用差分进化(differential evolution，DE)算法中的变异和交叉运算，设计出具有新的二进制搜索算子的二进制ABC算法，用于解决0～1背包问题；文献[26]中ABC可以根据最小距离和数据传输次数，找到数据副本最佳放置的解决方案，并利用背包方法和数据复制的可用性降低成本；文献[27]采用反向人工蜂群算法(opposition artificial bee colony，OABC)重建人工神经网络，以配置最佳数目的隐藏层及其相关的神经元；文献[28]将人工蜂群算法训练的多个神经模糊滤波器与决策树算法相结合，用于消除SAP(salt and pepper)噪声，其使用基于回归的神经模糊网络来处理高度损坏的灰度和彩色图像。

从上述研究发现，OBL和Lévy飞行策略对算法改进有着很好的效果，如能够避免早熟、加速收敛和提高优化精度等，但关于ABC算法与该两种策略的研究尚鲜见报道。文献[29]提出了一种基于反向学习的Lévy飞行人工蜂群算法，该算法中增加Gbest个体指导雇佣蜂和观察蜂阶段的邻域搜索过程，并引用两个自适应参数决定是否启动反向学习和Lévy飞行机制。区别于该算法，将通过新的改进方式结合上述两种有效的策略，提出一种具有Lévy飞行和反向学习策略的增强型人工蜂群算法，以进一步提高算法的性能。

1 相关工作简述

1.1 人工蜂群算法

在ABC算法中，可以将整个蜂群分为雇佣蜂(employed bees)和非雇佣蜂两大类。其中，非雇佣蜂中又包括观察蜂(onlooker bees)和侦查蜂(scout bees)两种。在觅食过程中，3种蜜蜂有明确的分工但又相互配合，因此蜜蜂之间存在着角色转换。雇佣蜂负责搜索食物源，且食物源与雇佣蜂之间存在一一对应的关系。雇佣蜂完成全部的食物源搜索后，再将食物源信息分享给观察蜂。雇佣蜂的数量与观察蜂相等，分别占种群数量的1/2。食物源信息中包含方向、距离、丰富度和开采的难易程度等内容。观察蜂先根据雇佣蜂提供的信息判断食物源的优劣，再决定是否跟随雇佣蜂开采该食物源。当某食物源出现枯竭时，该处的蜜蜂将会放弃此食物源，并且在此时转变为侦查蜂开始寻找新的食物源，确保不会出现食物源短缺的现象。找到食物源后，侦查蜂又转变为雇佣蜂。

食物源对应于优化问题中的候选解，候选解的优劣由食物源的适应度值衡量。食物源的适应度值越好，候选解越接近目标解，即候选解越好。求解优化问题时，ABC算法主要通过选择和变异寻找最优解，以此驱动整个种群更新。选择过程确保能够利用之前的经验，通过不断进行贪婪选择，逐渐接近问题的最优解。变异过程允许探索解空间中的未知区域，在搜索空间内生成新的候选解位置，实现候选解的更新。ABC算法各阶段具体步骤如下。

步骤1初始化阶段。在该阶段，初始化所需参数，随机生成初始食物源位置(初始解)。初始化的参数有种群数量SN、最大迭代次数MaxCycle、控制参数Limit、搜索维度D以及搜索边界等，初始解Xi=(xi1,xi2,…,xiD)通过式(1)生成。

xij=xminj+rand(xmaxj-xminj)

(1)

式(1)中：i=1,2,…,N解的个数N为种群数量SN的1/2；j=1,2,…,D；下标maxj为第j维搜索空间上解的上限；下标minj为下限；rand为产生[0，1]均匀分布的随机数。

利用式(2)计算食物源Xi的质量，即适应度值。

(2)

式(2)中：f(Xi)为食物源Xi对应的目标函数值；fit(Xi)为食物源Xi的适应度值。

步骤2雇佣蜂阶段。在该阶段，雇佣蜂对所有的食物源周围进行搜索。只要搜索次数小于Limit的预定值，循环选择质量更好的食物源进行保留，即贪婪选择过程。式(3)为邻域搜索的方程，在食物源Xi周围搜索得到新的食物源Vi=(vi1,vi2,…,viD)。

vij=xij+φij(xij-xkj)

(3)

式(3)中：φij为[-1，1]服从正态分布的随机数，控制邻域内食物源产生的范围；k∈{1,2,…,N}，k≠i，即Xk不同于Xi。

由式(3)可以看出，ABC算法自身具有自适应的收敛性。随着Xi和Xk之间的差值越来越小，新食物源的位置变化也不断减小，进行循环搜索后不断靠近最优解[30]。

步骤3观察蜂阶段。在该阶段，雇佣蜂已完成对所有食物源的搜索工作，将以摇摆舞的方式传递记录的食物源信息给蜂巢中等待的观察蜂。观察蜂需要根据式(4)计算每个食物源的选择概率P(Xi)，由于观察蜂以轮盘赌的方式选择食物源，所以质量好的食物源被选择的概率更大。

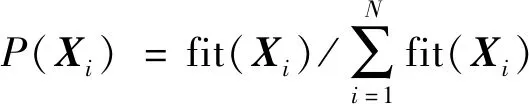
(4)

当P(Xi)大于[0，1]内产生的随机数时，按照式(3)再次对食物源Xi进行邻域搜索，然后对候选食物源进行贪婪选择。

步骤4侦查蜂阶段。在该阶段，经过Limit次循环依然没有更新的食物源将被舍弃，因为该食物源已经是当前邻域内可以得到的最好食物源，即算法可能陷入了局部最优无法跳出。该处蜜蜂转变为侦查蜂，并按照式(1)重新寻找食物源。当找到新食物源后，侦查蜂又重新转换为雇佣蜂继续搜索过程。

1.2 Lévy飞行

在自然界中，大多数动物都通过短距离和长距离相结合的搜索方式寻找未知环境下的食物。曾有研究表明，对分工合作的觅食者来说，最理想的寻找食物的路线就是Lévy飞行的轨迹，也在许多动物和昆虫的觅食行为中发现了Lévy飞行的重要特性[31]。作为随机游走过程，Lévy飞行包括大多数个体短距离局部搜索和少数个体远距离全局探索，而且搜索方向也会发生变化，这有助于算法跳出局部最优。因此，优化和搜索领域通常利用Lévy飞行扩大搜索空间和增强全局搜索能力。

随机游走过程中，步长的概率分布是重尾分布，偶尔会有大跨步，即可能导致生成的解在边界之外，因此使用Lévy策略时需要合理控制步长的大小。Lévy分布如式(5)所示，通常使用Mantegna方法计算Lévy分布。

Lévy～u=t-β， 1≤β≤3

(5)

式(5)中：u和t为服从正态分布的参数；变量β为[1,3]区间内的数。

1.3 反向学习

在标准ABC算法中，当随机化的初始解接近全局最优时，找到目标解需要的计算成本较小。但当初始解离最优解很远时，计算成本往往很高，有时甚至是不可行的。根据Tizhoosh[32]提出的反向学习的概念，同时考虑候选解及其对应的反向解，可以提高算法的搜索效率，从而减小计算成本。研究表明，对于没有先验知识的优化问题，反向解比随机解到达全局最优的概率更高。在概率论的基础上，反向解有一半的概率更接近最优解。

2 增强型ABC算法设计

对于ABC算法存在探索开采间不平衡、相似个体聚集，以及找到局部最优后无法快速靠近全局最优的不足。利用当前最优解的信息结合Lévy飞行和反向学习策略提出ELOABC算法，加速算法收敛、一定程度上避免算法早熟，弥补了标准算法的不足。

2.1 增强型ABC算法中的Lévy飞行设计

增强型算法保留了原算法的邻域搜索过程，对邻域搜索得到的解按照式(6)生成Lévy解Li=(li1,li2,…,liD)，再贪婪选择保留最好的解。

lij=vij+α(vij-xkj)Levy(β)

(6)

式(6)中：α为步长缩放因子，取α=0.001；Levy(β)为Lévy飞行生成的值，β=1.5。

利用局部搜索得到的解的信息，加以Lévy飞行长短步长结合的尝试，一定程度上避免了算法陷入局部最优。

2.2 增强型ABC算法中的反向学习设计

xnewj=xbestj+rand(xij-xbestj)

(7)

式(7)中：xbestj为当前种群中的最优解。

通过利用当前最优解的信息，再结合反向学习策略更新种群，该阶段可以提高算法的收敛速度和跳出局部最优的能力。

2.3 增强型ABC算法描述

ELOABC算法的具体流程如表1所示。

表1 ELOABC算法Table 1 Algorithm of ELOABC

3 实验仿真与分析

3.1 实验仿真

为了验证增强型算法的性能，采用15个经典测试函数对算法进行实验，并将所提出的增强型双策略人工蜂群算法与基于反向学习的单策略人工蜂群算法(opposition-based artificial bee colony algorithm,OBLABC)和标准ABC算法分析比较。

测试实验中，F1～F13是群智能算法中常使用的经典函数，函数F14和F15选自CEC 2005实参数优化特别会议，具有移位的特性。将这些基准函数分为四组，并在表2中列出了这些测试函数的类型、名称、搜索范围和理论最优值。第一组包含7个单峰函数，有简单的单峰函数F1～F4；不连续阶跃函数F5；当问题维度D=2、3时，F6是单峰的，但当维数很高时可能会变成多峰；有噪声的四次函数F7。这些单峰函数可用于测试算法的收敛速度。第二组包括6个多峰函数F8～F13，可以通过这些函数测试算法的全局搜索能力，其局部最优的数量随问题维度呈指数增长。第三组是移位的单峰函数F14，最后一组是移位的多峰函数F15,移位函数要复杂得多，这使得测试组更加全面和有说服力。

表2 测试函数描述Table 2 Description of benchmark functions

为保证公平比较算法性能，参照相关资料统一设置实验参数。其中，雇佣蜂和观察蜂的数量相等，是种群总数量的1/2。为避免偶然性误差，所有算法在每个测试函数上执行25次，实验所设置的具体数据如表3所示。记录实验所得最优值、最差值、平均值和标准差作为算法的性能评价指标，3种算法的测试结果如表4所示。

表3 实验参数设置Table 3 Experimental parameter settings

表4 3种算法优化结果比较Table 4 Comparison of optimization results of 3 algorithms

为了更直观地对比3种算法收敛性能，如图1所示，选取了除Step函数(标准算法也找到最优值)外的14个测试函数，绘制了ABC算法、OBLABC算法和ELOABC算法的求解进化曲线。在纵坐标名称中，log表示取函数优化值的自然对数。由于存在两组数据有时相差较近，迭代次数较大时无法清晰显示差别，部分曲线只截取前30 000次迭代数据的变化。

图1 3种算法收敛曲线Fig.1 Convergence curves of three algorithms

3.2 结果分析

平均值能较大程度地降低偶然误差的影响，因此将其作为三种算法的主要评价指标。如表4所示，加粗的平均值最接近理论值，表示该算法的优化效果越好。由表4可知，对于F1、F2、F3、F4、F5、F9和F10，OBLABC算法和ELOABC算法都找到了它们的理论最优值，其中F5在标准ABC算法下也找到了最优值0。由于F5中3条曲线基本重叠，因此图1没有给出该函数的求解进化曲线，可以看出，ELOABC在大多数情况下收敛速度优于OBLABC。在F12中ELOABC和原算法也找到了最优值，根据表4中标准差和图1(k)中曲线变化趋势可知，ELOABC性能更好些。在实验结果保留两位小数的情况下，表4中3种算法在函数F11所得数据除标准差外都相同，但结合曲线图1(j)发现原算法在该函数的求解精度要差些。此外，对于F6、F12、F13、F14和F15，OBLABC算法表现不佳，各项指标与标准算法相差甚远，而在OBLABC算法上引入Lévy飞行的ELOABC算法较好的克服了这点，明显改进了寻优性能。对于F7，虽然没有找到理论最优值，但OBLABC算法和ELOABC算法相较于原算法寻优结果也有明显改善。F8是十分复杂的非线性全局优化函数，在该函数上寻优改进效果较弱，ELOABC依然比OBLABC表现出更好的算法性能。

综上所述，结合表4中数据和图1中变化曲线，随着迭代次数的增加，ELOABC在收敛速度和寻优精度上性能都有所提高。虽然ABC和OBLABC算法的部分收敛曲线和ELOABC算法很接近，但整体来说ELOABC得到的函数求解结果更好。因此，ELOABC算法在稳定性方面表现更好，增强了算法的寻优性能。

为更好地验证上述结论，如表5所示，介绍了Friedman检验和Wilcoxon检验的统计结果。在检验中，算法排名值越低排名顺序越高，显著性水平(P值)低于0.05表示该算法明显优于对比算法。由此可知，3种算法的性能排名为：ELOABC、OBLABC和ABC，即ELOABC算法取得最高平均排名。根据所得P值可知，ELOABC明显优于OBLABC算法和ABC算法。

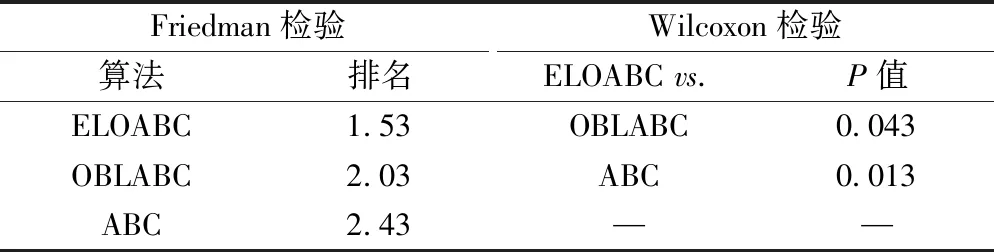
表5 检验统计结果Table 5 Test statistical results

4 结论

在处理优化问题时，人工蜂群算法表现出其优势，但仍然存在容易陷入局部最优、后期收敛速度慢、精度不高的缺点。为了进一步提高ABC算法的性能，引入Lévy飞行和反向学习两种性能优秀的策略，提出一种具有Lévy飞行和反向学习的增强型人工蜂群算法。该算法利用反向学习策略加速算法求解、增强跳出局部最优的能力，同时结合Lévy飞行有助于加强优化效果。通过15个基准函数对改进算法的性能进行了测试，由实验结果分析可知，增强型算法提高了原算法的收敛速度、寻优精度和全局寻优能力，这意味着所引入的两种策略在提高人工蜂群算法的优化性能上起着重要的作用。