载重轮胎的轮印载荷分布特性试验研究

何市伟，刘晖，张梗林，王德禹*

1 上海交通大学 海洋工程国家重点实验室，上海 200240

2 上海交通大学 海洋装备研究院，上海 200240

3 中国船舶及海洋工程设计研究院，上海 200011

0 引 言

轮印载荷是船舶结构常见的载荷类型，其载荷分布规律会影响结构的应力分布情况，进而影响船舶结构的可靠性。轮印载荷的特点是作用位置不固定，且具有载荷局部集中的现象，这对船舶结构有较高的设计要求。但在进行船舶设计工作时一般将轮印载荷近似为矩形均布载荷[1]，客观上忽视了轮印载荷的实际分布特性，可能使得板材强度利用不充分或对强度估计不足。因此，探究轮印载荷的分布特性对于船舶设计工作具有重要意义。

国内外许多学者已经对轮印载荷进行了大量的研究工作，如Jackson等[2]通过局部载荷测试单元和真实轮胎加载的方式模拟加筋板结构的实际受载情况，研究了轮印载荷的分布规律和相应的甲板设计方法。但没有分析具体的轮印压力分布特性，只是将其视为条状载荷加以应用。Wesołowski等[3]研究了带有纵沟花纹的飞机轮胎与机场路面相互作用时接触压力的分布规律，给出了轮胎接地面积和胎内气压等变量之间的关系，在研究过程中忽略了轮胎花纹的影响。Zhu等[4]以橡胶块代替轮胎进行了加筋板强度试验，进而研究了在重型车辆及直升机轮载作用下加筋板结构的极限承载能力和塑性变形规律，并提出了加筋板板厚的弹塑性设计方法。王智慧[5]以橡胶块代替轮胎进行了轮印载荷分配试验，得到了轮印载荷的单峰分布特征，然后结合数值仿真模型对橡胶厚度和硬度、加筋板和波纹板几何参数以及轮印大小的影响进行了研究。Zhu等[4]和王智慧[5]都以橡胶块代替轮胎进行了轮印载荷的研究工作，但忽略了轮胎与橡胶块载荷分布情况的差异。刘聪等[6]采用橡胶块模拟轮印载荷，研究了加筋板上的应变分布规律及轮印载荷等效方法，并考虑了初始缺陷等因素的影响，试验结果显示，接触压力呈现单峰分布形式。胡小弟等[7]通过自研的静态压力测量装置，对重型货车轮胎的接地压力分布特性进行了大量试验测定，研究结果表明重载下的轮印形状接近于矩形，接触压力分布情况与轮胎气压和载荷有密切关系。柳帅蒙[8]采用有限元法模拟了重型货车载重轮胎的接地压力分布情况，认为接地压力分布形式整体呈马鞍形，并将一元复指数函数和双指数函数相结合，给出了马鞍形接地压力分布规律的数学表达形式。Mohsenimanesh等[9]通过轮胎泥土试验的方法测定了充气轮胎在泥土中的压力分布情况，研究了充气压力对轮印面积、轮辙深度和压力分布的影响。Polasik等[10]通过试验测定了作用于路面的轮胎轮印形状、轮印面积与轮胎气压之间的关系，并介绍了一种测量接触面积的方法。Sebastian等[11]研究了轮印载荷与均布位移载荷作用于相同夹层板结构时的差异，结果表明两者一般分布规律的区别十分显著，还讨论了加载过程中介质的影响及加载方式的影响。

以上研究对于轮印载荷分布规律的探究及简化具有重要指导意义。而加筋板是船舶的典型结构和基本结构，对加筋板轮印载荷分布特性的研究工作比较缺乏。且设计船舶相关结构时通常将轮印载荷视为均布载荷，忽略了轮印载荷的不均匀性，这可能导致难以准确评估轮印载荷作用下加筋板结构的安全性能。为此，本文将通过加筋板轮压试验，得到载重轮胎在加筋板结构上的载荷分布特性，这对于加筋板在轮印载荷作用下的安全性评估有重要意义。

1 试验方案

1.1 试验模型

为确定轮印载荷在加筋板上的分布特性，本文设计了如图1所示的试验模型，图中U表示位移计测点位置（与5号应变测点相邻），模型材料为铝合金。模型的长度为1 600 mm，宽度为1 400 mm，纵骨间距为200 mm，纵骨跨距为600和400 mm。强横梁高度为200 mm，其带板宽度为100 mm。为了模拟固支边界条件，在模型四周增设了厚度为20 mm的带孔围板，以此与四周工装件栓接。

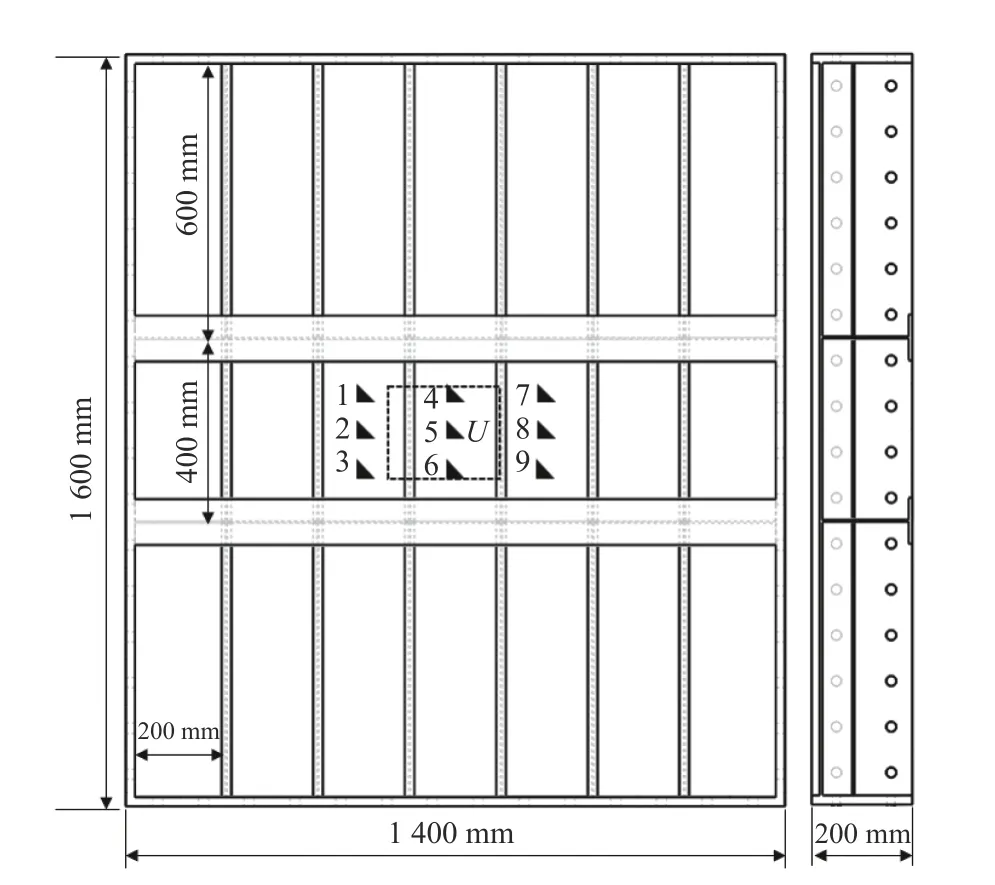
图1 模型结构示意图Fig.1 Schematic diagram of model structure

1.2 试验工况

本次试验共4个工况，加载位置如图1中虚线框表示，轮胎前进方向与加筋板纵骨平行。载重轮胎负荷能力为5 050 kg，充气压力为0.95 MPa，胎冠宽度270 mm，各工况参数如表1所示。

表1 工况表Table1 Load cases

1.3 测点布置

本次试验需要获取模型应变位移、轮印形状和接触压力等数据。模型面板上共布置了9个三向应变测点，布置情况如图1所示。板格内在加载区布置1个位移测点，紧靠5号应变测点位置，如图1中U所示，通过位移计来测量加筋板垂向位移，所用位移计为千分尺，量程100 mm，其布置情况如图1所示。试验通过压力膜片测量接触压力，在轮胎表面共布置了8个压力测点，由于轮胎花纹的影响，测点布置如图2所示。根据载重轮胎花纹的分布情况，以获取接触位置的轮胎表面的压力分布。此外，试验过程中还测量了不同载荷工况下的轮印形状和面积。

图2 压力测点和位移计布置Fig.2 Layout of pressure measuring points and displacement points

1.4 试验流程

试验装置如图3(a)所示，试验模型通过螺栓与工装框架联接，然后吊装至4个支撑座上，以螺栓固定。试验过程中使用加载油缸施加载荷，通过轮胎支架将载荷传递到载重轮胎。为了得到模型相对危险工况（区域应力达到极限状态时即为危险工况，相对危险工况即测点临近模型最危险区域）的数据，通过数值仿真计算确定了如图1虚线框所示的加载位置，试验中加载位置如图3(b)所示。试验之前首先进行预加载以保证轮胎与加筋板之间的充分接触，过程中载荷加载分级缓慢进行，最终达到预定载荷。

图3 试验结构总装和加载位置Fig.3 Experiment assembly and loading position

2 试验结果

2.1 材料拉伸结果

为了获得试验模型材料的应力–应变关系，本试验根据规范GB/T 228—2002《金属材料 室温拉伸试验方法》[12]要求定制了相应的拉伸试件并进行了单轴拉伸试验。材料应力–应变曲线如图4所示，其弹性模量为68 GPa，名义屈服应力为168 MPa，泊松比为0.33，所得到的材料应力–应变关系将用于数值仿真计算和校验。

图4 铝合金材料的应力–应变曲线Fig.4 Tensile curve of aluminum alloy material

2.2 轮印形式

在轮印采集过程中，首先在轮胎上均匀涂抹染色剂，并将采集纸放置在轮胎下方。载荷为2～5 t，加载后即可得到如图5所示相应载荷的轮胎印迹，图中红色线表示轮印近似轮廓。由图可见，随着载荷的增加，轮印形状由椭圆形转变为矩形，这与船舶设计过程中所考虑的矩形轮印非常相似。从图中可以看出，轮印宽度与轮胎宽度相同，仅长度有变化。以轮胎印迹的外轮廓作为轮印面积计算范围，花纹块部分占总面积S的比例λ（有效面积比）为64%左右。

为了便于设计，这里将轮印形状转化为矩形，如图6所示，转化过程中保持轮印宽度与面积不变。对于载荷为2 t的轮印，保持轮印宽度和面积不变，长度转化为0.133 m；对于载荷为3 t的轮印，保持其宽度和面积不变，长度转化为0.166 m；至于4和5 t载荷的轮印则不转化。然后考虑花纹面积比，将矩形轮印面积转化为有效矩形轮印面积，转化过程中保持长宽比不变，如图6的点划线所示。图中2B’为轮印宽度，2L’为轮印长度，2B为有效轮印宽度，2L为有效轮印长度，转化后的结果如表2所示。

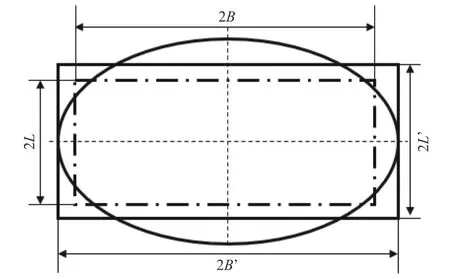
图6 轮印转化方法示意图Fig.6 Convert method of tire footprint

从表2可以看出，轮印面积随载荷大致呈线性变化，由于矩形宽度固定，轮印长度也呈线性变化，于是可以拟合出有效轮印长度2L与载荷W的关系，如式(1)所示。

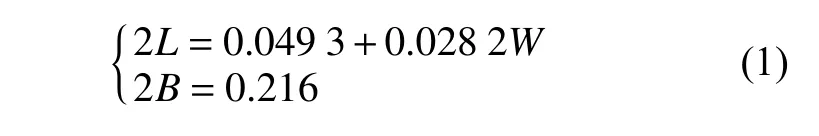
表2 轮印面积、尺寸与载荷的关系Table2 Relationship between tire footprint area, size and load

2.3 轮印压力

不同载荷下得到的压力数据在对称性方面存在一定误差。误差较大的原因分析如下：1）测点位置不对称以及轮胎花纹不对称可能导致结果存在差异；2）在载荷施加方面，轮胎加载时可能出现偏心现象；3）在轮胎结构方面，由于花纹块分布的影响，测点与花纹块边缘部位的距离可能影响压力值；4）在数据监测方面，有限的数据监测点和压力膜片的敏感性可能造成压力测点的数据出现不均匀现象；5）加筋板变形可能造成轮胎受载不均匀现象。在忽略上述误差的基础上，本文将部分试验测点数据根据对称性进行修正，测点1和测点6大致对称，测点2和测点7大致对称，测点3和测点5大致对称，分别取其平均值作为最终结果，试验数据如表3所示，修正结果如表4所示。

表3 不同载荷下各压力测点试验数据结果Table3 Testing results of each pressure point under different load cases

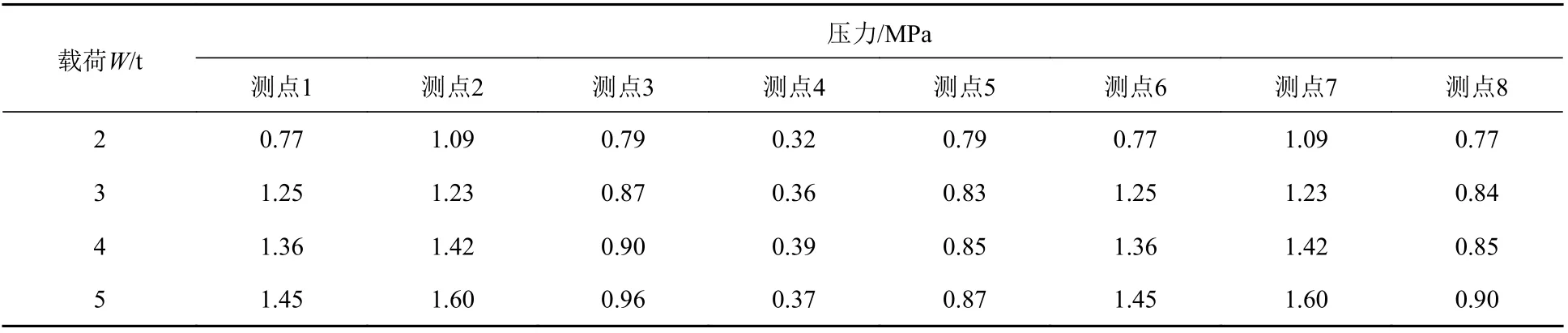
表4 不同载荷下各压力测点修正数据结果Table4 Modified results of each pressure point under different load cases

2.4 应力结果

试验中采用三向应变片对应的应力换算公式，即先通过应变片所测应变计算主应力，再通过主应力计算Mises应力。试验所得各测点应变数据转换为Mises应力的结果如表5所示。

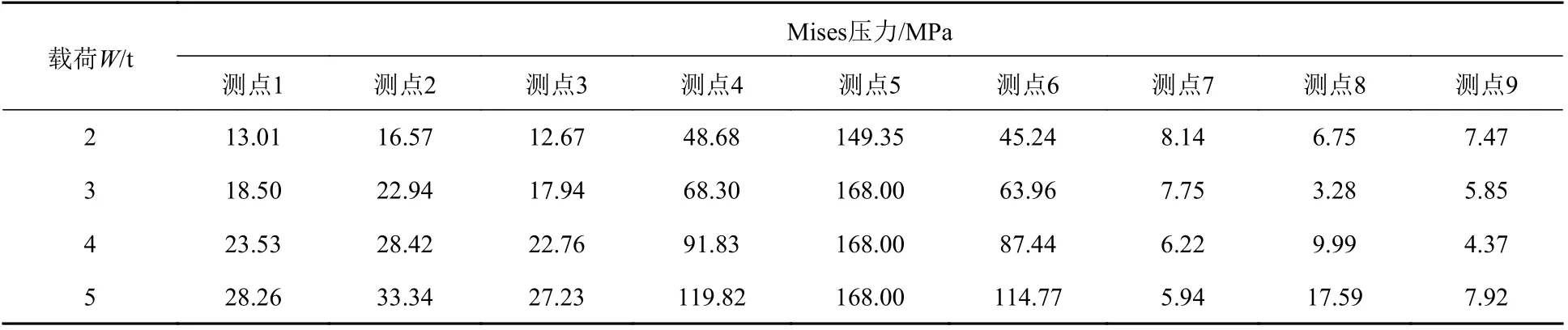
表5 不同载荷下各应变测点转换的Mises应力Table5 Mises stress of each strain point under different load cases

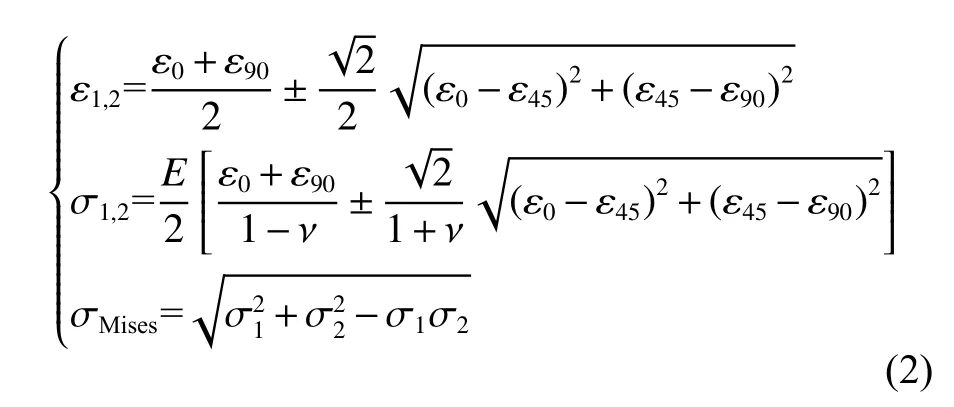
式 中： ε1,2为 面 内 主 应 变； σ1,2为 面 内 主 应 力；σMises为 Von Mises应力；ε0， ε45， ε90分别为三向应变片所测的3个方向应变；E为弹性模量；ν为泊松比。

由于在载荷达到3 t时测点5已经进入塑性阶段，应力和应变之间不再满足胡克定律，这里以名义屈服应力代替。除测点7，8，9外，其他测点依然处于弹性变形范围，对应的应力数据正常。对于测点7，8和9的数据，随着载荷增加，其应力出现持续下降或先降后升的现象。对此分析如下：根据表6所示试验应变数据，考虑到所有应变测点都布置在模型的下面板，可以判断这3个测点在加载初期处于受压状态；随着载荷的增加，逐渐变为受拉状态。这是因为，该测点所在板格与加载区域之间存在刚度相对较高的纵骨，一侧加载会使得另一侧面板相对翘起，即测点7，8，9所在板格出现下面板受压的情况；但随着载荷继续增加，纵骨具有一定的变形量，整个面板处于拉伸状态，即测点7，8，9所在板格下面板由受压逐渐变成受拉状态。而Mises应力为等效合成应力，不能反映应力拉压状态，因此应力出现异常变化。

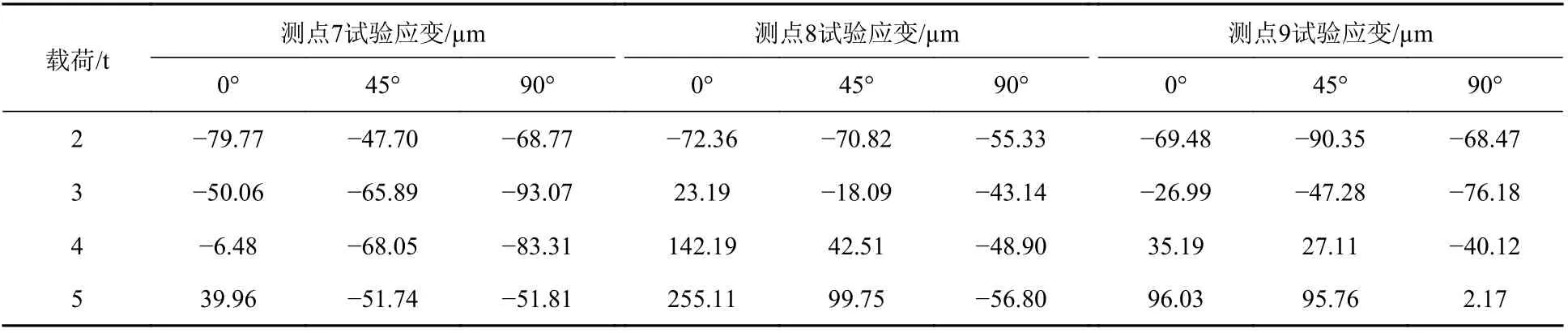
表6 不同载荷下测点7，8，9的试验应变Table6 Tested strain data of measuring points 7, 8, 9 under different load cases

2.5 位 移

位移测点主要监测板的垂向位移，在不同载荷下的试验结果如表7所示。

表7 不同载荷下位移测点结果Table7 Displacement results under different load cases

3 轮印载荷分布特性

3.1 轮印载荷分布形式

静止状态的轮胎接触压力分布形式受轮胎载荷、胎压、花纹以及路面物理特性等因素影响，但目前针对接触压力的研究大部分都忽略了轮胎花纹或仅考虑简单的纵向花纹。运动状态下轮胎的接触压力分布受滚动阻力影响在纵向上具有一定的非对称效应，且在胎宽方向上接触压力会向胎肩部位集中[13]。此外，路面的倾斜程度和轮胎转角等均会引起轮印载荷的不均匀分布现象[14]。本文仅考虑静态轮胎的压力分布特性，对于花纹的影响，则根据有效花纹面积比λ将轮印面积转化为有效轮印面积。

结合现有试验结果和相关文献[7-8,11,15-16]的成果可知，对于载重轮胎，当载荷小或胎压高时，接触压力在轮胎横向和纵向分布均表现为单峰值分布形式，这里称为Ⅰ型分布或凸型分布；随着载荷增加，接触区域压力分布呈现马鞍形，在轮胎横向或纵向之一出现双峰值，另一侧保持单峰值的分布形式，这里称为Ⅱ型分布或马鞍型分布；在载荷大或胎压低时，接触区域的压力在轮胎横向和纵向上都出现双峰值分布形式，这里称为Ⅲ型分布或凹型分布。为了简便有效地模拟轮印压力的分布情况，本文采用二阶多项式给出分布形式，且认为轮印的形状为矩形，如式（3）所示。

式中：p为轮印压力，MPa；x为横坐标，对应轮胎宽度方向，m；y为纵坐标，对应轮胎前进方向，m；a，b和c′为相应的系数，通过压力测点数据确定，坐标原点位于接触区域的中心处。

3种压力曲面示意图如图7所示，当a和b均为负值时，曲面呈凸型，与Ⅰ型分布情况相似；当ab＜0时，曲面呈马鞍形，与Ⅱ型分布情况类似；当a和b均为正值时，曲面呈凹型分布，与Ⅲ型分布情况类似。式（3）可以较好地反映轮印压力的分布形式。对于载重轮胎，在工作载荷范围内多是Ⅱ型或Ⅲ型分布的。此外，该分布形式不考虑轮胎滚动阻力扭矩和因侧倾等原因产生的压力分布不均匀现象。

图7 3种压力曲面示意图Fig.7 Schematic diagram of three pressure surfaces

轮印压力的分布情况由载荷与轮印面积决定，即载荷与压力分布对面积的积分存在确定关系，因此需要满足如下条件：

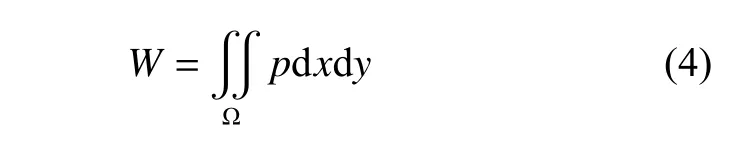
式中，Ω为轮印接触区域的边界。本文假设所得到的轮印都是紧密接触，不存在接触不充分情况。为了满足式（4），将式（3）中表示曲面高度的c′修正为c，修正后的表达式如式（5）所示。

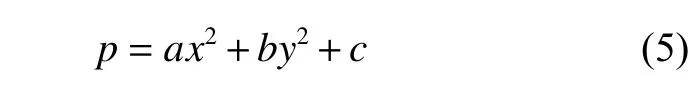
3.2 参数的确定

基于以上二阶多项式压力分布形式，其参数可由以下方法确定。本次试验结果如图8所示，首先取测点1，2，6，7的压力均值作为压力P1和P2，测点3，4，5，8的压力均值作为压力P0，结合轮印尺寸，即可确定相应的参数a，b和c′，其中参数a和b决 定了压力面形状，c′决定了压力面高度；其次，在满足式（4）要求的情况下将c′值修正为c。如5 t载荷时，测点1，2，6，7的平均压力为1.53 MPa，位置坐标取P1（0.108,0）和P2（0,0.096），测点3，4，5，8平均压力为0.77 MPa，位置坐标取P0（0,0），结合式（4）和轮印有效面积即可得到该载荷对应的参数，对应的曲面如图9所示。本试验对应的各载荷参数如表8所示，对应的压力试验值和计算值及其误差分析结果如表9所示。表9中平均误差指压力曲面与试验压力值的平均误差，其最大平均误差为15.7%；除4号测点外，大多数压力误差小于20%或在其附近，造成测点4数据误差的原因可能是轮胎花纹块中心区域与边缘区域载荷分布偏差。引起误差的因素也包括测点位置有偏差、样本点较少等。

表8 各载荷对应参数Table8 Parameters for each load case

表9 不同载荷下压力误差分析Table9 Error analysis of pressure under different load cases

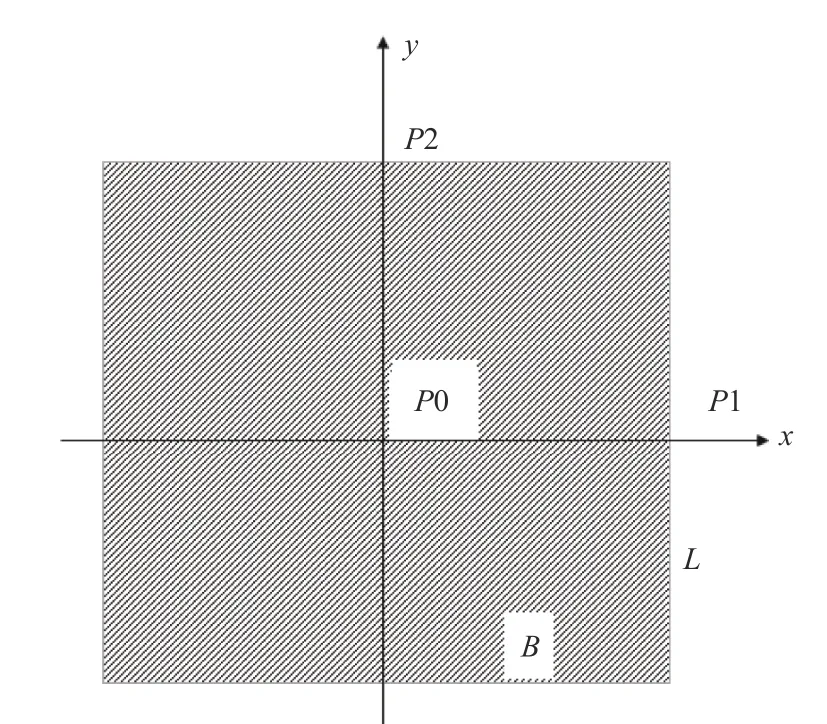
图8 参数依赖点示意图Fig.8 Parameter relative points

图9 载荷5 t时压力分布曲面Fig.9 Pressure distribution under 5 t load case

根据已经得到的参数结果，通过拟合建立参数a和b与载荷的关系式，结合需要满足的条件式（4），可得到参数c与载荷的关系，如式（6）所示。

式中，B，L由式(1)确定。据此即可得到给定载荷作用下轮印载荷的分布特性，结合式（1）确定的轮印几何参数，实现了对设计轮印载荷所需参数的定义过程。

4 数值仿真验证

为验证前文所述针对载重轮胎压力分布规律所提出的轮印载荷分布形式的合理性，采用ABAQUS软件进行仿真分析，对比载荷作用下加筋板的有限元仿真结果与试验响应结果的一致性。

4.1 有限元模型

根据图10建立有限元模型，数值模型包括围板结构和加筋板。材料应力和应变参数来自拉伸试验结果，如图4所示。然后通过静态分析完成计算，计算过程中考虑结构大变形，即仿真模型计算过程中同时涉及材料非线性和结构非线性，通过这种方式来考虑塑性变形对计算结果的影响。模型整体单元类型为S4R，单元尺寸为10 mm×10 mm。为模拟试验模型的边界条件，在螺栓位置处以点约束代替螺栓的固定作用，即

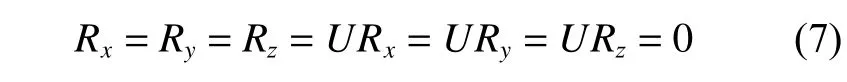
式中：Rx,Ry,Rz分 别为x,y,z方向的平动位移；URx,URy,URz分别为x,y,z方向的转动位移。

根据不同工况的载荷要求，由表2确定相应的轮印尺寸范围，然后依照式（5）和式（6）在轮印范围内施加压力载荷，如图10所示。通过计算即可得出不同工况的仿真结果。

图10 有限元模型及载荷边界情况Fig.10 FEM model and load boundary conditions

4.2 数值仿真与试验结果对比

为了便于对比试验与数值仿真结果的一致性，根据应变测点的位置选定4个截面，分别为横向位置的1，4，7截面和2，5，8截面，纵向位置的1，2，3截面和4，5，6截面，如图11中虚线所示，从而得出每个截面的应力与位置变化关系。在横向上，截面包括3个板格宽度，共600 mm；在纵向上，截面包括1个400 mm纵骨段。

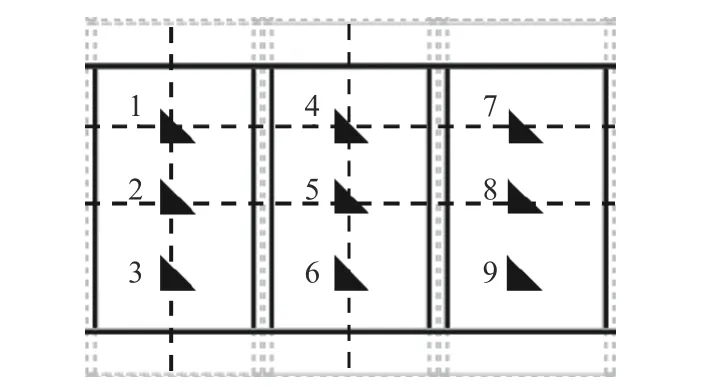
图11 应力截面位置示意图Fig.11 Schematic diagram of the stress section positions

不同载荷对应的应力云图如图12所示，为便于分析，将各载荷对应的应力截面数据整理成如图13至图16所示的结果，图例中T为试验值，S为仿真结果，T2表示W=2 t时的压力试验值，S2表示W=2 t时的压力仿真值。位移结果则以位移−载荷曲线的形式呈现，如图17所示。从图13至图16中可以看出，无论在横向还是纵向，仿真结果和试验结果的应力分布规律和变化趋势具有很好的一致性；位移变化趋势也有很好的一致性，从而证明了轮印分布规律假设的合理性。造成仿真值与试验值差异的原因主要有模型残余应力和残余变形等因素。

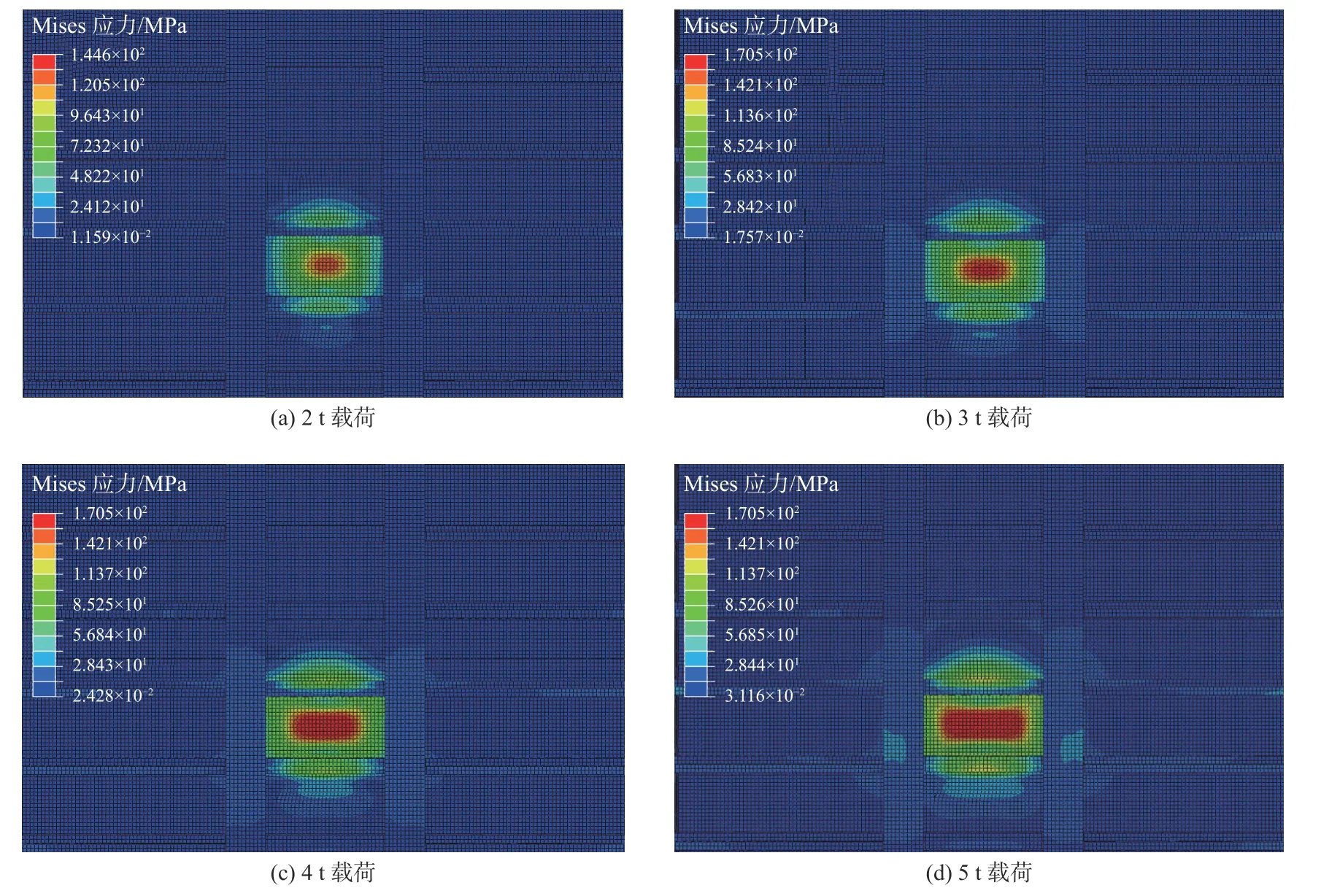
图12 不同载荷下模型应力分布云图Fig.12 Mises stress contours of model under different load cases

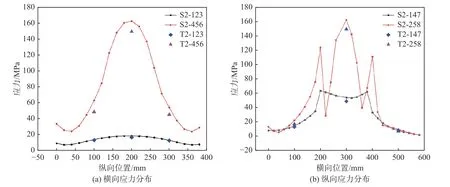
图13 载荷2 t时各截面仿真与试验应力对比Fig.13 Comparison of simulation and test stress of each section with 2 t load

图14 载荷3 t时各截面仿真与试验应力对比Fig.14 Comparison of simulation and test stresses of each section with 3 t load

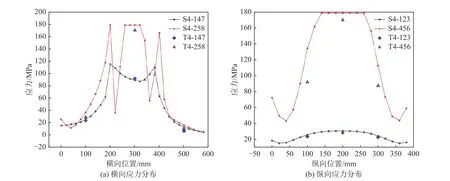
图15 载荷4 t时各截面仿真与试验应力对比Fig.15 Comparison of simulation and test stress of each section with 4 t load

如图13至图16所示，仿真计算的应力关于横向位置出现波动。在258截面应力随横向位置变化的曲线上，共出现3个峰值，其中第1，3个峰值处于加筋板纵骨所在位置。由此可知，在中间板格内，应力主要集中在板格中心区域，在靠近纵骨的区域形成了低应力区。这是因为，纵骨刚度相对较高，加载后变形更小，纵骨附近的载荷将主要由纵骨承受，表现为纵骨附近面板的应力向纵骨集中。中间板格是主要加载区，板格中心区域承受较大载荷，从而在靠近纵骨的区域形成低应力区，造成曲线出现波动。而147截面之所以无此现象，主要是因为该部位并非加载区，且应力水平较低，不存在明显的应力向纵骨集中的问题。而加筋板试验时无法通过应变片监测所有区域的应变，只能选取一定数量的特征点。通过与仿真结果对比特征点处的应力值，即可达到试验和仿真互相验证的目的。

图16 载荷5 t时各截面仿真与试验应力对比Fig.16 Comparison of simulation and test stress of each section with 5 t load

图17 位移−载荷曲线仿真与试验结果对比Fig.17 Comparison of simulation and test displacement with load

5 结 论

本文通过轮印载荷作用下加筋板轮压试验对载重轮胎在加筋板上的轮印载荷分布特性进行了研究，并结合数值仿真进行验证，主要结论如下：

1） 通过试验结果可知，载荷较小时轮印的形状为椭圆形，随着载荷的增大，轮印的形状逐渐过渡到矩形。载重轮胎的轮印压力分布会出现轮印中心区域低于四周区域的情况，呈现出凹型分布的特点。通过总结文献并结合试验结果，提出了加筋板轮印载荷分布形式和参数确定方法，并给出了轮印载荷分布特性的定量表达式。

2）在进行轮压试验时，通过围板与带肋槽钢结合的结构，可以实现加筋板固支边界条件。这种结构相对简便，易于加工和安装。

3） 通过对该分布特性的数值仿真计算，加筋板应力分布特性与试验结果一致性较好，验证了本文给出的轮印载荷分布特性表达式的合理性。所提出的轮印载荷分布特性研究方法具有一定的推广价值，对工程实际应用有一定的参考意义。