大型厂站模块陆地运输易损性分析

李 虎，王传平，刘 涛，兰旭彬 ，库尔班艾力·吐拉甫江，刘鑫瑞

1.新疆油田公司采气一厂，新疆 克拉玛依 834000；2.西南石油大学·石油与天然气工程学院，四川 成都 610500；3.中石化石油工程设计有限公司成都分公司，四川 成都 610031；4.中国石油辽宁销售分公司，辽宁 沈阳 110000

引言

近年来，随着油气资源开发逐渐向偏、远、散地区发展，其开发环境越来越恶劣，多井低产格局日益严重，且地面工程建设面临着有效建设工期短、社会依托薄弱、安全系数低及环保任务艰巨等种种挑战，不再适应这种滚动开发，快速投产，实现效益的要求。

而对于大型天然气处理厂站的模块化建设，将其全部或部分环节划分为多个不同的具有特定功能的模块，在厂内进行预制、组装，并将整体运输至现场，以成品形式实现快速组装[1-3]。解决了众多实际难题，规避了传统建设模式存在的弊端。其图1为模块化建造流程图。

图1 模块化建造流程图Fig.1 Modular construction flow chart

针对于模块的运输，已有学者开展了相关的研究工作。黄育琪等[4]采用软件模拟的方式，对大型破碎站模块在陆地和海洋运输过程中受力特性进行研究，利用承载力及变形指标对模块结构运输性能进行验证。沈登龙等[5]利用ABAQUS 模拟软件，基于不同动载荷情况下，对大型模块在海洋运输中受力情况进行分析。肖立等[6]采用SACS 软件，基于浪载和风载多种组合情况下，对LNG 储罐模块驳船运输稳定性进行分析，发现横浪对其结构带来更为严重的影响。钱孟祥等[7]在惯性力与风载组合工况下，利用SACS 软件，对海洋平台生活模块的海上运输进行模拟，对其结构进行强度校核。综上所述，目前模块运输研究主要集中于海洋运输，对于陆地运输情况较少，且大都对运输过程中结构的形变、受力情况加以说明，还没有涉及结构发生损伤概率分析，即易损性分析。

因此，本文以某一厂站模块陆地运输为例，基于多种实际工况，对运输过程中模块进行瞬态模拟，分析其结构形变情况；并在此基础上，针对不同模块重量，进行易损性分析，获取其发生不同损伤状态的概率曲线。为模块运输设计方案提供理论支撑，为最终的投产运行提供保障。

1 模块运输有限元模型建立

1.1 载荷工况分析

在运输过程中，基于突发的交通状况、多变的天气情况等不可控因素的影响，即使再完善的运输方案，也难免会因突发事件的到来，而对钢结构带来不利的影响。因此，本文对以下载荷情况加以说明，并以此为基础，进行瞬态分析。

1.1.1 针对模块内构件整体重量

由于运输、吊装等多方面因素限制，模块空间是高度集成、有限的，且本次主要是对模块运输过程中整体结构的形变加以分析。因此，本文选取其中质量较大的模块，在建模时，忽略其内部所有构件的外形结构，只考虑整体重量所带来的影响，且为更加贴合实际情况，按不同比例非均匀的按顺序施加于底面横梁A/E 处，整体重量相关数据如表1所示。在简化建模，节省运算时间的同时，使其更具有通用性。

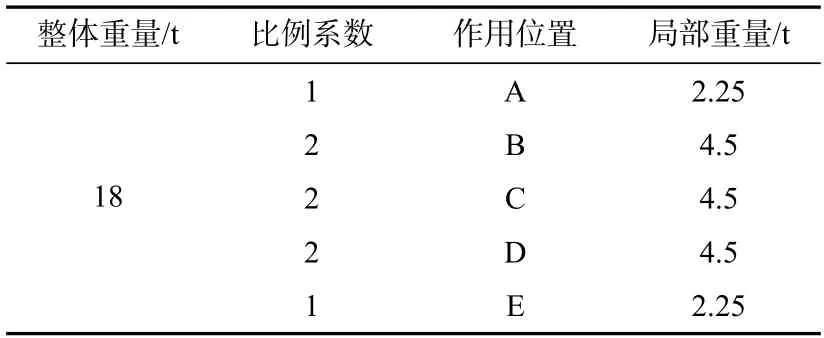
表1 一定比例系数下模块内重量Tab.1 Weight in skid with certain proportion coefficient

1.1.2 针对运输过程中产生的加速度

本次模拟中所涉及工况是基于加速度改变来实现的，所施加的加速度时程如图2 所示。

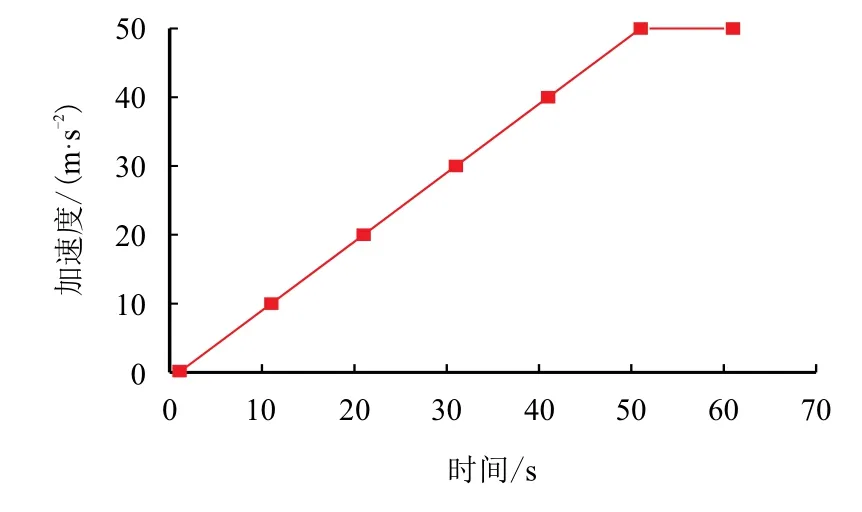
图2 运输中加速度情况Fig.2 Acceleration during transportation

由于模块过大的外形尺寸及重量，运输时，其车辆的缓慢启、制动及途中匀速行驶都是十分有必要的。

但面临突发的交通状况及不良的路况等外界因素的干扰时，不可避免的会因紧急制动而产生惯性力、加速过弯而产生侧向滑移、驶过凹凸路面产生颠簸等，对模块的钢结构带来影响[8]。

1.2 模型建立

为避免运输过程中存在较大位移、形变，本次模拟中钢结构的本构方程采用双线性随动强化模型Bilinear Kinematic Hardening，相关材料参数如表2所示。

表2 钢结构材料相关参数Tab.2 Relevant parameters of steel structure materials

利用beam 单元，根据实际数据定义钢截面尺寸，并在建模过程中，注意梁单元的偏置情况，使其与实际比例相符。

在模块钢结构底部8 个连接处施加全位移约束。对于载荷，除考虑钢结构本身重量之外，还将模块内构件的整体重量，等效为等质量的mass 单元[9]，建立节点间的刚性耦合，通过耦合传递，把质量非均匀的施加于底面，其所建立的模型，如图3所示。

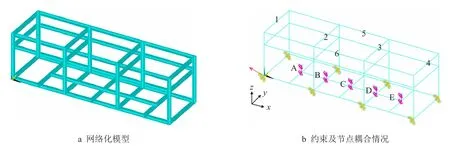
图3 模型示意图Fig.3 Model diagram

并依据图2 中加速度情况，以多步载荷形式施加于整个模型，实现模块运输过程中的瞬态模拟。

2 模块运输稳定性分析

2.1 紧急制动时瞬态分析

由图4 可知，当模块运输过程中发生紧急制动时，其整体存在沿x轴正方向的加速度，具有向右移动的趋势。而相比于底端钢结构存在固定约束，其上部产生较大位移，且随着加速度的增加，首先在梁1、4 中端处出现较大值，然后对其周围横梁产生牵引作用，并有向下延伸的趋势，使其整体位移量逐渐增大。在1 s 时，其加速度为0，模块与运输车辆处于相对静止状态，只有底部构件连接处由于重量产生的惯性作用而产生一定位移量，且在节点23 826 处出现极值（1.47 mm）。因而，在运输途中，应尽量保持匀速运动，且可降低模块与车板间距离，并使其重心相重合，方可减少因加速度变化而产生过大形变。而底部与模块内构件相连处，由于其过大的重量，当加速度a≤24 m/s2，其重力作用起主导地位，且在向下移动的同时，整体向右挤压，25 s时，在右端E 点处产生极值，其值为4.17 mm。随着加速度的进一步扩大，模块左端处于牵引状态，在梁1 中端节点5 108 处出现峰值，51 s 时，其值为8.66 mm。因而，应在此处多加防护。此外，在30 s左右时，A 点处位移矢量处于水平状态，代表着此处构件重力沿z轴方向作用的抵消。

图4 紧急制动情况下不同时刻总位移矢量图Fig.4 Vector diagram of total displacement at different times under emergency braking

如图5a 可知，随着加速度的增加，各点x向位 移均匀增大。

图5 构件连接处各点位移时程曲线Fig.5 Time history curve of displacement at each point of component connection

51 s 时在E 点达到最大位移量其值为7.95 mm，C 点最小，其值为7.62 mm。而在52～61 s 段内，处于匀减速过程，其位移量基本无变化，进而在运输途中应尽量避免急起、停现象的发生。

由图5b 可知，1 s 时，模块整体处于相对静止状态，其z方向位移量由重力作用而产生，因而，A/E两处其值均为1.05 mm；且相比于B/D 处两端受固定约束限制，C 点处位移量更大，达到1.47 mm。

随着加速度的增大，沿x轴出现正压负拉现象，进而A 点处位移反增，且在30 s 左右，其位移量为0，印证了上述说明；而相比于E 点处位移量持续的增加，B、C、D 三点z方向位移量受其加速度影响较小，基本维持不变。

2.2 加速过弯时瞬态分析

针对模块加速过弯，以图2 的加速度时程为根据，对其整体施加沿y 轴正方向的加速度。

由图6 可知，当加速度a≤3 m/s2，其模块重量产生的惯性力起主导作用，位移极值出现在模块底部与构件相连处，4 s 时，节点24 402 位移量达到最大，其值为1.52 mm。

图6 加速过弯时不同时刻总位移云图Fig.6 Cloud chart of total displacement at different times during acceleration of turning

随着加速度的逐渐增加，沿y 轴整体呈现正压负拉现象，位移峰值点上移，出现在梁6 中端节点24 377 处，52 s 时，其值为20.42 mm，亦是整个过程中的最大值，应在此处做好防护工作。

由图7a 可知，随着加速度的递增，各点y 方向位移呈近线性增加。

在51～61 s 段内，加速度保持恒定，其各点位移量基本无变化，且在C 处出现位移峰值点，其值为4.79 mm。

由图7b 可知，当模块处于加速过弯状态时，各点z方向位移量受其影响较小，其值只在小范围内波动，并无明显变化。同时，基于各点所承受重量及其约束作用，A/E 和B/D 曲线重合较好，因而，在设计捆绑方案时，要做到均匀对称，避免因约束不均而导致运输过程中产生不可控位移，对模块带来损伤。

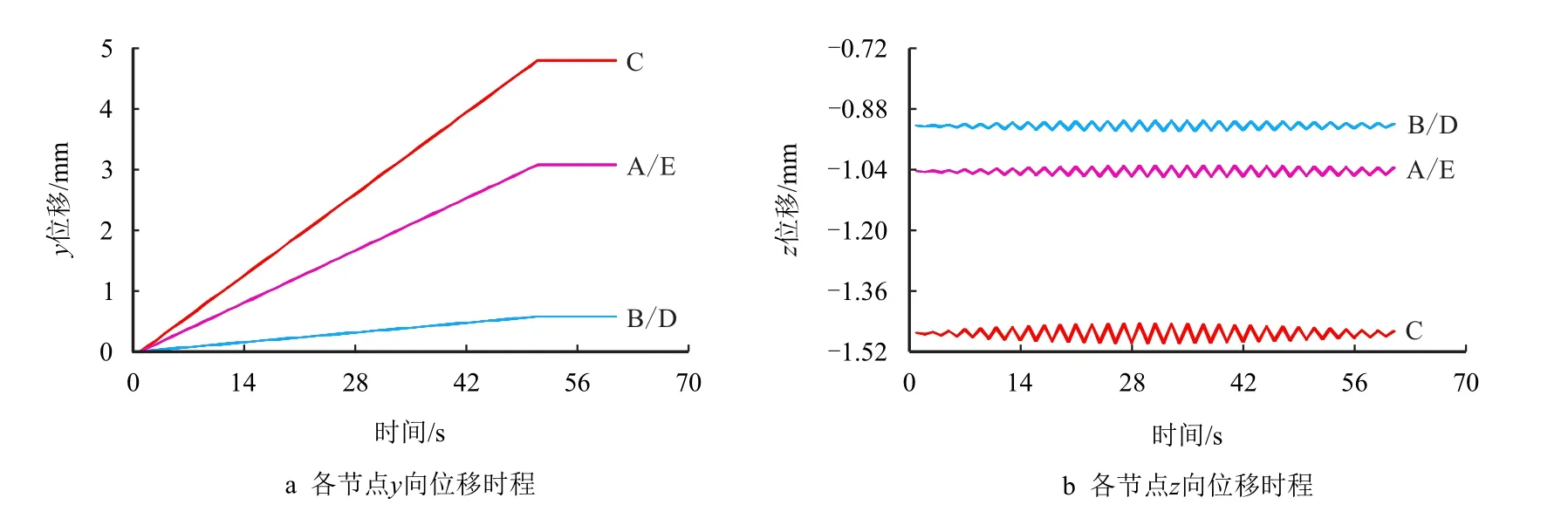
图7 构件连接处各点位移时程曲线Fig.7 Time history curve of displacement at each point of component connection

2.3 驶过凸路面时瞬态分析

模块在运输途中驶过凹、凸路面时，其产生的加速度是沿z方向的，即对重力的叠加，对模块所产生的作用是相似的，因此，为简化篇幅，本小节主要针对驶过凸路面情况进行数值模拟。

由图8a 可知，当模块驶过凸路面时，因加速度变化所产生的位移量主要集中于底部与构件相连处，且在邻近中心节点23 826 处出现极值点，52 s时，总位移达到峰值，其值为9.11 mm。而由于上部梁结构重量相对较轻，所产生的位移量甚微，与其相对静止状况十分相似。由图8b 可知，底部构件相连处各点位移均沿z轴负方向增大，52 s 时，在C 处达到峰值，其值为9.00 mm，且A/E、B/D 处位移曲线完全重合。

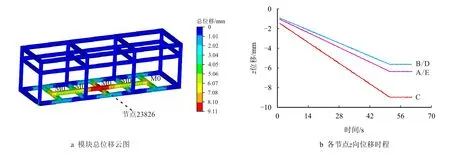
图8 位移云图及构件连接处各点位移时程曲线Fig.8 Displacement nephogram and displacement time history curve of each point at component connection

3 模块运输易损性分析

3.1 易损性分析流程

易损性概念最早出现在军事领域，用来描述飞机、船体对物理碰撞的脆弱程度[10]。经过长期的发展，已有大量学者对结构进行易损性分析，其主要涉及自然灾害对现有结构的损伤程度的研究，如风载[11]、震载[12]等。在本节中，笔者将借此概念对模块运输过程中产生的不可控加速度对其结构带来的损伤加以分析，其整体思路为：（1）基于不同工况，建立仿真模型，获取实时数据；（2）分析加速度与结构损伤函数关系式，并计算出损伤概率；（3）绘制运输过程中模块易损曲线。

针对于结构的损伤程度，主要通过损伤模型加以计算，本节借鉴前人成果[13-14]，采用构件最大位移量加以描述，兼顾结构破坏结果及运输过程中的损伤积累，其构件、模块损伤值计算模型如下所示

式中：xi运输过程中构件最大位移，mm；

xy运输过程中构件屈服位移，mm；

xm实际最大位移，mm；

n模块内构件总个数，个；

D构件损伤值，无因次；

I模块损伤值，无因次；

依据损伤值对模块损伤程度进行划分，其量化标准如表3 所示。

表3 不同破坏等级对应的损伤指数Tab.3 Damage index corresponding to different failure levels

3.2 紧急制动时易损性分析

大型厂站模块化建造所涉及模块众多，其重量也各不相同，因此，本节为便于分析，将重量数据化整，分别取10、15 和20 t，并与运输过程中产生的加速度10、20、30、40 和50 m/s2相组合，进行易损性分析，其工况汇于表4 中。

表4 紧急制动组合工况Tab.4 Combined working condition of emergency braking

通过对上述工况进行模块运输过程中的瞬态分析，获取加速度作用下实际最大位移，并通过式1计算出构件损伤值，进而实现对模块整体损伤指数的评估。将损伤指数及加速度对数化，通过Matlab软件拟合出其相应函数关系如下所示。

模块重10、15 和20 t 时，其函数关系分别为

当结构的整体损伤指数大于某个极限状态时，超越极限状态的概率函数Φ (x) 符合标准正态分布[15]，其概率计算如式（3）～式（5）所示。将其与模块损伤指数函数关系式相结合，并通过表3 获取界限值，方可计算出不同模块重量下发生不同损伤状态的概率

式中：Pf失效概率，无因次；

结构响应均值，即此处的整体损伤指数，无因次；

在联考是大学入学唯一管道的年代，对她和我这种普通高中生而言，不管冷热、无论晴雨，都是适合认真念书的天气，也都该认真念书。我和她都有这种觉悟，而且为了避免升学压力太大而导致精神失常，我们也同时有了要常说冷笑话解压的觉悟。

βd、βc结构抵抗能力、响应的对数标准差，其中钢结构取0.4；

Φ(x)标准正态函数。

其易损曲线如图9 所示。由图9 可知，在不同模块重量状态下，其运输过程中易损曲线走势基本相同，都随着加速度的增大，其结构更易发生损坏。当重量为10 t，加速度为10 m/s2时，结构发生轻微损坏的概率为0.62，这是因为对于大型厂站模块化，其重量轻则几吨，重则几十吨，即使存在微弱的加速度，都会破坏运输过程中的平衡状态，给模块带来不可逆转的影响；而发生倒塌的概率为0.12，可见，在加速度较低时，其结构具有一定的抗变能力。当重量为20 t，加速度为50 m/s2时，结构发生倒塌的概率为0.52，较之模块重10 t，增加了13.5%。

图9 模块重10、15 和20 t 下制动时不同加速度下易损曲线Fig.9 Vulnerable curve of skid under different acceleration when braking under 10,15 and 20 t

因此，在进行模块运输方案设计时，应对重量大的模块做好防护工作。

3.3 加速过弯时易损性分析

针对于模块加速过弯易损性分析，选取重量为10、15 和20 t。

与运输的过程中所产生的加速度5、10、15、20和25 m/s2相结合，其加速过弯的组合工况，如表5所示。

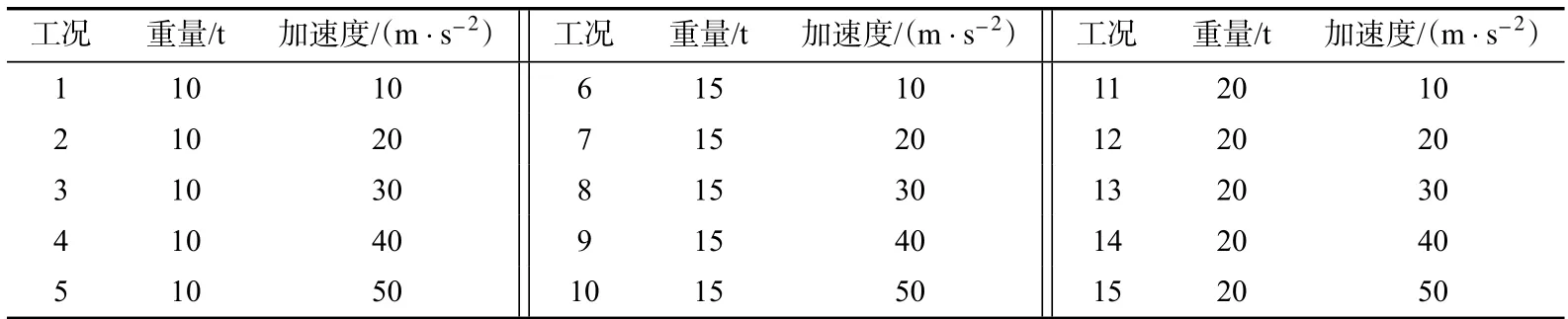
表5 加速过弯组合工况Tab.5 Combined condition of acceleration and bending

基于上述方法，获得的模块重量分别在10、15和20 t。

运输过程中模块损伤指数与加速度函数关系式分别为

结合式3 及获取的界限值，计算出加速过弯时不同重量下模块发生不同损伤状态的概率，其易损曲线如图10 所示。

图10 模块重10、15 和20 t 下过弯时不同加速度下易损曲线Fig.10 Vulnerable curve of skid under different acceleration when it is bent under 10,15 and 20 t

由图10 可知，在不同重量下，相比于制动情况，其不同损伤状态易损曲线趋势基本相同，即随着加速度的增大，结构发生损坏概率也有所增加。当模块重10 t，加速度为5 m/s2时，发生轻微损坏的概率为0.78，而发生倒塌概率较小。

模块重20 t，加速度为25 m/s2时，发生倒塌概率为0.44，较之重量为10 t，增加了11.5%，较之制动情况（重量为20 t），增加了29.1%。可见，在相同条件下，过弯过程中产生较大加速度对钢结构所带来的影响更为严重。

4 结论

（1）在进行紧急制动、加速过弯瞬态分析时发现，当加速度分别为a≤24 m/s2和a≤3 m/s2，其模块重量产生的惯性力起主导作用，且随着加速度的增加，上部梁中端处先发生移动，并牵引着周围梁，使其整体位移量加大。因此，针对受力情况，应对上部梁加强防护，防止产生较大形变。

（2）紧急制动时，其加速度对底部构件连接处中端（B、C、D）沿z方向的位移量影响甚微，而模块整体呈现沿x轴正压负拉现象，使其A 处位移量反增，E 处持续增大，是与实际情况相符的。但在加速过弯时，加速度对底部各连接处沿z方向的位移量影响较小，与静止状态相似。

（3）在进行模块易损性分析时发现，不同重量下，发生不同损坏状态时的易损曲线趋势基本相似，即随着加速度和重量的增大，钢结构发生损坏的概率也在增加。同时，通过对比发现，在相同条件下，加速度对模块过弯时产生的损伤影响更大。