先用整体法还是先用隔离法
——连接体问题中研究对象的选择顺序
张克文
(滦南县第一中学,河北 唐山 063500)
1 提出问题
物理学的发展中,贯穿着归一性和简洁性,一类问题的解决方法,若能进行归一,必然能够提高学习效率,减轻学生负担,同时这也遵循着物理学科素养中的科学思维的精神.
连接体问题,指的是存在相互作用的几个物体组成的系统,是高中物理的运动和力部分的重点,也是难点.无论是共点力平衡问题,还是牛顿运动定律问题中,出现的频次都是很高的.由于它对学生科学思维为主的各项素养的培养和考查中,具有较好的有效性和较高的区分度,所以,考查频度很高.可是学生面对连接体问题时,总是感觉无从下手,困难重重.那么学生解决连接体问题遇到的主要障碍是什么呢?
在教学过程中我们发现:对于这些运动和力问题的解决,学生都掌握了分析和解决问题的步骤和基本方法,如果是单个物体的问题,由于不涉及研究对象的选择,学生解决问题是比较顺利的.而面对连接体问题时,学生的困难主要在于不知道先研究哪个对象才能使问题的解决更顺利,即不清楚研究对象的选择顺序.
2 问题的分析
学生在学习中往往有这样的经验:连接体问题应该运用整体法和隔离法来解决,有时先整体后隔离,有时先隔离后整体,需要具体问题具体分析.核心问题是先选择哪个物体作为研究对象,才能使问题得到解决,或解决得更顺利,即研究对象的选择顺序是成功高效解决连接体问题的关键.这里本文通过几个简单实例的分析,来探讨一下:连接体问题中,研究对象的选择顺序有规律性吗?按照怎样的顺序选择研究对象,会使连接体问题的解决更高效呢?
2.1 问题的初探
例1.如图1所示,水平路面上有一辆载货汽车,质量为M=1.6×103k g,车上又装载一物块,质量为m=0.4×103k g.已知汽车原来处于静止状态,开始加速的瞬间,牵引力的大小为F=1.0×104N,并且物块在车厢内恰好没有发生相对滑动,不计地面及空气对系统的阻力.求物块与车厢之间的最大静摩擦力?

图1
学生一般会先运用整体法,再隔离物块,可以使问题得到解决.
解析:先研究整体,F=(M+m)a.之后研究物块,fm=ma.所以fm=2×103N.这里我们需要进一步思考,为什么要先整体后隔离?
如果分析两个研究对象的受力及加速度这些物理量的已知和未知情况,就会发现:对于整体,重力、支持力、牵引力为已知,加速度未知;对于物块,重力、支持力已知,摩擦力、加速度未知.即对整体是三个量已知,一个量未知,对物块是两个已知,两个未知,整体的未知量较少,所以研究对象的选择上遵循了由简入繁的顺序.
那么,在其他连接体问题中是否也是由简入繁呢?
2.2 经验的验证
例2.如图2(a)所示,在一些趣味体育活动中有托球跑这个项目.某次活动中,比赛队员手握一支倾斜的板球拍(拍面光滑)托着一只塑料球向前水平运动,球在拍上不动.已知拍的质量M=0.5k g,球的质量m=0.1k g,拍与竖直方向的夹角为θ=37°,g=10m/s2,不计空气阻力及球与拍间的摩擦,求该队员的手对球拍的水平作用力.
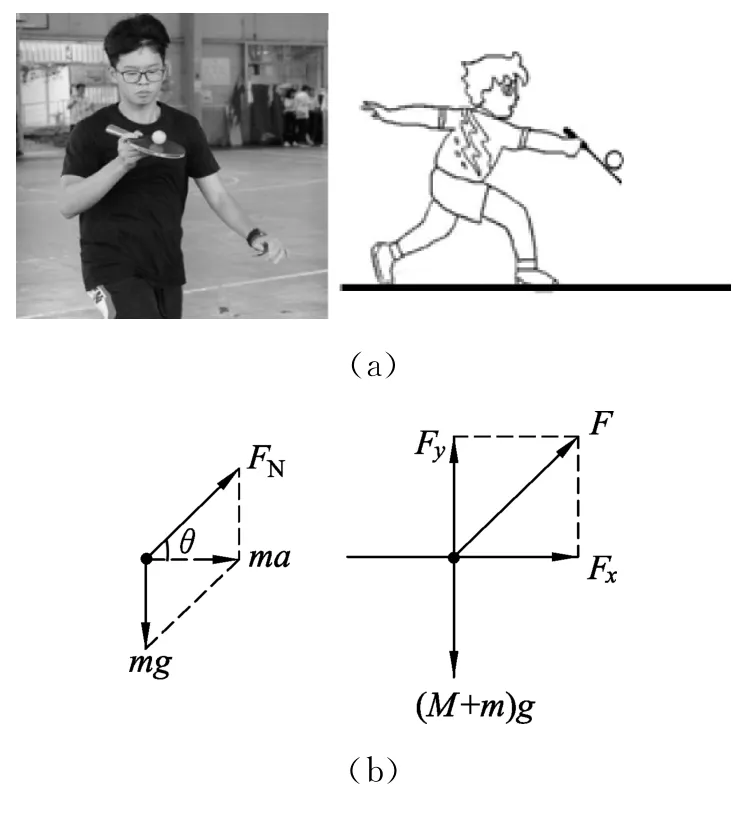
图2
解析:这个题目的解答中,学生一般先隔离后整体,也会比较顺利.先研究球,如图2(b)所示,mg/tanθ=ma.
之后研究拍和球的整体,Fx=(M+m)a.所以Fx=8N.
再来分析两个研究对象的受力及加速度的已知情况,对塑料球,重力和各力之间的夹角为已知,加速度未知;对整体,仅重力已知,Fx、加速度、角度均为未知.即先研究了已知多、未知少的塑料球,后研究未知多、已知少的整体,研究对象的选择上仍是遵循了由简入繁的顺序.
上面是两个各物体具有相同加速度的连接体问题,对于加速度不同的问题,加速度已经不能作为物体间联系的纽带,研究对象的选择是否还遵循由简入繁的顺序呢?
2.3 举一反三
例3.山区雨季常发生泥石流,处在山坡上的人会本能的采取一些措施来避险.下面为一简化后的模型:如图3所示,固定光滑斜面倾角为θ,上面放一长木板,木板上的人沿板向上奔跑,可使他自己相对地面静止.已知人的质量m,木板的质量M,重力加速度g,求木板的加速度?
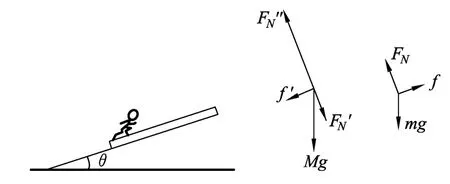
图3
学生的正确解答:先选择人作为研究对象,后选择木板作为研究对象.先研究人,f=mgsinθ.之后研究木板,f′+Mgsinθ=ma.f′=f.所以a=(M+m)gsinθ/M.
两个研究对象的受力及加速度的已知情况,对于人,加速度为0、重力、斜面的倾角已知,静摩擦力未知,未知量较少;对于木板,重力、倾角θ已知,摩擦力、加速度未知,未知量较多.所以要先选择人作为研究对象,后选择木板作为研究对象.同样也遵循了由简入繁的顺序,只是前后联系的纽带是相互作用的摩擦力.
2.4 经验的升华
再从另一个角度分析,既然研究对象的选择顺序是由简入繁,那么,这样选择还会有其他效果吗?
例1中,通过对整体的分析,可以求得加速度,而它也是物块的加速度.本来物块的相关条件中,有加速度a、摩擦力fm两个未知量,由整体求得了加速度,使得物块的未知量减少了一个,也就是物块的已知量增多,只剩下摩擦力一个未知量,使复杂问题降低了难度,成为简单问题.
例2中,由简入繁也起到了这样的作用:通过对塑料球的分析,得到了加速度这个物理量.在研究整体和球的整体时,增加了加速度这个已知量,使得球拍的未知量只剩下水平作用力,起到了降低难度的效果.
例3中,通过对人的研究求得摩擦力后,由于摩擦力是人和木板间的相互作用力,通过运用牛顿第三定律,使木板的已知条件增加,只剩下加速度这个未知量,从而变成了简单问题.
也就是说,由简入繁,这个选择研究对象的选择顺序,同时起到了这样作用:简单问题的分析中,求得一个新的物理量,为复杂问题的分析,增加了一个已知条件,使得复杂问题变得简单.因此由简入繁更大的意义是由简助繁.
3 方法总结归一
总结:通过分析以上3个实际问题不难发现,
(1)研究对象的选择顺序:由简入繁.简,指力及加速度等物理量中,已知量的个数多、未知量的个数少的那一个研究对象.
(2)“简”会为“繁”增加已知条件,使繁变简.即由简助繁.
(3)助的途径是通过相互作用力或加速度之间的联系来实现.
4 实战演练
懂得了由简助繁的道理,解决连接体问题时,就能迅速而恰当地选择研究对象,解决问题的效率就会大大提高.例如:
练习题1.2022年我国将承办冬奥会,滑雪项目中,运动员乘滑板沿倾斜坡面自由下滑,如图4,已知运动员和滑板的质量分别为M和m,坡面倾角为θ,不计空气阻力及坡和滑板间的摩擦力,求运动员和滑板间的摩擦力是多大.
图4
将总结的经验用于实战演练,在运用中提高能力.
对运动员、滑板或整体的受力分析发现:由于物体间的摩擦力及整体的加速度未知,若采用隔离法,若选择运动员或滑板作为研究对象,均有加速度、摩擦力两个未知量;而选择整体为研究对象,则只有加速度为未知量.所以选择研究对象的顺序应为:先选择整体,后隔离运动员,问题可顺利解决.
练习题2.用两根轻质绝缘细线将两个质量相同的小球P、Q悬挂起来,放在水平向右的匀强电场中,使P、Q分别带上等量的正负电荷后,系统处于静止状态.则两球的状态可能是图5中的哪一个?

图5
4个选项中,确定两条细线的方向,即拉力的方向,就可以选出正确的答案.所以选择整体,可以避开P Q间的细线拉力这个未知量,很容易地确定出上段细线拉力的方向,而研究Q则可以迅速得出P Q间拉力的方向.
练习题3.如图6所示,水平力F拉A、B、C3个物体在光滑水平面上运动,在中间的B物体上加一块橡皮泥后,它和B的物体一起运动,且原拉力F不变,那么加上物体以后,两段绳的拉力Ta和Tb的变化情况是
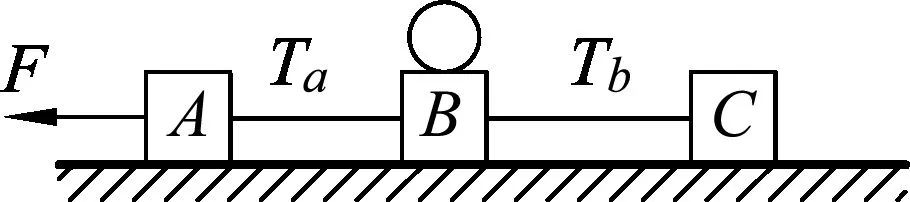
图6
(A)Ta增大. (B)Tb增大.
(C)Ta减小. (D)Tb减小.
这个问题中,Ta、Tb均为未知,因此先选择整体为研究对象,可求得加速度a的变化.为隔离各物体增加了一个新的物理量.Tb的分析,可选择C作为研究对象;Ta的分析中,若选择B及橡皮泥为研究对象,存在两个变量m、a;可以选择A为研究对象,此时未知变量只有Ta,可顺利求出结果.
不只在连接体问题的分析中有由简助繁的思想,其他问题中,也广泛贯穿由简助繁的思想,例如:
练习题4.如图7所示,轻杆长L,一端装光滑轴O,中点及另一端固定A、B球,从水平位置由静止释放,摆至竖直位置时,A、B速度各多大?杆对B做多少功?
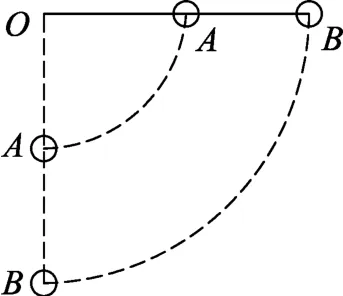
图7
这是一个功和能的问题,由于AB间杆的作用力、两球的末态速度均为未知,所以,应先研究整个系统,运用机械能守恒定律得出两球的速度,再研究其中一个球,可以顺利地解决问题.
总之,连接体问题中,在研究对象的选择顺序上,应遵循“由简入繁”的顺序,同时可以起到“由简助繁”的效果,使得连接体问题的解决不再盲目,不走弯路,变得简捷而高效.

