创设真实情境 培养科学思维
蔡 钳 陈继红 曹卫东 周 攀 陈信余
(1.华南师范大学附属中学,广东 广州 510000;2.广州教育研究院,广东 广州 510062;3.广州大学附属中学,广东 广州 510006;4.广州执信中学,广东 广州 510062)
情境,是教学的重要载体.物理学科的教学离不开情境.情境,也是普通高中物理课程改革中出现频率极高的一个词,不管是教学,还是考试,情境化是一个重要的方向.《普通高中物理课程标准(2017年)》(2020年修订)在各章节的教学建议中均提出要创设情境进行教学,这体现了基于情境展开教学活动的重要性.
要培养科学思维,需要创设什么样的真实情境?要如何基于真实情境展开师生活动?科学思维包括模型建构、科学推理、科学论证和质疑创新等要素.那么,情境的创设应根据课程目标的需求,有意识地指向这些要素的培养.
下面,通过理论归纳与实例展示落实科学思维素养目标的做法.
1 重视模型建构过程的师生活动
模型建构能力是应用物理学知识解决问题的重要能力,要解决实际问题,首先必须能够从物理学的视角认识问题,进而将实际问题转化为物理模型,然后调用物理规律解决问题.模型建构能力的培养,最重要的是要突破从现象到物理模型的思维距离(图1).

图1
《思维的模式》一书将人类接触现象的过程描述为:“重要性(指人类对事物最突出的印象)”—“表达”—“理解”3个步骤.具体到物理模型的建构,可以将这一思维过程拓展为“印象”—“描述”—“理解”—“抽象概括”—“形成模型”5个步骤.也就是说,从现象到物理模型,应该给予学生最突出的感官印象、充分的描述和表达的机会、理解的时间和空间、抽象概括的过程以及构建物理模型的结果.这样将能够顺利突破上文所说的思维的距离.
下面,以“圆周运动”的一个教学实例展示这个思维过程.
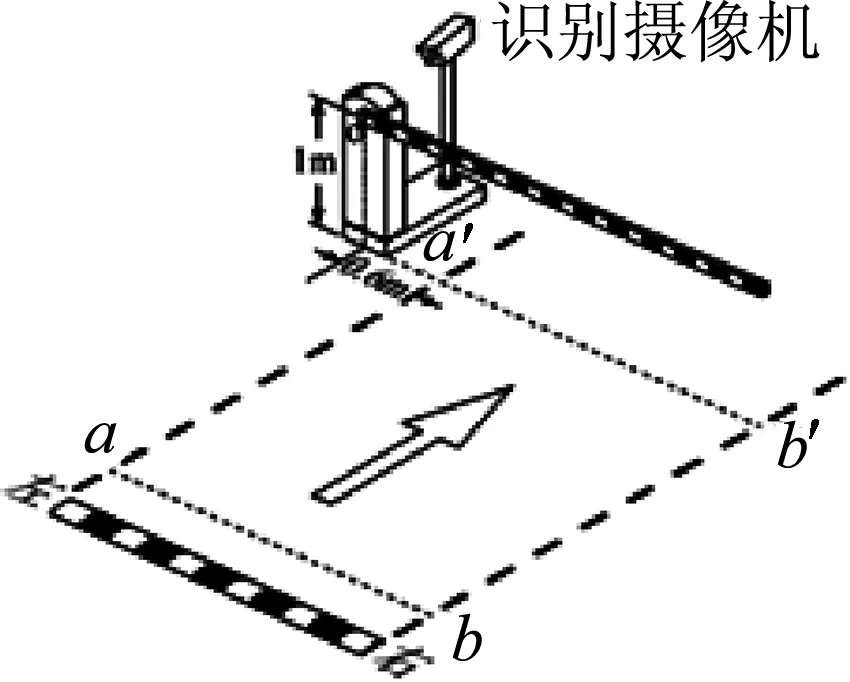
图2
案例1.如图2,带车牌自动识别系统的直杆道闸,离地面高为1m的细直杆可绕O在竖直面内匀速转动.汽车从自动识别线AB处到达直杆处的时间为3.3s,自动识别系统的反应时间为0.3s;汽车可看成高1.6 m的长方体,其左侧面底边在a a′直线上,且O到汽车左侧面的距离为0.6m,要使汽车安全通过道闸,直杆转动的角速度至少多大?
下面通过表1展示教学活动的过程.
上述教学活动中,基于学生对物理模型建构的各个不同的思维阶段,给予学生相应的启发.整个教学过程围绕这样一个思路:汽车不碰到杆的直观感受——汽车不碰到杆的物理条件——用物理模型建构一个汽车不碰到杆的图形——应用已有的物理模型解决问题.在每一个阶段,教师应给予学生充分的思维空间和时间,力求最大程度的让学生经历物理模型的建构过程.
值得注意的是,上述的教学过程虽然侧重了模型建构能力的培养,但也涉及了分析(对汽车高度、距离以及角度大小的分析)、推理(推出杆转动的时间、杆恰好越过汽车等结论)等思维过程.一个教学事件的发生,必然涉及学生各方面的素养,只是教师根据不同的素养目标的预设,开展侧重点不同的教学活动,从而较好地落实目标.
2 重视科学推理的思维过程
科学推理是科学思维的重要体现,是科学思维的“显性动作”.推理,包括是从一般到特殊的演绎推理、从特殊到一般的归纳推理、从类似的现象进行迁移的类比推理.下面通过教学实例探讨基于真实情境进行推理的教学活动.
在探究重力做功是否跟路径有关的问题中,在教师的引导下,某实验小组对重力做功与路径无关产生质疑,想从真实实验情境中证实这个结果,于是设计了下面几组真实实验情境进行探究.
该小组通过表2中的3个不同情境的实验,发现v1与v2几乎相等,v3略小一点,但误差范围内v1、v2、v3可以视为相等.
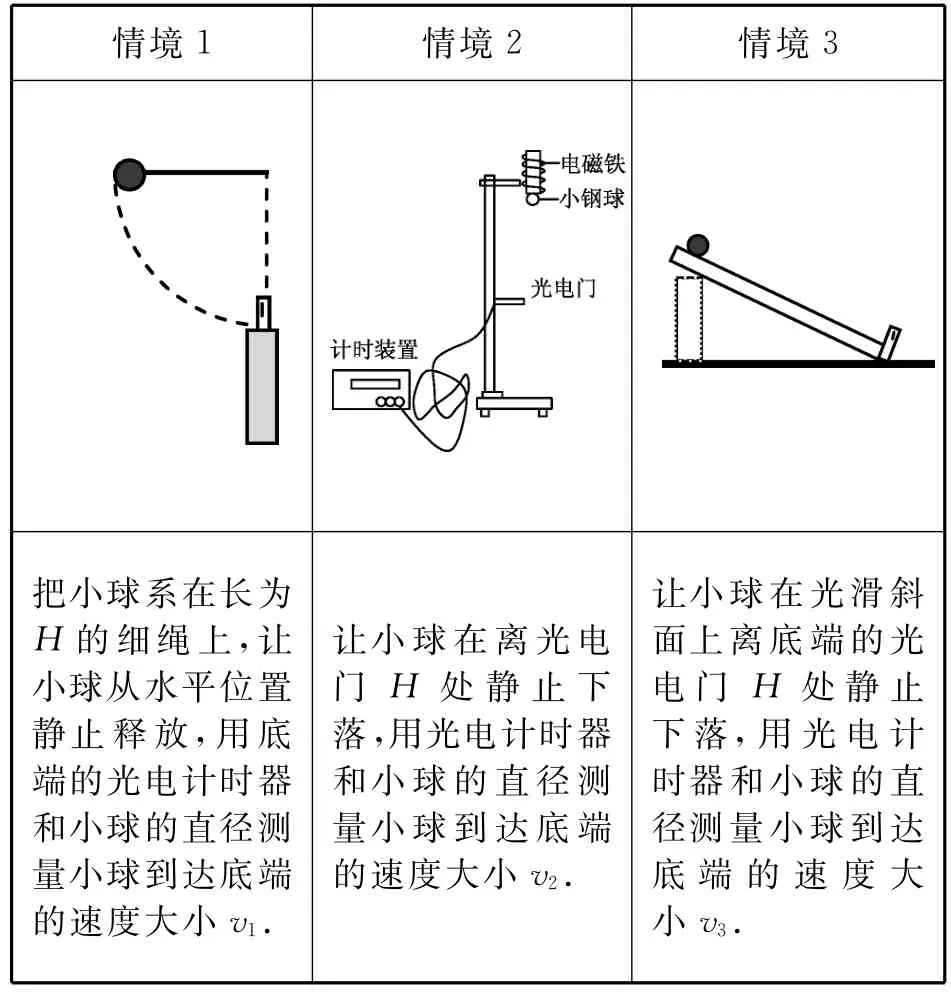
表2
教师引导学生进行推理:情境1中小球沿着圆弧路径运动、情境2中小球沿着竖直路径运动、情境3中小球沿着光滑斜面运动,从小球到达斜面底端的速度相等这个事实,同学的结论是什么?
学生:小球沿着3个不同的路径到达光电门处,但路径的高度差一样,小球到达底端的速率也一样.这说明这3种情况重力对小球做功的大小相等.
教师:那么,我们是否可以将这个结论进行这样的拓展:如果小球沿着其他路径运动,只要高度差一样,重力做的功相等.从理论上是否能够论证这一结论?
师生交流:如图3,小球沿着不规则的曲线轨道下滑,下滑的竖直高度为H,重力对小球做功多大?

图3
根据功的定义:力与沿着力方向的位移的乘积,可以轻松得到重力做功为m gH,这与前面的3个实验的结果一致.
可以进一步探讨:如图4,将曲线轨道分为无数段无限小的轨道,每段轨道可以近似为直线轨道.第一段轨道长ΔL1,其与竖直方向夹角为θ1,根据功的定义,重力做功为mgΔL1cosθ1=mgΔH1,从而可得小球从轨道顶端下滑竖直高度为H的过程中,重力对小球做的功为W=mg(ΔH1+ΔH2+ΔH3+ΔH4+…)=mgH.
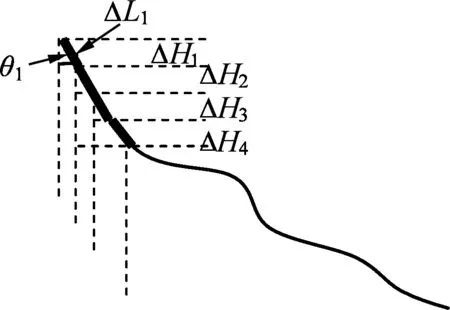
图4
上述教学过程,通过3个真实的情境获得3个特定的结果,在通过结果的比较演绎推理得到重力做功与路径没有关系的初步结论.这是在足够多的“感性材料”的基础上,运用推理的思维方式获得的初步结论.接着,质疑结论的普遍性:通过这3个情境得出的结论是否能够得出一个普遍成立的规律?于是,教师运用功的定义和公式结合数学方法进行多角度的分析,最终得到一个令学生信服的结论:重力做功与路径无关,等于重力与高度差的乘积.
教师进而向学生提出一个更普遍的问题:是否与重力性质类似的力做功,其大小都与路径无关?
这一过程,让学生经历了一个结论形成的完整的思维过程:从感性材料出发,一步步演绎、推理,结合定量分析,最终归纳得出结论,这对培养科学推理能力、落实科学思维素养目标的培养是有效的.
同样的,上述教学不仅仅局限在科学推理这一要素,其中也涉及了质疑、论证等方面思维的启发和培养.也就是说,任何教学过程对学生思维发展的影响都不是孤立的,而是全面的,只是教师在教学过程中侧重点不同而促使教学目标指向不同.
3 重视质疑创新的问题情境
质疑是科学发展的重要动力,提出问题比解决问题更重要已经成了一种共识.在质疑的基础上,思考、寻找解决疑问的方法,最终得到解决问题的策略,就是一种创新.下面,通过一个基于真实情境的习题的教学案例,探讨培养学生质疑创新能力的一种方式.
案例2.如图5,单人双桨赛艇比赛中,运动员用双桨同步划水使赛艇沿直线运动.运动员每次动作分为划水和空中运桨两个阶段.假设划水和空中运桨用时均为0.8s,赛艇(含运动员、双桨)质量为70k g,受到的阻力恒定,划水时双桨产生动力大小为赛艇所受阻力的2倍.某时刻双桨刚入水时赛艇的速度大小为4m/s,紧接着运动员完成1次动作,此过程赛艇前进8m.求

图5
(1)划水和空中运桨两阶段赛艇的加速度大小之比;
(2)赛艇的最大速度大小和受到的恒定阻力大小.
该题的解答过程比较简单,题目已经将赛艇的运动抽象成这样的物理模型:划桨时,赛艇做匀加速直线运动;空中运桨时,赛艇做匀减速直线运动.这利用动力学规律不难解答.解完这个问题,笔者觉得这么好的素材情境应该发挥更大的作用,于是向学生提出这样一个问题:大家有没有见过赛艇,赛艇的运动真的是这样的吗?我们把运动过程抽象成先匀加速、后匀减速直线运动的过程,这会不会与现实偏离太大?
问题一抛出,顿时鸦雀无声.显然,学生已经习惯于这样的理想化方式,对于是否合理已经没有思考的习惯了.当然,有个别学生说他也有这样的疑问.
于是,笔者让学生课后去查阅资料,下一节课再来解决问题.
最后,通过查阅资料,有学生找到对赛艇划水比较合理的建模方式:赛艇的运动可以抽象成一个匀速直线运动叠加一个简谐运动,它运动的速度-时间图像大致如图6所示.

图6
于是教师进一步提问:赛艇的真实的速度图像与该题中运动的v-t图差异大吗?
学生在图6中作出了题目所建立模型的运动图像的v-t图,如图7所示,发现两个图像比较接近.教师借机提出这样的观点:简谐运动的图像中,绝大部分与直线非常接近,基于高中阶段的知识限制,把赛艇的简谐运动简化为先匀加速后匀减速直线运动的模型,是可以接受的.这样的结论,得到多数学生的支持,还有少部分质疑的学生,他们会继续钻研、继续查阅资料、继续发现问题,这不就是教学的目的吗?

图7
这一教学过程,不仅能够让学生重新发现一个物理模型简化思路,更能够培养学生对习以为常的事实产生质疑的习惯,引导学生质疑之后寻找解决问题的创新的思路和方法.
4 结论
综上所述,在创设真实情境的教学中培养科学思维,从创设情境到基于情境进行教学,每一个环节都不是孤立的,每一个环节都应该落在学生思维的关键点上,在最恰当的时候进行启发,推动学生的思维顺着预设的教学路径前进.同样,对于培养科学思维的各个要素的教学策略也不是孤立的,模型建构过程需要分析推理,分析推理过程涉及抽象概括,只是选择的侧重点不同罢了.希望上述的案例,能够为真实情境的教学如何培养科学思维提供思路与启发.

