基于场景支持理论的高中物理模型建构
徐卫华
(南通市教育科学研究院,江苏 南通 226001)
前段时间,笔者去某校高三教学调研,听了一节关于“圆周运动”的复习课.这节课中涉及到“圆锥摆”模型的复习,听课后对物理模型建构能力的培养有了些许思考.物理模型是人们在研究物理问题时,为了方便又能突出本质而对研究对象的一种简化和抽象,通常能够再现一类物理现象的本质和内在特性.学生在高中物理学习过程中,对物理概念、规律的建立过程都与相关物理模型相联系.高三物理教学以“问题——情境——模型”为链条的设计是促进学生知识内化、提升学生核心素养的有效策略.如何构建贴合学生学习的问题链,实现物理模型建构能力培养?笔者翻阅文献发现,场景支持理论对高中物理模型深度教学大有裨益.20世纪40年代末,美国堪萨斯大学的心理学家巴克(Roger Barker)和赖特(Herbert-Wright)带领团队建立实验基地,通过研究真实行为场景(behavior setting)对个体行为可能产生的影响,建立场景支持理论.其很多研究成果及相关理论有利于高中物理模型深度学习.
场景支持理论下的高中物理模型学习势必是有意义的、深度的学习.学生在具有开放性的场景中学习,学习过程凸显思辨性和主动性,多触角联系物理模型,深化对物理模型的理解,提高对物理模型认识的完整度,将多个真实的情境进行场景重组,引导学生应用原有模型并进行迁移,在真实性和实践性的场景中实现知识内化,促成核心素养的提升.
1 开放性场景支持,建立相对“完整”模型
无论是新授课,或者是复习课,要想帮助学生建立(或复认)完整的概念、模型均离不开情境或场景支持,而且越是开放的场景支持越能发散学生思维.高中物理新教材,每节内容均以一个生活化的场景抛出问题为探究的发端,其目的就在于给学生提供相对开放的场景支持,引导学生在头脑中主动建立知识与生活的联系.
复习课同样需要场景支持.学生在高一、高二的学习过程中已经涉及到了相关知识,只是在复习前头脑中留下的痕迹较浅、较零碎,对物理模型的认知浮于表层,联想度不够丰富,逻辑推理也不够严谨,容易受表面现象的干扰,或由于思维的表层化导致对模型的认识不完整,甚至忽视了其本质.为了促进学生的有效复认,教师应该给学生提供场景支持,而且在知识复认的初期,场景支持指向具有开放性的问题,借此引导学生尽可能多的复认完整模型.
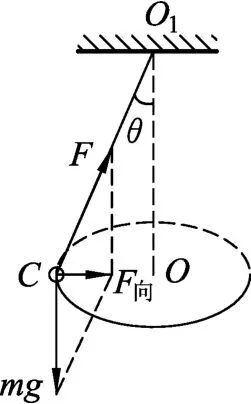
图1
以“圆锥摆”模型为例,提供如图1所示的场景并开放性设问:长为l细线一端悬于天花板O1点,另一端系一质量为m的小球C(可视为质点),小球在细线拉力作用下做圆锥摆运动,当角速度为ω时细线与竖直方向的夹角(摆角)为θ,你能提出哪些问题?
开放性的问题设计能够引导学生从浅层认知逐步向模型的内涵、外延延展,大多学生开始能提出以下几个问题.
问题1:小球作圆周运动的运动参量分别等于多少?
设问目的是复习圆锥摆的圆平面、半径、向心力、向心加速度、角速度等浅层概念.小球在水平面上作匀速圆周运动,圆心在悬点O1的正下方,圆锥摆的向心力由细线拉力F与重力mg的合力提供,能够初步建立r=lsinθ,mgtanθ=man,mgtanθ=mω2lsinθ等关系.
问题2:细线拉力等于多少?
设问目的是厘清圆锥摆运动中参量间的决定关系.由图1中的矢量三角形可知,线中拉力F=通过对关系式的研究,可以发现小球做不同情形的圆锥摆运动,细线等长、角速度相同时,线中拉力大小相同.
问题3:若保持线长l不变,增大角速度ω,线与竖直方向的夹角(摆角)θ将如何变化?
设问目的是复认圆锥摆“摆角”与哪些因素有关.由mgtanθ=mω2lsinθ,可得在受力分析的基础上再往前进一步,帮助学生建立了圆锥摆的摆角公式,线长一定时,转动角速度越大,摆角θ越大.
问题4:求上述圆锥摆运动的周期.
设问目的是推导出圆锥摆运动周期的通式.联系匀速圆周运动基本运动参量的关系,圆锥摆运动周期,再结合,可得出T=
学生通过对上述问题链的分析,不仅能有效复习圆锥摆的向心加速度、角速度等,还能在此基础上,通过引导与比较帮助学生复认较为完整的“圆锥摆”模型.如在问题4中得到周期T=后,将圆锥摆模型与单摆模型相联系,可以建立“等效摆长”的概念:l′=lcosθ,l′为悬点到轨迹圆平面的高度.这个等效摆长又是与生活实践相联系,可以用来分析更为复杂的场景问题(下文中有例题分析).
2 注重场景重组,提升核心素养
加涅认为:“教育课程的最终目标就是教学生解决问题”.给学生提供多组真实的、有联系的场景,学生在研究学习并进行分类时,将问题解决作为学习的高级形式,在相似的场景下能够举一反三,在不同的场景下能够灵活运用,这些均能促进解决问题能力、物理学科核心素养的提升.
重组场景1:共轴双圆锥摆模型.
奥苏贝尔曾说:“当学生把教学内容与自己的认知结构联系起来时,意义学习也便发生了”.开放性场景支持下,学生已经对“圆锥摆模型”有了较为完整的认识,那能不能运用其来解决具体的问题呢?这时需要教师给学生提供更为复杂一些的场景,设置的问题指向性相对明确些,引导学生在场景支持下建模、解决实际问题,提升核心素养.
分析江苏省近几年的高考试题,建模能力的考查要求一直比较高,需要学生对模型有较为深刻的认知.因此,我们的平时教学应注重学生建模意识和能力的培养,通过场景的重组将知识教学与生活中的原始物理问题相联系,引导学生在解决具体问题的过程中实现素养的提升.如2013年江苏高考物理第2题,以生活中“旋转秋千”(如图2所示)为背景,2020年南通物理三模的第5题,以“拨浪鼓”(如图3所示)为背景,本质上均考查学生对圆锥摆模型认知程度.以图2的旋转秋千为例,如果从题目情境中所给的显性化条件“周期相同”,得出“角速度相同”的初步结论,然后再抓住图2中物块B的圆周运动半径大这个要素,从线速度与角速度关系,列出向心力方程是能够得到正确选项的,但学生对模型的理解是不深刻的.图3的拨浪鼓情境分析也是这样.无论是旋转秋千,还是拨浪鼓场景,如果从圆锥摆的周期公式出发,较容易得到等效摆长l′=lcosθ相等,结合情境中悬点的位置差异,让学生类比图1建立等效的圆锥摆模型进行半定量分析,问题的解决变得更为清晰.

图2 旋转秋千
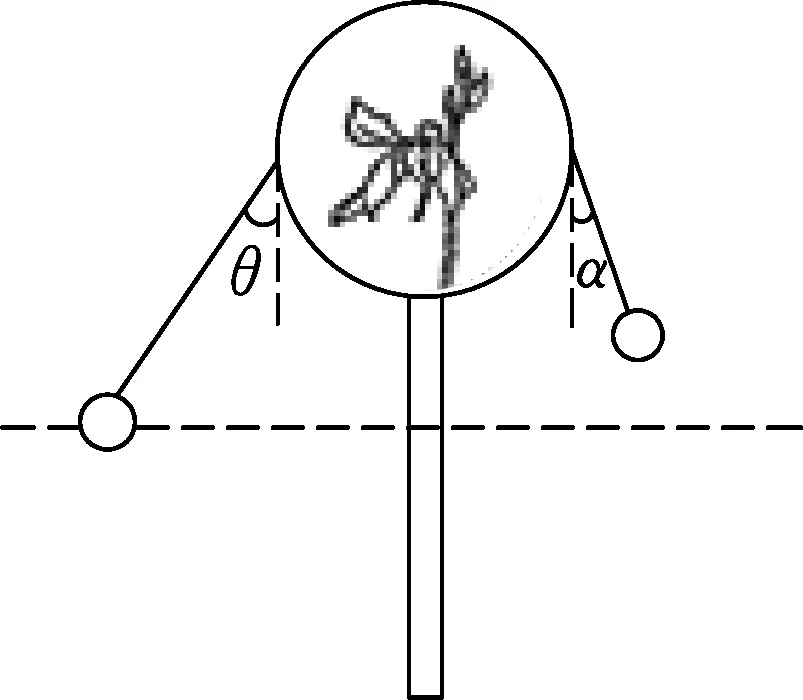
图3 拨浪鼓
重组场景2:“类”圆锥摆模型.
场景支持可以将视域放得更大,根据学生已有的经验踩准起点,因势利导让学生围绕有过亲历和接触的物理模型信息来完成场景的初建,引导学生主动展开推理、分析和鉴别等活动,促成知识体系的自主搭建,从而让他们将个体原有的“隐性知识”转变为共性且科学的显性知识,将琐碎零散的原始物理问题抽象出相类似的物理模型.
例如,重组火车转弯(如图4)、飞机转弯(如图5)、双漏斗转球(如图6)等生活中常见的场景,引导学生在场景中分析其轨迹圆的圆平面和受力特征,将原有场景中积累的知识和经验延展并迁移,从“类圆锥摆模型”深刻认知“圆锥摆模型”.
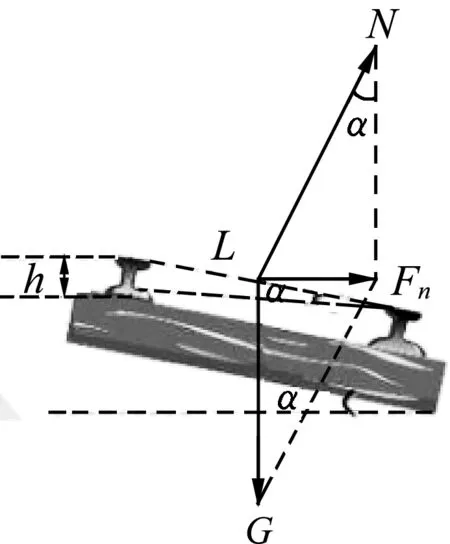
图4 火车转弯

图5 飞机转弯
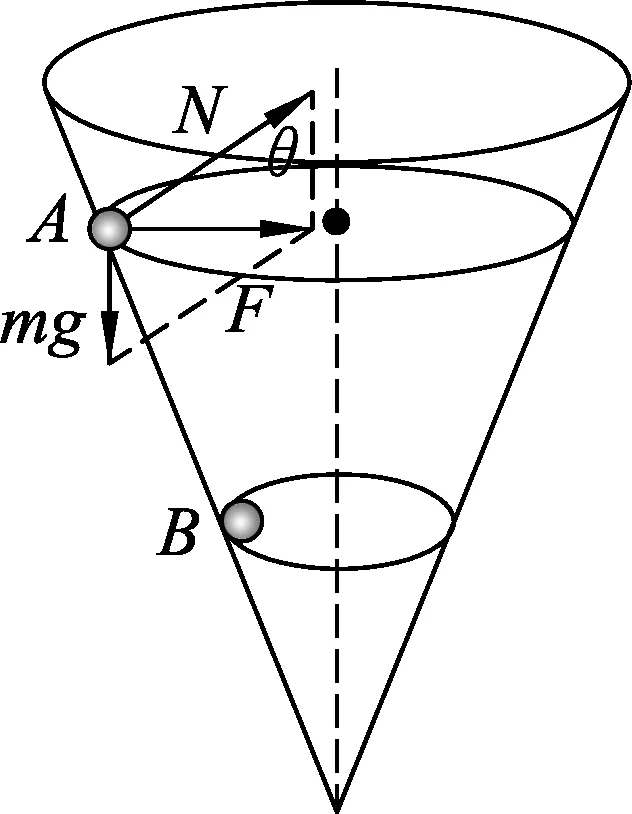
图6 双漏斗转球
如图4所示,火车转弯问题的常见设问是设计转弯确保车轮与轨道内、外侧向均没有挤压的时速和所垫高度问题.在教学过程中,还可以引导学生有意识的类比圆锥摆模型,轨道正面对火车的支持力N相当于圆锥摆模型(图1)中的拉力F,轨道与水平的夹角α相当于圆锥摆模型(图1)中的夹角θ.飞机在水平面内转弯的情境如图5所示,为了实现水平转弯,需要机翼倾斜(其本质与火车水平转弯一致),升力相当于图1中绳子拉力和图4中的支持力,机翼与水平面的夹角相当于图1中的夹角θ和图4中的夹角α.
图6中2个相同的小球沿着光滑漏斗壁做匀速圆周运动,我们对其中一个小球进行受力分析.支持力N相当于圆锥摆模型(图1)中的拉力F,漏斗壁与水平面的夹角相当于(图1)中的夹角θ,若进一步类比还可以得到等效摆线长的概念,这两个小球受到漏斗壁的支持力大小、运动周期大小存在着怎样的关系呢?如果类比圆锥摆,由于摆角相等,所以支持力大小相等,从圆锥摆的周期公式出发,悬点到圆平面的高度hA>hB,所以TA>TB.
正如钱学森所说:“在科学的研究里,最重要的一件事是怎样把理论和实际结合起来”.在高中物理学习阶段,建模就是将物理知识与生活情境相联系,教学中不仅要引导学生更为全面、深刻的认识物理模型,还应该通过情境的转化引导学生实现模型的类比、迁移与应用,唯有如此才能有效提升学生的建模能力和学科核心素养.此外,从当前的高考实际来看,新高考题量大、时间短,注重学生素养水平的考查,要求学生有较为敏锐思维,要能在较短的时间内将习题背景与物理模型相匹配.为此,我们在平时的物理教学中更应该注重教学的场景支持,借助场景帮助学生认识物理模型的本质,通过场景重组实现模型的迁移.开展这样的延展式教学,才能让学生内化知识、提升素养.

