把握数学表征特点，提升建模解决物理问题能力

陈林桥 贾苏荣

（1.江苏省扬中市教师发展中心，江苏 扬中 212200；2.江苏省扬中市第二高级中学，江苏 扬中 212200）

建构物理模型是一种研究物理问题的科学的思维方法.即在研究和解决物理问题时，忽略次要因素，抓住主要因素，并进行合理抽象概括，突出客观事物的本质特征，从而达到解决物理问题的目的.其中物理模型建构往往涉及到数学表征这一问题，因此明晰数学表征类型以及把握其特点和功用，将有助于提升我们正确建构模型解决物理问题的能力.

1 用“图”来表征解答问题

根据物理问题所给的条件和实际情况，运用几何图形、函数图像等形式进行恰当的表征，在明确几何图形、函数图像所表示的物理意义基础之上进行有效的分析，由此来解决物理问题.

1.1 基于几何图形表征求解

例1.火车以60m/s的速率转过一段弯道，某乘客发现放在桌面上的指南针在10s内匀速转过了约10°.在此10s时间内，火车

（A）运动路程为600m.

（B）加速度为0.

（C）角速度约为1r a d/s.

（D）转弯半径约为3.4k m.

解析：依据题意，不难画出反映题中火车运动的情境示意图图1来，火车在以O为圆心弯道上运行，指南针时刻指向地磁南极.

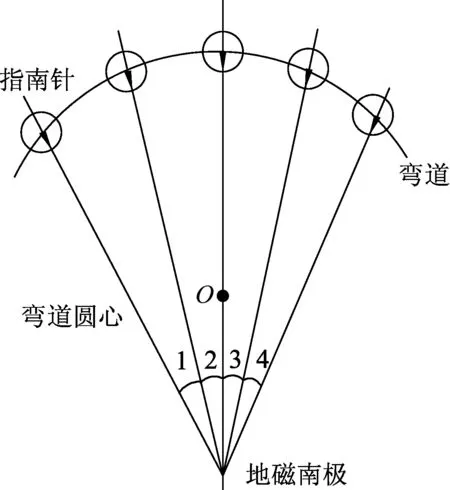
图1

题目给出车中“桌面上的指南针在10s内匀速转动”.这表明指南针在相同的时间内绕磁南极点转过的角度相同，即有图1中∠1=∠2=∠3=∠4.但鉴于弯道的圆心O与地磁南极不重合，所以在相等时间内运动的弧长却并不都相等，因此可以断定火车在严格意义上不是做的匀速圆周运动.然而考虑到火车运行的实际情况，研究的是非常短的10s时间内的情境，再有火车在弯道运行的区域相比地球大小而言要小得很多，所以地磁不均匀分布这一影响就可以忽略，那么由此就可以把弯道处的地磁场看作匀强磁场.于是我们就有理由认为指南针指针相对地面而言始终指向某一方向（与磁感线平行），指南针的底盘却随火车一起绕弯道圆心O做圆周运动，因此我们就可以建构起示意图2来表征本题的物理情境，并假设火车上的指南针从A位置沿弯道运动到B位置，火车相对于弯道圆心O转了α角，指南针的地盘相对于指针偏转了β角，那么由图可知，α角的两条边和β角的两条边相互垂直，根据数学知识，于是得到α=β.这就是说，指南针相对于地盘转过的角度始终等于火车相对弯道圆心O转过的角度，因此指南针指针相对于底座转到和火车在弯道转弯的角速度相同，于是得到10s时间内火车运动路程s=v t=60×10m=600m，选项（A）正确；火车在弯道上运动，做曲线运动，一定有加速度，选项（B）错误；火车匀速转过10°，约为角速度选项（C）错误；由v=ω R，可得转弯半径约为3.4k m，选项（D）正确.所以选（A）、（D）.

图2

说明：从以上解答中的数学表征的特点来看，主要是根据题目文字的描述，运用我们相关数学几何方面的知识，将试题问题情境用直观而又形象的几何图形来表征，并随着对试题认知的不断深入和解题的实际需要，又从“对图1否定“进而新建出“切合题意的图2”来，进而解决问题.可见，一个符合题意情境的几何图形表征的建构对问题的解答突破起到了关键的作用.

1.2 基于函数图像表征求解

例2.中欧班列在欧亚大陆开辟了“生命之路”，为国际抗疫贡献了中国力量.某运送防疫物资的班列由40节质量相等的车厢组成，在车头牵引下，列车沿平直轨道匀加速行驶时，第2节对第3节车厢的牵引力为F.若每节车厢所受摩擦力、空气阻力均相等，则倒数第3节对倒数第2节车厢的牵引力为

解析：设车头对后面车厢的牵引力为F总、每节车厢质量为m、受到的摩擦力和空气阻力的合力为f、第n节对后面车厢的牵引力为Fn、火车的加速度大小为a.因此，对于前面n节车厢而言，根据牛顿运动定律得到F总-Fn-n f=n ma，变形得到Fn=F总-n（f+ma），作出Fn和n的函数关系图像如图3所示.再根据图像中两个三角△a b c和△a e d相似关系得到倒数第3节对倒数第2节车厢的牵引力F′=所以选项（C）正确.

图3

说明：从以上解答中的数学表征的特点来看，主要是基于物理问题运用数学知识，找出Fn和n两者之间的函数关系式.这个关系式含有的未知数竟有4个之多，却不能直接有效地得到“倒数第3节对倒数第2节车厢的牵引力”的大小.于是我们根据这个关系式作出它们的函数图像，利用图像中三角形相似关系来解决这个问题.可见这里函数图像的表征恰恰是解答本题的核心所在.

2 用“式”来表征解答问题

在具体物理问题中找出物理量之间的数学关系式，结合数学自身的特征和规律，作出符合逻辑的推导或合理外推，在基于所得到的数学结果的基础上做出物理判断和解释，从而解决物理问题.

2.1 基于数学关系式演绎性表征求解

例3.在游乐节目中，选手需借助悬挂在高处的绳飞越到水面的浮台上，小明和小阳观看后对此进行了讨论如图4所示.他们将选手简化为质量m=60k g的质点，选手抓住绳由静止开始摆动，此时绳与竖直方向夹角α=53°，绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深.取重力加速度g=10m/s2.假如选手摆到最低点时松手，小明认为绳越长，在浮台上的落点距岸边越远；小阳却认为绳越短，落点距岸边越远，请通过推算说你的观点.

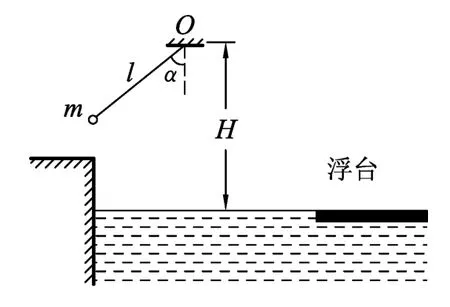
图4

解析：选手从开始摆到最低点过程中机械能守恒，则有

选手离开最低点做平抛运动，于是有

综合以上几式解得

因此，两人的看法均不正确，只有当绳长越接近1.5m时，落点距岸边越远.

说明：以上解答中的这种数学关系式演绎性表征的特点，就是基于对题目情境做具体的物理分析，从而建立起选手水平距离和绳长之间的函数关系式，然后运用数学函数极值的方法来确定这个问题的判断基点，进而做出相应的物理判断，整个解答过程简洁明了，很有说服力.

2.2 基于数学关系式归纳性表征求解

例4.雨滴在穿过云层的过程中，不断与漂浮在云层中的小水珠相遇并结合为一体，其质量逐渐增大.现将上述过程简化为沿 竖直方向的一系列碰撞.已知雨滴的初始质量为m0，初速度为v0，下降距离l后与静止的小水珠碰撞且合并，质量变为m1.此后每经过同样的距离l后，雨滴均与静止的小水珠碰撞且合并，质量依次变为m2、m3…mn…（设各质量为已知量）.不计空气阻力，求第n次碰撞后雨滴的动能.

解析：（1）第1种情境，若不计重力，则全过程中动量守恒，于是有m0v0=mnvn′，解得

所以得到第n次碰撞后雨滴的动能

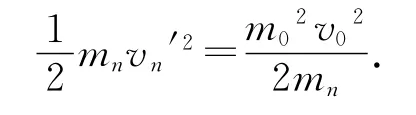
（2）第2种情境，若考虑重力，那么雨滴下降过程中做加速度为g的匀加速运动，碰撞瞬间动量守恒，则有，第1次碰撞前

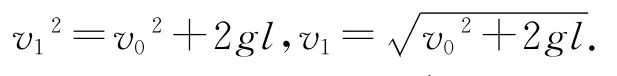
第1次碰撞后mv=mv′.解得

利用（1）式化简得

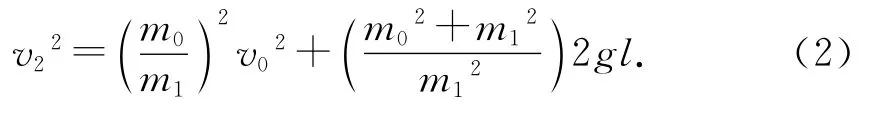
第2次碰撞后，由（2）式得

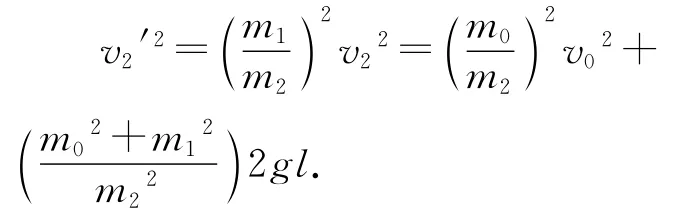
同理，第3次碰撞后

……

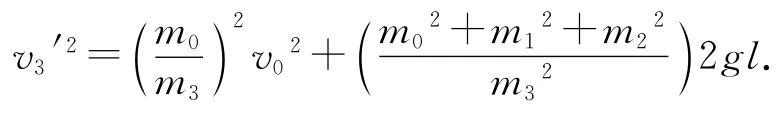
由此推得第n次碰撞后

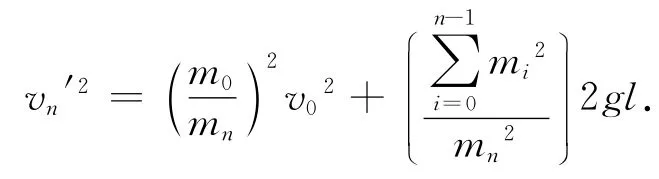
所以得到第n次碰撞后雨滴的动能

说明：本题第2种情境解答中的这种数学关系式归纳性表征的特点，就是基于物理问题情境运用物理规律和公式建构起物理量之间的基本关系式，然后利用数学中不完全归纳法的思想来进行合理的外推，即由相关物理知识求出雨点第1次、第2次以及第3次碰撞后速度表达式.仔细分析这些表达式的数学结构特征，对此进行合情合理外推得出第n次碰撞后的速度表达式，最终求得第n次碰撞后雨滴的动能.

通过以上几个具体实例解答的剖析，我们不难总结得到数学表征建模解题的一般思想方法，即对物理问题中的情境、结构以及要素等相关量及其之间的关系进行数学符号化的描述.在此基础上建构与之密切相关的而且有利于问题解决的几何图形、函数图像、数学关系式等较为抽象的数学“图”或“式”来表征分析物理问题，再根据数学知识的特点和规律进而有效地解决物理问题.