基于组合模型的江苏省居民用电量预测分析

王 琪

（南京财经大学 经济学院，江苏 南京210046）

根据江苏省统计局关于全社会用电量的报告，江苏省居民用电量是逐年增加的，与此同时民用电量占社会总用电量的比例也是逐年增加的。数据的变动说明了人民生活需求的提高，同时也表明对居民用电量的预测研究有着较大的经济意义。为了帮助电力行业适应这个发展新形势，本文以江苏省为例，尝试采用非组合模型与组合模型预测居民用电量，从而得出一个相对较优的预测模型。

一、预测方法

（一）季节性时间序列模型

季节性ARIMA(p,d,q)(P,D,Q)m，ARIMA(p,d,q)(P,D,Q)m的AR(p,d,q)(p,d,q)IMA模型是在ARIMA(P,D,Q)m(P,D,Q)m模型的基础上增添了代表季节性的项，可以写成为：ARIMA(p,d,q)(P，D,Q)m。其中(p,d,q)代表模型中的非季节部分，(P，D,Q)m代表模型中的季节部分，这里的m代表每年的观测数量。季节性的地方在模型中用大写英文字母表示，而不属于季节性的部分则用小写的英文字母表示。季节性与非季节性的分式中都具有相像的部分，但是季节性的项包含了季节性时段的回溯，可以通过R软件画出模型的PACF图和ACF图。从这两张图中观察出模型是否具有季节性特征。值得注意的是，在构建季节性ARIMA模型时要约束季节性延迟，从而得出最优的季节阶数。

（二）ETS模型

Error-Trend-Seasonality模型，简称EST模型，它由误差项、趋势项、季节项三个部分的任意组合构成。其中，误差项（Error）可以是相加模型或相乘模型趋势项（Trend）可以是无、相加模型、相乘模型；季节项（Seasonality）可以是无、相加模型、相乘模型。误差项为相加模型时，最大似然法等价于使SSE最小来进行参数估计。EST模型相较其他模型有一个可以进行模型选择的显著优势，即对于现有的时间序列，通过BIC、AIC和AICc这三个指标进行统计。

其中L是模型的似然函数，k是已估计的参数个数和初始状态的总和（包括残差的方差）。针对小样本偏差修正的AIC（AICc）可以写成：

（三）神经网络自回归模型

人工神经网络也可以对数据进行建模预测，可以简写为ANN，它的长处在于可以适用于解释变量与被解释变量存在复杂非线性关系的数据。针对本文的时间序列数据，ANN是将滞后值当成神经网络纳入模型，该模型是神经网络自回归或NNAR模型。首先，考虑包含一个隐藏层的前馈网络，式子NNAR（p,k）显现出p期滞后输入与k个节点存在与隐藏层中NNAR(p,0)模型相当于ARIMA(p,0,0)(P,0,0)模型。其次，考虑季节性数据，可以将同一季节的最后观测值纳入模型。NNAR(p,P,0)m模型相当于模型ARIMA(p,0,0)(P,0,0)m。

（四）评价指标

平均绝对误差（mean absolute error），又简称为MAE，它是预测值与真实值误差绝对值的平均数。之所以要加上绝对值，是因为如果误差是[1,0,-1]，则平均误差值就是0，但实际上预测值并不是完全等于真实值，它的定义表达式为：

均方根误差（root mean squared error），简称为RMSE，也称为RMSD。它是预测值和真实值误差平方平均值的平方根，能用来衡量误差的平均大小，它的定义为：

平均绝对百分比误差（Mean Absolute Percentage Error），简称为MAPE，定义如下：

二、实例分析

（一）数据来源以及预处理

本文选取2004年1月至2018年12月江苏省城乡居民用电量数据，来拟合不同的模型。由于某些特殊原因，在一些统计年鉴中并没有相应的月份统计数据，数据中存在一定的缺失值，故本文采取了组合补齐法，使用R中的imputeTS包进行缺失值填补。由于用电量月度数据具有一定的季节性，故采用季节性调整与线性插值法，此方法适用于具有趋势和季节性的数据。同时，利用R软件绘制出2004年到2018年的时间序列图，生成的时间序列图如图1的第一张图所示。

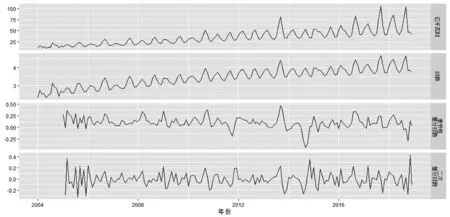
图1 数据处理对比

江苏省居民用电量在2004—2018年具有上升趋势并呈现出一定的季节波动性，数据显然是非平稳的。为了处理这种非平稳性，可以采用多种方法。本文为了使原始数据达到平稳时间序列的状态，分别采用了取对数、季节性差分、二次差分的方法。处理结果如图1所示，若只取对数，数据依旧呈现不平稳的状态。季节性差分与二次差分的效果相当，但是数据还是处于一点非平稳的状态。差分方式的选择没有客观的标准，故本文选择第三种差分方式。

（二）三种模型的预测结果

1.AIMRA模型的拟合。forecast包里的auto arima()函数，是专门用来进行季节性ARIMA建模的。把数据代入，模型为ARIMA(3,1,2)(2,1,1)。接着，对这个复杂季节性模型的残差进行检验，图2展现的就是检验的结果，残差几乎都在显著性临界值内，故判定这些残差类似于白噪声。与此同时，Ljung-Box检验的p值为0.9899，非常高，这就证明了该数据的残差之间不存在自相关性，序列的信息已经完全提取。

图2 残差自相关图

此时经过所有检验的模型就是本文所要构建的季节性的ARIMA预测模型。将其应用到对2018年江苏省城乡居民用电的预测中去，预测结果如图3所示。对于2018年江苏省城乡居民用电的预测值依旧顺应了之前的波动趋势。黑色线条代表原始序列，不同置信度下的预测区间通过不同深度的颜色显示。

图3 ARIMA、EST、NNAR模型预测图

2.ETS模型的拟合。最小化AICc是一种选择模型的方法，本文使用R语言中的ETS()函数来实现。图4展现了ETS模型的分解图，ETS模型的三个字母分别代表ETS(M,A,M)ETS(M,A,M)误差项、趋势项、季节项，可以由这三个部分任意搭配建模。如图4所示，最终拟合了模型，它是具有乘性误差、加性趋势和乘法季节性的方法。对于夏季制冷、冬季制热这种家庭用电高峰期会使得居民用电量呈现一种季节振幅，而ETS模型恰好可以预测这种有周期性变化的数据。图4中展现了EST模型对2018年江苏省城乡居民用电的预测结果。

3.神经网络自回归模型的拟合。使用R语言中的nnetar()函数来拟合神经网络自回归模型。该模型的预测变量是最后12个月的用电量，4个神经元存在于隐藏层中。用电量的季节性被此模型很好地拟合了。与本文中所讨论的大多数方法不同，神经网络不是基于明确定义的随机模型，因此也不能直接得到预测值对应的预测区间。但是，仍然可以使用模拟来得到预测区间，在模拟过程中，通过bootstrap残差项生成未来的样本路径。预测如图4所示。

图4 ETS模型的分解图

4.组合模型的拟合。本文分别建立ARIMA模型、ETS模型和神经网络自回归模型对2004年到2018年江苏省居民用电量数据进行分析，并且对比分析了不同模型的预测效果。结果表明，3个模型全部有效。将多个单一的预测模型通过适当的方法整合，就可以建立出一个组合模型。组合模型就是多个不同模型，通过适当的加权平均等方法，得到一个全新的模型。组合模型是集多个模型的优势于一身，填补各个模型的缺失处，使得最终的预测效果更贴合实际。故本文将上述三个模型构建在一起，建立一个能够提升预测效果的组合模型。

用ω1表示ARIMA模型的权重系数，用ω2表示ETS模型的权重系数，用ω3表示NNAR模型的权重系数。单个模型的权重分配是组合模型能否高效的重点，本文采取了两种方法来计算权重。组合一是等权平均法，ω1=ω2=ω3。组合二是均方误差倒数法，算得ω1=0.3054，ω2=0.2462，ω3=0.4484。

（三）五组模型的对比

表1列出了五种组合模型的预测值，尽管最终的预测值都不一致，但根据表2所示的模型评价指标，这五种模型的预测结果都是有效的。首先，对比三个单一模型，预测效果依次由ETS模型、SARIMA模型、NNAR模型递增。其次，对比两个组合模型，组合二的效果略优于组合一，即对于本研究的组合模型而言，分配权重采用等权平均法要略优于均方误差倒数法。最后对比单一模型与组合模型，发现组合模型所体现的性能要明显优于所有的单一模型（见表1、2）。

表1 五种模型预测值

表2 五种模型评价

三、总结

组合模型目前已经得到了较为普遍的运用，它能够使得预测值更接近于真实值。并且在时间序列数据的预测中，组合模型能够克服对时间的敏感度，无论是长期预测还是短期预测都能有较高的精度。

对于本研究而言，加权系数构成的模型就是相对最优的预测模型。在此基础上，可以对未来的江苏省居民用电量进行预测，以便相关产业调整自己的产能计划。然而组合模型的权重系数也是影响预测精度的重要因素之一，权重系数的选择并不是一成不变的，具体使用哪种权重系数的组合预测模型才是最优的，还需要对具体问题具体分析。构建出最优的预测模型才能使预测的结果更贴合实际，才能为决策者们提供有效信息，才能使预测更有经济意义。