基于多适应度量子遗传算法的X射线荧光重叠峰分解

汪雪元，何剑锋*，聂逢君，袁兆林，刘 琳

1.东华理工大学江西省放射性地学大数据技术工程实验室，江西 南昌 330013 2.东华理工大学江西省核地学数据科学与系统工程技术研究中心，江西 南昌 330013 3.东华理工大学软件学院，江西 南昌 330013

引 言

在复杂地质样品的X射线荧光分析中，峰位接近的谱峰之间常常会发生重叠，严重的重叠谱峰对于样品成分定性分析的准确度和定量分析的精度构成较大影响。重叠峰分解一直是光谱分析领域的重点研究课题，遗传算法和人工神经网络等智能算法近年来被广泛应用于光谱重叠峰分解[1-6]。黄洪全等提出了高斯混合模型结合期望最大化迭代算法进行重叠峰分解[7]；杨熙等将粒子群算法应用于重叠谱峰的解析[1]；黄凡等将模拟退火算法应用于振动光谱成分分析[2]；徐喜荣[4]等将神经网络分析应用于重叠峰的分解。智能算法在对谱峰重叠严重的复杂地质样品进行分析时，往往存在计算量过大、弱峰误差较大、收敛于局部极小值或不收敛等问题。

量子遗传算法具有较好收敛性，本文对量子遗传算法进行了改进。并将改进后算法和特征X射线谱的概率统计模型，应用于X射线荧光重叠峰的分解。实验结果显示，新方法提高了重叠峰分解的准确度。

1 原理与算法

1.1 GMM-EB模型

在X射线荧光能谱分析中，K系和L系特征X射线常分别用于轻元素和重元素的定性定量分析。K系谱线有Kα1，Kα2，Kβ1，Kβ2四条，L系谱线主要有Lα1，Lα2，Lβ1，Lβ2，Lγ1五条。将元素的K系和L系特征X射线应用于能谱分析，有助于提高元素定性分析的准确度和定量分析的精度。因此，提出了一种基于X荧光分析仪分析范围内的所有元素的元素关联高斯混合模型(gaussian mixture model-element related，GMM-ER)

(1)

式(1)中，M为X荧光分析仪能识别的元素数量。T(i)为元素i的特征X射线条数，α(i,j)为元素i的第j条分支谱线的权重，且满足式(2)。

(2)

式(2)中，u(i,j)和σ(i,j)分别为元素i的第j条分支谱线的均值和标准差。u(i,j)和元素的对应射线能量相关联,是线性关系；并且，σ(i,j)和u(i,j)之间存在线性关系[1]，即有σ(i,j)=u(i,j)σ(1,1)/u(1,1)(i=1,…,M；j=1,…,T(i))。对于K系特征X射线，除少量轻元素外，α(i,1)，α(i,2)，α(i,3)，α(i,4)之间的比值是确定的。GMM-ER模型的参数可表示为θ=[α(1,1)，α(1,2)，…,α(1,T(1)),…,α(M,1)，α(M,2),…,α(M,T(M))，u(1,1)，u(1,2)，…,u(1,T(1)),…,u(M,1)，u(M,2),…,u(M,T(M))，σ(1,1)，σ(1,2)，…,σ(1,T(1)),…,σ(M,1)，σ(M,2),…,σ(M,T(M))]。

1.2 GMM-EB模型的参数估计

设样本数据为x(n)(n=1,2,3,…,N)，n为道址，x(n)为道址n处的计数值。可以采用期望最大化法(expectation maximization，EM)的迭代算法由样本数据求得GMM-ER模型的参数θ值。在实际求解过程中，由于GMM-ER模型的参数太多，θ的求解经常难以实现。本文通过下面方法实现对θ的简化。

1.3 GMM-EB参数的改进量子遗传算法估计

量子遗传算法(quantum genetic algorithm,QGA)基于量子计算原理，对参数采用量子比特编码，利用量子逻辑门实现染色体的演化。相对于常规遗传算法，量子遗传算法常常可以获得较好的收敛性[8-10]。为减少计算量和演化迭代次数，本文根据光谱数据特点对传统量子遗传算法进行改进。

(3)

式(3)中，k为编码每一位基因的量子比特数，e(d)为第d光谱段待分析元素数量，且有|αij|2+|βij|2=1。

(4)

(5)

(3)量子旋转门：量子遗传算法通常采用量子旋转门实现演化操作，如式(6)所示，其中θi为旋转角。

(6)

(4)初始化群体：在改进量子遗传算法中，由式(7)得到a(i，1)的初始值，其中，cu(i，1)表示道址u(i，1)处的相对计数值。由a(i，1)确定个体量子比特编码初始值。

(7)

2 重叠谱峰解析

2.1 模拟重叠谱生成

用高斯函数模拟能量色散X荧光谱线特征峰，产生原子序数25—28元素锰、铁、钴和镍的模拟光谱。这四种元素的主要K系特征X射线能量及比例关系如表1所示。

表1 锰、铁、钴和镍的主要K系特征X射线Table 1 Main K-series characteristic X-rays of Mn,Fe,Co and Ni

假设一2 048道的能量色散X荧光分析仪的能量刻度已知，其能量E和道址N的关系式如式(8)所示

E=0.007 955N+0.134 714 (keV)

(8)

则由式(8)可求得GMM-ER模型中元素锰、铁、钴和镍的u(i,j)的值。设σu值已知为0.04，则由σ(i,j)=u(i,j)σu可求得σ(i,j)的值，如表2所示

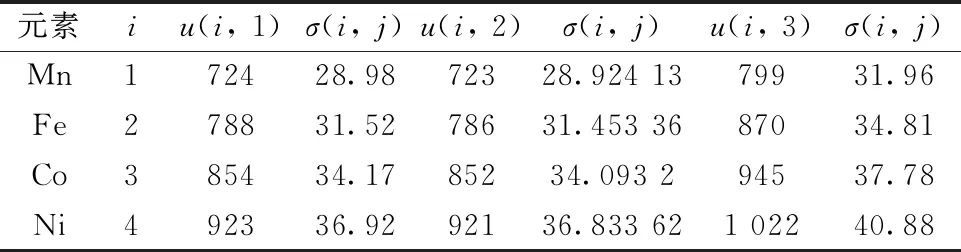
表2 锰、铁、钴和镍的u(i,j)值和σ(i,j)值Table 2 u(i,j)and σ(i,j)values of Mn,Fe,Co and Ni

锰、铁、钴和镍的模拟高斯特征峰(Kα1)的强度(峰面积)分别设为20 000，30 000，30 000和20 000。则模拟重叠谱如图1所示。可以看出，谱峰重叠严重。

图1 锰、铁、钴和镍的模拟重叠谱Fig.1 Simulated overlapping spectra of Mn,Fe,Co and Ni

2.2 重叠谱峰分解

采用传统量子遗传算法和改进的量子遗传算法的群体搜索技术，计算在统计意义下形成重叠谱的随机数归属于各个GMM-ER模型的概率，搜索到“全局最大概率”GMM-ER模型，该GMM-ER的参数就是所求元素Kα1或Lα1特性X射线的强度。

(1)确定GMM-ER模型参数

(3)重叠峰分解及总体结果分析

设置初始种群个体为100，迭代次数为100。将传统量子遗传算法和改进量子遗传算法分别应用于模拟重叠谱的分解。每种算法进行10次分解，分解过程的最优适应度值如表3所示。最优适应度值越小表示总体误差越小，即重叠峰分解效果越好。

表3 重叠谱分解的最优适应度值Table 3 Optimal fitness values of overlapping spectral decomposition

从表3结果计算可得，最优适应度平均值降了32.1%，改进量子遗传算法的重叠峰分解效果总体优于传统量子遗传算法。传统量子遗传算法第7次实验的分解效果最佳，最优适应度值为13 833，改进量子遗传算法第5次实验的分解效果最佳，最优适应度值为3 604，最优适应度值降了73.9%，可以看出，在最佳重叠峰分解效果方面，改进量子遗传算法远远优于传统量子遗传算法。

(4)最佳分解效果分析

对两种遗传算法的最佳重叠峰分解效果进行比较。传统量子遗传算法第7次实验和改进量子遗传算法第5次实验的重叠谱分解情况如图2和表4所示。

从图2可以看出两种量子遗传算法均能成功分解重叠谱峰，且GMM-ER重叠峰和原始重叠谱均能较好拟合。但从表4可以看出，除铬、铁外，锰、钴、镍、铜和锌的分解相对误差，改进量子遗传算法优于传统量子遗传算法。在应用量子遗传算法对重叠峰进行分解的过程中，含量比例高的元素对总体分解精度的影响大于含量比例低的元素。在只有一个适应度值的传统量子遗传算法中，含量比例高的元素会获得最优分解效果，而含量比例较低的元素的分解精度可能较差。而改进量子遗传算法对每一种待分解元素都设有一个适应度值，使得不同含量比例的元素的分解精度较为均衡。表4中，传统量子遗传算法的分解相对误差区间为[-3.19，2.35]，改进量子遗传算法为[-0.815，1.15]，缩小了64.5%。可以看出，改进量子遗传算法的分解精度总体上高于传统量子遗传算法。

图2 原始重叠谱、GMM-ER重叠峰和分解峰(a)：传统量子遗传算法；(b)：改进量子遗传算法Fig.2 Original overlapping spectrum,GMM-ER overlapping peak and decomposition peak(a)：Traditional quantum genetic algorithm；(b)：Improved quantum genetic algorithm

表4 分解前和分解后的特征X射线强度Table 4 Intensity of characteristic X-ray before and after decomposition

图3为传统量子遗传算法和改进量子遗传算法运行过程中全局最优个体的适应度值随迭代次数变化趋势图。可见，改进量子遗传算法的收敛速度快于传统量子遗传算法。

图3 搜索全局最优GMM-ER的过程(a)：传统量子遗传算法；(b)：改进量子遗传算法Fig.3 The process of searching global optimal GMM-ER(a)：Traditional quantum genetic algorithm；(b)：Improved quantum genetic algorithm

3 结 论

由元素的K系和L系特征X射线，从统计学角度提出了一种基于X荧光分析仪分析范围内所有元素的元素关联高斯混合模型(GMM-ER)。并基于X射线荧光光谱的物理特性和GMM-ER模型的特点，对传统量子遗传算法进行了改进。用传统量子遗传算法和改进量子遗传算法对模拟重叠谱进行重叠峰分解。实验结果显示，改进量子遗传算法的重叠峰分解精度优于传统量子遗传算法，并且收敛速度快于传统量子遗传算法，且相对误差曲线更为平滑。通过对一铅黄铜标样(Cu:62.83%,Zn:33.56%,Pb:2.30%,Fe:0.16%,Sn:0.33%,Ni:0.31%,Mn:0.12%)的实验光谱进行分析，采用本文的改进量子遗传算法进行重叠峰分解，其效果优于传统量子遗传算法。综上所述，本文提出的基于元素关联高斯混合模型和改进量子遗传算法的谱线解析方法，特别适合于严重的重叠谱峰的分解。