激光在准球形边界卷云中传输的衰减和透过特性

任神河，高 明，王明军，李 艳，郭镭力

1.西安工业大学光电工程学院，陕西 西安 710021 2.咸阳师范学院与中国科学院近代物理研究所联合共建：离子束与光物理实验室,陕西 咸阳 712000 3.西安理工大学自动化学院，陕西 西安 710048

引 言

激光在卷层云、卷云等复杂介质中的传输与散射研究自20世纪50年代起一直倍受学者关注，在各个国家国防、军事航天及民用领域都具有较强的学术价值和应用背景。由于高空卷云的散射和吸收特性，云层对激光传输有显著影响[1]，使得地空链路上激光传输信息能力减弱，降低通信质量。研究卷云对激光辐射传输的影响，对于激光通信、激光探测和激光遥感等都有重要意义。激光在卷云中传输有两种物理过程，第一种为直接透射，即激光直接经过卷云透射的传输过程；第二种为激光在卷云中多次散射，即激光经过卷云冰晶粒子多次散射后透射的传输过程。

近年来，国内外学者开展激光在云层的辐射传输特性研究，其中，2015年陈卫等[2]根据云层的粒子尺度分布，采用Mie理论数值计算了水云模型的激光散射特性；2016年Emde C等[3]采用Mie理论数值计算了水云的平均消光效率和相函数特性；2020年陈杰等[4]结合实验观测的空气质量数据，对复杂卷云环境气溶胶粒子的光吸收效率作了对比分析；Liou等在考虑云层的多次散射时，在连续散射方法的基础上，建立了薄卷云的近红外机载激光传输模型；上述研究都是考虑平面平行的情况。研究表明，当云层覆盖的范围较大时，星地激光在有云大气中传输时就必须考虑地球曲率，即在模拟计算中将云层的边界假定为球形边界,虽然Rozanov[5]等以准球面模式为基础，开发的combined differential-integral approach involving the Picard iterative approximation(CDIPI)迭代近似能近似得到球形大气模式下辐射传输方程的解，但他们未系统地分析准球面模式下卷云大气激光传输的反射率和透过率特性。

本工作根据卷云中粒子的分布特征和卷云对激光的散射特性，结合球形边界云层的辐射传输理论，讨论在地球曲率影响下，激光在球形边界云层的直接衰减特性和多次散射特性,计算了三种激光波长在卷云中的直接衰减特性。然后在考虑多次散射情况下，给出了卷云的光学厚度、有效半径、相对方位角、卷云散射模型和观测角对激光传输透过率的影响。

1 球形边界冰晶粒子云层辐射传输理论

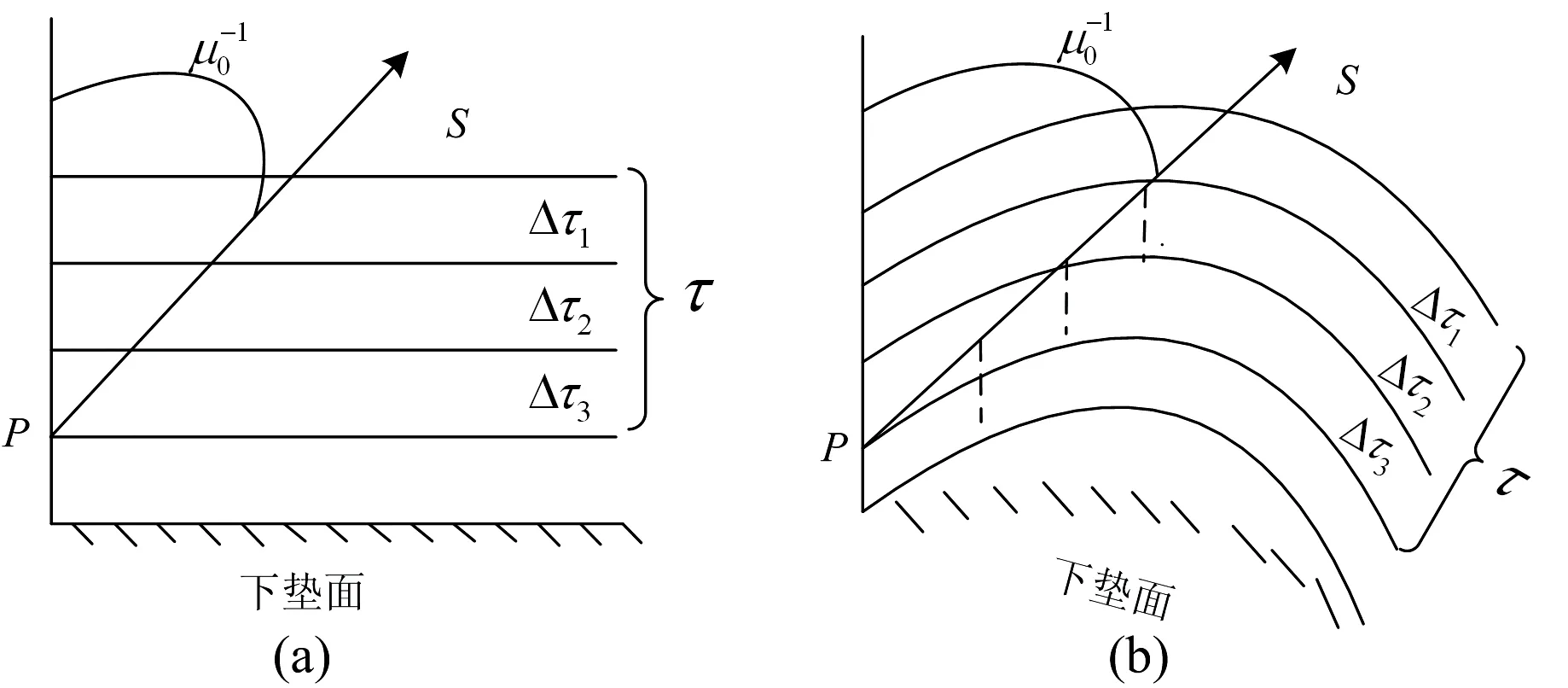
图1 平面平行边界大气与球形边界大气(a)：平行边界冰晶粒子云层；(b)：球形边界冰晶粒子云层Fig.1 Plane parallel boundary atmosphere and spherical boundary atmosphere(a)：Parallel boundary ice crystal particle clouds； (b)：Spherical boundary ice crystal particle clouds

建立考虑地球曲率时的准球面辐射传输方程，利用球坐标系进行分析，空间微分算子n·可表示为[6]

(1)

式(1)中，nr，nZ0，nA0分别为球坐标系中三个方向上的单位矢量，根据极坐标系中的方向余弦变换得到

(2)

式(2)中，Z0和Z是天顶角，ΔA是球坐标系中的相对方位角，求解辐射传输方程需用相对当地天顶的极坐标系，因此辐射强度I的导数由原平面坐标中的一个变量的函数转换成四个变量(θ，θ0，Δφ，n·)的函数。这时可将空间微分算子n·表示为[6-7]

(3)

图2中球坐标系是关于太阳和地心、以及关于天顶角和地心的，他可以与平行系统相比，前者涉及Z0和Z以及方位角之差ΔA，后者涉及天顶角θ0和θ以及方位角之差Δφ。θ0是与立体角n0有关的太阳天顶角，θ是与立体角n0有关的出射角，考虑到球体中一系列角度的几何关系，可求得变量间的数学关系

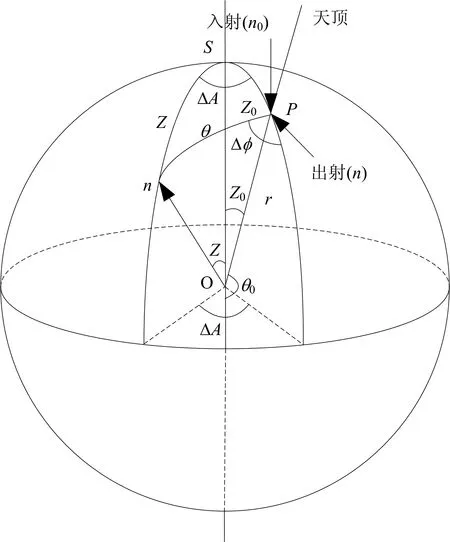
图2 空间微分算子示意图Fig.2 Schematic diagram of spatial differential operator

(4)

(5)

(6)

(7)

式中ds表示空间中相对当地天顶方向r上的微分距离。由式(4)至式(7)经过变换和运算，空间微分算子n·重新表示为

(8)

由式(8)可以看出：微分算子的最简形式是仅保留微分算子的第一项，但是分析地球曲率的作用时，需保留所有项。在平行大气中，将平面坐标下微分算子代入不施加坐标系的一般辐射传输方程，得到平面平行大气下的辐射传输方程。

将式(8)代入到一般辐射传方程中，可得球形边界条件下的辐射传输方程

n·I(r,μ,φ,μ0)=-β(r)[I(r,μ,φ,μ0)-

J(r,μ,φ,μ0)]

(9)

式(9)中，r是距地心的距离，源函数J(r,μ,φ,μ0)为

J(r,μ,φ,μ0)

(10)

式(10)中，ϖ为单次散射反照率；F0是大气层顶处入射光的辐照度；P(μ,φ;μ′,φ′)为散射相函数，它是散射角Θ的函数；(μ′,φ′)为入射光的空间位置，(μ,φ)为观测点的空间位置。式(10)中右侧第一项由多次散射引起，右侧第二项由单次散射引起；Ch(r,μ0)是Chapman函数，因此，exp(-Ch(r,μ0))表示为入射光的辐照度(光强)沿太阳光束路径上的衰减。

当太阳天顶角小于90°时，可以利用式(8)的第一项来近似计算平均辐射强度。因此空间微分算子n·可简化为[7]

(11)

这种简化近似就是准球形近似(pseudo-spherical approximation)。在平面平行中求解多次散射并在球形模型中校正直射光分量，即采用扰动技术用一系列平面平行模式下的辐射传输问题近似表示球形辐射传输方程。

将平面平行模式中的直射光分量Idir(τ,μ0)=F0exp(-τ/μ0)校正为适用于准球形模式中直接传输的光分量，即将源函数中的F0exp(-τ/μ0)改写为F0exp(-Ch(r,μ0))，这样就得到了准球形模式下的辐射传输方程

(12)

在准球形模式的辐射传输方程的基础上,可采用离散纵坐标的思想研究准球形模式的辐射传输过程,该过程的实施方法可参考Dahlback等开发的(DISORT)球面模式求解[8-9,3]。

2 结果与讨论

2.1 卷云层对激光辐射传输的直接衰减

当激光在地空链路传输时，不考虑多次散射，单次散射近似下激光在云层造成的直接透过率为[10]

T=exp(-Ch(r,μ0))=Ch(τ,μ0)

(13)

式(13)中，τ和μ0分别为卷云的垂直光学厚度和激光的入射天顶角。

在地空链路计算中，利用取对数形式得到激光链路在云层的直接衰减为

D=-10log[exp(-Ch(r，μ0))]

(14)

由图3可知，不管是波长的变化，还是有效半径的变化，随着传输距离增大，即光学厚度增加，激光在卷云中的衰减是逐渐增大的。文献[11]研究表明：水云大气的激光透过率随光学厚度增加，先线性增加后呈递减趋势，说明随着光学厚度增加，衰减也是增大的，本研究结果与文献[11]吻合。

图3 卷云对地空链路激光的直接衰减(a)：不同波长激光入射的直接衰减； (b)：不同有效半径下激光入射的直接衰减Fig.3 Direct attenuation of laser beam through cirrus cloud for air-to-ground communication link(a)：Direct attenuation of the laser at different wavelengths； (b)：Direct laser attenuation at different effective radius

2.2 基于多重散射的球形边界卷云透过率特性

光学厚度足够大时，激光在卷云中传输的多次散射必须求解辐射传输方程，根据球形边界卷云的辐射传输原理，利用离散纵坐标方法求解辐射传输方程。将大气分成多个不同的均质薄层，在各个均质薄层计算光学厚度、冰水含量和相对方位角等因素条件下的辐射传输方程组。在此，主要从卷云的有效半径reff以及冰水路径(IWP)/冰水含量(IWC)来定义冰云的物理性质，各参量的关系表示如式(15)

(15)

式(15)中，〈Qext〉为平均消光效率。Δz表示卷云的厚度,卷云大气的辐射传输特性用透过率(Transmittance)来表征，定义为[5,10-11]

(16)

式(16)中，μ0和μ分别为激光入射的天顶角和观测天顶角的余弦,It(τ,μ,φ)为在观测方向(μ,φ)激光透过云层的辐射强度，φ0和φ分别为入射方位角和观测方位角。

2.2.1 激光在平面平行模式和球形模式下卷云的透过率

讨论球形大气卷云的辐射传输特性，以0.65和1.06 μm激光入射为例，因为0.65 μm常用作为激光通信波长，1.06 μm常用作激光雷达探测、遥感探测的中心波段。结合CDISORT的平面平行边界模式和球面边界模式，表1、表2分别计算了不同入射天顶角下卷云大气激光传输的透过率。表1卷云的光学厚度τ取5，有效半径reff取10 μm；表2光学厚度τ取2，有效半径reff取40 μm。(由于透过率数值较小，表中为乘以1 000后的数值)。

表1 当μ为-1时，不同太阳天顶角下卷云大气透过率(τ=5，reff=10 μm)Table 1 The atmospheric transmittance of cirrus under different solar zenith angles for μ=-1(τ=5，reff=10 μm)

表2 当μ为-1，不同太阳天顶角下卷云大气透过率(τ=2，reff=40 μm)Table 2 The atmospheric transmittance of cirrus under different solar zenith angles for μ=-1(τ=2，reff=40 μm)

结合表1和表2分析可知：(1)较大天顶角入射(大于80°)时，球形大气模式下卷云的激光传输透过率大于平面平行模式，0.65 μm波长入射时卷云大气激光传输透过率的相对误差大于1.06 μm波长时的误差；(2)天顶角小于80°时两种大气模式下透过率的相对误差较小，随着天顶角的增大，两种大气模式下透过率的相对误差明显增大，天顶角为88°时0.65 μm波长入射时卷云大气激光传输的透过率误差达到69.09%。在卷云等复杂大气环境下，大天顶角入射时的遥感探测和激光通信都应该考虑球形边界。这里的结果是我们团队在文献[12]基础上所做的工作。文献[12]给出两种大气模式下卷云和水云大气激光传输的反射率差异。研究结果都表明：较大天顶角(大于80°)入射时两种大气模式下卷云大气激光传输的透过率和反射率的相对误差都明显增大。

2.2.2 激光在球形边界卷云的透过率特性

考虑球形边界卷云和多次散射，模拟计算三种激光波长以2°高度角入射球形边界卷云时，卷云的光学厚度、有效半径、相对方位角和卷云的冰晶模型对典型激光波长透过率的影响，太阳天顶角的余弦取μ0=cos(85°)=0.087 2，相关参量：大气廓线取美国标准大气，采用逐线积分法计算大气分子吸收，云底高度hb取9 km，云的几何厚度Δz取1 km，地表反照率取0，相对方位角φ-φ0取180°，探测高度为大气层底。

图4给出了三种波长下激光透过率随卷云光学厚度的变化关系。光学厚度较小时，由于透过卷云的光子来自云内粒子的多次散射效应，激光透过率几乎随光学厚度增加呈线性增大，当光学厚度增加到0.3附近时，随卷云光学厚度的增加使透过云层的光子数减少，因此激光透过率逐渐减少。但对于0.65和1.06 μm波长，其衰减主要是由于云层的散射特性影响。而对于3.8 μm波长，当光学厚度达到一定值后，吸收效率的增加使透过率衰减到0值附近。文中图4的结果和文献[11]的变化是一致的。

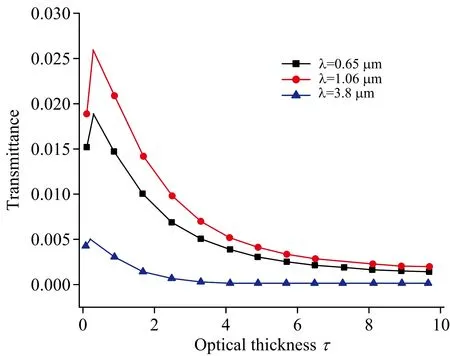
图4 卷云的光学厚度对激光透过率的影响Fig.4 Influence of optical thickness of cirrus cloud on laser transmittance

图5给出三种波长时，激光透过率随卷云粒子有效半径的变化关系。由图5可知，对于0.65和1.06 μm波长激光随粒子有效半径的增加激光透过率增加。这是由于粒子尺寸越大卷云的总消光效率越小，而且考虑多重散射时，粒子尺寸越大前向散射越强，则激光的透过率越大。对于3.8 μm激光随粒子有效半径的增加激光透过率减少，这由于在3.8 μm激光在卷云中有较强的吸收，且随有效半径的增加吸收逐渐增加，吸收效率的最大值接近45%，因此使激光在卷云中的衰减速度加快。文献[11]研究表明：当波长小于1 400 nm时，水云透过率随有效半径的增大而增大，当波长大于2 100 nm时，水云大气的透过率随有效半径的增大而减小，文中图5的研究结果与文献[11]结果基本吻合，只是文献[11]研究的是水云模型。

图5 卷云的有效半径对激光透过率的影响Fig.5 Influence of cirrus effective radius on laser transmittance

图6给出卷云的1.06 μm激光透过率在不同相对方位角时随观测角的变化关系。由图6可知，不同相对方位角时卷云的1.06 μm激光透过率随观测角的变化趋势差异较大，且随相对方位角的增加透过率减少，这是由于激光的入射高度角为2°时，0°—80°观测角在0°，90°，180°相对方位角时分别对应8°—88°，88°—89°，88°—168°散射角，8°—88°散射角时卷云有很强的前向散射，因此0°相对方位角的激光透过率最大。由散射角与辐射方向之间的关系式[13]

图6 不同相对方位角时卷云的激光透过率随观测角的变化关系Fig.6 Relationship between the laser transmittance of cirrus cloud and the view Angle at different relative azimuth angles

可知，0°相对方位角的激光透过率曲线在42°和66°观测角时取得极大值，它们分别与相函数的46°和22°散射峰值对应。并且相对方位角为0°时由观测角与散射角的对应关系可知，当观测角在0°—80°变化时，正对应于散射角从88°变化到8°，8°—88°散射角范围内对应于卷云相位函数的值是先增加到46°峰值，然后逐渐减少后又增大到22°峰值，最后再逐渐减少，与卷云的激光透过率的值是先增加到42°峰值，然后逐渐减少后又增大到66°的最大值，最后再逐渐减少，前后对应。

1.06 μm波长激光入射，不同散射模型的激光透过率随观测角的变化如图7所示：不同卷云散射模型的1.06 μm激光透过率随观测角的变化趋势差异较大，实心柱、聚合物和子弹玫瑰卷云散射模型在22°和46°散射角处都存在极值，因此卷云的激光透过率在66°和42°观测角附近出现极值。空心柱卷云散射模型只在22°散射角存在极值，因此卷云的激光透过率也只在66°观测角附近出现极值，而42°观测角附近曲线较为光滑。结果和文献[14]的水云模型做对比可以看出：不同卷云散射模型的变化趋势一致，但模型之间有差异，不同卷云散射模型对激光透过率的影响较大，在实际应用中需选择尽可能合理的散射模型。

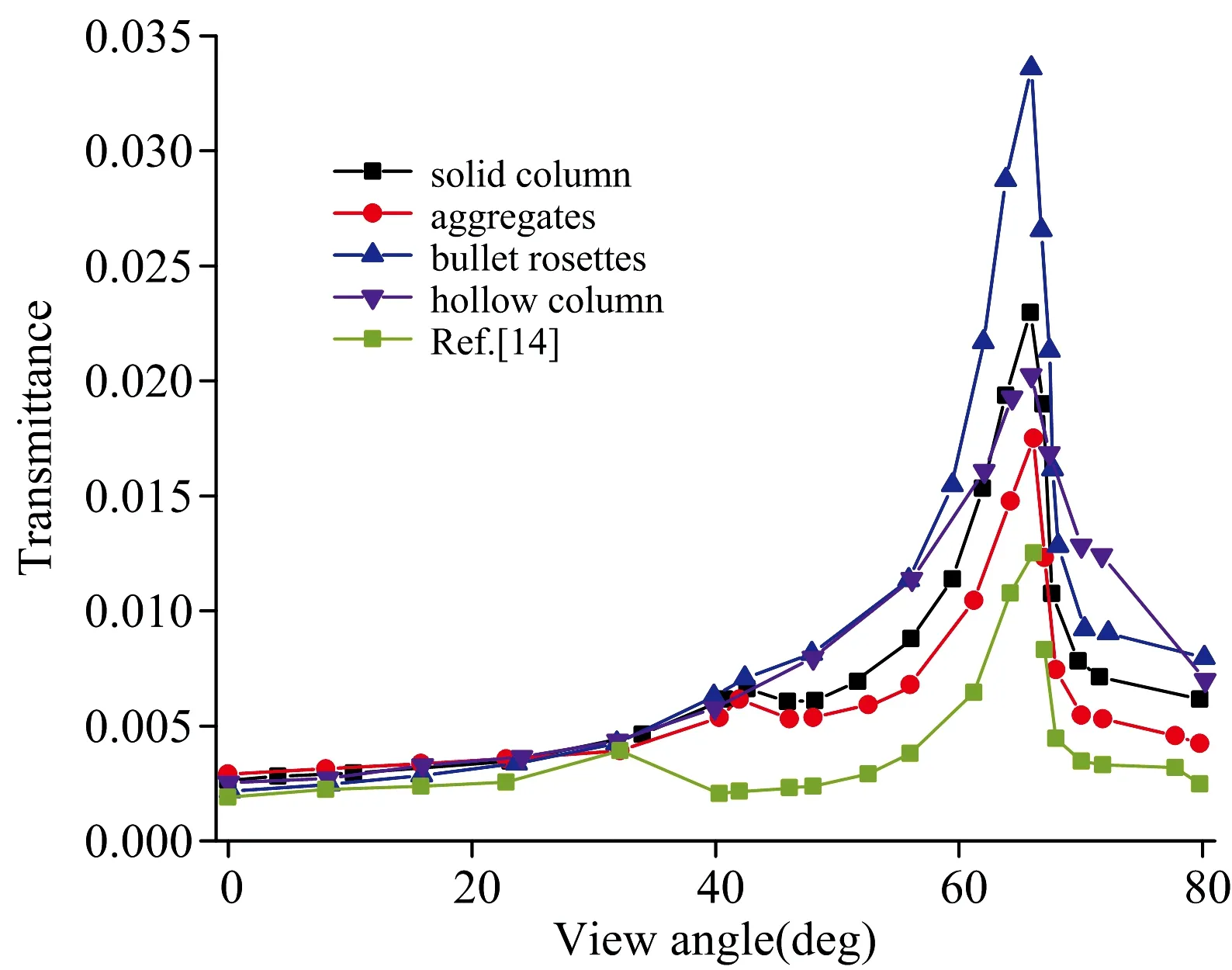
图7 不同卷云散射模型的激光透过率随观测角的变化关系Fig.7 Relationship between laser transmittance and view Angle for different models

3 结 论

根据卷云的分布特征和散射特征，计算了三种激光波长在卷云中的直接衰减特性，然后在考虑多次散射特性时，采用离散纵坐标法模拟计算了球形边界卷云的光学厚度、有效半径、不同相对方位角、卷云的散射模型和观测角对卷云的激光透过率的影响。结果表明：

(1)通过数值比较，验证了较小太阳天顶角(小于80°)入射时，CDISORT准球面模式下激光传输透过率的计算结果是合理的；较大天顶角入射(大于80°)时，两种模式下卷云大气激光传输透过率之间的差异随太阳天顶角的增大而增大，如果按照平面平行大气的假设计算辐射传输方程，0.65 μm激光波长在两种模式下的相对误差达到69%，因此必须考虑地球曲率对云层边界的影响。

(2)激光直接透过率与激光波长和卷云的厚度有关，随云层厚度的增加，激光在云层的传输路径增加，导致激光的衰减增强，随有效半径的增加卷云的总消光逐渐减小，导致激光的衰减减弱。

(3)球形边界卷云的散射和吸收特性共同影响激光的透过率，在三种典型激光波长中，由于1.06 μm激光的散射和吸收特性都比较小，因此1.06 μm激光入射的直接衰减最小，透过率最大。

(4)激光通过卷云的透过率与卷云的散射模型、卷云的光学厚度、冰晶粒子的有效半径等因素有关，由于真实大气环境中云相态是复杂多变的，故需建立精确的云模型来求解激光在有云大气的辐射传输特性。

本工作为星地链路激光在球形边界云层的传输特性提供参考依据，并且可以推广到水云、冰水混合云和气溶胶等其他复杂相态大气背景下的激光辐射传输问题。