大学物理实验成绩影响因素的多层线性分析

钟志强,高 红

(鞍山师范学院 物理科学与技术学院,辽宁 鞍山 114007)

在教育研究中，对影响学生学习成绩的分析，不仅要考虑个人因素，如性别、兴趣爱好、智商高低、入学分数等，还要考虑他所处的学校或班级的环境因素，如学校或班级风气、教师资历、教学设施等，学生个人层面因素与学校或班级层面因素之间的相互作用值得分析和研究[1].多层线性模型(Hierarchical Linear Modeling,HLM)或多水平模型(Multilevel Modeling,MLM)将数据分层处理：处于第一层的观察因素是学生信息变量，第二层的观察因素是班级信息变量.用第一层回归方程的每个自变量的截距和斜率分别作为因变量，把第二层级的变量作为自变量，再建立回归方程，即“回归的回归”[2].用多层线性模型研究具体教育问题包括两个方面:一是不同班级学业成绩之间是否存在差异，哪些因素会对班级学业成绩产生显著影响;二是不同学生个体间学业成绩是否存在差异，哪些因素会对学生学业成绩产生显著影响[3].

本次研究建模与分析工具利用的是Mplus 7.4，主要通过代码语句完成结构模型,是综合多个潜变量模型于一体的分析框架.利用该软件分别建立多层线性模型，借此研究影响大学物理实验成绩的教师因素和学生因素.

1 研究数据

1.1 数据来源

辽宁省电子信息产业校企联盟是由省内33所高校和36家电子信息行业的科研院所及企业组成.以联盟内高校教师微信群作为联系渠道，通过某问卷网站对大学物理实验师资和授课情况在线填答并进行数据汇总.

大学物理实验课程是电子信息类大学生知识体系的重要基础，主要包括基本误差理论、基本仪器使用、力学实验、电学实验和光学实验等内容，普遍采用刘汉臣等编的《大学物理实验》或杨述武等主编的《普通物理实验(1-3)》教材，其教学内容具有普遍稳定性.调查的学校基本开设了如下教学实验：拉伸法测钢丝的弹性模量(y1)、三线摆(y2)、惯性秤(y3)、伏安法测量电阻(y4)、用惠斯通电桥测电阻(y5)、用牛顿环测定透镜曲率半径(y6).评分标准基本一致：每个实验报告成绩以10分制进行评定，其中，预习2分，实验操作4分，结果报告4分，将上述开设的6个实验汇总得出实验成绩(STUSCORE).

此外，调查项目还包括：(1)学生层面信息：高考物理成绩(STUPHYSICS)、是否通过微课预习实验题目(STUPRE)(1是，0否)、教师对实验报告的评语反馈给学生的帮助程度(STUFK)(采用李克特5级量表：5非常有帮助、4有些帮助、3不确定有帮助、2没有太多帮助、1没有任何帮助)、学生的性别(STUGENDER)(1男，0女)；(2)教师层面信息：教师的学历(TEAEDU)(3博士、2硕士、1本科)、教师的职称(TEAGRADE)(4教授、3副教授、2讲师、1助教)、教师的教学经验(TEAAGE)(以年为单位计算)、教师教学投入(TEAINPUT)(平均每次实验的备课、器材准备和批改实验的时间，5代表4 h以上、4代表3～4 h、3代表2～3 h、2代表1～2 h、1代表1 h以内).

1.2 多层线性模型数据描述

自愿参与统计的大学物理实验课程教师50人，每个教师提供其已完成教学任务班级的20～30个学生数据，总计得到自愿参加问卷调查的1 215名学生数据.预先已告知学生填报数据仅为教学科研使用，不会对其学习评价产生任何影响，希望学生如实作答.由于教师或学校(班级)的差异对学生的成绩会有影响，因而，本实例中把学生实验成绩分解为由学生差异造成的部分和由学校(班级)教师差异造成的部分，并且符合多层采样研究要求[4]，当组数为50、各组大小在20左右就能达到多层线性模型统计方法数据量的要求.统计的基本信息详见表1，其中，学生实验成绩(STUSCORE)、高考物理成绩(STUPHYSICS)的峰度与偏度都在0附近，属于正态分布，满足后期多层线性数据分析理论要求.

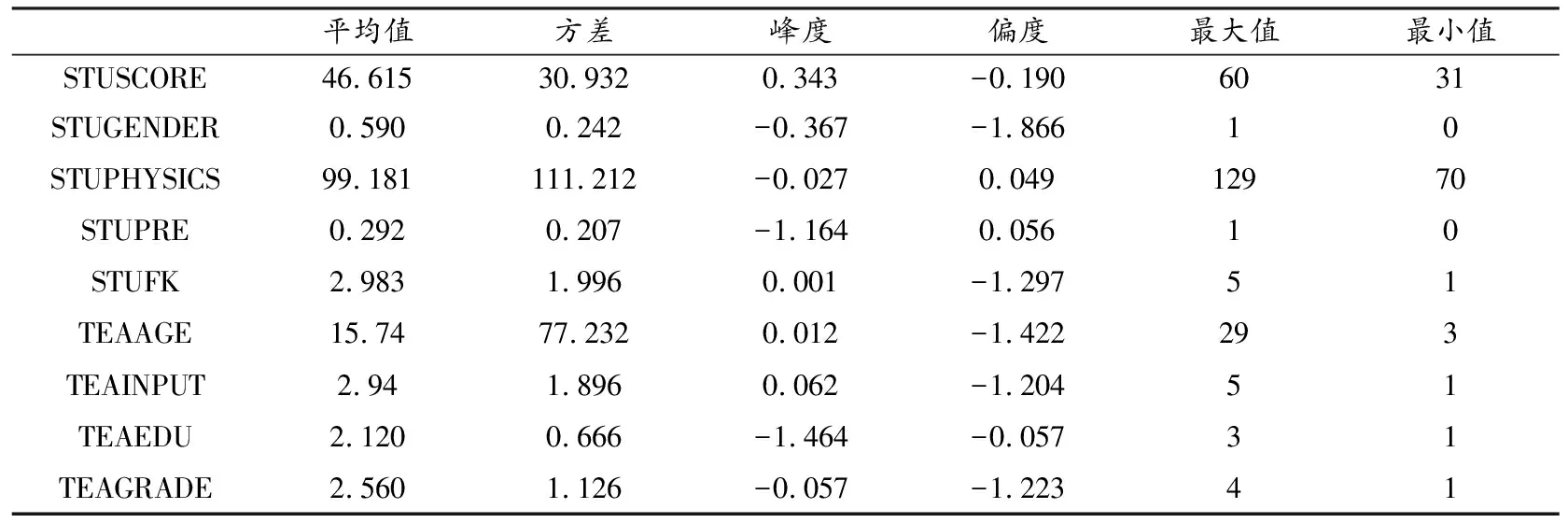
表1 影响大学物理实验成绩因素数据统计表

1.3 形成性评价数据描述

在前期的统计数据源基础上，整理出完整提供6个实验成绩与反馈信息的数据作为形成性评价数据，涉及的样本数为430人，数据描述统计见表2.

表2 6次大学物理实验成绩及相关数据统计表

从表2可知，6次实验平均成绩都在8分左右，方差相对平均值分散程度不大,峰度与偏度在0附近；高考物理平均成绩(SCORE)约98分，成绩峰度与偏度均在0值左右，说明这几项样本数据基本正态分布，符合后期数据追踪分析理论假设需求；实验报告批改反馈(FK平均约3分：不确定有帮助)，意味着较多数量的学生基本不看教师批改，或教师没有落实有效的批改反馈；实验前有24.4%的学生利用微课(VK)进行预习，说明微课没有形成主流学习方式.

由于全体学生成绩数据样本变化图难以分辨，为了便于观测个体发展趋势，随机抽取10名学生观测其6次成绩变化，如图1所示.为了不失整体研究效果，将被调查的学校分成3组：985与211学校组(88名样本)、普通大学组(201名样本)、师范院校组(141名样本)，3组学生实验成绩平均发展情况如图2.

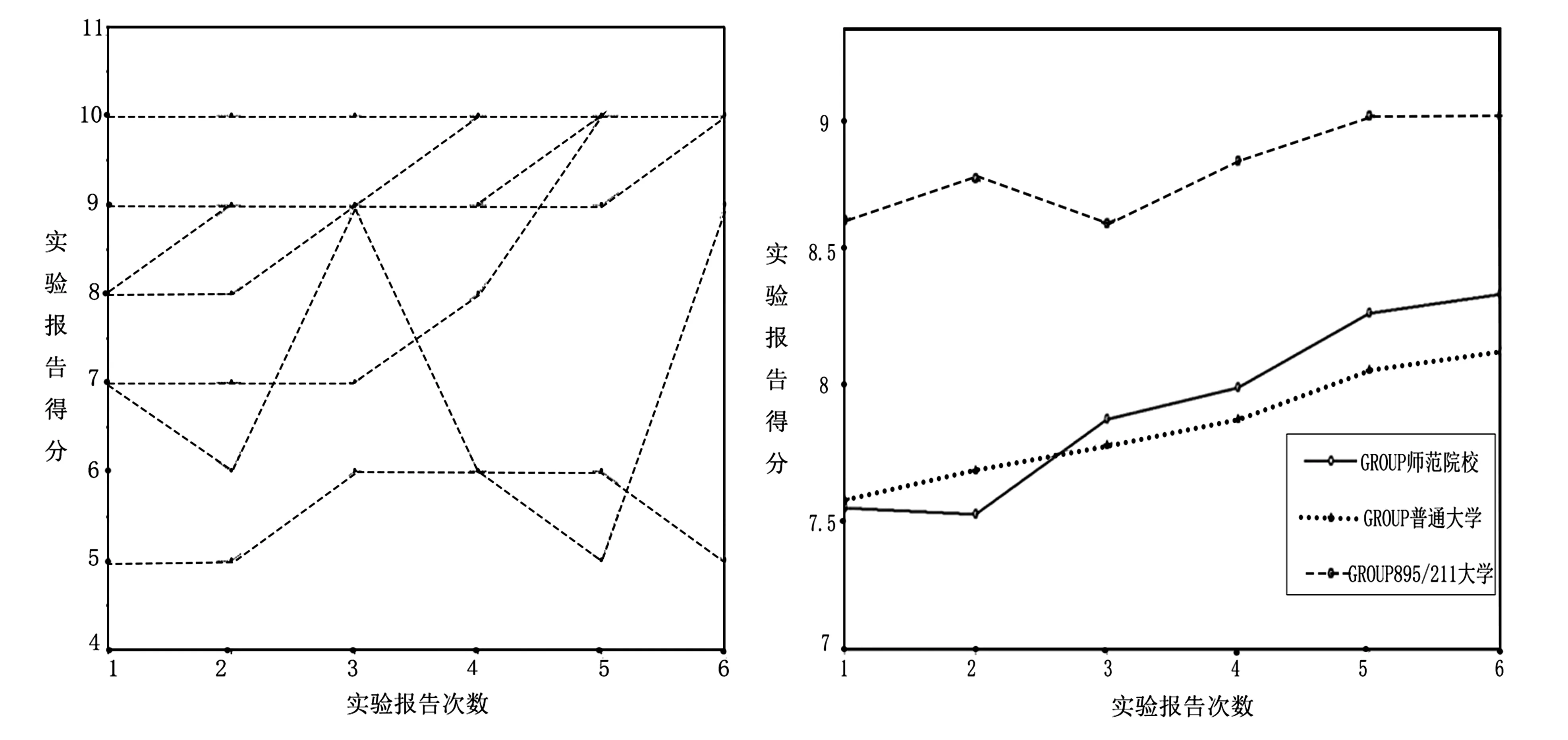
图1 随机10人样本6次实验成绩变化图 图2 3组学生实验成绩平均值追踪变化图

从图1可知，由于记录分数为离散方式，所以10人的发展趋势为折线图.其中,部分个体发展折线有重合，表现出5个起点3个终点折线，多数样本发展趋势平稳，个别样本成绩有波动，基本属于线性发展.由此推论出总体发展情况也应如此，这是满足后文追踪数据的线性模型选择的前提条件.

从图2可知，重复测量数据具有线性发展趋势，数据组间有区别，具有异质性.其实际意义是：群组实验成绩发展总体稳中微涨；985与211学校组学生实验平均成绩总体高于普通大学和师范院校学生实验平均成绩，差距相对明显；实验平均成绩起点(截距)师范院校低于普通大学；实验平均成绩发展速度(斜率)师范院校略高于普通大学.此结论是分层模型选择的前提，并会在后面的分析中继续加以说明.

由于教师对学生成绩的评价不会像统一考试那样相对客观标准，具有一定主观性，但其评价参考了基本一致评分标准，并且在每个实验总分值不大(10分)、评分成绩分散程度较小的前提下，主观评价的个体偏差可以认为在测量误差允许范围内，并且在数据量较大的情况下，其总体数据仍不失客观依据.

2 基于多层线性模型的教师因素和学生因素影响效果分析

2.1 学生—教师二层模型的建立

假设第一层次为学生,第二层次为教师(以教师所在班级为考察对象).第一层次模型与传统的回归模型类似,第二层次回归方程的截距和斜率不再假设为一个常数,而是不同班级的学生回归方程的截距和斜率,是一个随机变量.各班学生回归方程的截距和斜率都直线依赖于第二层次变量(如教师的教学经验),这样就构成了学生—教师二层模型.参考相关研究[5-6]，模型如下:

第一层学生:Yij=β0j+β1j×Xij+eij；

第二层教师:β0j=γ00+γ01×Wj+u0j，β1j=γ10+γ11×Wj+u1j.

合并的模型表示为:

Yij=γ00+γ10×Xij+γ01×Wj+γ11×Xij×Wj+u0j+u1j×Xij+eij，

其要求：

E(eij)=0,

var(eij)=σ2，

cov(u0j,rij)=cov(u1j,rij)=0，

E(β0j)=γ00,var(β0j)=var(u0j)=τ00;

E(β1j)=γ10,var(β1j)=var(u1j)=τ11;

cov(β0j,β1j)=τ01=τ10.

上述公式中，下标i代表的是第一层的个体(学生)，下标j代表的是第一层的个体(学生)所隶属的第二层的单位(教师主导的班级)；结果变量Yij(Outcome variables)表示第j个单位中的第i个个体的因变量值,本实例中具体是指Yij代表第j班级第i位学生的大学物理实验成绩；预测(解释)变量Xij(Predictors variables)表示第j个班级的第i个学生的某一个变量观测值(如:学生入学物理成绩)；β0j是第一层的随机截距，第j个单位的平均数，即代表了第二层单位的各组平均值；β1j是第一层的随机斜率；ei表示第一层的随机误差项(残差residual)，表示未被当前自变量解释的残差变异，不能被自变量所解释的部分.

第二层教师某个预测变量j表示第j个班级的教师某一个特征变量(如教师的教学经验)；γ00是第二层回归直线的截距，即全部第二层的平均水平，这里是各班级平均成绩的平均数，就是随机截距的总平均数；γ11为第二层回归直线的斜率；u0j表示第二层上的随机误差项(残差)，是截距的变异数，即第j个教师某个特征变量带来的截距上的误差；γ10,γ11分别表示截距β1j对于教师某个情境变量j的回归直线的截距和斜率；u1j表示由第j个教师特征变量带来的斜率上的误差；τ00是全体学生成绩的总方差，τ11是各班学生成绩斜率的总方差，τ01和τ10是斜率和截距间的总体协方差.

2.2 模型分析过程

2.2.1 模型一：随机效应单因数方差分析 随机效应单因数方差分析模型(one-way ANOVA with random effects)，又称空(零)模型(NULL Model).多层线性模型分析首先建立空模型，空模型各层方程中都不包含预测变量(自变量).空模型建立的目的是通过判断第二层级的数据是否对因变量Y产生了显著影响.其表示如下：

第一层:Yij=β0j+eij；

第二层:β0j=γ00+u0j；

合并的模型表示为:Yij=γ00+u0j+eij.

总体Y的变异(方差)是由个体差异的组内方差(Within variance)和教师层差异的组间方差(Between variance)共同造成的.组内方差Var(eij)=σ2，组间方差Var(μ0j)=τ00，总方差var(Yij)=var(γ00+μ0j+eij)=σ2+τ00，要求层一、二的随机误差不相关，即cov(eij,μ0j)=0.结果变量方差的组内相关系数ICC(Intra-class Correlation Coefficient)的值：ρ=τ00/(σ2+τ00).其计算的是教师层差异在总体变异中占的比例,并以此判断所选取的样本数据是否适合采用分层分析方法.

运用多层线性模型分析数据的前提条件是因变量的组间差异必须显著，如果没有产生显著影响，说明只需采用多元回归进行统计分析就可以；反之，表明班级和班级之间的变量差异较大，需要使用多层线性分析模型.

本实例中，第一层学生层面和第二层教师层面都没有预测变量或自变量的模型，可以得到随机效应的一元(单因数)方差模型.其结果组内方差σ2=7.377，组间方差τ00=14.354，ρ=0.556.说明大学物理实验成绩的总变异中55.6%是由班级层面变异造成的，其余的变异由学生个体差异来解释.根据对ICC的判断标准：在0.01～0.059之间为低关联，在0.059～0.138之间为中等关联，大于0.138时为高关联.本研究的ICC值属于高关联，即大学物理实验成绩在班级之间存在显著差异，有必要进行二层模型分析以确定变异的成分，对组间变异进行进一步解释.

2.2.2 模型二：截距与斜率回归模型 确定二层模型分析(模型一的任务)以确定变异的成分后，需要遴选在两个层面同时确定影响结果变量的因素.基本模型考虑的首要问题是精确凝练、方便理解，因此使用一个解释变量，而在实际运用中需要多个变量同时考虑，每个变量单独调用，操作起来费时费力.由于Mplus功能强大和操作灵活，合并两层各自检验因数载荷显著性步骤(HLM软件分析遵守的原则)，即将随机系数回归模型和以均值为结果的回归模型合并到截距与斜率回归模型中进行分析.一次性分析两个层面中多个变量是否符合拟合指标，参考相关研究[7]，其模型表示为：

……

以上符号和下标的意义同基本模型.其包含了第一层的预测变量和第二层的预测变量，通过完整模型，可以深入地解释因变量Y的总体变异是如何受第一层与第二层的变量影响.

相对基本模型第一层由一个变量观测值扩展了多个预测变量Xpij(p=1,2…)，其回归系数β0j从随机截距扩展到βpj(p=1,2…)随机斜率，随机斜率代表第二层单位之间的变异；γ00从随机截距的总平均数纵向扩展γp0(p=1,2…)，为各组随机斜率的截距(斜率的平均数)，γp0(p=0,1,2…)是固定效应.第二层由一个变量观测值扩展了多个Wqj(q=1,2,3…)，γ00从随机截距的总平均数横向扩展到γ0q(q=1,2,..)随机截距的斜率.如此整个γpq成为重要的分析对象，是固定效应.随机误差项(残差)upj(p=0,1,2,..)是斜率的变异数，是随机效应，是与传统协方差分析的不同之处.相对基本模型，其模型要求进一步扩展：

eij～N(0,σ2),

cov(uoj,eij)=…=cov(upj,eij)=0,

cov(uij1,uij2)=0,j1≠j2.

将调查的变量都代入模型中，计算结果见表3.

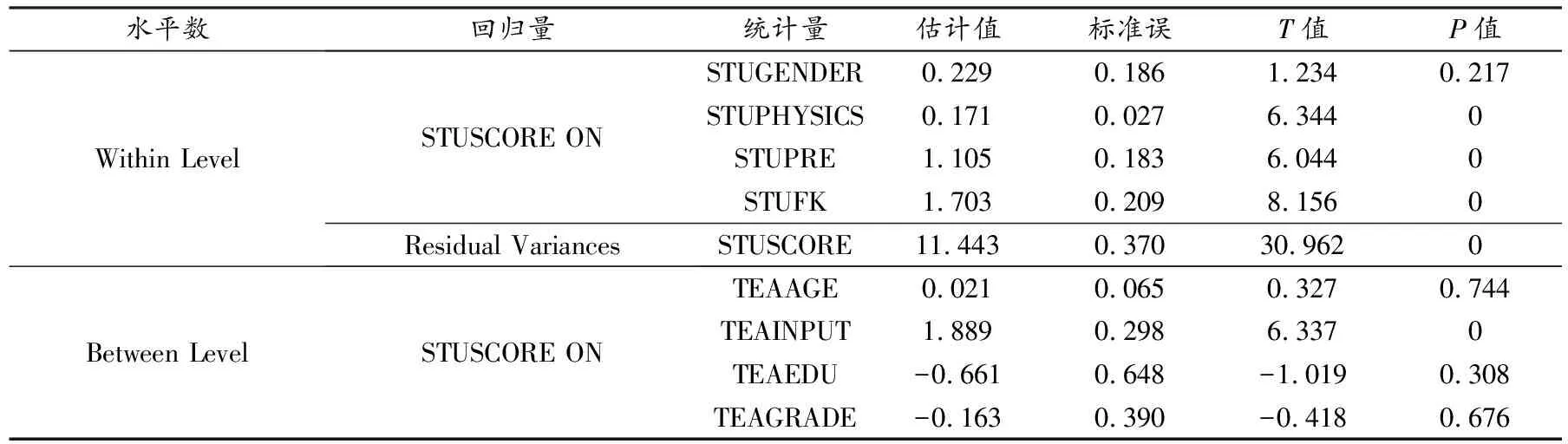
表3 截距与斜率完整模型回归系数计算结果

从表3可知，在第一层学生影响因素中，性别(STUGENDER)因素与物理实验成绩(STUSCORE)之间没有显著相关(P=0.217),入学物理成绩(STUPHYSICS)与实验成绩显著相关(P<0.05)，但作用较小(载荷因子0.171),学生的预习(STUPRE)与实验成绩显著相关(P<0.00,载荷因子1.105),学生反馈的利用(STUFK)与实验成绩显著相关(P<0.00,载荷因子1.703);在第二层教师影响因素中,教师经验(教龄TEAAGE)、学历(TEAEDU)、职称因素(TEAGRADE)与物理实验成绩之间没有显著相关(P>0.05)，教学投入与实验成绩显著相关(P<0.00)且作用较大(载荷因子大于1.889)，表示教师每增加1 h的工作投入(1～5 h的统计区间)，学生的物理实验成绩会有1.889分的增加.为此，将学生性别(STUGENDER)、入学物理成绩(STUPHYSICS)、教师教学经验(教龄TEAAGE)、学历(TEAEDU)与职称因素(TEAGRADE)移出模型，重新建立模型，其计算结果见表4.可知留下的因素均达到显著水平.

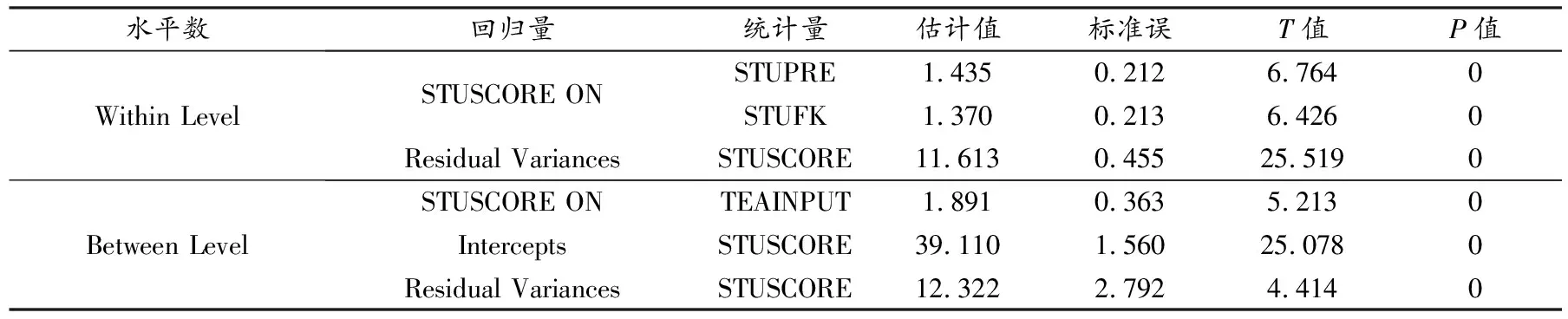
表4 修订截距与斜率回归模型回归系数计算结果

2.2.3 模型三：跨水平交互作用模型 研究跨水平交互作用(Cross-level Interactions)是多层线性分析的又一个重要问题.如果水平一解释(预测)变量(Xij)对结果变量(Yij)在各组之间有显著差异，则需分析情境变量(Wj)会影响水平一预测(Xij)与结果变量(Yij)的关系.如果水平二情境变量(Wj)对水平一斜率系数(β1j)效应统计显著，表明结果水平一变量(Yij)和预测(Xij)的关系取决于水平二情境变量(Wj)影响与调节[8].

为了计算调节效果，需要将预测变量进行组均值的中心化，以减少变量之间的共线性.中心化有两种方式：总均值中心化(Grand-mean Centering)和组均值中心化(Group-mean Centering).经过中心化处理，变量的测量值变成了相对值，代表某个个体在群组的相对位置.当引入变量的取值为零且截距意义不清楚时，也可以对其中心化[9].

通过模型二截距与斜率回归模型,确定了参与模型分析两个(水平)层的参与变量，其中，假设教师的投入与学生反馈的运用可能有跨水平交互作用，由于对斜率的计算就是估计交互作用的调节效果，故而需要用TEAINPUT与STUFK相乘，如果斜率差异显著，说明存在调节效果.将学生的预习和反馈进行了组均值中心化，教师的投入进行了总均值中心化，因而跨水平交互作用模型的表达(直接代入预测变量)方式如下：

第一层学生:

Yij=β0j+β1j×STUPRE+β2j×STUFK+eij；

第二层教师:

β0j=γ00+γ01×TEAINPUT+u0j，

β1j=γ10+u1j，

β2j=γ20+γ21×STUFK+u2j.

模型拟合指标计算结果见表5.从表5可知，S1(P=0.882)、S2(P=0.942)统计意义不显著，说明第一层内交互作用不强，并且预习与利用反馈二者相互关系不紧密，即大多数学生没有同时兼顾预习和反馈两个环节.跨水平交互作用中，学习成绩(STUSCORE)与教师投入(TEAINOUT)回归系数是1.924，且统计意义显著(P<0.05)，这与前面模型二的统计意义基本一致.这也说明只要教师投入大，各个班级的学生都有成绩提高的可能.

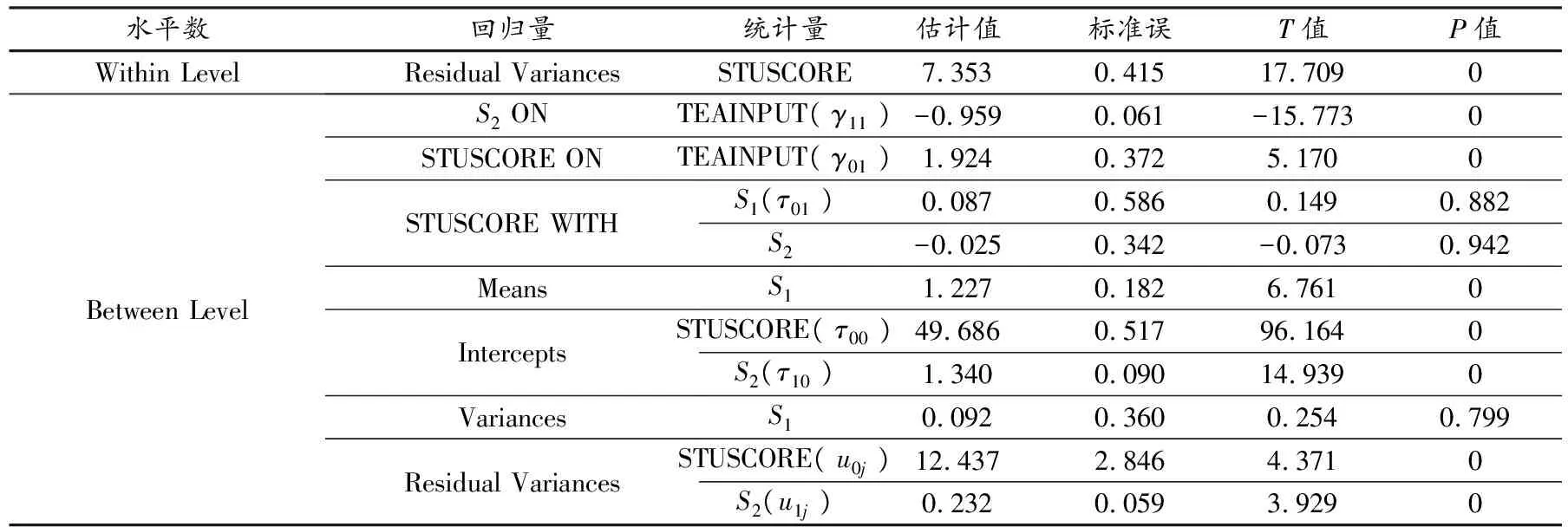
表5 跨水平交互作用模型回归系数计算结果

学生的反馈(STUFK)跨层与教师投入(TEAINPUT)负相关(-0.959)，且统计意义显著(P<0.05)，说明如果学生能够更多地利用反馈信息，教师可以在较小的投入量下使学生获得相同的成绩，这也说明教师投入具有跨层交互作用.

2.2.4 最终模型的确定 根据文献[7],多层线性模型研究各模型的关系和分析一般按顺序要求(Bottom-up从简单到复杂),先构建仅有斜率的常数项模型，再添加低水平预测变量，然后添加高水平预测变量，最后加入随机效应和跨层交互变量.

将模型一、二、三运行结果部分内容汇总得到表6，以便对比分析.从表6可知AIC、BIC数值在减小，表明模型拟合在提高.以模型二作为基准，检查引入跨模型交互分析后确立模型三.使用逆向S&B法[10],公式为:

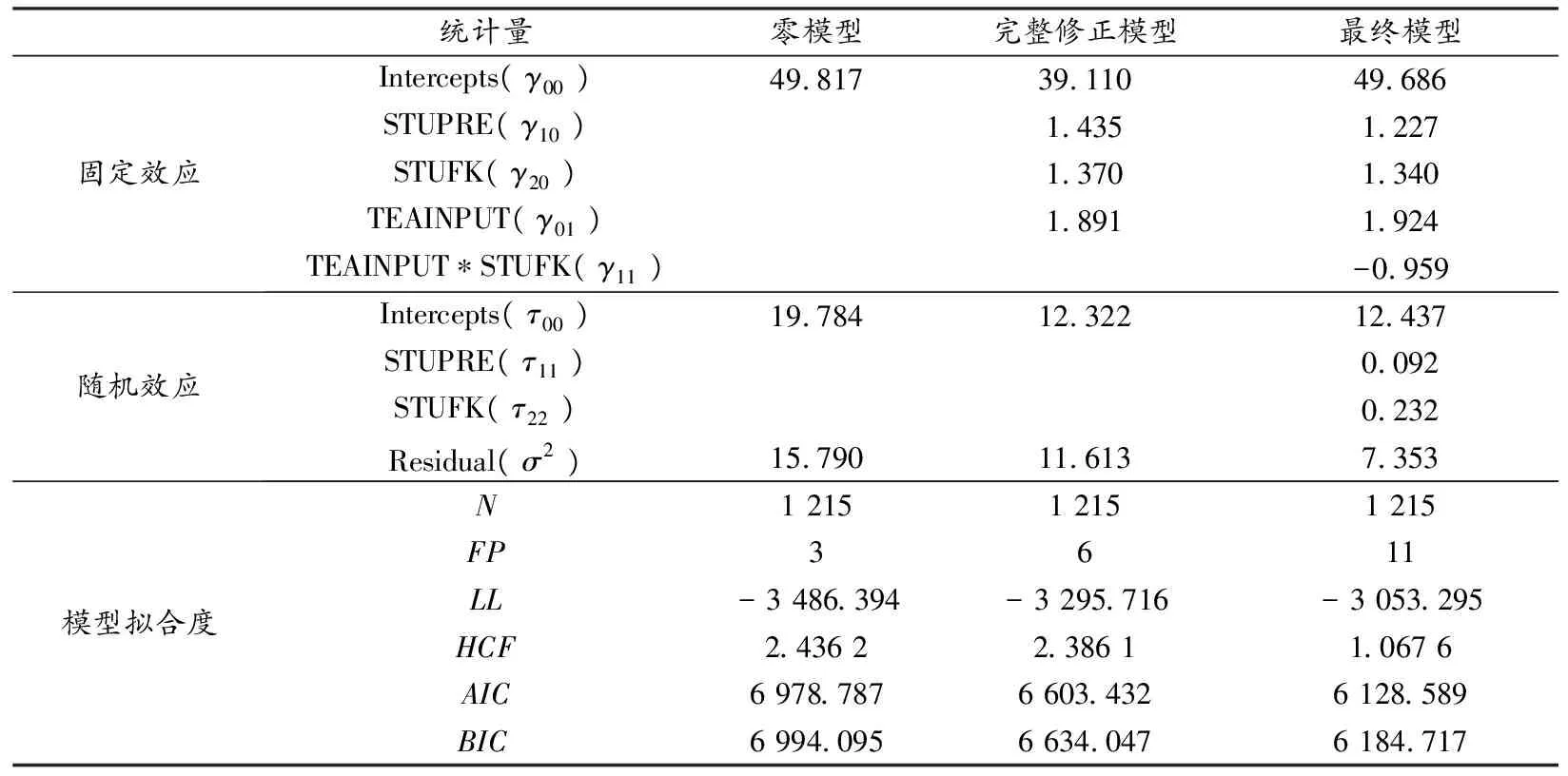
表6 物理实验成绩多水平回归分析各模型计算结果

可知，相对模型二,模型三改进已经不大，解释力没有变化，从理论上说明没有再次改进的必要.把模型三作为最终模型解释实际状况，并以此解释模型意义.

固定效果(Fixed effect) 对应模型中的变量γ，表现为截距或斜率的平均值，其参数具有跨群组的不变性[11].随机效果(Random effect)对应模型中的变量u，是表现在固定效果上的随机变异状况，即截距或斜率的方差，其参数会随群组变化[12].

表6中数据均达到显著水平，从中可知:γ00(49.686)说明总平均分数是50分，是截距的平均数；γ01(1.924)为平均斜率,其意义如前文所述；γ10(1.227)和γ20(1.340)分别是第一层回归直线中自变量学生预习和学生反馈回归直线的斜率；反馈的分散效应τ22(0.232)大于预习的分散效应τ11(0.092)，说明学生对反馈利用程度不同，对教师提出的改进方法不明了，教师反馈还有很大的教改空间，学生对教学反馈的利用程度对各层级教学成绩有较大的影响.

3 小结

大学物理实验成绩在班级之间存在显著差异.在第一层学生影响因素中，入学物理成绩、学生的预习和学生反馈的利用与实验成绩显著相关；在第二层教师影响因素中，教学投入与实验成绩显著相关且作用较大，教师投入具有跨层交互作用，教师反馈对学生实验成绩有影响且组间差异性较大，具有调节作用.