一次数学探究之旅
——记一道几何证题的推广
上海市华东政法大学附属中学(200052) 许 超
例在ΔABC中,AB=AC,O为ΔABC内一点,∠A=80°,∠OBC=10°,∠OCB=20°,求∠CAO的度数.
分析很容易发现∠ACO= 30°,因此我们从这个角出发,将ΔBCO绕点C旋转60°,于是就构造出了一个等边ΔOCO′.
证明:将ΔBCO绕点C顺时针旋转60°,连结OO′,BO′,易知ΔOCO′为等边三角形,则OC=OO′.在ΔBOC中,∠BOC= 180° -10° -20°= 150°,而∠BOO′= 360° -60° -150°= 150°= ∠BOC,易得ΔBOC∽= ΔBOO′,可知∠CBO′= 20°,∠BO′O=∠BCO= 20°,则∠AOO′= ∠ACB= 50°,则点A、B、C、O′四点共圆,则∠CAO′= ∠CBO′= 20°,易得ΔCAO′∽= ΔCAO,则有∠CAO=∠CAO′=20°.
回顾与反思:解完之后细细品味,如果点O的位置发生变化,如果点O不在ΔABC内,又会发生怎样的变化呢?


推广1在等边ΔABC中,∠OBC= 10°,∠OCB=20°,求∠CAO.
分析此时点O处于ΔABC内,观察这个图形,我们不妨将ΔBCO绕点C顺时针旋转60°,于是就构造出一个等边三角形.
证明将ΔBCO绕点C顺时针旋转60°,连接OO′,∠ACO′= 60° -40°= 20°= ∠BCO,则ΔBCO∽= ΔACO′,则∠O′AC= ∠OBC= 10°,在ΔAO′C中,∠AO′C= 180° -10° -20°= 150°,而∠AO′O= 360° -60° -150°= 150°= ∠AO′C,易得ΔAO′C∽= ΔAO′O,则∠OAO′= ∠CAO′= 10°,则∠OAC=10°+10°=20°.
回顾与反思:当我们推广了点的位置以后,很容易就能想到若是外面的图形不是一个三角形呢,会发生怎样的变化呢?
推广2在正方形ABCD中,∠OBC= 15°,∠OCB=15°,求∠CDO.
分析:将ΔAOB绕BO中点顺时针旋转180°,ΔDOC也是如此,于是构造出了一个等边ΔBCO′.
证明作以上变换,易得四边形ABO′O与四边形DCO′O为平行四边形,则AO=BO′,DO=CO′,又BO′=CO′=BC,则AO=DO=AD,则ΔAOD是一个等边三角形,则∠CDO=90°-60°=30°
回顾与反思:当我们把等边三角形推广到正方形后,很自然地就能联想到是否还能继续推广到正五边形呢?


推广3在正五边形ABCDE中,∠OBC=6°,∠OBC=24°,求∠CDO.
分析:此题中∠OBC与∠OCB的度数均不太常见,但是如果我们注意到正五边形单个角的度数和∠OCB的度数就不难发现其中的奥秘.
证明:以OC为边构造等边三角形OCO′,连接DO′,∠O′CD= 108° -60° -24°= 24°,而∠OCB= 24°,则∠OCB= ∠O′CD,于是易证ΔOCB∽=O′CD,则∠O′DC= ∠OBC= 6°.在ΔO′DC中,∠DO′C= 180°-24°-6°= 150°,而∠DO′O= 360°-60°-150°= 150°,于是∠DO′O= ∠DO′C,于是ΔDO′O∽= ΔDO′C,则∠CDO=12°.
回顾与反思:当我们推广到正五边形之后,很容易的又能产生联想,那我能否把他推广到n边形呢?
推广4在正n(3<n <6,n ∈N)边形A1A2···An中,∠OA3A2=求∠OA4A3.
分析:此题难度较大,但是细细分析其角度便不难发现“构造等边三角形”的方法,便很容易解决.
证明以OA3为边构造等边三角形OA3O′,连接O′A4,∠A4A3O′=又∠OA3A2=则∠A4A3O′= ∠OA3A2,易证,ΔOA3A2∽= ΔO′A3A4,则∠A3A4O′= ∠A3A2O=在ΔA4A3O′中,∠A3O′A4=π -而∠OO′A4= 2π-也就是∠OO′A4= ∠A3O′A4,易得ΔOO′A4∽= ΔA3O′A4,则∠OA4A3=2∠OA2A3=
回顾与反思:推广到n边形后,由于∠OA2A3的限制,所以我们只能讨论3<n <6 的一般情况,但是我们却得到了一个十分漂亮而又美丽的结论.此时若我们回过头来再来看这个题目,ΔABC中OA、OB、OC三条边长是否具有一定的数量关系,如果知道了这三条边的长度,我们又能推得什么呢?


推广5在正ΔABC中,点O为ΔABC内任意一点,OA=a,OB=b,OC=c,求正ΔABC的边长.
分析:通过旋转将这几条边转化到一个图形中,之后采用“面积法”辅助.
证明将ΔACO绕点C旋转60°,连接OO′.易证,ΔAOC∽= ΔBO′C,则BO′=AO=a,根据海伦公式,有此时

同理,

回顾与反思:当证明到这个结论之后,下一个很自然的猜想就是这个结论能否推广到正方形中?
推广6在正方形ABCD中,点O为正方形ABCD内任意一点,OA=a,OB=b,OC=c,OD=d,求正方形ABCD的边长.
分析基本方法不变,我们依旧尝试把这几条边转化到一起.
证明:将ΔABO逆时针旋转90°,使 点B至点D,点O至 点O′.ΔABO∽= ΔADO′,OB=O′D=b,O′A=OA=a,OO′=则其中P1=令SΔO′OD=S1,则

同理,

其中S3=

其中S4=P4=

回顾与反思:当我们在正方形中依然推得这个结论后,就自然而然地想到能否在正n边形中依然能够推得这个结论?a2,··· ,OAn=an,求正n边形A1A2···An的边长.


分析基本方法依旧不变,还是把这几条边转化到三角形中.
证明将ΔOA1A2顺时针旋转
推广7在正n边形A1A2···An中,OA1=a1,OA2=使点O至点O′,点A1至点A3.易知,ΔOA1A2∽= ΔO′A2A3,O′A2=OA2=a2,O′A3=OA1=a1,在等腰ΔO′A2O中,∠A2O′O=,A2H1=a2sin ∠A2O′O=O′O=2O′H1=
其中P1=则
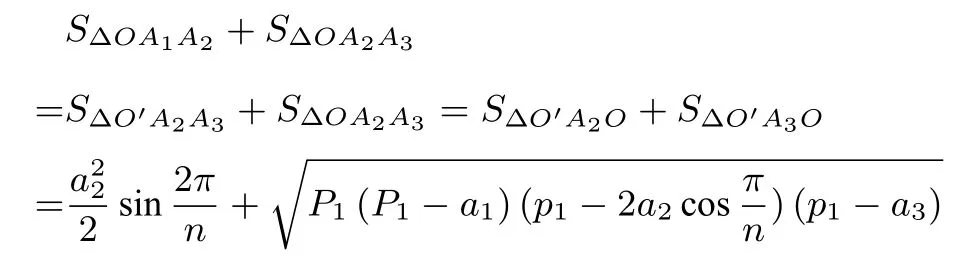
一般地,Ak+1Hk=则

其中Pk=进行累加,

此时再从另一个角度计算正n边形的面积,作出正n边形的中心点O′′,连接O′′A1,O′′A2,··· ,O′′An,设正n边形边长为x,则SA1A2···An=nSΔO′′A1A2=
在此次数学之旅中,我们通过不断变换点的位置与图形的形状,不断的发现一个又一个美妙的结论.通过此次探究,希望能给几何的学习提供一个方向,并且能够从中获得别样

